1.2.2 单位圆与三角函数线 课件(共26张PPT)2020-2021学年高中数学人教B版必修4
文档属性
| 名称 | 1.2.2 单位圆与三角函数线 课件(共26张PPT)2020-2021学年高中数学人教B版必修4 |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-01 09:33:44 | ||
图片预览







文档简介
(共26张PPT)
普通高中课程标准实验教科书人教B版
《单位圆与三角函数线》
2
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
三角函数
3
单位圆与三角函数线
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
-
-
-1
1
-
4
你还记得这些知识吗?
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
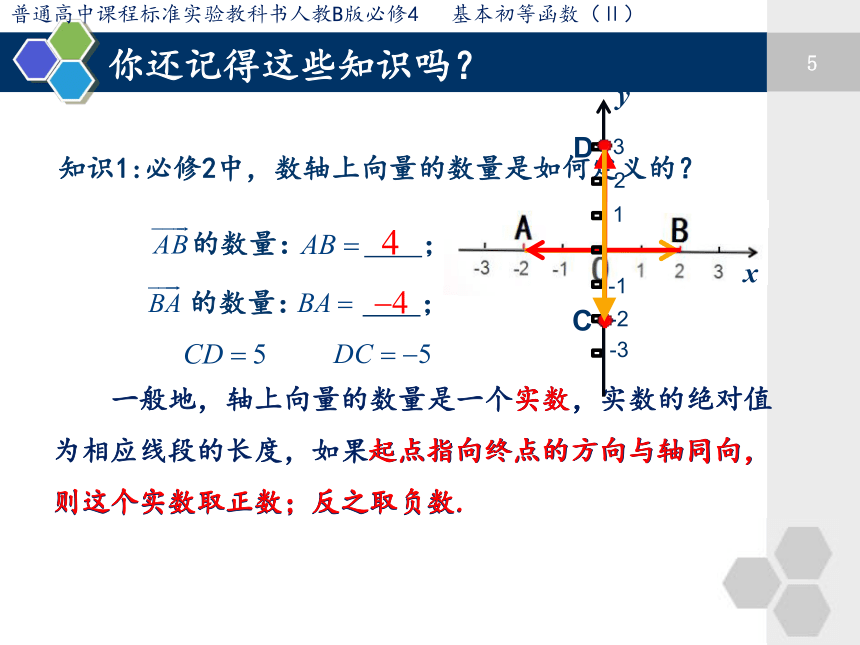
知识1:必修2中,数轴上向量的数量是如何定义的?
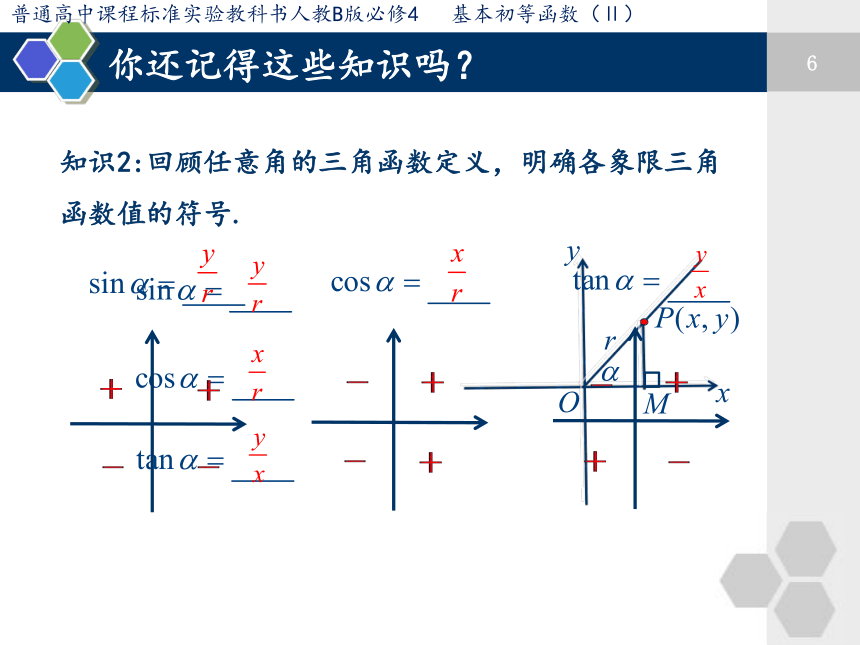
知识2:回顾任意角的三角函数定义,明确各象限三角
函数值的符号.
知识3:在三角函数的定义中,若
,则点
的集合
是何图形?
D
5
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
你还记得这些知识吗?
知识1:必修2中,数轴上向量的数量是如何定义的?
一般地,轴上向量的数量是一个实数,实数的绝对值为相应线段的长度,如果起点指向终点的方向与轴同向,则这个实数取正数;反之取负数.
则这个实数取正数;反之取负数.
实数,
起点指向终点的方向与轴同向,
的数量:
;
的数量:
;
-3
y
-2
-1
1
2
3
x
C
6
你还记得这些知识吗?
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
知识2:回顾任意角的三角函数定义,明确各象限三角
函数值的符号.
7
你还记得这些知识吗?
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
知识3:当
时,任意角
终边上点
的集合是何图形?
8
概念形成
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
一般地,我们把半径为1的圆叫做单位圆.
注意:(1)半径为1(其中1表示一个单位长度);
(2)为了研究的方便我们把圆心定位在坐标原点.
过点
作
垂直
轴于
,则
就是点
在
轴上的正射影.
9
互动探究
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
探究一:正弦线、余弦线
问题1:结合单位圆和三角函数的定义,你能否用角
的正、余弦来表示点
的坐标?
角
的余弦和正弦分别等于角
终边与单位圆交点的横坐标和纵坐标.
10
互动探究
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
探究一:正弦线、余弦线
问题2:当角
的终边落在不同象限时,点
坐标中,
与
,
与
有何关系?
11
概念形成
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
正弦线、余弦线
如图所示,与单位圆有关的有向线段(轴上向量)
分别叫做角
的正弦线、余弦线.
有向线段(轴上向量)
12
学以致用
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
练习一:分别作出下列各角的正弦线、余弦线:
(1)
(2)
总结:
作正弦线、余弦线的步骤:
(1)在坐标系中,做角
的终边与单位圆交点
;
(2)过点
做
轴的垂线,设垂足为
,得正弦线
、余弦线
.
②当角
的终边在
轴上时,余弦线变成了一点,
它的数量为零,而正弦线的数量
或-1.
①当角
的终边在
轴上时,点
与点
重合,
这时正弦线变成了一点,它的数量为零,而余
弦线的数量
或-1.
13
互动探究
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
探究一:正弦线、余弦线
问题3:如果角
的终边落在坐标轴上,你能否发现其正弦线、余弦线的变化特点?
14
互动探究
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
问题1:类比正弦线、余弦线的探讨过程,如何寻找正切线呢?
探究二:正切线
提示:(1)令
,则
,从而可得出正弦线.
(2)你能否将表达式
中的分母化为1?
请同学们以终边在第一象限的情况为例来做分析.
15
互动探究
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
16
概念形成
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
如图所示,与单位圆有关的有向线段(轴上向量)
叫做角
的正切线.
有向线段(轴上向量)
17
学以致用
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
总结:
作正切线的步骤:
过点
作单位圆的切线,与角
的终边或其反向延长线的交点设为
,得角
的正切线
.
练习二:分别作出下列各角的正切线:
(1)
(2)
②当角
的终边在
轴上时,正切线不存在.
①当角
的终边在
轴上时,点
与点
重合,
这时正切线变成了一点,它的数量为零.
18
互动探究
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
探究二:正切线
问题2:如果角
的终边落在坐标轴上,你能否发现其正切线的变化特点?
19
迁移应用
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
例:比较下列各式的大小:
(1)
;(2)
;(3)
解:由三角函数线得:
sin1cos1>cos1.5
tan2注意负数比较大小的方法.
学生分组合作,运用本节知识解决下列问题:
观察角的终边在各位置的情形,结合三角函数线和已学知识,你还能发现什么规律?得出哪些结论?请说明你的观点和理由.
20
拓展研究
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
-
-
-1
1
-
21
我的收获
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
知识要点:
1
题型方法:
2
数学思想:
3
单位圆、三角函数线
(1)作任意角的三角函数线;
数形结合、转化类比
(2)三角函数线的灵活应用.
22
反馈演练
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
1、(基础题)如图所示,
是角
的终边与单位圆的交点,
轴于点
,且
和
均为单位圆的切线,则角
的(
)
正弦线为
,正切线为
正弦线为
,正切线为
正弦线为
,正切线为
正弦线为
,正切线为
23
反馈演练
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
2、(提升题)设
,
,
则有(
)
3、(拓展题)已知
,求角
的取值集合.
23
评价量规
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
同学们,你做到了吗?
数
形
结
合
小小单位圆藏乾坤
三角函数线显真容
普通高中课程标准实验教科书人教B版
《单位圆与三角函数线》
2
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
三角函数
3
单位圆与三角函数线
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
-
-
-1
1
-
4
你还记得这些知识吗?
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
知识1:必修2中,数轴上向量的数量是如何定义的?
知识2:回顾任意角的三角函数定义,明确各象限三角
函数值的符号.
知识3:在三角函数的定义中,若
,则点
的集合
是何图形?
D
5
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
你还记得这些知识吗?
知识1:必修2中,数轴上向量的数量是如何定义的?
一般地,轴上向量的数量是一个实数,实数的绝对值为相应线段的长度,如果起点指向终点的方向与轴同向,则这个实数取正数;反之取负数.
则这个实数取正数;反之取负数.
实数,
起点指向终点的方向与轴同向,
的数量:
;
的数量:
;
-3
y
-2
-1
1
2
3
x
C
6
你还记得这些知识吗?
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
知识2:回顾任意角的三角函数定义,明确各象限三角
函数值的符号.
7
你还记得这些知识吗?
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
知识3:当
时,任意角
终边上点
的集合是何图形?
8
概念形成
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
一般地,我们把半径为1的圆叫做单位圆.
注意:(1)半径为1(其中1表示一个单位长度);
(2)为了研究的方便我们把圆心定位在坐标原点.
过点
作
垂直
轴于
,则
就是点
在
轴上的正射影.
9
互动探究
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
探究一:正弦线、余弦线
问题1:结合单位圆和三角函数的定义,你能否用角
的正、余弦来表示点
的坐标?
角
的余弦和正弦分别等于角
终边与单位圆交点的横坐标和纵坐标.
10
互动探究
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
探究一:正弦线、余弦线
问题2:当角
的终边落在不同象限时,点
坐标中,
与
,
与
有何关系?
11
概念形成
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
正弦线、余弦线
如图所示,与单位圆有关的有向线段(轴上向量)
分别叫做角
的正弦线、余弦线.
有向线段(轴上向量)
12
学以致用
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
练习一:分别作出下列各角的正弦线、余弦线:
(1)
(2)
总结:
作正弦线、余弦线的步骤:
(1)在坐标系中,做角
的终边与单位圆交点
;
(2)过点
做
轴的垂线,设垂足为
,得正弦线
、余弦线
.
②当角
的终边在
轴上时,余弦线变成了一点,
它的数量为零,而正弦线的数量
或-1.
①当角
的终边在
轴上时,点
与点
重合,
这时正弦线变成了一点,它的数量为零,而余
弦线的数量
或-1.
13
互动探究
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
探究一:正弦线、余弦线
问题3:如果角
的终边落在坐标轴上,你能否发现其正弦线、余弦线的变化特点?
14
互动探究
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
问题1:类比正弦线、余弦线的探讨过程,如何寻找正切线呢?
探究二:正切线
提示:(1)令
,则
,从而可得出正弦线.
(2)你能否将表达式
中的分母化为1?
请同学们以终边在第一象限的情况为例来做分析.
15
互动探究
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
16
概念形成
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
如图所示,与单位圆有关的有向线段(轴上向量)
叫做角
的正切线.
有向线段(轴上向量)
17
学以致用
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
总结:
作正切线的步骤:
过点
作单位圆的切线,与角
的终边或其反向延长线的交点设为
,得角
的正切线
.
练习二:分别作出下列各角的正切线:
(1)
(2)
②当角
的终边在
轴上时,正切线不存在.
①当角
的终边在
轴上时,点
与点
重合,
这时正切线变成了一点,它的数量为零.
18
互动探究
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
探究二:正切线
问题2:如果角
的终边落在坐标轴上,你能否发现其正切线的变化特点?
19
迁移应用
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
例:比较下列各式的大小:
(1)
;(2)
;(3)
解:由三角函数线得:
sin1
tan2
学生分组合作,运用本节知识解决下列问题:
观察角的终边在各位置的情形,结合三角函数线和已学知识,你还能发现什么规律?得出哪些结论?请说明你的观点和理由.
20
拓展研究
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
-
-
-1
1
-
21
我的收获
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
知识要点:
1
题型方法:
2
数学思想:
3
单位圆、三角函数线
(1)作任意角的三角函数线;
数形结合、转化类比
(2)三角函数线的灵活应用.
22
反馈演练
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
1、(基础题)如图所示,
是角
的终边与单位圆的交点,
轴于点
,且
和
均为单位圆的切线,则角
的(
)
正弦线为
,正切线为
正弦线为
,正切线为
正弦线为
,正切线为
正弦线为
,正切线为
23
反馈演练
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
2、(提升题)设
,
,
则有(
)
3、(拓展题)已知
,求角
的取值集合.
23
评价量规
普通高中课程标准实验教科书人教B版必修4
基本初等函数(Ⅱ)
同学们,你做到了吗?
数
形
结
合
小小单位圆藏乾坤
三角函数线显真容
