8.3.1(用)实际问题与二元一次方程组(一)教学课件
文档属性
| 名称 | 8.3.1(用)实际问题与二元一次方程组(一)教学课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 723.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-12 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
8.3 实际问题与二元一次方程组
义务教育课程标准实验教科书 七年级 数学(下册)
8.3 实际问题与二元一次方程组
复习回顾
列方程解实际问题的步骤是什么?
审题,理清题意;
合理设未知数;
根据等量关系列方程(组);
解方程(组);
验证解是否符合实际,并作答;
8.3 实际问题与二元一次方程组
探究1
养牛场原有30只大牛和15只小
牛,1天约用饲料675kg;一周后
又购进12只大牛和5只小牛,这时
1天约需用饲料940kg。饲养员李
大叔估计每只大牛1天约需饲料18~20kg,每只小牛1天约需饲料7~8kg。你能否通过计算验证他的估计?
问题思考:
(1)题中有哪些已知量?哪些未知量?
(2)题中等量关系有哪些?
(3)如何解这个应用题?
据以往的统计资料:甲、乙两种作物的单位面积产量的比是1:1.5,现要在一块长200米,宽100米的长方形土地上种植这两种作物,怎样把这块地分为两个长方形,使甲、乙两种作物的总产量的比是3:4(结果取整数)?
100m
200m
探究2
探究2
据以往的统计资料,甲、乙两种作物的单位面积产量的比是1:1.5,现要在一块长200m,宽100m的长方形土地上种植这两种作物,怎样把这块地分为两个长方形,使甲、乙两种作物的总产量的比是3:4(结果取整数)?
分析:如图所示,一种种植方案为:甲、乙两种作物的种植区域分别为长方形AEFD
和BCFE。设AE=xm,BE=ym,根据问题中涉及长度、产量的数量关系,列方程组
,
。
解这个方程组,得
x= ,
y= ,
过长方形土地的长边离一端约 处,把这块地分为两个长方形。较大一块地种 种作物,较小一块地种 种作物。
x
y
A
B
C
D
E
F
x+y=200
100x:1.5×100y=3:4
106m
甲种
乙种
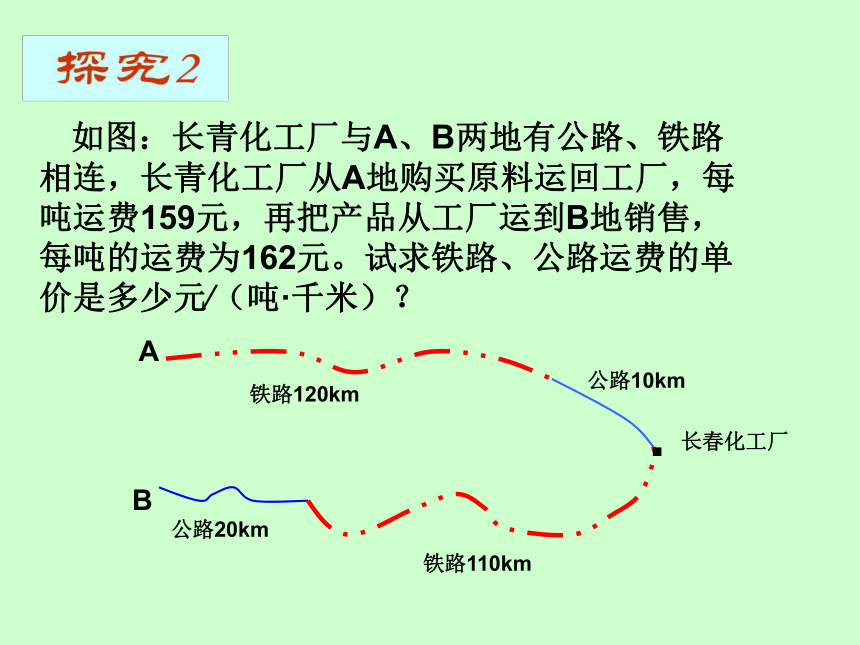
如图:长青化工厂与A、B两地有公路、铁路相连,长青化工厂从A地购买原料运回工厂,每吨运费159元,再把产品从工厂运到B地销售,每吨的运费为162元。试求铁路、公路运费的单价是多少元∕(吨·千米)?
A
B
铁路120km
公路10km
.
长春化工厂
铁路110km
公路20km
审题
2.已知的量:
3.要求的量:
1.运费的单位“元∕(吨·千米)”的含义
原料从A地运回工厂,每吨运费159元
产品从工厂运到B地,每吨运费162元
铁路、公路运费的单价
已知量与未知量的关系
原料的铁路运费+原料的公路运费=每吨原料的运费
产品的铁路运费+产品的公路运费=每吨产品的运费
解:设铁路运费为 元∕(吨·千米),公路运费为 元∕(吨·千米),依题意得:
答:铁路运费为1.2元∕(吨·千米),公路运费为1.5元∕(吨·千米)
解方程组得:
整理方程组得:
探索分析,解决问题
例题:(探究3)如图,长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地.公路运价为1. 5元(吨·千米),铁路运价为1.2元(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
A
B
铁路120km
公路10km
.
长春化工厂
铁路110km
公路20km
设问1.原料的数量与产品的数量一样多吗?
(不一样)
设问2.那些量设为未知数?
销售款与产品数量有关,原料费与原料数量有关,而公路运费和铁路运费与产品数量和原料数量都有关.因此设 .
产品 吨重,原料 吨重
设问3.如何分析题目中的数量关系?能否用列表分析?
列表分析:
产品x吨 原料y吨 合计
公路运费(元)
铁路运费(元)
价值(元)
1.5(20X)
1.2(110X)
1.5(10Y)
1.2(120Y)
1.5(20X+10Y)
1.2(110X+120Y)
8000X
1000Y
由上表可列方程组
解这个方程组,得 :
销售款为:
原料费为:
运输费为:
8000X300=2400000(元)
1000X400=400000(元)
15000+97200=112200(元)
所以销售款比原料费与运输费的和多:
2400000-(400000+112200)=1887800(元)
答:销售款比原料费与运输费的和多1887800元。
20x+40y=148
8.3 实际问题与二元一次方程组
练一练
1.买10支笔和15本笔记本需58元,买20支笔和40本笔记本需148元,问每支笔和每本笔记本各多少钱?
解:设每支笔x元,每本笔记y元。
根据题意得
10x+15y=58
解这个方程组,得
y=3.2
x=1
答:每支笔是1元,每本笔记本是3.2元
8.3 实际问题与二元一次方程组
练一练
2.有大小两种货车,2辆大车与3辆小车一次可以运货15.5吨;5辆大车与6辆小车一次可以支货35吨;3辆大车与5辆小车一次可以运货多少吨?
5x+6y=35
解:设每辆大车可运货x吨,每辆小车可运货y吨。
根据题意得
2x+3y=15.5
解这个方程组,得
y=2.5
x=4
所以,3辆大车与5辆小车一次可以运货:
3×4+5×2.5=24.5吨
8.3 实际问题与二元一次方程组
溶液问题
把浓度分别是90%与60%的甲乙两种酒精溶液,配制成浓度为75%的消毒酒精溶液500克,求甲、乙两种酒精溶液各取多少克?
分析:
1.溶液的配制过程中两种溶液的质量和是配置后溶液的质量;
2.配制过程中,纯酒精的量不变。
酒精浓度
纯酒精量
酒精溶液质量
×100%
=
8.3 实际问题与二元一次方程组
练一练
要把浓度为10%的盐水,稀释成浓度为0.9%的生理盐水100kg,需要浓度10%盐水、水各多少千克?
10%x=0.9%×100
解:设需要浓度10%的盐水xkg,水ykg。
根据题意得
x+y=100
解这个方程组,得
y=91
x=9
所以,需要浓度10%的盐水9kg,水91kg
1. 一个长方形,它的长减少4cm,宽增2cm,所得的是一个正方形,它的面积与长方形的面积相等,求原长方形的长与宽。
牛刀小试
2. 小龙在拼图时,发现8个一样大的小长
方形,恰好可以拼成一个大长方形,如图甲所示,
小明看见了说“我来试一试”,结果小明七拼八凑,
拼成一个如图乙的正方形,中间留下一个洞,恰
好是边长2mm的小正方形,你能算出小长方形
的长和宽吗?
甲
乙
牛刀小试
3. 有大小两种货车,2辆大车与3辆小车
一次可以运货15.50吨,5辆大车与6辆小
车一次可以运货35吨。
求:3辆大车与5辆小车一次可以运货
多少吨
分析:要解决这个问题的关键是求每辆
大车和每辆小车一次可运货多少吨
解决此题的
关键是什么?
牛刀小试
4.某车间有90名工人,每人每天平均能生产螺栓15个或螺帽24个,要使一个螺栓配套两个螺帽,应如何分配工人才能使螺栓和螺帽刚好配套?设生产螺栓x人,生产螺帽y人,列方程组为( )
A B、
C、 D、
c
学习致用
一船顺水航行45千米需要3小时,逆水航行65千米需要5小时,若设船在静水中的速度为x千米/小时,水流的速度为y㎞/h,则x、y的值为 ( ) A、X=3,y=2 B、x=14,y=1 C、x=15,y=1 E、x=14,y=2
B
学习致用
8.3 实际问题与二元一次方程组
义务教育课程标准实验教科书 七年级 数学(下册)
8.3 实际问题与二元一次方程组
复习回顾
列方程解实际问题的步骤是什么?
审题,理清题意;
合理设未知数;
根据等量关系列方程(组);
解方程(组);
验证解是否符合实际,并作答;
8.3 实际问题与二元一次方程组
探究1
养牛场原有30只大牛和15只小
牛,1天约用饲料675kg;一周后
又购进12只大牛和5只小牛,这时
1天约需用饲料940kg。饲养员李
大叔估计每只大牛1天约需饲料18~20kg,每只小牛1天约需饲料7~8kg。你能否通过计算验证他的估计?
问题思考:
(1)题中有哪些已知量?哪些未知量?
(2)题中等量关系有哪些?
(3)如何解这个应用题?
据以往的统计资料:甲、乙两种作物的单位面积产量的比是1:1.5,现要在一块长200米,宽100米的长方形土地上种植这两种作物,怎样把这块地分为两个长方形,使甲、乙两种作物的总产量的比是3:4(结果取整数)?
100m
200m
探究2
探究2
据以往的统计资料,甲、乙两种作物的单位面积产量的比是1:1.5,现要在一块长200m,宽100m的长方形土地上种植这两种作物,怎样把这块地分为两个长方形,使甲、乙两种作物的总产量的比是3:4(结果取整数)?
分析:如图所示,一种种植方案为:甲、乙两种作物的种植区域分别为长方形AEFD
和BCFE。设AE=xm,BE=ym,根据问题中涉及长度、产量的数量关系,列方程组
,
。
解这个方程组,得
x= ,
y= ,
过长方形土地的长边离一端约 处,把这块地分为两个长方形。较大一块地种 种作物,较小一块地种 种作物。
x
y
A
B
C
D
E
F
x+y=200
100x:1.5×100y=3:4
106m
甲种
乙种
如图:长青化工厂与A、B两地有公路、铁路相连,长青化工厂从A地购买原料运回工厂,每吨运费159元,再把产品从工厂运到B地销售,每吨的运费为162元。试求铁路、公路运费的单价是多少元∕(吨·千米)?
A
B
铁路120km
公路10km
.
长春化工厂
铁路110km
公路20km
审题
2.已知的量:
3.要求的量:
1.运费的单位“元∕(吨·千米)”的含义
原料从A地运回工厂,每吨运费159元
产品从工厂运到B地,每吨运费162元
铁路、公路运费的单价
已知量与未知量的关系
原料的铁路运费+原料的公路运费=每吨原料的运费
产品的铁路运费+产品的公路运费=每吨产品的运费
解:设铁路运费为 元∕(吨·千米),公路运费为 元∕(吨·千米),依题意得:
答:铁路运费为1.2元∕(吨·千米),公路运费为1.5元∕(吨·千米)
解方程组得:
整理方程组得:
探索分析,解决问题
例题:(探究3)如图,长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地.公路运价为1. 5元(吨·千米),铁路运价为1.2元(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
A
B
铁路120km
公路10km
.
长春化工厂
铁路110km
公路20km
设问1.原料的数量与产品的数量一样多吗?
(不一样)
设问2.那些量设为未知数?
销售款与产品数量有关,原料费与原料数量有关,而公路运费和铁路运费与产品数量和原料数量都有关.因此设 .
产品 吨重,原料 吨重
设问3.如何分析题目中的数量关系?能否用列表分析?
列表分析:
产品x吨 原料y吨 合计
公路运费(元)
铁路运费(元)
价值(元)
1.5(20X)
1.2(110X)
1.5(10Y)
1.2(120Y)
1.5(20X+10Y)
1.2(110X+120Y)
8000X
1000Y
由上表可列方程组
解这个方程组,得 :
销售款为:
原料费为:
运输费为:
8000X300=2400000(元)
1000X400=400000(元)
15000+97200=112200(元)
所以销售款比原料费与运输费的和多:
2400000-(400000+112200)=1887800(元)
答:销售款比原料费与运输费的和多1887800元。
20x+40y=148
8.3 实际问题与二元一次方程组
练一练
1.买10支笔和15本笔记本需58元,买20支笔和40本笔记本需148元,问每支笔和每本笔记本各多少钱?
解:设每支笔x元,每本笔记y元。
根据题意得
10x+15y=58
解这个方程组,得
y=3.2
x=1
答:每支笔是1元,每本笔记本是3.2元
8.3 实际问题与二元一次方程组
练一练
2.有大小两种货车,2辆大车与3辆小车一次可以运货15.5吨;5辆大车与6辆小车一次可以支货35吨;3辆大车与5辆小车一次可以运货多少吨?
5x+6y=35
解:设每辆大车可运货x吨,每辆小车可运货y吨。
根据题意得
2x+3y=15.5
解这个方程组,得
y=2.5
x=4
所以,3辆大车与5辆小车一次可以运货:
3×4+5×2.5=24.5吨
8.3 实际问题与二元一次方程组
溶液问题
把浓度分别是90%与60%的甲乙两种酒精溶液,配制成浓度为75%的消毒酒精溶液500克,求甲、乙两种酒精溶液各取多少克?
分析:
1.溶液的配制过程中两种溶液的质量和是配置后溶液的质量;
2.配制过程中,纯酒精的量不变。
酒精浓度
纯酒精量
酒精溶液质量
×100%
=
8.3 实际问题与二元一次方程组
练一练
要把浓度为10%的盐水,稀释成浓度为0.9%的生理盐水100kg,需要浓度10%盐水、水各多少千克?
10%x=0.9%×100
解:设需要浓度10%的盐水xkg,水ykg。
根据题意得
x+y=100
解这个方程组,得
y=91
x=9
所以,需要浓度10%的盐水9kg,水91kg
1. 一个长方形,它的长减少4cm,宽增2cm,所得的是一个正方形,它的面积与长方形的面积相等,求原长方形的长与宽。
牛刀小试
2. 小龙在拼图时,发现8个一样大的小长
方形,恰好可以拼成一个大长方形,如图甲所示,
小明看见了说“我来试一试”,结果小明七拼八凑,
拼成一个如图乙的正方形,中间留下一个洞,恰
好是边长2mm的小正方形,你能算出小长方形
的长和宽吗?
甲
乙
牛刀小试
3. 有大小两种货车,2辆大车与3辆小车
一次可以运货15.50吨,5辆大车与6辆小
车一次可以运货35吨。
求:3辆大车与5辆小车一次可以运货
多少吨
分析:要解决这个问题的关键是求每辆
大车和每辆小车一次可运货多少吨
解决此题的
关键是什么?
牛刀小试
4.某车间有90名工人,每人每天平均能生产螺栓15个或螺帽24个,要使一个螺栓配套两个螺帽,应如何分配工人才能使螺栓和螺帽刚好配套?设生产螺栓x人,生产螺帽y人,列方程组为( )
A B、
C、 D、
c
学习致用
一船顺水航行45千米需要3小时,逆水航行65千米需要5小时,若设船在静水中的速度为x千米/小时,水流的速度为y㎞/h,则x、y的值为 ( ) A、X=3,y=2 B、x=14,y=1 C、x=15,y=1 E、x=14,y=2
B
学习致用
