相似形的复习题（无答案）

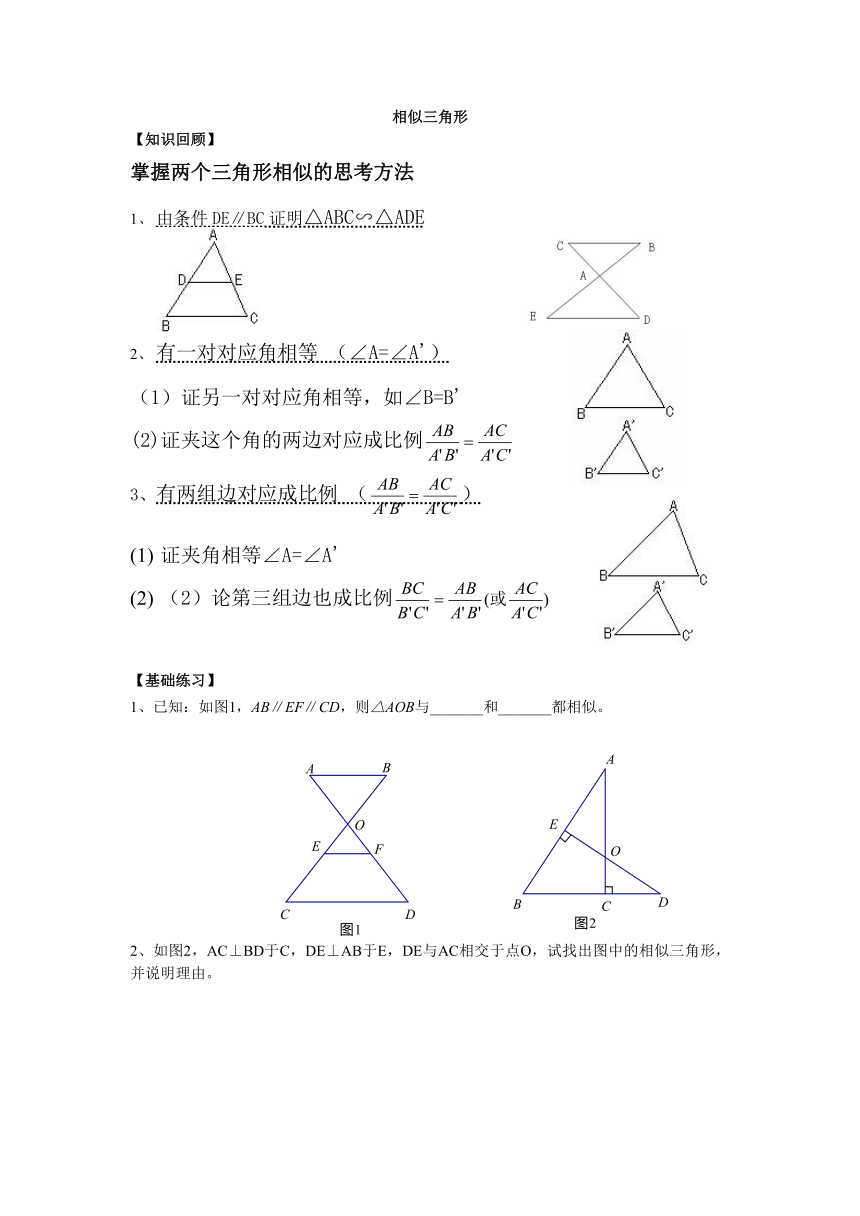
相似三角形
【知识回顾】
掌握两个三角形相似的思考方法
由条件DE∥BC证明△ABC∽△ADE
有一对对应角相等 （∠A=∠A'）
（1）证另一对对应角相等，如∠B=B'
(2)证夹这个角的两边对应成比例
3、有两组边对应成比例 （）
证夹角相等∠A=∠A'
（2）论第三组边也成比例
【基础练习】
1、已知：如图1，AB∥EF∥CD，则△AOB与_______和_______都相似。
2、如图2，AC⊥BD于C，DE⊥AB于E，DE与AC相交于点O，试找出图中的相似三角形，并说明理由。
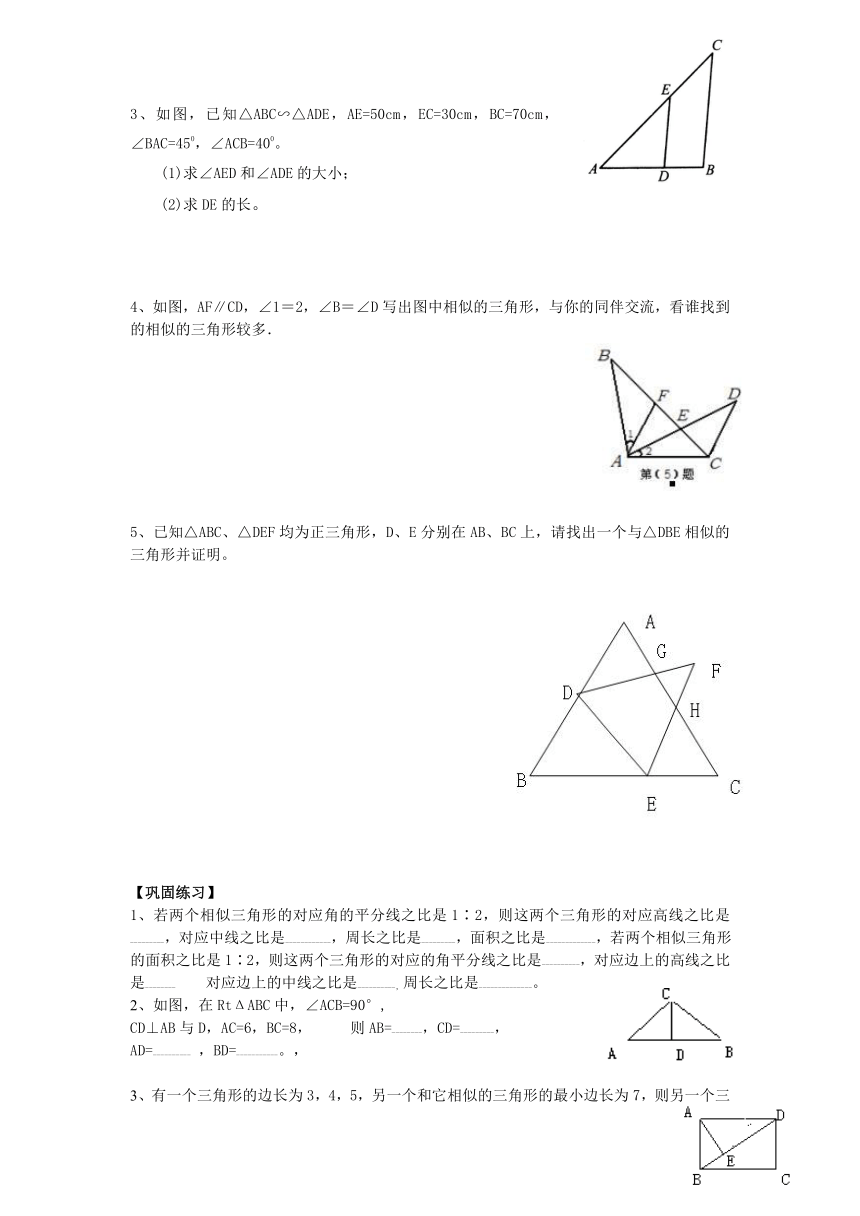
3、如图，已知△ABC∽△ADE，AE=50cm，EC=30cm，BC=70cm，∠BAC=450，∠ACB=400。
(1)求∠AED和∠ADE的大小；
(2)求DE的长。
4、如图，AF∥CD，∠1＝2，∠B＝∠D写出图中相似的三角形，与你的同伴交流，看谁找到的相似的三角形较多．
5、已知△ABC、△DEF均为正三角形，D、E分别在AB、BC上，请找出一个与△DBE相似的三角形并证明。
【巩固练习】
1、若两个相似三角形的对应角的平分线之比是1∶2，则这两个三角形的对应高线之比是---------，对应中线之比是------------，周长之比是---------，面积之比是-------------，若两个相似三角形的面积之比是1∶2，则这两个三角形的对应的角平分线之比是----------，对应边上的高线之比是-------- 对应边上的中线之比是----------，周长之比是--------------。
2、如图，在RtΔABC中，∠ACB=90°,
CD⊥AB与D，AC=6，BC=8， 则AB=--------，CD=---------，
AD=---------- ，BD=-----------。，
3、有一个三角形的边长为3，4，5，另一个和它相似的三角形的最小边长为7，则另一个三角形的周长为----------，面积是-------------
4、如图，矩形ABCD中，AE⊥BD于E，若BE=4，DE=9,则矩形的面积是-----------
5、平行四边形ABCD中，E为BA延长线上的一点，CE交AD于F点，若AE∶AB=1∶3
则SABCF∶SCDF=---------
6、如图，已知，平行四边形ABCD,CE＝BC,S△AFD＝16cm2 , 则S△CEF＝ ,
平行四边形ABCD的面积＿＿＿
7、M在AB上，且MB＝4，AB＝12，AC＝16，
在AC上有一定N，使△AMN与原三角形相似，则AN的长为
8、 如图，△ABC中，DE∥AC，BD＝10，DA＝15， A
BE＝12，则EC＝ ，DE:AC＝ ， D
S△BDE：S梯形ADEC＝
B E C
9、点P为△ABC的AB边上一点（AB>AC），下列条件中不一定能保证△ACP∽△ABC的是（ ）
（A）∠ACP＝∠B（B）∠APC＝∠ACB（C）=（D）=
10、在平行四边形ABCD中，E为AB中点，EF交AC于G，交AD于F，=则的比值是（ 　）（A）2 （B）3 （C）4 （D）5
11、如图，已知是矩形的边上一点，于，试说明：．
12、如图，已知ΔABC中，AD为BC边中线，E为AD上一点，并且CE=CD,
∠EAC=∠B,求证：ΔAEC∽ΔBDA
13、M在AB上，且MB＝4,AB＝12,AC＝16.在AC上求作一点N,
使△AMN与原三角形相似，并求AN的长.
14、已知：如图，△ABC中，D为AB上一点，且，AE⊥CD于E，AF⊥BC于F，求证：
15、如图，四边形ABCD、DEFG都是正方形，连接AE、CG,AE与CG相交于点M，CG与AD相交于点N.
求证：
（第11题）
（第15题）