2011—2012学年第一学期期末学业水平测试九年级上数学试题(含答案)
文档属性
| 名称 | 2011—2012学年第一学期期末学业水平测试九年级上数学试题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 210.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-31 00:00:00 | ||
图片预览

文档简介
2011—2012学年第一学期期末学业水平测试
九年级数学试题
(120分钟 120分)
一 选择题:(每题3分,共36分)
1. 下列命题中的真命题是( ).
A. 对角线互相垂直的四边形是菱形
B. 中心对称图形都是轴对称图形
C. 两条对角线相等的梯形是等腰梯形
D. 等腰梯形是中心对称图形
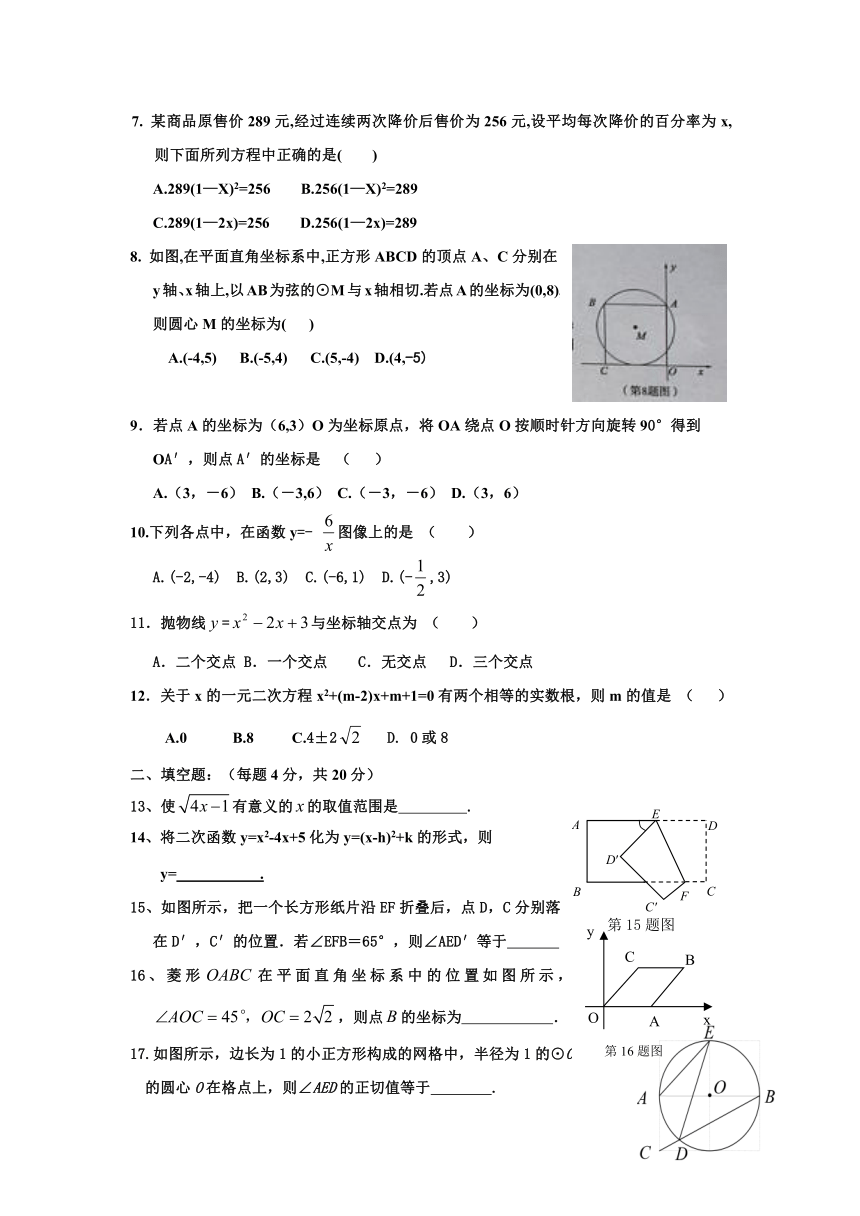
2. 如右图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为( )
A.2cm B.cm C.cm D.cm
3. 如图,BD是⊙O的直径,∠CBD=,则∠A的度数( ).
A.30 B.45 C.60 D.75
4. 已知二次函数y=ax2+bx+c的图像如图所示,则下列条件正确的是( )
A.ac<0 B.b2 -4ac<0
C. b>0 D. a>0,b<0,c>0
5. 抛物线y= x2 向左平移8个单位,再向下平移 9个单位后,所得抛物线的表达式是( )
A. y= (x+8)2-9 B. y= (x-8)2+9
C. y= (x-8)2-9 D. y= (x+8)2+9
6. 如图,在平面直角坐标系中,长、宽分别为2和1的矩形ABCD的边上有一动点P,沿A→B→C→D→A运动一周,则点P的纵坐标y与P所走过的路程x之间的函数关系用图象表示大致是( )
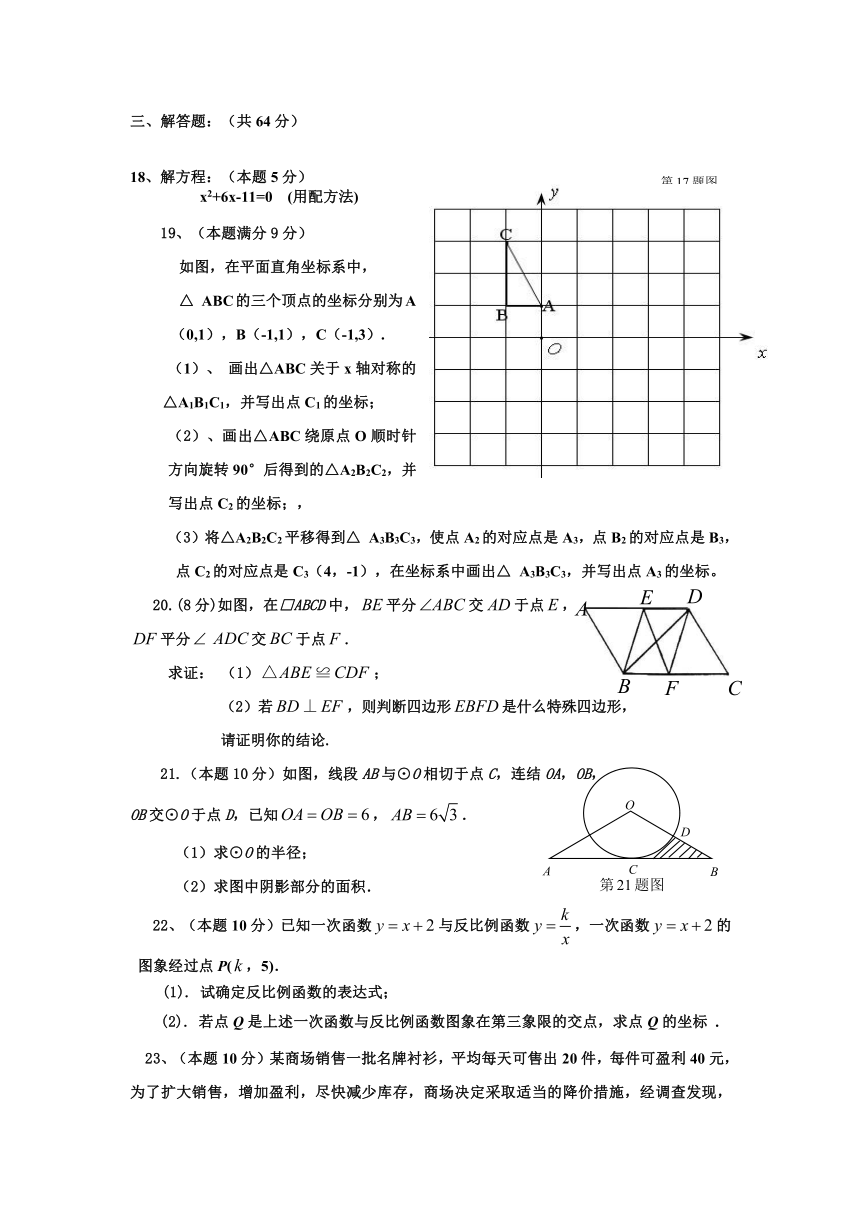
7. 某商品原售价289元,经过连续两次降价后售价为256元,设平均每次降价的百分率为x,则下面所列方程中正确的是( )
A.289(1—X)2=256 B.256(1—X)2=289
C.289(1—2x)=256 D.256(1—2x)=289
8. 如图,在平面直角坐标系中,正方形ABCD的顶点A、C分别在y轴、x轴上,以AB为弦的⊙M与x轴相切.若点A的坐标为(0,8),则圆心M的坐标为( )
A.(-4,5) B.(-5,4) C.(5,-4) D.(4,-5)
9.若点A的坐标为(6,3)O为坐标原点,将OA绕点O按顺时针方向旋转90°得到
OA′,则点A′的坐标是 ( )
A.(3,-6) B.(-3,6) C.(-3,-6) D.(3,6)
10.下列各点中,在函数y=- 图像上的是 ( )
A.(-2,-4) B.(2,3) C.(-6,1) D.(-,3)
11.抛物线=与坐标轴交点为 ( )
A.二个交点 B.一个交点 C.无交点 D.三个交点
12.关于x的一元二次方程x2+(m-2)x+m+1=0有两个相等的实数根,则m的值是 ( )
A.0 B.8 C.4±2 D. 0或8
二、填空题:(每题4分,共20分)
13、使有意义的的取值范围是 .
14、将二次函数y=x2-4x+5化为y=(x-h)2+k的形式,则
y= .
15、如图所示,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠EFB=65°,则∠AED′等于
16、菱形在平面直角坐标系中的位置如图所示,,则点的坐标为 .
17.如图所示,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的正切值等于 .
三、解答题:(共64分)
18、解方程:(本题5分)
x2+6x-11=0 (用配方法)
19、(本题满分9分)
如图,在平面直角坐标系中,
△ ABC的三个顶点的坐标分别为A(0,1),B(-1,1),C(-1,3).
(1)、 画出△ABC关于x轴对称的 △A1B1C1,并写出点C1的坐标;
(2)、画出△ABC绕原点O顺时针方向旋转90°后得到的△A2B2C2,并写出点C2的坐标;,
(3)将△A2B2C2平移得到△ A3B3C3,使点A2的对应点是A3,点B2的对应点是B3,点C2的对应点是C3(4,-1),在坐标系中画出△ A3B3C3,并写出点A3的坐标。
20.(8分)如图,在□ABCD中,平分交于点,
平分交于点.
求证: (1);
(2)若,则判断四边形是什么特殊四边形,
请证明你的结论.
21.(本题10分)如图,线段AB与⊙O相切于点C,连结OA,OB,
OB交⊙O于点D,已知,.
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
22、(本题10分)已知一次函数与反比例函数,一次函数的图象经过点P(,5).
(1). 试确定反比例函数的表达式;
(2). 若点Q是上述一次函数与反比例函数图象在第三象限的交点,求点Q的坐标 .
23、(本题10分)某商场销售一批名牌衬衫,平均每天可售出20件,每件可盈利40元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件每降价1元,平均每天多售2件。
(1) 若商场平均每天要盈利1200元,每件衬衫应降价多少元?
(2) 每件衬衫降价多少元时,商场平均每天盈利最多?
24、(本题12分)
如图,抛物线y=x2+bx-2与x轴交于A,B两点,与y轴交于C点,且A(-1,0).
(1) 求抛物线的解析式及顶点D的坐标;
(2) 判断的形状,证明你的结论;
(3) 点是x轴上的一个动点,当MC+MD的值最小时,求m的值.
九年级数学学科参考答案
选择题:(每题3分,共36分)
1.C 2.C 3.C 4. D 5.A 6.D 7.A 8.A 9.A 10.C 11.B 12.D
二、填空题:(每题4分,共20分)
13.x≥ 14.y=(x-2)2+1 15.50° 16.(2+2,2) 17.
三、解答题:(共64分)
18. (本题5分) x1=-3+2,x2=-3-2
19.(本题满分9分)
说明:三个图形各2分,点的坐标各1分
(1)C1(-1,-3) (2)C2(3,1) (3)A3(2,-2)
20、 证明:(1)∵四边形是平行四边,
∴
∵平分平分
∴……………………… 2分
∴ …………… 4分
(2) 由得 …………5分
在平行四边形中,
∴
∴四边形是平行四边形………7分
若则四边形是菱形…(8分)
21、(1) 连结OC,∵AB与⊙O相切于点C
∴.
∵,
∴.
在中,.
∴ ⊙O的半径为3. … (5分)
(2) 在中∵ OC=, ∴ ∠B=30o, ∠COD=60o.
∴扇形OCD的面积为
==π.… (7分)
∴阴影部分的面积为
=-=-.… (10分)
22、解:(1)因一次函数的图象经过点P(,5),
所以得,解得
所以反比例函数的表达式为……………………………4分
(2)联立……得方程组 解得 或
故第三象限的交点Q的坐标为…………………10分
23、 解:(1)设每件衬衫降价x元,则多售2x件.
根据题意,可得
(40-x)(20+x)=1200
整理得,x2-30x+200=0
解得:x1=10,x2=20.
因要尽快减少库存,故x=20 …………………4分
(2)设商场平均每天盈利y元,则
y=(40-x)(20+2x)=-2x2+60x+800=-2(x2-30x-400)
=-2〔(x-15)2-625〕=-2(x-15)2+1250
∵-2(x-15)2≤0 ∴-2(x-15)2+1250≤1250
∴当x=15时,y取最大值,最大利润为1250元. …………………10分
24、(1)把点A(-1,0)的坐标代入抛物线的解析式y=x2+b-2,整理后解得,
所以抛物线的解析式为 .
顶点. …………………………………3分
(2).,,.
是直角三角形. …………………………………6分
(3) 作出点关于轴的对称点,则,.连接交轴于点,
根据轴对称性及两点之间线段最短可知,的值最小.
设抛物线的对称轴交轴于点..
.. ( http: / / www. / ).………………… 12分
说明:此处求出、D的解析式后,再求与x轴的交点坐标可同样给分.
第2题图
第3题图
第4题图
E
D
B
C′
F
C
D′
A
第15题图
x
y
O
C
B
A
第16题图
第17题图
第21题图
C
O
A
B
D
九年级数学试题
(120分钟 120分)
一 选择题:(每题3分,共36分)
1. 下列命题中的真命题是( ).
A. 对角线互相垂直的四边形是菱形
B. 中心对称图形都是轴对称图形
C. 两条对角线相等的梯形是等腰梯形
D. 等腰梯形是中心对称图形
2. 如右图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为( )
A.2cm B.cm C.cm D.cm
3. 如图,BD是⊙O的直径,∠CBD=,则∠A的度数( ).
A.30 B.45 C.60 D.75
4. 已知二次函数y=ax2+bx+c的图像如图所示,则下列条件正确的是( )
A.ac<0 B.b2 -4ac<0
C. b>0 D. a>0,b<0,c>0
5. 抛物线y= x2 向左平移8个单位,再向下平移 9个单位后,所得抛物线的表达式是( )
A. y= (x+8)2-9 B. y= (x-8)2+9
C. y= (x-8)2-9 D. y= (x+8)2+9
6. 如图,在平面直角坐标系中,长、宽分别为2和1的矩形ABCD的边上有一动点P,沿A→B→C→D→A运动一周,则点P的纵坐标y与P所走过的路程x之间的函数关系用图象表示大致是( )
7. 某商品原售价289元,经过连续两次降价后售价为256元,设平均每次降价的百分率为x,则下面所列方程中正确的是( )
A.289(1—X)2=256 B.256(1—X)2=289
C.289(1—2x)=256 D.256(1—2x)=289
8. 如图,在平面直角坐标系中,正方形ABCD的顶点A、C分别在y轴、x轴上,以AB为弦的⊙M与x轴相切.若点A的坐标为(0,8),则圆心M的坐标为( )
A.(-4,5) B.(-5,4) C.(5,-4) D.(4,-5)
9.若点A的坐标为(6,3)O为坐标原点,将OA绕点O按顺时针方向旋转90°得到
OA′,则点A′的坐标是 ( )
A.(3,-6) B.(-3,6) C.(-3,-6) D.(3,6)
10.下列各点中,在函数y=- 图像上的是 ( )
A.(-2,-4) B.(2,3) C.(-6,1) D.(-,3)
11.抛物线=与坐标轴交点为 ( )
A.二个交点 B.一个交点 C.无交点 D.三个交点
12.关于x的一元二次方程x2+(m-2)x+m+1=0有两个相等的实数根,则m的值是 ( )
A.0 B.8 C.4±2 D. 0或8
二、填空题:(每题4分,共20分)
13、使有意义的的取值范围是 .
14、将二次函数y=x2-4x+5化为y=(x-h)2+k的形式,则
y= .
15、如图所示,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠EFB=65°,则∠AED′等于
16、菱形在平面直角坐标系中的位置如图所示,,则点的坐标为 .
17.如图所示,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的正切值等于 .
三、解答题:(共64分)
18、解方程:(本题5分)
x2+6x-11=0 (用配方法)
19、(本题满分9分)
如图,在平面直角坐标系中,
△ ABC的三个顶点的坐标分别为A(0,1),B(-1,1),C(-1,3).
(1)、 画出△ABC关于x轴对称的 △A1B1C1,并写出点C1的坐标;
(2)、画出△ABC绕原点O顺时针方向旋转90°后得到的△A2B2C2,并写出点C2的坐标;,
(3)将△A2B2C2平移得到△ A3B3C3,使点A2的对应点是A3,点B2的对应点是B3,点C2的对应点是C3(4,-1),在坐标系中画出△ A3B3C3,并写出点A3的坐标。
20.(8分)如图,在□ABCD中,平分交于点,
平分交于点.
求证: (1);
(2)若,则判断四边形是什么特殊四边形,
请证明你的结论.
21.(本题10分)如图,线段AB与⊙O相切于点C,连结OA,OB,
OB交⊙O于点D,已知,.
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
22、(本题10分)已知一次函数与反比例函数,一次函数的图象经过点P(,5).
(1). 试确定反比例函数的表达式;
(2). 若点Q是上述一次函数与反比例函数图象在第三象限的交点,求点Q的坐标 .
23、(本题10分)某商场销售一批名牌衬衫,平均每天可售出20件,每件可盈利40元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件每降价1元,平均每天多售2件。
(1) 若商场平均每天要盈利1200元,每件衬衫应降价多少元?
(2) 每件衬衫降价多少元时,商场平均每天盈利最多?
24、(本题12分)
如图,抛物线y=x2+bx-2与x轴交于A,B两点,与y轴交于C点,且A(-1,0).
(1) 求抛物线的解析式及顶点D的坐标;
(2) 判断的形状,证明你的结论;
(3) 点是x轴上的一个动点,当MC+MD的值最小时,求m的值.
九年级数学学科参考答案
选择题:(每题3分,共36分)
1.C 2.C 3.C 4. D 5.A 6.D 7.A 8.A 9.A 10.C 11.B 12.D
二、填空题:(每题4分,共20分)
13.x≥ 14.y=(x-2)2+1 15.50° 16.(2+2,2) 17.
三、解答题:(共64分)
18. (本题5分) x1=-3+2,x2=-3-2
19.(本题满分9分)
说明:三个图形各2分,点的坐标各1分
(1)C1(-1,-3) (2)C2(3,1) (3)A3(2,-2)
20、 证明:(1)∵四边形是平行四边,
∴
∵平分平分
∴……………………… 2分
∴ …………… 4分
(2) 由得 …………5分
在平行四边形中,
∴
∴四边形是平行四边形………7分
若则四边形是菱形…(8分)
21、(1) 连结OC,∵AB与⊙O相切于点C
∴.
∵,
∴.
在中,.
∴ ⊙O的半径为3. … (5分)
(2) 在中∵ OC=, ∴ ∠B=30o, ∠COD=60o.
∴扇形OCD的面积为
==π.… (7分)
∴阴影部分的面积为
=-=-.… (10分)
22、解:(1)因一次函数的图象经过点P(,5),
所以得,解得
所以反比例函数的表达式为……………………………4分
(2)联立……得方程组 解得 或
故第三象限的交点Q的坐标为…………………10分
23、 解:(1)设每件衬衫降价x元,则多售2x件.
根据题意,可得
(40-x)(20+x)=1200
整理得,x2-30x+200=0
解得:x1=10,x2=20.
因要尽快减少库存,故x=20 …………………4分
(2)设商场平均每天盈利y元,则
y=(40-x)(20+2x)=-2x2+60x+800=-2(x2-30x-400)
=-2〔(x-15)2-625〕=-2(x-15)2+1250
∵-2(x-15)2≤0 ∴-2(x-15)2+1250≤1250
∴当x=15时,y取最大值,最大利润为1250元. …………………10分
24、(1)把点A(-1,0)的坐标代入抛物线的解析式y=x2+b-2,整理后解得,
所以抛物线的解析式为 .
顶点. …………………………………3分
(2).,,.
是直角三角形. …………………………………6分
(3) 作出点关于轴的对称点,则,.连接交轴于点,
根据轴对称性及两点之间线段最短可知,的值最小.
设抛物线的对称轴交轴于点..
.. ( http: / / www. / ).………………… 12分
说明:此处求出、D的解析式后,再求与x轴的交点坐标可同样给分.
第2题图
第3题图
第4题图
E
D
B
C′
F
C
D′
A
第15题图
x
y
O
C
B
A
第16题图
第17题图
第21题图
C
O
A
B
D
同课章节目录
