22.2平行四边形 练习-2020-2021学年沪教版(上海)八年级数学下册(机构)(word版含答案)
文档属性
| 名称 | 22.2平行四边形 练习-2020-2021学年沪教版(上海)八年级数学下册(机构)(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 132.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-31 00:00:00 | ||
图片预览


文档简介
1285875-30289522.2平行四边形
22.2平行四边形
一、选择题
1.如图,已知ABCD是长方形纸片, CD=3 ,在CD上存在一点E,沿直线AE将 △AED 折叠,D恰好落在BC边上的点F处,且 S△AFB=6 ,则 △AED 的面积是(?? ).
A.?253????????????????????????????????????????B.?256????????????????????????????????????????C.?43????????????????????????????????????????D.?23
2.如图,在 ΔABC 中, ∠A=40° , AB=AC ,点 D 在 AC 边上,以 CB , CD 为边作?BCDE,则 ∠E 的度数为 ( ?? )
A.?40°????????????????????????????????????B.?50°????????????????????????????????????C.?60°????????????????????????????????????D.?70°
3.如图,平面直角坐标系中,长方形OABC,点A,C分别在x轴,y轴的正半轴上,点B(6,3),现将△OAB沿OB翻折至△OA′B位置,OA′交BC于点P.则点P的坐标为(?? )
A.?( 94 ,3)??????????????????????B.?( 32 ,3)??????????????????????C.?( 125 ,3)??????????????????????D.?( 52,3 )
4.下列命题是真命题的是(?? )
A.?对角线相等的四边形是平行四边形??????????????????????B.?对角线互相平分且相等的四边形是平行四边形
C.?对角线互相平分的四边形是平行四边形???????????????D.?对角线互相垂直的四边形是平行四边形
5.下列说法不正确的是(? )
A.?两组对边分别相等的四边形是平行四边形???????????B.?对角线相等的平行四边形是矩形
C.?一个角是直角的四边形是矩形????????????????????????????? D.?对角线互相平分且垂直的四边形是菱形
6.如图,菱形ABCD的边长是4cm,且∠ABC=60°,E是BC中点,P点在BD上,则PE+PC的最小值为(?? )cm.
A.?2?????????????????????????????????????????B.?2 3?????????????????????????????????????????C.?3?????????????????????????????????????????D.?4
7.如图,矩形ABCD中,对角线AC、BD相交于点O,过点O作OE⊥BD交AD于点E,已知AB=2, S△DOE=54 ,则AE的长为(?? )
A.?1.5?????????????????????????????????????????B.?2?????????????????????????????????????????C.?2.5?????????????????????????????????????????D.?2
8.如图所示,在矩形纸片ABCD中,AB=3,BC=5.折叠纸片使点A落在边BC上的A′处,折痕为PQ.当点A′在边BC上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在边AB、AD上移动,则点A′在边BC上可移动的最大距离为(?? )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
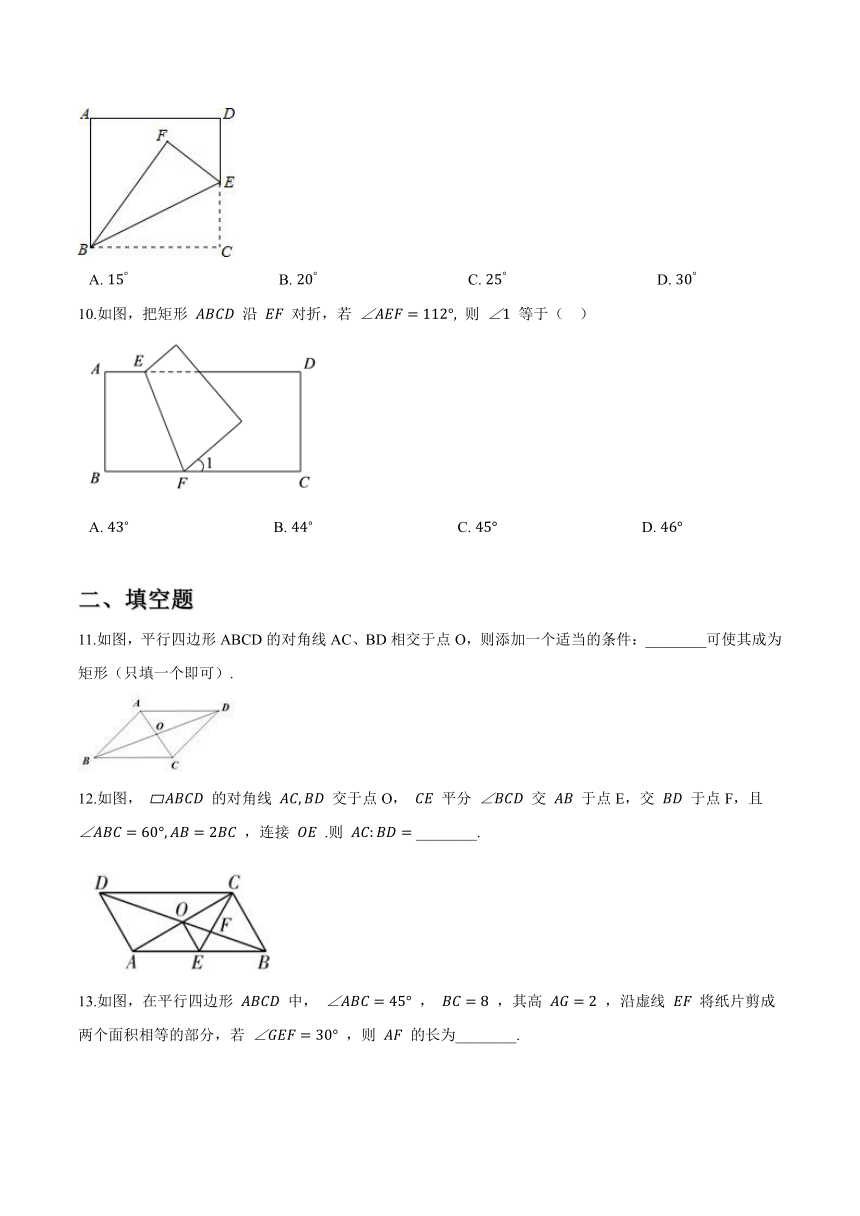
9.如图,在正方形 ABCD 中,E为 DC 边上的一点,沿线段 BE 对折后,若 ∠ABF 比 ∠EBF 大 15° ,则 ∠EBF 的度数为( )
A.?15°???????????????????????????????????????B.?20°???????????????????????????????????????C.?25°???????????????????????????????????????D.?30°
10.如图,把矩形 ABCD 沿 EF 对折,若 ∠AEF=112°, 则 ∠1 等于(?? )
A.?43???????????????????????????????????????B.?44???????????????????????????????????????C.?45°??????????????????????????????????????D.?46°
二、填空题
11.如图,平行四边形ABCD的对角线AC、BD相交于点O,则添加一个适当的条件:________可使其成为矩形(只填一个即可).
12.如图, ?ABCD 的对角线 AC,BD 交于点O, CE 平分 ∠BCD 交 AB 于点E,交 BD 于点F,且 ∠ABC=60°,AB=2BC ,连接 OE .则 AC:BD= ________.
13.如图,在平行四边形 ABCD 中, ∠ABC=45° , BC=8 ,其高 AG=2 ,沿虚线 EF 将纸片剪成两个面积相等的部分,若 ∠GEF=30° ,则 AF 的长为________.
14.如图,AB=AC,四边形AEDF是平行四边形,△CFD和△DEB的周长分别为5和10,则△ABC的周长是________.
三、计算与解答
15.如图,在四边形ABCD中, AD//BC ,E是边BC上一点,AD=BE,DE=DC.求证:∠B=∠C.
16.如图,已知四边形ABCD是矩形,点E在对角线AC上,点F在边CD上(点F与点C、D不重合), BE⊥EF ,且 ∠ABE+∠CEF=45° .求证:四边形ABCD是正方形.
17.如图,在矩形 ABCD 中, BC=8 , ∠ABD=30° ,若点M、N分别是线段 DB 、 AB 上的两个动点,则求 AM+MN 的最小值.
18.如图,在等腰△ABC中,AB=AC,AH⊥BC,点E是AH上一点,延长AH至点F,使FH=EH,
求证:四边形EBFC是菱形.
参考答案
1.【答案】 B 2.【答案】 D 3.【答案】 A 4.【答案】 C 5.【答案】 C 6.【答案】 B 7.【答案】 A 8.【答案】 B 9.【答案】 C 10.【答案】 B
11.【答案】 AC=BD(答案不唯一) 12.【答案】 21:7 13.【答案】 3?3 14.【答案】 15
15.【答案】 证明:∵ AD//BC ,E是边BC上一点,AD=BE,
∴四边形ABED是平行四边形(一组对边平行且相等的四边形是平行四边形),
∴AB//DE
∴ ∠B=∠DEC ,
∵DE=DC,
∴ ∠DEC=∠C ,
∴∠B=∠C.
16.【答案】 证明:如图,作 EM⊥BC 于点M,
∵四边形 ABCD 是矩形,∴ AB⊥BC ,∴ EM//AB ,
∴ ∠ABE=∠BEM , ∠BAC=∠CEM ,∠ABC=90°
∵ ∠ABE+∠CEF=45° ,∴ ∠BEM+∠CEF=45° ,
∵ BE⊥EF ,∴ ∠CEM=45°=∠BAC ,
∴ ∠BAC=∠ACB=45° ,∴ AB=BC
∴矩形 ABCD 是正方形.
17.【答案】 解:作点A关于 BD 的对称点 A′ ,连接 MA′ , BA′ ,过 A′ 作 A′H⊥AB 于H.
∵ BA=BA′ , ∠ABD=∠DBA′=30° ,
∴ ∠ABA′=60° ,
∴ △ABA′ 是等边三角形,
∵四边形 ABCD 是矩形,
∴ AD=BC=8 ,
在 Rt△ABD 中,∠ABD=30°,BC=8,
∴BD=16,AB=?83 ,
∵ A′H⊥AB ,
∴ AH=HB=43 ,
∴ A′H=3AH=12 ,
∵ AM+MN=A′M+MN≥A′H ,
∴ AM+MN≥12 ,
∴ AM+MN 的最小值为12.
18.【答案】 证明:∵△ABC为等腰三角形,AH⊥BC,∴H为BC的中点,
又∵FH=EH,∴四边形BECF为平行四边形.
∵AH⊥BC,∴平行四边形BECF为菱形.
22.2平行四边形
一、选择题
1.如图,已知ABCD是长方形纸片, CD=3 ,在CD上存在一点E,沿直线AE将 △AED 折叠,D恰好落在BC边上的点F处,且 S△AFB=6 ,则 △AED 的面积是(?? ).
A.?253????????????????????????????????????????B.?256????????????????????????????????????????C.?43????????????????????????????????????????D.?23
2.如图,在 ΔABC 中, ∠A=40° , AB=AC ,点 D 在 AC 边上,以 CB , CD 为边作?BCDE,则 ∠E 的度数为 ( ?? )
A.?40°????????????????????????????????????B.?50°????????????????????????????????????C.?60°????????????????????????????????????D.?70°
3.如图,平面直角坐标系中,长方形OABC,点A,C分别在x轴,y轴的正半轴上,点B(6,3),现将△OAB沿OB翻折至△OA′B位置,OA′交BC于点P.则点P的坐标为(?? )
A.?( 94 ,3)??????????????????????B.?( 32 ,3)??????????????????????C.?( 125 ,3)??????????????????????D.?( 52,3 )
4.下列命题是真命题的是(?? )
A.?对角线相等的四边形是平行四边形??????????????????????B.?对角线互相平分且相等的四边形是平行四边形
C.?对角线互相平分的四边形是平行四边形???????????????D.?对角线互相垂直的四边形是平行四边形
5.下列说法不正确的是(? )
A.?两组对边分别相等的四边形是平行四边形???????????B.?对角线相等的平行四边形是矩形
C.?一个角是直角的四边形是矩形????????????????????????????? D.?对角线互相平分且垂直的四边形是菱形
6.如图,菱形ABCD的边长是4cm,且∠ABC=60°,E是BC中点,P点在BD上,则PE+PC的最小值为(?? )cm.
A.?2?????????????????????????????????????????B.?2 3?????????????????????????????????????????C.?3?????????????????????????????????????????D.?4
7.如图,矩形ABCD中,对角线AC、BD相交于点O,过点O作OE⊥BD交AD于点E,已知AB=2, S△DOE=54 ,则AE的长为(?? )
A.?1.5?????????????????????????????????????????B.?2?????????????????????????????????????????C.?2.5?????????????????????????????????????????D.?2
8.如图所示,在矩形纸片ABCD中,AB=3,BC=5.折叠纸片使点A落在边BC上的A′处,折痕为PQ.当点A′在边BC上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在边AB、AD上移动,则点A′在边BC上可移动的最大距离为(?? )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
9.如图,在正方形 ABCD 中,E为 DC 边上的一点,沿线段 BE 对折后,若 ∠ABF 比 ∠EBF 大 15° ,则 ∠EBF 的度数为( )
A.?15°???????????????????????????????????????B.?20°???????????????????????????????????????C.?25°???????????????????????????????????????D.?30°
10.如图,把矩形 ABCD 沿 EF 对折,若 ∠AEF=112°, 则 ∠1 等于(?? )
A.?43???????????????????????????????????????B.?44???????????????????????????????????????C.?45°??????????????????????????????????????D.?46°
二、填空题
11.如图,平行四边形ABCD的对角线AC、BD相交于点O,则添加一个适当的条件:________可使其成为矩形(只填一个即可).
12.如图, ?ABCD 的对角线 AC,BD 交于点O, CE 平分 ∠BCD 交 AB 于点E,交 BD 于点F,且 ∠ABC=60°,AB=2BC ,连接 OE .则 AC:BD= ________.
13.如图,在平行四边形 ABCD 中, ∠ABC=45° , BC=8 ,其高 AG=2 ,沿虚线 EF 将纸片剪成两个面积相等的部分,若 ∠GEF=30° ,则 AF 的长为________.
14.如图,AB=AC,四边形AEDF是平行四边形,△CFD和△DEB的周长分别为5和10,则△ABC的周长是________.
三、计算与解答
15.如图,在四边形ABCD中, AD//BC ,E是边BC上一点,AD=BE,DE=DC.求证:∠B=∠C.
16.如图,已知四边形ABCD是矩形,点E在对角线AC上,点F在边CD上(点F与点C、D不重合), BE⊥EF ,且 ∠ABE+∠CEF=45° .求证:四边形ABCD是正方形.
17.如图,在矩形 ABCD 中, BC=8 , ∠ABD=30° ,若点M、N分别是线段 DB 、 AB 上的两个动点,则求 AM+MN 的最小值.
18.如图,在等腰△ABC中,AB=AC,AH⊥BC,点E是AH上一点,延长AH至点F,使FH=EH,
求证:四边形EBFC是菱形.
参考答案
1.【答案】 B 2.【答案】 D 3.【答案】 A 4.【答案】 C 5.【答案】 C 6.【答案】 B 7.【答案】 A 8.【答案】 B 9.【答案】 C 10.【答案】 B
11.【答案】 AC=BD(答案不唯一) 12.【答案】 21:7 13.【答案】 3?3 14.【答案】 15
15.【答案】 证明:∵ AD//BC ,E是边BC上一点,AD=BE,
∴四边形ABED是平行四边形(一组对边平行且相等的四边形是平行四边形),
∴AB//DE
∴ ∠B=∠DEC ,
∵DE=DC,
∴ ∠DEC=∠C ,
∴∠B=∠C.
16.【答案】 证明:如图,作 EM⊥BC 于点M,
∵四边形 ABCD 是矩形,∴ AB⊥BC ,∴ EM//AB ,
∴ ∠ABE=∠BEM , ∠BAC=∠CEM ,∠ABC=90°
∵ ∠ABE+∠CEF=45° ,∴ ∠BEM+∠CEF=45° ,
∵ BE⊥EF ,∴ ∠CEM=45°=∠BAC ,
∴ ∠BAC=∠ACB=45° ,∴ AB=BC
∴矩形 ABCD 是正方形.
17.【答案】 解:作点A关于 BD 的对称点 A′ ,连接 MA′ , BA′ ,过 A′ 作 A′H⊥AB 于H.
∵ BA=BA′ , ∠ABD=∠DBA′=30° ,
∴ ∠ABA′=60° ,
∴ △ABA′ 是等边三角形,
∵四边形 ABCD 是矩形,
∴ AD=BC=8 ,
在 Rt△ABD 中,∠ABD=30°,BC=8,
∴BD=16,AB=?83 ,
∵ A′H⊥AB ,
∴ AH=HB=43 ,
∴ A′H=3AH=12 ,
∵ AM+MN=A′M+MN≥A′H ,
∴ AM+MN≥12 ,
∴ AM+MN 的最小值为12.
18.【答案】 证明:∵△ABC为等腰三角形,AH⊥BC,∴H为BC的中点,
又∵FH=EH,∴四边形BECF为平行四边形.
∵AH⊥BC,∴平行四边形BECF为菱形.
