第20章 一次函数(三) 单元复习测试-2020-2021学年沪教版(上海)八年级数学下册(机构)(Word版 含答案)
文档属性
| 名称 | 第20章 一次函数(三) 单元复习测试-2020-2021学年沪教版(上海)八年级数学下册(机构)(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 105.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-01 10:07:12 | ||
图片预览

文档简介
1162685-302895第二十章 一次函数复习与测试3
第二十章 一次函数复习与测试3
一、选择题
1.点 A(a,y1) 、 B(2a,y2) 都在一次函数 y=?2ax+a(a≠0) 的图象上,则 y1 、 y2 的大小关系是(?? )
A.?y1>y2???????????????????????????????B.?y1=y2???????????????????????????????C.?y12.一次函数 y=?3x+2 的图象经过(?? )
A.?第一、二、三象限?????????B.?第一、三、四象限?????????C.?第二、三、四象限?????????D.?第一、二、四象限
3.如图所示是函数 y=kx+b 与 y=mx+n 的图象,则方程组 {y=kx+by=mx+n 的解是(?? )
A.?x=4 , y=3???????????B.?x=?4 , y=?3???????????C.?x=3 , y=4???????????D.?x=?3 , y=?4
4.如图,在平面直角坐标系中,点A(- 2,2),B(2,6),点P为x轴上一点,当PA+PB的值最小时,三角形PAB的面积为(??? )
A.?1???????????????????????????????????????????B.?6???????????????????????????????????????????C.?8???????????????????????????????????????????D.?12
5.一次函数y= 2x+1的图象经过点( ???)
A.?(-1,-2)??????????????????????????????B.?(-1,-1)??????????????????????????????C.?(0,-1)??????????????????????????????D.?(1,1)
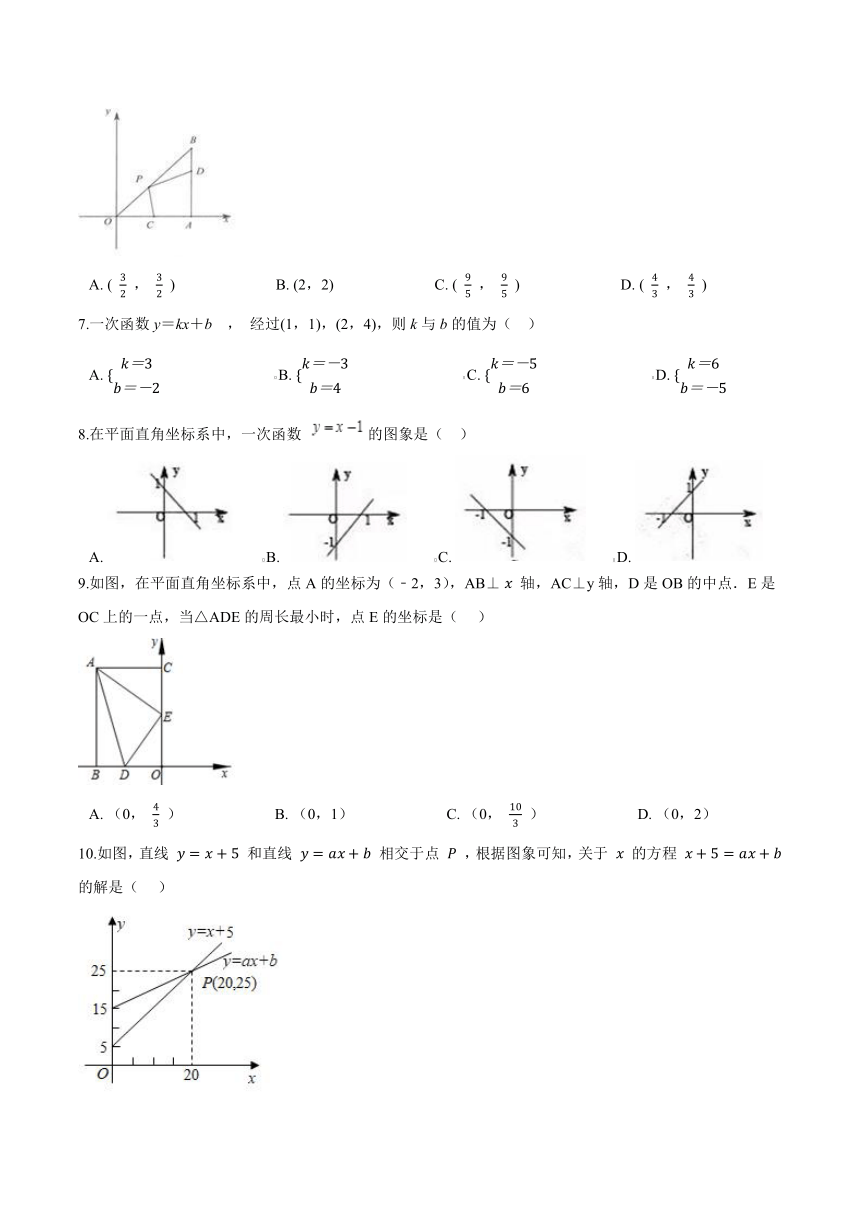
6.如图,在Rt△ABO中,∠OAB=90°,B(3,3),点D在边AB上,AD=2BD,点C为OA的中点,点P为边OB上的动点,若四边形PCAD周长最小,则点P的坐标为(??? )
A.?( 32 , 32 )??????????????????????????B.?(2,2)??????????????????????????C.?( 95 , 95 )??????????????????????????D.?( 43 , 43 )
7.一次函数y=kx+b , 经过(1,1),(2,4),则k与b的值为(?? )
A.?{k=3b=-2??????????????????????????????B.?{k=-3b=4??????????????????????????????C.?{k=-5b=6??????????????????????????????D.?{k=6b=-5
8.在平面直角坐标系中,一次函数 的图象是(?? )
A.????????B.????????C.????????D.?
9.如图,在平面直角坐标系中,点A的坐标为(﹣2,3),AB⊥ x 轴,AC⊥y轴,D是OB的中点.E是OC上的一点,当△ADE的周长最小时,点E的坐标是(??? )
A.?(0, 43 )????????????????????????B.?(0,1)????????????????????????C.?(0, 103 )????????????????????????D.?(0,2)
10.如图,直线 y=x+5 和直线 y=ax+b 相交于点 P ,根据图象可知,关于 x 的方程 x+5=ax+b 的解是(??? )
A.?x=20???????????????????????????????B.?x=25???????????????????????????????C.?x=?25???????????????????????????????D.?x=?20
二、填空题
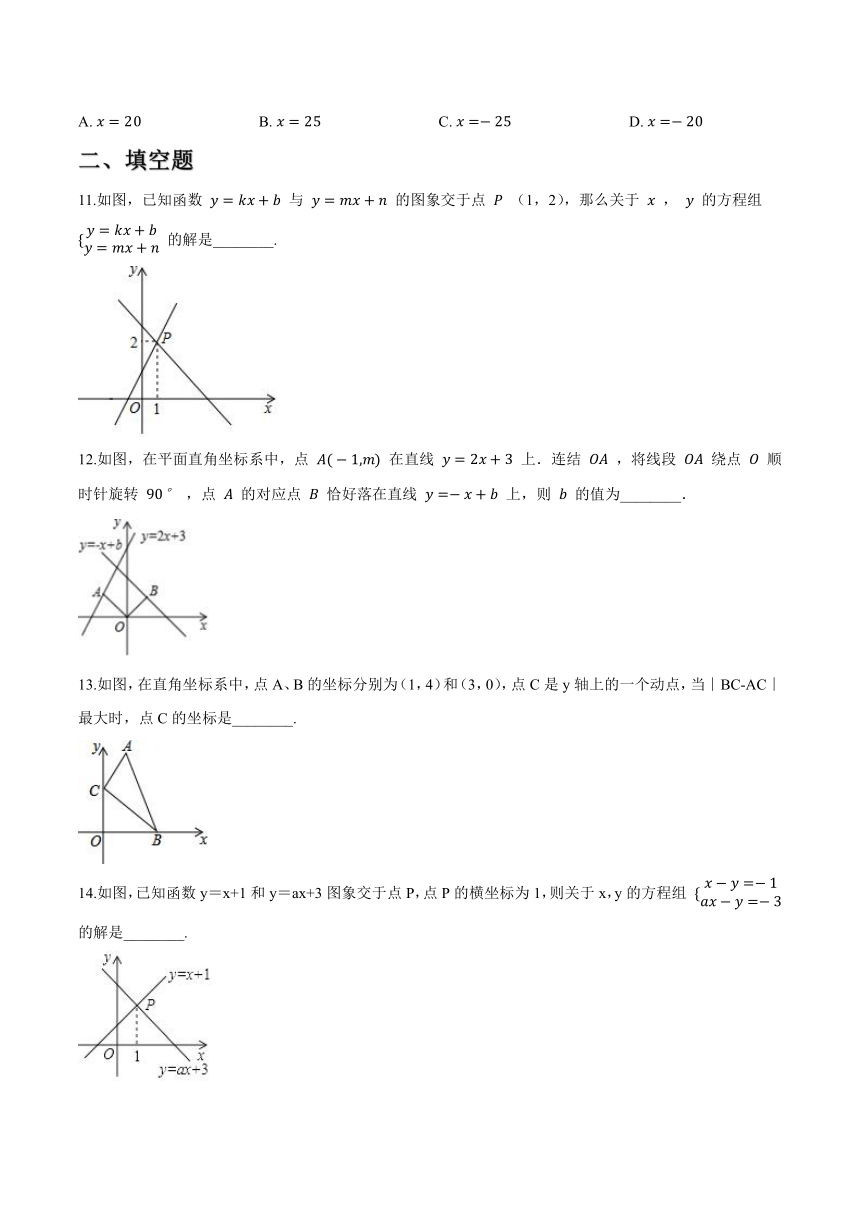
11.如图,已知函数 y=kx+b 与 y=mx+n 的图象交于点 P (1,2),那么关于 x , y 的方程组 {y=kx+by=mx+n 的解是________.
12.如图,在平面直角坐标系中,点 A(?1,m) 在直线 y=2x+3 上.连结 OA ,将线段 OA 绕点 O 顺时针旋转 90° ,点 A 的对应点 B 恰好落在直线 y=?x+b 上,则 b 的值为________.
13.如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,当∣BC-AC∣最大时,点C的坐标是________.
14.如图,已知函数y=x+1和y=ax+3图象交于点P,点P的横坐标为1,则关于x,y的方程组 {x?y=?1ax?y=?3 的解是________.
三、计算与解答
15.若 y?1 与x+1成正比例,且x=1时y=5,求y与x的函数表达式.
16.如图,D为反比例函数 y=kx(k<0) 的图象上一点,过D作DE⊥x轴于点E , DC⊥y轴于点C , 一次函数y=-x+2的图象经过C点,与x轴相交于A点,四边形DCAE的面积为4,求k的值.
17.如图,直线y=﹣ 43 x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的解析式为________.(要求:写出解题过程)
18.在给出的网格中画出一次函数 y=2x?3 的图象,并结合图象求:
①方程 2x?3=0 的解;
②不等式 2x?3>0 的解集;
③不等式 ?1<2x?3<5 的解集.
参考答案
1.【答案】 A 2.【答案】 D 3.【答案】 C 4.【答案】 B 5.【答案】 B 6.【答案】 C 7.【答案】 A 8.【答案】 B 9.【答案】 B 10.【答案】 A
11.【答案】 {x=1y=2
12.【答案】 2
13.【答案】 (0,6)
14.【答案】 {x=1y=2
15.【答案】 解:由 y?1 与x+1成正比例,
所以设: y?1=k(x+1)(k≠0),
把 x=1,y=5 代入得: 2k=4,
∴k=2, ?
所以:y与x的函数表达式: y?1=2(x+1),
即 y=2x+3.
16.【答案】 解:由于一次函数y=-x+2的图象经过C点,与x轴相交于A点,
则可求得A(2,0)、C(0,2),即OA=OC=2.
∴S△AOC= 12 ×2×2=2,|k|=S矩形DCOE=4-2=2.
又函数图象位于第二象限,k<0,
则k=-2.
17.【答案】 y=﹣ 12 x+3;解:当x=0时,y=8;当y=0时,x=6, ∴OA=6,OB=8, ∴AB=10, 根据已知得到BM=B'M,AB'=AB=10, ∴OB'=4,设BM=x,则B'M=x,OM=8﹣x, 在直角△B'MO中,x2=(8﹣x)2+42 , ∴x=5, ∴OM=3, 则M(0,3), 设直线AM的解析式为y=kx+b,把M(0,3),A(6,0)代入其中得: {3=b0=6k+b 解得:k=﹣ 12 ,b=3, ∴AM的解析为:y=﹣ 12 x+3.
18.【答案】 解:解:根据题意一次函数 y=2x?3 的图象如下:
①根据函数图象可知一次函数 y=2x?3 与x轴的交点为( 32 ,0)
∴方程 2x?3=0 的解为x= 32 ;
②根据函数图象可知不等式 2x?3>0 的解集为:x> 32 ;
③根据函数图象可知当x=1,时y=-1,当x=4,时y=5
∴不等式 ?1<2x?3<5 的解集为:1
第二十章 一次函数复习与测试3
一、选择题
1.点 A(a,y1) 、 B(2a,y2) 都在一次函数 y=?2ax+a(a≠0) 的图象上,则 y1 、 y2 的大小关系是(?? )
A.?y1>y2???????????????????????????????B.?y1=y2???????????????????????????????C.?y1
A.?第一、二、三象限?????????B.?第一、三、四象限?????????C.?第二、三、四象限?????????D.?第一、二、四象限
3.如图所示是函数 y=kx+b 与 y=mx+n 的图象,则方程组 {y=kx+by=mx+n 的解是(?? )
A.?x=4 , y=3???????????B.?x=?4 , y=?3???????????C.?x=3 , y=4???????????D.?x=?3 , y=?4
4.如图,在平面直角坐标系中,点A(- 2,2),B(2,6),点P为x轴上一点,当PA+PB的值最小时,三角形PAB的面积为(??? )
A.?1???????????????????????????????????????????B.?6???????????????????????????????????????????C.?8???????????????????????????????????????????D.?12
5.一次函数y= 2x+1的图象经过点( ???)
A.?(-1,-2)??????????????????????????????B.?(-1,-1)??????????????????????????????C.?(0,-1)??????????????????????????????D.?(1,1)
6.如图,在Rt△ABO中,∠OAB=90°,B(3,3),点D在边AB上,AD=2BD,点C为OA的中点,点P为边OB上的动点,若四边形PCAD周长最小,则点P的坐标为(??? )
A.?( 32 , 32 )??????????????????????????B.?(2,2)??????????????????????????C.?( 95 , 95 )??????????????????????????D.?( 43 , 43 )
7.一次函数y=kx+b , 经过(1,1),(2,4),则k与b的值为(?? )
A.?{k=3b=-2??????????????????????????????B.?{k=-3b=4??????????????????????????????C.?{k=-5b=6??????????????????????????????D.?{k=6b=-5
8.在平面直角坐标系中,一次函数 的图象是(?? )
A.????????B.????????C.????????D.?
9.如图,在平面直角坐标系中,点A的坐标为(﹣2,3),AB⊥ x 轴,AC⊥y轴,D是OB的中点.E是OC上的一点,当△ADE的周长最小时,点E的坐标是(??? )
A.?(0, 43 )????????????????????????B.?(0,1)????????????????????????C.?(0, 103 )????????????????????????D.?(0,2)
10.如图,直线 y=x+5 和直线 y=ax+b 相交于点 P ,根据图象可知,关于 x 的方程 x+5=ax+b 的解是(??? )
A.?x=20???????????????????????????????B.?x=25???????????????????????????????C.?x=?25???????????????????????????????D.?x=?20
二、填空题
11.如图,已知函数 y=kx+b 与 y=mx+n 的图象交于点 P (1,2),那么关于 x , y 的方程组 {y=kx+by=mx+n 的解是________.
12.如图,在平面直角坐标系中,点 A(?1,m) 在直线 y=2x+3 上.连结 OA ,将线段 OA 绕点 O 顺时针旋转 90° ,点 A 的对应点 B 恰好落在直线 y=?x+b 上,则 b 的值为________.
13.如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,当∣BC-AC∣最大时,点C的坐标是________.
14.如图,已知函数y=x+1和y=ax+3图象交于点P,点P的横坐标为1,则关于x,y的方程组 {x?y=?1ax?y=?3 的解是________.
三、计算与解答
15.若 y?1 与x+1成正比例,且x=1时y=5,求y与x的函数表达式.
16.如图,D为反比例函数 y=kx(k<0) 的图象上一点,过D作DE⊥x轴于点E , DC⊥y轴于点C , 一次函数y=-x+2的图象经过C点,与x轴相交于A点,四边形DCAE的面积为4,求k的值.
17.如图,直线y=﹣ 43 x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的解析式为________.(要求:写出解题过程)
18.在给出的网格中画出一次函数 y=2x?3 的图象,并结合图象求:
①方程 2x?3=0 的解;
②不等式 2x?3>0 的解集;
③不等式 ?1<2x?3<5 的解集.
参考答案
1.【答案】 A 2.【答案】 D 3.【答案】 C 4.【答案】 B 5.【答案】 B 6.【答案】 C 7.【答案】 A 8.【答案】 B 9.【答案】 B 10.【答案】 A
11.【答案】 {x=1y=2
12.【答案】 2
13.【答案】 (0,6)
14.【答案】 {x=1y=2
15.【答案】 解:由 y?1 与x+1成正比例,
所以设: y?1=k(x+1)(k≠0),
把 x=1,y=5 代入得: 2k=4,
∴k=2, ?
所以:y与x的函数表达式: y?1=2(x+1),
即 y=2x+3.
16.【答案】 解:由于一次函数y=-x+2的图象经过C点,与x轴相交于A点,
则可求得A(2,0)、C(0,2),即OA=OC=2.
∴S△AOC= 12 ×2×2=2,|k|=S矩形DCOE=4-2=2.
又函数图象位于第二象限,k<0,
则k=-2.
17.【答案】 y=﹣ 12 x+3;解:当x=0时,y=8;当y=0时,x=6, ∴OA=6,OB=8, ∴AB=10, 根据已知得到BM=B'M,AB'=AB=10, ∴OB'=4,设BM=x,则B'M=x,OM=8﹣x, 在直角△B'MO中,x2=(8﹣x)2+42 , ∴x=5, ∴OM=3, 则M(0,3), 设直线AM的解析式为y=kx+b,把M(0,3),A(6,0)代入其中得: {3=b0=6k+b 解得:k=﹣ 12 ,b=3, ∴AM的解析为:y=﹣ 12 x+3.
18.【答案】 解:解:根据题意一次函数 y=2x?3 的图象如下:
①根据函数图象可知一次函数 y=2x?3 与x轴的交点为( 32 ,0)
∴方程 2x?3=0 的解为x= 32 ;
②根据函数图象可知不等式 2x?3>0 的解集为:x> 32 ;
③根据函数图象可知当x=1,时y=-1,当x=4,时y=5
∴不等式 ?1<2x?3<5 的解集为:1
