冀教版九年级上册数学课件 第27章 提分专项(八) 反比例函数中k的几何意义的应用(共27张ppt)
文档属性
| 名称 | 冀教版九年级上册数学课件 第27章 提分专项(八) 反比例函数中k的几何意义的应用(共27张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-30 22:23:27 | ||
图片预览







文档简介
提分专项(八)
反比例函数中k的几何意义的应用
冀教版 九年级上
第27章 反比例函数
提示:点击 进入习题
答案显示
1
2
3
4
C
6
-2
5
C
见习题
6
7
8
9
C
6
见习题
10
8
11
见习题
答案显示
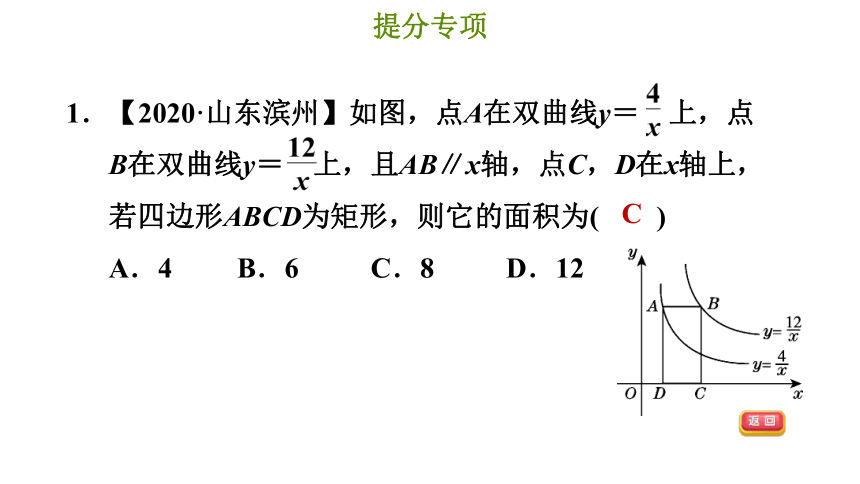
1.【2020·山东滨州】如图,点A在双曲线y= 上,点B在双曲线y= 上,且AB∥x轴,点C,D在x轴上,若四边形ABCD为矩形,则它的面积为( )
A.4 B.6 C.8 D.12
C
2.【2020·山东威海】如图,点P(m,1),点Q(-2,n)都在反比例函数y= 的图像上.过点P分别向x轴、y轴作垂线,垂足分别为点M,N.连接OP,OQ,PQ.若四边形OMPN的面积记作S1,△POQ的面积记作S2,则( )
A.S1∶S2=2∶3 B.S1∶S2=1∶1
C.S1∶S2=4∶3 D.S1∶S2=5∶3
C
3.【2020·湖南永州】如图,正比例函数y=-x与反比例函数y=- 的图像交于A,C两点,过点A作AB⊥x轴于点B,过点C作CD⊥x轴于点D,则△ABD的面积为________.
6
4.如图,在平面直角坐标系中,过原点的直线与反比例函数y=- (x<0)的图像交于点A,与反比例函数y= (k<0,x>0)的图像交于点B,过点A作x轴的垂线,过点B作y轴的垂线,两直线交于点C,若S△ABC=9,则k的值为________.
【点拨】如图,设AC交x轴于点D,BC交y轴于点E,则DO∥BE,
易得△AOD∽△ABC∽△OBE,
∵y=- ,∴S△ADO=4.
又∵S△ABC=9,∴S△ADO∶S△ABC=4∶9,∴AD∶AC=2∶3,
∴AD∶DC=2∶1,即AD∶OE=2∶1,
∴S△ADO∶S△BOE=4∶1,∴S△BOE=1,∴|k|=2S△BOE=2.
∵k<0,∴k=-2.
【答案】-2
5.【2021·河北保定安国一模改编】小亮在研究矩形的面积S与矩形的边长x,y之间的关系时,得到如下表数据:
x
0.5
1
1.5
2
3
4
6
12
y
12
6
■
3
2
1.5
1
0.5
结果发现一个数据被墨水涂黑了.
(1)被墨水涂黑的数据为_____;
(2)y与x之间的函数关系式为________________,且y随x的增大而________;
4
减小
(3)如图是小亮画出的y关于x的函数图像,点B,E均在该函数的图像上,其中矩形OABC的面积记为S1,矩形ODEF的面积记为S2,请判断S1与S2的大小关系,并说明理由;
解:S1=S2.理由如下:S1=OA·OC=k=6,S2=OD·OF=k=6,∴S1=S2.
(4)在(3)的条件下,DE交BC于点G,反比例函数y= 的图像经过点G交AB于点H,连接OG,OH,则四边形OGBH的面积为________.
4
6.【2020·辽宁营口】如图,在平面直角坐标系中,△OAB的边OA在x轴正半轴上,其中∠OAB=90°,AO=AB,点C为斜边OB的中点,反比例函数y= (k>0,x>0)的图像过点C且交线段AB于点D,连接CD,OD,若S△OCD= ,则k的值为( )
A.3 B.
C.2 D.1
【答案】C
7.【2020·江苏宿迁】如图,点A在反比例函数y= (x>0)的图像上,点B在x轴负半轴上,直线AB交y轴于点C,若 ,△AOB的面积为6,则k的值为________.
【答案】6
8.【2019·贵州安顺】如图,直线l⊥x轴于点P,且与反比例函数y1= (x>0)及y2= (x>0)的图像分别交于A,B两点,连接OA,OB,已知△OAB的面积为4,则k1-k2=________.
8
【答案】
10.如图,矩形ABOD的顶点A是一次函数y=-x-(k+1)的图像与反比例函数y= 在第二象限的图像的交点,且矩形ABOD的面积为3.
(1)求两函数的表达式;
解:由图像知k<0,由矩形ABOD的面积为3,
得|k|=3,∴k=-3.
∴反比例函数的表达式为y=- ,
一次函数的表达式为y=-x+2.
(2)求两函数图像的交点A,C的坐标;
(3)若P是y轴上一动点,且S△APC=5,求点P的坐标.
11.【2020·湖北潜江】如图,直线AB与反比例函数y= (x>0)的图像交于A,B两点,已知点A的坐标为(6,1),△AOB的面积为8.
(1)填空:反比例函数的关系式为__________;
(2)求直线AB的表达式;
解:如图,过点A作AC⊥x轴于点C,过点B作BD⊥y轴于点D,延长CA,DB交于点E,则四边形ODEC是矩形,
设B(m,n),则mn=6,
∴BE=DE-BD=6-m,AE=CE-AC=n-1,
∴S△ABE= AE·BE= (n-1)·(6-m).
∵A,B两点均在反比例函数y= (x>0)的图像上,
(3)动点P在y轴上运动,当线段PA与PB之差最大时,求点P的坐标.
解:如图,根据“三角形两边之差小于第三边”可知,当点P为直线AB与y轴的交点时,PA-PB有最大值,是AB,
把x=0代入y=- x+4,得y=4,∴P(0,4).
反比例函数中k的几何意义的应用
冀教版 九年级上
第27章 反比例函数
提示:点击 进入习题
答案显示
1
2
3
4
C
6
-2
5
C
见习题
6
7
8
9
C
6
见习题
10
8
11
见习题
答案显示
1.【2020·山东滨州】如图,点A在双曲线y= 上,点B在双曲线y= 上,且AB∥x轴,点C,D在x轴上,若四边形ABCD为矩形,则它的面积为( )
A.4 B.6 C.8 D.12
C
2.【2020·山东威海】如图,点P(m,1),点Q(-2,n)都在反比例函数y= 的图像上.过点P分别向x轴、y轴作垂线,垂足分别为点M,N.连接OP,OQ,PQ.若四边形OMPN的面积记作S1,△POQ的面积记作S2,则( )
A.S1∶S2=2∶3 B.S1∶S2=1∶1
C.S1∶S2=4∶3 D.S1∶S2=5∶3
C
3.【2020·湖南永州】如图,正比例函数y=-x与反比例函数y=- 的图像交于A,C两点,过点A作AB⊥x轴于点B,过点C作CD⊥x轴于点D,则△ABD的面积为________.
6
4.如图,在平面直角坐标系中,过原点的直线与反比例函数y=- (x<0)的图像交于点A,与反比例函数y= (k<0,x>0)的图像交于点B,过点A作x轴的垂线,过点B作y轴的垂线,两直线交于点C,若S△ABC=9,则k的值为________.
【点拨】如图,设AC交x轴于点D,BC交y轴于点E,则DO∥BE,
易得△AOD∽△ABC∽△OBE,
∵y=- ,∴S△ADO=4.
又∵S△ABC=9,∴S△ADO∶S△ABC=4∶9,∴AD∶AC=2∶3,
∴AD∶DC=2∶1,即AD∶OE=2∶1,
∴S△ADO∶S△BOE=4∶1,∴S△BOE=1,∴|k|=2S△BOE=2.
∵k<0,∴k=-2.
【答案】-2
5.【2021·河北保定安国一模改编】小亮在研究矩形的面积S与矩形的边长x,y之间的关系时,得到如下表数据:
x
0.5
1
1.5
2
3
4
6
12
y
12
6
■
3
2
1.5
1
0.5
结果发现一个数据被墨水涂黑了.
(1)被墨水涂黑的数据为_____;
(2)y与x之间的函数关系式为________________,且y随x的增大而________;
4
减小
(3)如图是小亮画出的y关于x的函数图像,点B,E均在该函数的图像上,其中矩形OABC的面积记为S1,矩形ODEF的面积记为S2,请判断S1与S2的大小关系,并说明理由;
解:S1=S2.理由如下:S1=OA·OC=k=6,S2=OD·OF=k=6,∴S1=S2.
(4)在(3)的条件下,DE交BC于点G,反比例函数y= 的图像经过点G交AB于点H,连接OG,OH,则四边形OGBH的面积为________.
4
6.【2020·辽宁营口】如图,在平面直角坐标系中,△OAB的边OA在x轴正半轴上,其中∠OAB=90°,AO=AB,点C为斜边OB的中点,反比例函数y= (k>0,x>0)的图像过点C且交线段AB于点D,连接CD,OD,若S△OCD= ,则k的值为( )
A.3 B.
C.2 D.1
【答案】C
7.【2020·江苏宿迁】如图,点A在反比例函数y= (x>0)的图像上,点B在x轴负半轴上,直线AB交y轴于点C,若 ,△AOB的面积为6,则k的值为________.
【答案】6
8.【2019·贵州安顺】如图,直线l⊥x轴于点P,且与反比例函数y1= (x>0)及y2= (x>0)的图像分别交于A,B两点,连接OA,OB,已知△OAB的面积为4,则k1-k2=________.
8
【答案】
10.如图,矩形ABOD的顶点A是一次函数y=-x-(k+1)的图像与反比例函数y= 在第二象限的图像的交点,且矩形ABOD的面积为3.
(1)求两函数的表达式;
解:由图像知k<0,由矩形ABOD的面积为3,
得|k|=3,∴k=-3.
∴反比例函数的表达式为y=- ,
一次函数的表达式为y=-x+2.
(2)求两函数图像的交点A,C的坐标;
(3)若P是y轴上一动点,且S△APC=5,求点P的坐标.
11.【2020·湖北潜江】如图,直线AB与反比例函数y= (x>0)的图像交于A,B两点,已知点A的坐标为(6,1),△AOB的面积为8.
(1)填空:反比例函数的关系式为__________;
(2)求直线AB的表达式;
解:如图,过点A作AC⊥x轴于点C,过点B作BD⊥y轴于点D,延长CA,DB交于点E,则四边形ODEC是矩形,
设B(m,n),则mn=6,
∴BE=DE-BD=6-m,AE=CE-AC=n-1,
∴S△ABE= AE·BE= (n-1)·(6-m).
∵A,B两点均在反比例函数y= (x>0)的图像上,
(3)动点P在y轴上运动,当线段PA与PB之差最大时,求点P的坐标.
解:如图,根据“三角形两边之差小于第三边”可知,当点P为直线AB与y轴的交点时,PA-PB有最大值,是AB,
把x=0代入y=- x+4,得y=4,∴P(0,4).
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
