冀教版九年级上册数学课件 第27章 27.2.2 反比例函数的性质(共33张ppt)
文档属性
| 名称 | 冀教版九年级上册数学课件 第27章 27.2.2 反比例函数的性质(共33张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-30 22:31:24 | ||
图片预览










文档简介
27.2 反比例函数的图像和性质
第2课时 反比例函数的性质
冀教版 九年级上
第27章 反比例函数
提示:点击 进入习题
答案显示
1
2
3
4
A
D
k<2
5
A
见习题
6
7
8
9
见习题
D
D
10
C
11
12
13
14
B
答案显示
15
见习题
C
A
16
见习题
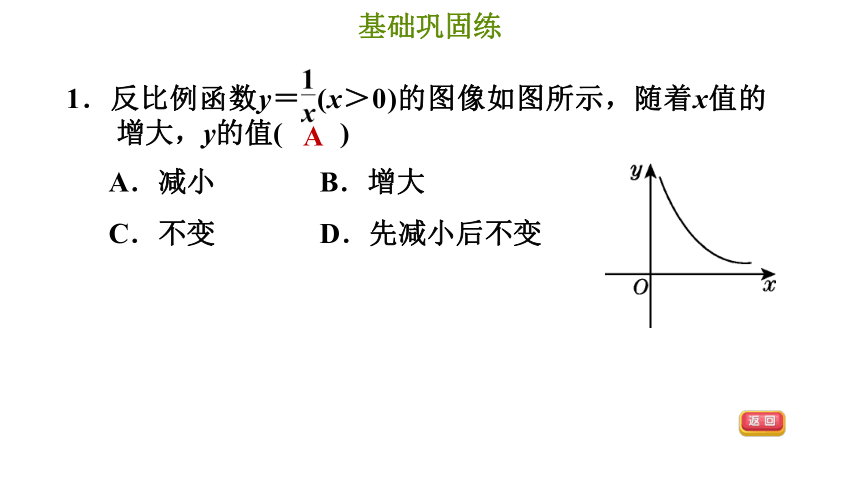
1.反比例函数y= (x>0)的图像如图所示,随着x值的增大,y的值( )
A.减小 B.增大
C.不变 D.先减小后不变
A
2.已知点A(x1,3),B(x2,6)都在反比例函数y=- 的图像上,则下列关系式一定正确的是( )
A.x1C.x2A
3.已知反比例函数y= ,下列结论中不正确的是( )
A.其图像经过点(3,1)
B.其图像分别位于第一、第三象限
C.当x>0时,y随x的增大而减小
D.当x>1时,y>3
D
···
4.【2020·河北保定二中分校期中】在双曲线y= 的每一支上,y都随着x的增大而减小,则k的取值范围为________.
k<2
6.【教材改编题】学习了反比例函数的图像和性质后,老师给同学们留了一道作业题:“已知点(-1,m)和点(2,n)都在反比例函数y= (k<0)的图像上,试比较m和n的大小.”以下是彬彬同学的解题过程:
解:∵在反比例函数y= 中,k<0, ①
∴y随x的增大而增大. ②
∵2>-1, ③
∴n>m. ④
(1)彬彬的解答过程在第几步开始出错?指出出错的原因,并给出正确的解答过程;
解:在第②步开始出错,出错的原因:在每个象限内,y随x的增大而增大,彬彬的解答忽视了“在每个象限内”这个前提.
正确解答过程如下:
∵在反比例函数y= 中,k<0,
图像在二、四象限,且在每个象限内,y随x的增大而增大.
∵点(-1,m)在第二象限的图像上,点(2,n)在第四象限的图像上,
∴m>0,n<0,∴m>n.
(2)若点(-6,p)、点(1,q)和点(3,z)也在反比例函数y= (k<0)的图像上,试比较p,q,z的大小.
解:∵ 点(-6,p)在第二象限的图像上,∴p>0.
∵点(1,q)和点(3,z) 在第四象限的图像上,y随x的增大而增大,
∴q<z<0,∴q<z<p.
7.【易错:求反比例函数中比例系数k的值时,忽视图像的位置】如图,已知A为反比例函数y= (x<0)的图像上一点,过点A作AB⊥y轴,垂足为B.若△OAB的面积为2,则k的值为( )
A.2 B.-2 C.4 D.-4
【点拨】由图像可知k<0.再根据反比例函数中k的几何意义求值即可.本题易忽略k的符号而致错.
D
8.如图,正比例函数y=kx与反比例函数y= 的图像相交于A,C两点,过点A作x轴的垂线交x轴于点B,连接BC,则△ABC的面积等于( )
A.8 B.6 C.4 D.2
C
9.【2019·河北石家庄模拟】如图,点A在反比例函数y= (x>0)的图像上,AB⊥x轴于点B,点C在x轴的负半轴上,且BO=2CO,若△ABC的面积为18,则k的值为( )
A.12 B.18 C.20 D.24
【答案】D
10.【2020·山东青岛】如图,点A是反比例函数y= (x>0)图像上的一点,AB垂直于x轴,垂足为B,△OAB的面积为6.若点P(a,7)也在此函数的图像上,则a=________.
11.【2020·湖北武汉】若点A(a-1,y1),B(a+1,y2)在反比例函数y= (k<0)的图像上,且y1>y2,则a的取值范围是( )
A.a<-1 B.-1<a<1
C.a>1 D.a<-1或a>1
【点拨】在反比例函数y= 中,
∵k<0,∴反比例函数y= 的图像位于第二、四象限,且在图像的每一支上,y随x的增大而增大,当点A(a-1,y1),B(a+1,y2)在图像的同一支上时,
∵y1>y2,∴a-1>a+1,此不等式无解;当点A(a-1,y1),B(a+1,y2)分别在图像的两支上时,
∵y1>y2,∴a-1<0,a+1>0,解得-1<a<1.
【答案】B
12.【2020·河北石家庄新华区校级一模】如图是反比例函数y= 和y=- 在x轴上方的图像,x轴的平行线AB分别与这两个函数图像相交于点A,B,与y轴交于点C,点P在x轴上,则点P从左到右的运动过程中,△APB的面积是( )
A.10 B.4
C.5 D.无法确定
【点拨】连接OA,OB.
∵x轴的平行线AB分别与这两个函数图像相交于点A,B,
∴AB⊥y轴.
∵点A,B分别在反比例函数y= 和y=- 在x轴上方的图像上,
∴S△PAB=S△AOB=S△COB+S△AOC= ×|-7|+ ×3=5,故选C.
【答案】C
13.【2020·内蒙古通辽】如图,OC交双曲线y= 于点A,且OC∶OA=5∶3,若矩形ABCD的面积是8,且AB∥x轴,则k的值是( )
A.18 B.50 C.12 D.
【点拨】如图,延长DA交x轴于E,
∵四边形ABCD是矩形,且AB∥x轴,
∴∠CAB=∠AOE,DE⊥x轴,CB⊥x轴,
∴∠AEO=∠CBA,∴△AOE∽△CAB,
【答案】A
14.【易错:由函数值的范围求自变量的取值范围时漏解】若关于x的方程 0(m是常数)有两个相等的实数根,则反比例函数y= 中,当y≤3时,x的取值范围是______________.
【点拨】本题易忽略第三象限中x<0的情况.
15.【2020·河北秦皇岛期末改编】如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在函数y= (k>0,x>0)的图像上,点D的坐标为(4,3).
(1)求k的值;
解:如图,延长AD,交x轴于点F.
∵点D的坐标为(4,3),∴DF=3,OF=4.
在Rt△DFO中,由勾股定理得OD= =5.
∵四边形ABCD是菱形,∴OD=AD=5,AD∥OB,
∴点A的坐标是(4,8),
将(4,8)代入y= ,得k=32.
(2)将点D沿x轴正方向平移得到点D′,当点D′在函数y= (k>0,x>0)的图像上时,求DD′的长.
解:由(1)可得反比例函数的表达式是y= (x>0).
∵D(4,3),将点D沿x轴正方向平移得到点D′,
∴点D′的纵坐标是3,
16.【2019·内蒙古呼和浩特】如图,在平面直角坐标系中,矩形OCAB(OC>OB)的对角线长为5,周长为14.若反比例函数y= 的图像经过矩形顶点A.
(1)求反比例函数表达式;若点(-a,y1)和(a+1,y2)在该反比例函数的图像上,试比较y1与y2的大小;
解:根据题意得OB+OC=7,OB2+OC2=52,
∵OC>OB,∴OB=3,OC=4. ∴A(3,4).
把A(3,4)的坐标代入反比例函数y= ,得m=3×4=12,
∴反比例函数表达式为y= .
∵点(-a,y1)和(a+1,y2)在反比例函数y= 的图像上,
∴-a≠0且a+1≠0,∴a≠-1且a≠0.
当a<-1时,-a>0,a+1<0,则点(-a,y1)和(a+1,y2)分别在第一象限和第三象限的反比例函数的图像上,于是有y1>y2.
当-1<a<0时,-a>0,a+1>0,
若-a>a+1,即-1<a<- ,则y1<y2;
若-a=a+1,即a=- ,则y1=y2;
若-a<a+1,即- <a<0时,y1>y2.
(2)若一次函数y=kx+b的图像过点A并与x轴交于点(-1,0),求出一次函数表达式,并直接写出kx+b- <0成立时,对应x的取值范围.
第2课时 反比例函数的性质
冀教版 九年级上
第27章 反比例函数
提示:点击 进入习题
答案显示
1
2
3
4
A
D
k<2
5
A
见习题
6
7
8
9
见习题
D
D
10
C
11
12
13
14
B
答案显示
15
见习题
C
A
16
见习题
1.反比例函数y= (x>0)的图像如图所示,随着x值的增大,y的值( )
A.减小 B.增大
C.不变 D.先减小后不变
A
2.已知点A(x1,3),B(x2,6)都在反比例函数y=- 的图像上,则下列关系式一定正确的是( )
A.x1
3.已知反比例函数y= ,下列结论中不正确的是( )
A.其图像经过点(3,1)
B.其图像分别位于第一、第三象限
C.当x>0时,y随x的增大而减小
D.当x>1时,y>3
D
···
4.【2020·河北保定二中分校期中】在双曲线y= 的每一支上,y都随着x的增大而减小,则k的取值范围为________.
k<2
6.【教材改编题】学习了反比例函数的图像和性质后,老师给同学们留了一道作业题:“已知点(-1,m)和点(2,n)都在反比例函数y= (k<0)的图像上,试比较m和n的大小.”以下是彬彬同学的解题过程:
解:∵在反比例函数y= 中,k<0, ①
∴y随x的增大而增大. ②
∵2>-1, ③
∴n>m. ④
(1)彬彬的解答过程在第几步开始出错?指出出错的原因,并给出正确的解答过程;
解:在第②步开始出错,出错的原因:在每个象限内,y随x的增大而增大,彬彬的解答忽视了“在每个象限内”这个前提.
正确解答过程如下:
∵在反比例函数y= 中,k<0,
图像在二、四象限,且在每个象限内,y随x的增大而增大.
∵点(-1,m)在第二象限的图像上,点(2,n)在第四象限的图像上,
∴m>0,n<0,∴m>n.
(2)若点(-6,p)、点(1,q)和点(3,z)也在反比例函数y= (k<0)的图像上,试比较p,q,z的大小.
解:∵ 点(-6,p)在第二象限的图像上,∴p>0.
∵点(1,q)和点(3,z) 在第四象限的图像上,y随x的增大而增大,
∴q<z<0,∴q<z<p.
7.【易错:求反比例函数中比例系数k的值时,忽视图像的位置】如图,已知A为反比例函数y= (x<0)的图像上一点,过点A作AB⊥y轴,垂足为B.若△OAB的面积为2,则k的值为( )
A.2 B.-2 C.4 D.-4
【点拨】由图像可知k<0.再根据反比例函数中k的几何意义求值即可.本题易忽略k的符号而致错.
D
8.如图,正比例函数y=kx与反比例函数y= 的图像相交于A,C两点,过点A作x轴的垂线交x轴于点B,连接BC,则△ABC的面积等于( )
A.8 B.6 C.4 D.2
C
9.【2019·河北石家庄模拟】如图,点A在反比例函数y= (x>0)的图像上,AB⊥x轴于点B,点C在x轴的负半轴上,且BO=2CO,若△ABC的面积为18,则k的值为( )
A.12 B.18 C.20 D.24
【答案】D
10.【2020·山东青岛】如图,点A是反比例函数y= (x>0)图像上的一点,AB垂直于x轴,垂足为B,△OAB的面积为6.若点P(a,7)也在此函数的图像上,则a=________.
11.【2020·湖北武汉】若点A(a-1,y1),B(a+1,y2)在反比例函数y= (k<0)的图像上,且y1>y2,则a的取值范围是( )
A.a<-1 B.-1<a<1
C.a>1 D.a<-1或a>1
【点拨】在反比例函数y= 中,
∵k<0,∴反比例函数y= 的图像位于第二、四象限,且在图像的每一支上,y随x的增大而增大,当点A(a-1,y1),B(a+1,y2)在图像的同一支上时,
∵y1>y2,∴a-1>a+1,此不等式无解;当点A(a-1,y1),B(a+1,y2)分别在图像的两支上时,
∵y1>y2,∴a-1<0,a+1>0,解得-1<a<1.
【答案】B
12.【2020·河北石家庄新华区校级一模】如图是反比例函数y= 和y=- 在x轴上方的图像,x轴的平行线AB分别与这两个函数图像相交于点A,B,与y轴交于点C,点P在x轴上,则点P从左到右的运动过程中,△APB的面积是( )
A.10 B.4
C.5 D.无法确定
【点拨】连接OA,OB.
∵x轴的平行线AB分别与这两个函数图像相交于点A,B,
∴AB⊥y轴.
∵点A,B分别在反比例函数y= 和y=- 在x轴上方的图像上,
∴S△PAB=S△AOB=S△COB+S△AOC= ×|-7|+ ×3=5,故选C.
【答案】C
13.【2020·内蒙古通辽】如图,OC交双曲线y= 于点A,且OC∶OA=5∶3,若矩形ABCD的面积是8,且AB∥x轴,则k的值是( )
A.18 B.50 C.12 D.
【点拨】如图,延长DA交x轴于E,
∵四边形ABCD是矩形,且AB∥x轴,
∴∠CAB=∠AOE,DE⊥x轴,CB⊥x轴,
∴∠AEO=∠CBA,∴△AOE∽△CAB,
【答案】A
14.【易错:由函数值的范围求自变量的取值范围时漏解】若关于x的方程 0(m是常数)有两个相等的实数根,则反比例函数y= 中,当y≤3时,x的取值范围是______________.
【点拨】本题易忽略第三象限中x<0的情况.
15.【2020·河北秦皇岛期末改编】如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在函数y= (k>0,x>0)的图像上,点D的坐标为(4,3).
(1)求k的值;
解:如图,延长AD,交x轴于点F.
∵点D的坐标为(4,3),∴DF=3,OF=4.
在Rt△DFO中,由勾股定理得OD= =5.
∵四边形ABCD是菱形,∴OD=AD=5,AD∥OB,
∴点A的坐标是(4,8),
将(4,8)代入y= ,得k=32.
(2)将点D沿x轴正方向平移得到点D′,当点D′在函数y= (k>0,x>0)的图像上时,求DD′的长.
解:由(1)可得反比例函数的表达式是y= (x>0).
∵D(4,3),将点D沿x轴正方向平移得到点D′,
∴点D′的纵坐标是3,
16.【2019·内蒙古呼和浩特】如图,在平面直角坐标系中,矩形OCAB(OC>OB)的对角线长为5,周长为14.若反比例函数y= 的图像经过矩形顶点A.
(1)求反比例函数表达式;若点(-a,y1)和(a+1,y2)在该反比例函数的图像上,试比较y1与y2的大小;
解:根据题意得OB+OC=7,OB2+OC2=52,
∵OC>OB,∴OB=3,OC=4. ∴A(3,4).
把A(3,4)的坐标代入反比例函数y= ,得m=3×4=12,
∴反比例函数表达式为y= .
∵点(-a,y1)和(a+1,y2)在反比例函数y= 的图像上,
∴-a≠0且a+1≠0,∴a≠-1且a≠0.
当a<-1时,-a>0,a+1<0,则点(-a,y1)和(a+1,y2)分别在第一象限和第三象限的反比例函数的图像上,于是有y1>y2.
当-1<a<0时,-a>0,a+1>0,
若-a>a+1,即-1<a<- ,则y1<y2;
若-a=a+1,即a=- ,则y1=y2;
若-a<a+1,即- <a<0时,y1>y2.
(2)若一次函数y=kx+b的图像过点A并与x轴交于点(-1,0),求出一次函数表达式,并直接写出kx+b- <0成立时,对应x的取值范围.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
