冀教版九年级上册数学课件 第27章 27.2.1 反比例函数的图像(共30张ppt)
文档属性
| 名称 | 冀教版九年级上册数学课件 第27章 27.2.1 反比例函数的图像(共30张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-30 00:00:00 | ||
图片预览









文档简介
27.2 反比例函数的图像和性质
第1课时 反比例函数的图像
冀教版 九年级上
第27章 反比例函数
提示:点击 进入习题
答案显示
1
2
3
4
B
A
B
5
B
见习题
6
7
8
9
D
B
见习题
10
D
C
11
12
13
14
见习题
答案显示
15
见习题
见习题
见习题
1.【2020·河北唐山乐亭期末】如果反比例函数y= (a是常数)的图像在第二、四象限,那么a的取值范围是( )
A.a>2 B.a<2 C.a>0 D.a<0
B
2.【教材改编题】如图是一个反比例函数的图像,它的表达式可能是( )
A.y=x B.y=-
C.y= x D.y=
B
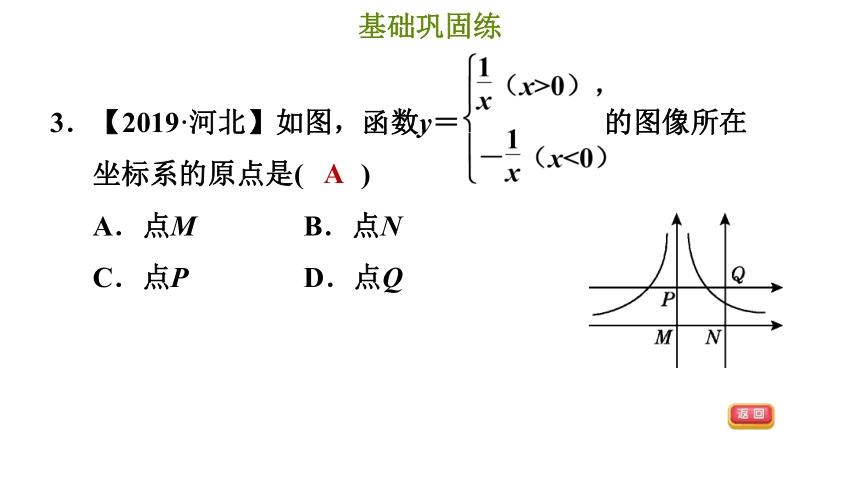
3.【2019·河北】如图,函数y= 的图像所在坐标系的原点是( )
A.点M B.点N
C.点P D.点Q
A
4.反比例函数y=(a-1)xa的图像在( )
A.第一、三象限 B.第二、四象限
C.第一、二象限 D.第三、四象限
【点拨】∵函数y=(a-1)xa是反比例函数,
∴a=-1,则a-1=-2,
故此函数图像位于第二、四象限.
B
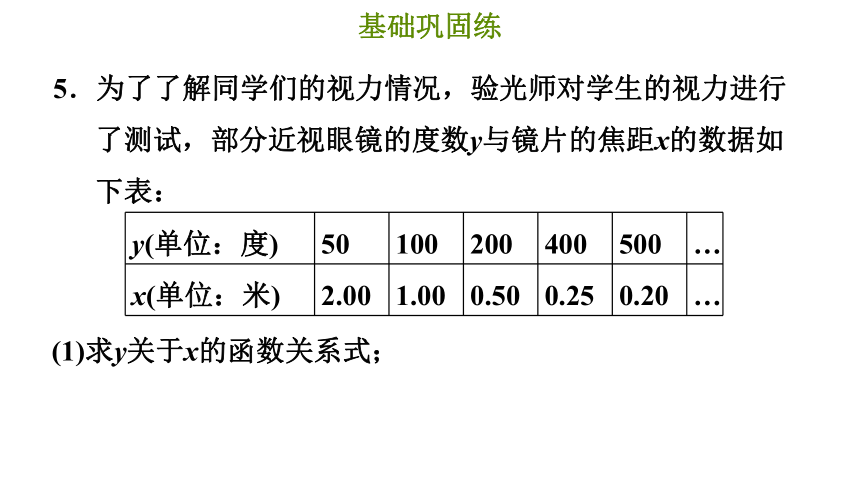
5.为了了解同学们的视力情况,验光师对学生的视力进行了测试,部分近视眼镜的度数y与镜片的焦距x的数据如下表:
y(单位:度)
50
100
200
400
500
…
x(单位:米)
2.00
1.00
0.50
0.25
0.20
…
(1)求y关于x的函数关系式;
解:图像如图所示.
(2)根据表中数据画出函数图像;
(3)某学生的视力是300度,他需要配焦距多长的镜片?
6.【2020·海南】下列各点中,在反比例函数y= 图像上的是( )
A.(-1,8) B.(-2,4)
C.(1,7) D.(2,4)
D
7.若反比例函数y= 的图像经过点(3,-2),则k的值为( )
A.-6 B.3
C.6 D.-3
【点拨】本题易误认为k=xy=-6而错选A.依题意,得x=3时,y=-2,所以-k-3=xy=-6,所以k=3.故选B.
B
8.【易错:只考虑反比例函数的图像的一个分支而错解】如图,反比例函数y= 的图像经过点A(2,1),若y≤1,则x的取值范围为( )
A.0<x≤1 B.x≥2
C.x<0或0<x≤1 D.x<0或x≥2
【点拨】本题易因只考虑第一象限中的图像而错选B.
D
(1)求m的值;
(3)上述函数图像的两个分支是否成中心对称?若是,请写出对称中心的坐标;若不是,请说明理由.
解:成中心对称,对称中心是原点(0,0).
10.如图,⊙O的半径为2,双曲线的表达式分别为y=和y=- ,则阴影部分的面积是( )
A.4π B.3π C.2π D.π
C
11.【2020·河北秦皇岛卢龙期末】若一个反比例函数的图像经过点A(m,m)和B(2m,-1),则这个反比例函数的表达式为______________.
12.【创新考法】【2020·河北】如图是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作Tm(m为1~8的整数).函数y= (x<0)的图像为曲线L.
(1)若L过点T1,则k=________;
【点拨】∵每个台阶的高和宽分别是1和2,
∴T1(-16,1),T2(-14,2),T3(-12,3),
T4(-10,4),T5(-8,5),T6(-6,6),T7(-4,7),T8(-2,8),∵L过点T1,∴k=-16×1=-16.
-16
(2)若L过点T4,则它必定还过另一点Tm,则m=________;
5
【点拨】曲线L过点T1(-16,1),T8(-2,8)时,k=-16,
曲线L过点T2(-14,2),T7(-4,7)时,k=-28,
曲线L过点T3(-12,3),T6(-6,6)时,k=-36,
曲线L过点T4(-10,4),T5(-8,5)时,k=-40,
∵曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,
(3)若曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,则k的整数值有________个.
∴-36<k<-28,
∴整数k可以取-35,-34,-33,-32,-31,-30,-29,共7个.
【答案】7
13.【2020·河北邢台任县期末】如图,矩形ABCD的顶点A,C在反比例函数y= (k>0,x>0)的图像上,若点A的坐标为(3,4),AB=2,AD∥x轴,试求点C的坐标.
解:∵四边形ABCD是矩形,
∴AD∥BC,AB⊥BC.
又∵AD∥x轴,
∴点A和点B的横坐标相同,点B和点C的纵坐标相同.
∵点A的坐标为(3,4),AB=2,
∴点B的坐标为(3,2).
∴点C的纵坐标为2,
设点C(x,2),
∵点A,C在反比例函数y= (k>0,x>0)的图像上,
∴2x=3×4,解得x=6.
∴点C的坐标为(6,2).
14.【2019·河北承德宽城月考】如图,?ABCD水平放置在平面直角坐标系中,点A,D的坐标分别为(-2,5),(0,1),点B(3,5)在函数y= (x>0)的图像上.
(1)求函数y=的表达式;
(2)求点C的坐标;
解:∵四边形ABCD为平行四边形,
∴AB=CD,AB∥CD,
∵点A,D,B的坐标分别为(-2,5),(0,1),(3,5),
∴AB=3+2=5,∴CD=5,
∴点C的坐标为(5,1).
(3)将?ABCD沿x轴正方向平移10个单位后,判断点C能否落在函数y= (x>0)的图像上,请说明理由.
15.【2019·河北保定定兴模拟】如图,在平面直角坐标系中,反比例函数y= (x>0)的图像与边长是6的正方形OABC的两边AB,BC分别相交于M,N两点.
(1)若点M是AB边的中点,求反比例函数y= (x>0)的表达式和点N的坐标;
解:∵四边形OABC是正方形,
∴OA=AB=BC=CO=6.
∵M是AB的中点,∴AM=BM=3,∴M(6,3).
解:∵AM=2,∴M(6,2).∴k=6×2=12,
(2)若AM=2,求直线MN的表达式及△OMN的面积.
∴直线MN的表达式为y=-x+8.
S△OMN=S正方形OABC-S△OAM-S△OCN-S△BMN
=6×6- ×6×2- ×6×2- ×(6-2)×(6-2)
=36-6-6-8
=16.
第1课时 反比例函数的图像
冀教版 九年级上
第27章 反比例函数
提示:点击 进入习题
答案显示
1
2
3
4
B
A
B
5
B
见习题
6
7
8
9
D
B
见习题
10
D
C
11
12
13
14
见习题
答案显示
15
见习题
见习题
见习题
1.【2020·河北唐山乐亭期末】如果反比例函数y= (a是常数)的图像在第二、四象限,那么a的取值范围是( )
A.a>2 B.a<2 C.a>0 D.a<0
B
2.【教材改编题】如图是一个反比例函数的图像,它的表达式可能是( )
A.y=x B.y=-
C.y= x D.y=
B
3.【2019·河北】如图,函数y= 的图像所在坐标系的原点是( )
A.点M B.点N
C.点P D.点Q
A
4.反比例函数y=(a-1)xa的图像在( )
A.第一、三象限 B.第二、四象限
C.第一、二象限 D.第三、四象限
【点拨】∵函数y=(a-1)xa是反比例函数,
∴a=-1,则a-1=-2,
故此函数图像位于第二、四象限.
B
5.为了了解同学们的视力情况,验光师对学生的视力进行了测试,部分近视眼镜的度数y与镜片的焦距x的数据如下表:
y(单位:度)
50
100
200
400
500
…
x(单位:米)
2.00
1.00
0.50
0.25
0.20
…
(1)求y关于x的函数关系式;
解:图像如图所示.
(2)根据表中数据画出函数图像;
(3)某学生的视力是300度,他需要配焦距多长的镜片?
6.【2020·海南】下列各点中,在反比例函数y= 图像上的是( )
A.(-1,8) B.(-2,4)
C.(1,7) D.(2,4)
D
7.若反比例函数y= 的图像经过点(3,-2),则k的值为( )
A.-6 B.3
C.6 D.-3
【点拨】本题易误认为k=xy=-6而错选A.依题意,得x=3时,y=-2,所以-k-3=xy=-6,所以k=3.故选B.
B
8.【易错:只考虑反比例函数的图像的一个分支而错解】如图,反比例函数y= 的图像经过点A(2,1),若y≤1,则x的取值范围为( )
A.0<x≤1 B.x≥2
C.x<0或0<x≤1 D.x<0或x≥2
【点拨】本题易因只考虑第一象限中的图像而错选B.
D
(1)求m的值;
(3)上述函数图像的两个分支是否成中心对称?若是,请写出对称中心的坐标;若不是,请说明理由.
解:成中心对称,对称中心是原点(0,0).
10.如图,⊙O的半径为2,双曲线的表达式分别为y=和y=- ,则阴影部分的面积是( )
A.4π B.3π C.2π D.π
C
11.【2020·河北秦皇岛卢龙期末】若一个反比例函数的图像经过点A(m,m)和B(2m,-1),则这个反比例函数的表达式为______________.
12.【创新考法】【2020·河北】如图是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作Tm(m为1~8的整数).函数y= (x<0)的图像为曲线L.
(1)若L过点T1,则k=________;
【点拨】∵每个台阶的高和宽分别是1和2,
∴T1(-16,1),T2(-14,2),T3(-12,3),
T4(-10,4),T5(-8,5),T6(-6,6),T7(-4,7),T8(-2,8),∵L过点T1,∴k=-16×1=-16.
-16
(2)若L过点T4,则它必定还过另一点Tm,则m=________;
5
【点拨】曲线L过点T1(-16,1),T8(-2,8)时,k=-16,
曲线L过点T2(-14,2),T7(-4,7)时,k=-28,
曲线L过点T3(-12,3),T6(-6,6)时,k=-36,
曲线L过点T4(-10,4),T5(-8,5)时,k=-40,
∵曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,
(3)若曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,则k的整数值有________个.
∴-36<k<-28,
∴整数k可以取-35,-34,-33,-32,-31,-30,-29,共7个.
【答案】7
13.【2020·河北邢台任县期末】如图,矩形ABCD的顶点A,C在反比例函数y= (k>0,x>0)的图像上,若点A的坐标为(3,4),AB=2,AD∥x轴,试求点C的坐标.
解:∵四边形ABCD是矩形,
∴AD∥BC,AB⊥BC.
又∵AD∥x轴,
∴点A和点B的横坐标相同,点B和点C的纵坐标相同.
∵点A的坐标为(3,4),AB=2,
∴点B的坐标为(3,2).
∴点C的纵坐标为2,
设点C(x,2),
∵点A,C在反比例函数y= (k>0,x>0)的图像上,
∴2x=3×4,解得x=6.
∴点C的坐标为(6,2).
14.【2019·河北承德宽城月考】如图,?ABCD水平放置在平面直角坐标系中,点A,D的坐标分别为(-2,5),(0,1),点B(3,5)在函数y= (x>0)的图像上.
(1)求函数y=的表达式;
(2)求点C的坐标;
解:∵四边形ABCD为平行四边形,
∴AB=CD,AB∥CD,
∵点A,D,B的坐标分别为(-2,5),(0,1),(3,5),
∴AB=3+2=5,∴CD=5,
∴点C的坐标为(5,1).
(3)将?ABCD沿x轴正方向平移10个单位后,判断点C能否落在函数y= (x>0)的图像上,请说明理由.
15.【2019·河北保定定兴模拟】如图,在平面直角坐标系中,反比例函数y= (x>0)的图像与边长是6的正方形OABC的两边AB,BC分别相交于M,N两点.
(1)若点M是AB边的中点,求反比例函数y= (x>0)的表达式和点N的坐标;
解:∵四边形OABC是正方形,
∴OA=AB=BC=CO=6.
∵M是AB的中点,∴AM=BM=3,∴M(6,3).
解:∵AM=2,∴M(6,2).∴k=6×2=12,
(2)若AM=2,求直线MN的表达式及△OMN的面积.
∴直线MN的表达式为y=-x+8.
S△OMN=S正方形OABC-S△OAM-S△OCN-S△BMN
=6×6- ×6×2- ×6×2- ×(6-2)×(6-2)
=36-6-6-8
=16.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
