2020-2021学年湘教新版八年级下册数学期末练习试题(Word版有答案)
文档属性
| 名称 | 2020-2021学年湘教新版八年级下册数学期末练习试题(Word版有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 345.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-31 11:28:16 | ||
图片预览


文档简介
2020-2021学年湘教新版八年级下册数学期末练习试题
一.选择题(共8小题,满分40分,每小题5分)
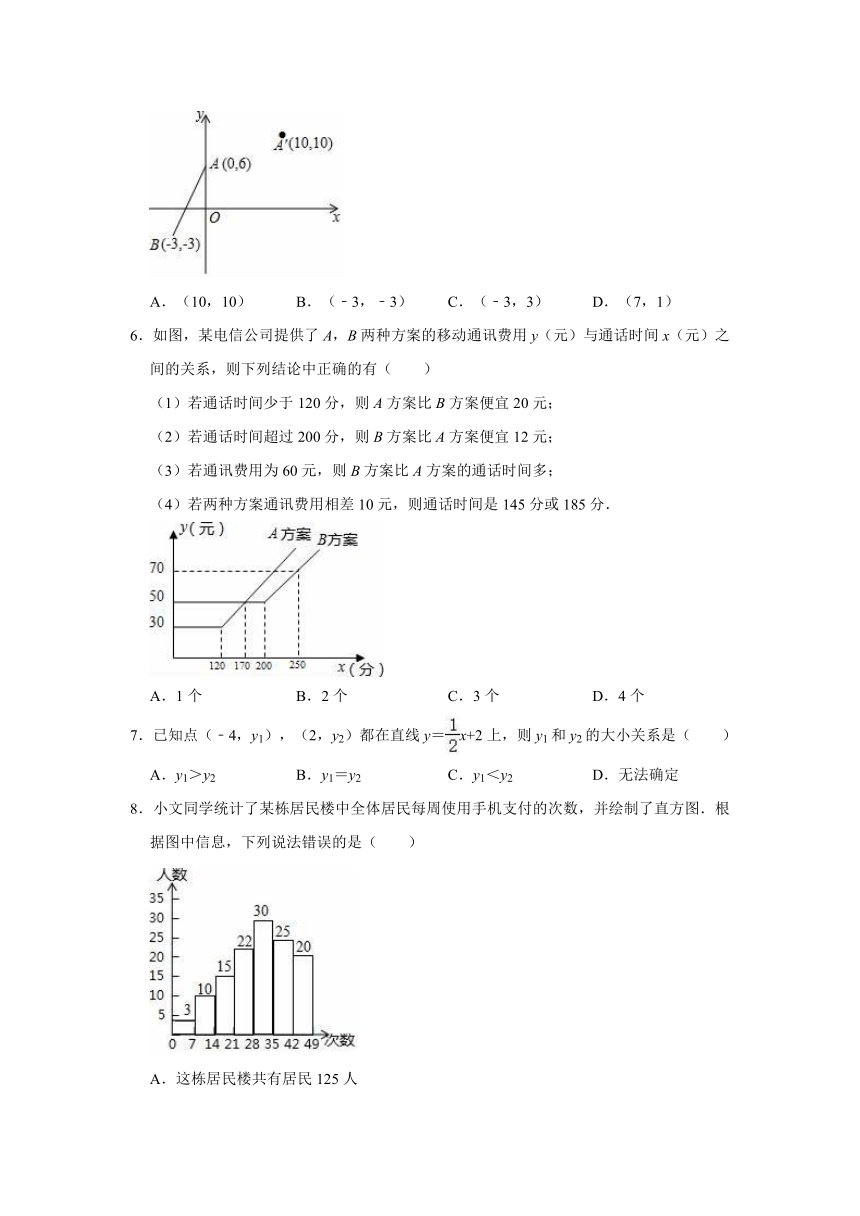
1.如图,在△ABC中,AB=10,AC=13,AD⊥BC,垂足为D,M为AD上任一点,则MC2﹣MB2等于( )
A.23
B.46
C.65
D.69
2.如图,已知点A、D、C、F在同一条直线上,AB∥DE,BC∥EF,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A.AB=DE
B.BC=EF
C.∠B=∠E
D.AD=CF
3.若一个正多边形的每一个外角都等于40°,则这个正多边形的边数是( )
A.7
B.8
C.9
D.10
4.下列图形中,是中心对称图形的是( )
A.
B.
C.
D.
5.如图,在平面直角坐标系中,点A,B的坐标分别为A(0,6),B(﹣3,﹣3).将线段AB平移后A点的对应点是A′(10,10),则点B的对应点B'的坐标为( )
A.(10,10)
B.(﹣3,﹣3)
C.(﹣3,3)
D.(7,1)
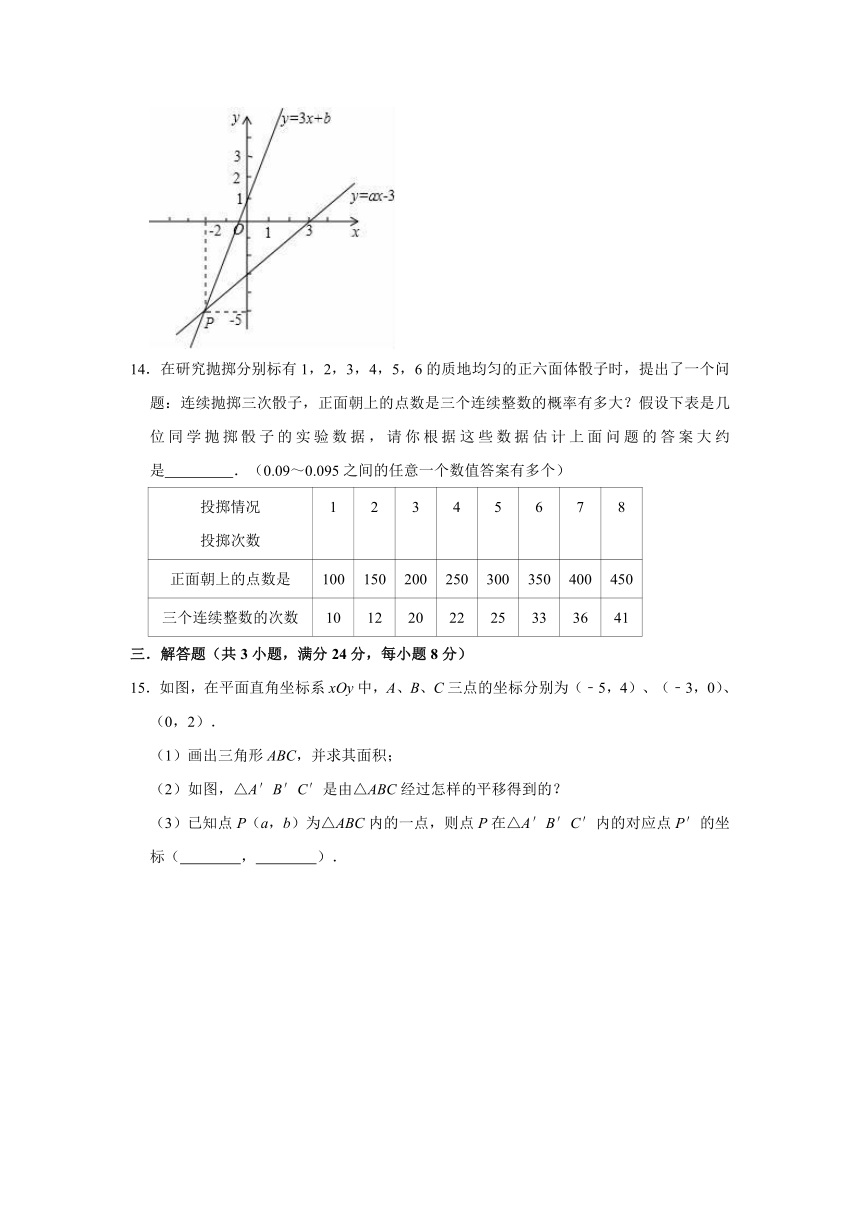
6.如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(元)之间的关系,则下列结论中正确的有( )
(1)若通话时间少于120分,则A方案比B方案便宜20元;
(2)若通话时间超过200分,则B方案比A方案便宜12元;
(3)若通讯费用为60元,则B方案比A方案的通话时间多;
(4)若两种方案通讯费用相差10元,则通话时间是145分或185分.
A.1个
B.2个
C.3个
D.4个
7.已知点(﹣4,y1),(2,y2)都在直线y=x+2上,则y1和y2的大小关系是( )
A.y1>y2
B.y1=y2
C.y1<y2
D.无法确定
8.小文同学统计了某栋居民楼中全体居民每周使用手机支付的次数,并绘制了直方图.根据图中信息,下列说法错误的是( )
A.这栋居民楼共有居民125人
B.每周使用手机支付次数为28~35次的人数最多
C.有的人每周使用手机支付的次数在35~42次
D.每周使用手机支付不超过21次的有15人
二.填空题(共6小题,满分30分,每小题5分)
9.如图,在Rt△ABC中,∠ACB=90°,D是斜边AB中点,若∠B=30°,AC=2,则CD=
.
10.如图,?ABCD中,EF为对角线BD上的两点,若添加一个条件使四边形AECF为平行四边形,则可以是:
.
11.如图所示,E是正方形ABCD边BC上任意一点,EF⊥BO于F,EG⊥CO于G,若AB=10厘米,则四边形EGOF的周长是
厘米.
12.如图,若菱形ABCD的顶点A,B的坐标分别为(6,0),(﹣4,0),点D在y轴上,则点C的坐标是
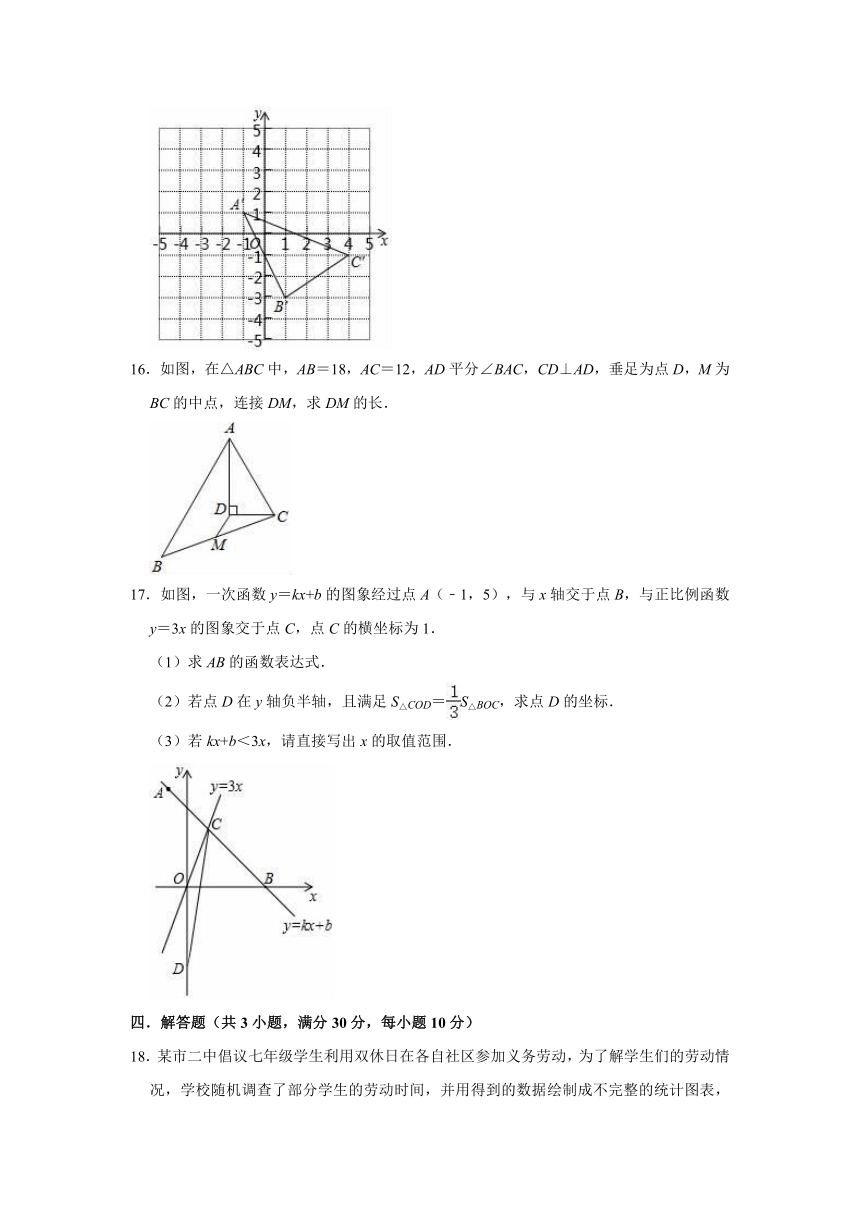
.
13.如图,已知函数y=3x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),则根据图象可得方程组的解是
.
14.在研究抛掷分别标有1,2,3,4,5,6的质地均匀的正六面体骰子时,提出了一个问题:连续抛掷三次骰子,正面朝上的点数是三个连续整数的概率有多大?假设下表是几位同学抛掷骰子的实验数据,请你根据这些数据估计上面问题的答案大约是
.(0.09~0.095之间的任意一个数值答案有多个)
投掷情况投掷次数
1
2
3
4
5
6
7
8
正面朝上的点数是
100
150
200
250
300
350
400
450
三个连续整数的次数
10
12
20
22
25
33
36
41
三.解答题(共3小题,满分24分,每小题8分)
15.如图,在平面直角坐标系xOy中,A、B、C三点的坐标分别为(﹣5,4)、(﹣3,0)、(0,2).
(1)画出三角形ABC,并求其面积;
(2)如图,△A′B′C′是由△ABC经过怎样的平移得到的?
(3)已知点P(a,b)为△ABC内的一点,则点P在△A′B′C′内的对应点P′的坐标(
,
).
16.如图,在△ABC中,AB=18,AC=12,AD平分∠BAC,CD⊥AD,垂足为点D,M为BC的中点,连接DM,求DM的长.
17.如图,一次函数y=kx+b的图象经过点A(﹣1,5),与x轴交于点B,与正比例函数y=3x的图象交于点C,点C的横坐标为1.
(1)求AB的函数表达式.
(2)若点D在y轴负半轴,且满足S△COD=S△BOC,求点D的坐标.
(3)若kx+b<3x,请直接写出x的取值范围.
四.解答题(共3小题,满分30分,每小题10分)
18.某市二中倡议七年级学生利用双休日在各自社区参加义务劳动,为了解学生们的劳动情况,学校随机调查了部分学生的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
劳动时间(时)
频数(人数)
频率
0.5
12
0.12
1
30
0.3
1.5
x
0.4
2
18
0.18
合计
m
1
(1)统计表中的x=
;
(2)被调查学生劳动时间的中位数是
;
(3)请将频数分布直方图补充完整;
(4)求所有被调查学生的平均劳动时间.
19.甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟
米,乙在A地时距地面的高度b为
米.
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式.
(3)在(2)的条件下,登山多长时间时,甲、乙两人距地面的高度差为50米?
20.如图,在?ABCD中,过点D作DE⊥AB于点E,点F在边CD上,CF=AE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)已知∠DAB=60°,AF是∠DAB的平分线,若AD=4,求?ABCD的面积.
五.解答题(共1小题,满分10分,每小题10分)
21.直线y=x﹣6与x轴、y轴分别交于点A、B,点E从B点,出发以每秒1个单位的速度沿线段BO向O点移动(与B、O点不重合),过E作EF∥AB,交x轴于F.将四边形ABEF沿EF折叠,得到四边形DCEF,设点E的运动时间为t秒.
(1)①直线y=x﹣6与坐标轴交点坐标是A(
,
),B(
,
);
②画出t=2时,四边形ABEF沿EF折叠后的图形(不写画法);
(2)若CD交y轴于H点,求证:四边形DHEF为平行四边形;并求t为何值时,四边形DHEF为菱形(计算结果不需化简);
(3)连接AD,BC,四边形ABCD是什么图形,并求t为何值时,四边形ABCD的面积为36?
六.解答题(共1小题,满分14分,每小题14分)
22.如图,四边形ABCD中,AD∥BC,∠A=∠D=90°,点E是AD的中点,连接BE,将△ABE沿BE折叠后得到△GBE,且点G在四边形ABCD内部,延长BG交DC于点F,连接EF.
(1)求证:△EGF≌△EDF;
(2)求证:BG=CD;
(3)若点F是CD的中点,BC=8,求CD的长.
参考答案与试题解析
一.选择题(共8小题,满分40分,每小题5分)
1.解:在Rt△ABD和Rt△ADC中,
BD2=AB2﹣AD2,CD2=AC2﹣AD2,
在Rt△BDM和Rt△CDM中,
BM2=BD2+MD2=AB2﹣AD2+MD2,MC2=CD2+MD2=AC2﹣AD2+MD2,
∴MC2﹣MB2
=(AC2﹣AD2+MD2)﹣(AB2﹣AD2+MD2)
=AC2﹣AB2
=132﹣102
=69.
故选:D.
2.解:A、添加AB=DE可用AAS进行判定,故本选项错误;
B、添加BC=EF可用AAS进行判定,故本选项错误;
C、添加∠B=∠E不能判定△ABC≌△DEF,故本选项正确;
D、添加AD=CF,得出AC=DF,然后可用ASA进行判定,故本选项错误;
故选:C.
3.解:∵360÷40=9,
∴这个多边形的边数是9.
故选:C.
4.解:A、不是中心对称图形,故本选项不符合题意;
B、不是中心对称图形,故本选项不符合题意;
C、是中心对称图形,故本选项符合题意;
D、不是中心对称图形,故本选项不符合题意.
故选:C.
5.解:∵点A(0,6)向右平移10个单位,向上平移4个单位得到A′(10,10),
∴点B(﹣3,﹣3)向右平移10个单位,向上平移4个单位得到B′(7,1),
故选:D.
6.解:依题意得
A:(1)当0≤x≤120,yA=30,
(2)当x>120,yA=30+(x﹣120)×[(50﹣30)÷(170﹣120)]=0.4x﹣18;
B:(1)当0≤x<200,yB=50,
当x>200,yB=50+[(70﹣50)÷(250﹣200)](x﹣200)=0.4x﹣30,
所以当x≤120时,A方案比B方案便宜20元,故(1)正确;
当x≥200时,B方案比A方案便宜12元,故(2)正确;
当y=60时,A:60=0.4x﹣18,∴x=195,
B:60=0.4x﹣30,∴x=225,故(3)正确;
当B方案为50元,A方案是40元或者60元时,两种方案通讯费用相差10元,
将yA=40或60代入,得x=145分或195分,故(4)错误;
故选:C.
7.解:∵点(﹣4,y1),(2,y2)都在直线y=x+2上,
∴y1=×(﹣4)+2=﹣2+2=0,y2=×2+2=1+2=3,
∵0<3,
∴y1<y2.
故选:C.
8.解:A、这栋居民楼共有居民3+10+15+22+30+25+20=125(人),此结论正确;
B、每周使用手机支付次数为28~35次的人数最多,这是因为从直方图上可以看出,每周使用手机支付次数为28~35次的小矩形的高度最高,所以每周使用手机支付次数为28~35次的人数最多,此结论正确,;
C、有的人每周使用手机支付的次数在35~42次,此结论正确;
D.每周使用手机支付不超过21次的有3+10+15=28人,此结论错误;
故选:D.
二.填空题(共6小题,满分30分,每小题5分)
9.解:∵∠ACB=90°,∠B=30°,AC=2,
∴AB=4,
∵D是斜边AB中点,
∴CD=AB=2,
故答案为:2.
10.解:可以是BE=DF.
理由:在平行四边形ABCD中,则可得AD∥BC,且AD=BC,
∴∠ADB=∠CBD,
∴△ADF≌△CBE,
∴CE=AF,
同理可得AE=CF,
∴四边形AECF是平行四边形.
补充其他条件只要使四边形AECF是平行四边形都可,答案并不唯一.
11.解:∵EF⊥BO于F,EG⊥CO,∠BAC=∠ACB=45°
∴△BFE,△CGE是等腰直角三角形
∴BF=EF,EG=GC
∴四边形EGOF的周长OF+EF+OG+CG=OB+OC=BD=10cm
故答案为10.
12.解:∵菱形ABCD的顶点A.B的坐标分别为(6,0),(﹣4,0),
∴CD∥AB,OA=6,OB=4,CD=AB=AD=10,
∴OD===8,
∴点D(0,8)
∵CD∥AB,CD=10,
∴点C(﹣10,8)
故答案为:(﹣10,8).
13.解:因为函数y=3x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),
所以方程组的解为.
故答案为.
14.解:通过8次试验,每次试验出现三个连续整数的频率分别是:0.1,0.08,0.1,0.09,0.08,0.09,0.09,0.09,据此估计,正面朝上的点数是三个连续整数的概率是0.09.
故本题答案为:0.09.
三.解答题(共3小题,满分24分,每小题8分)
15.解:(1)如图,△ABC即为所求.
S△ABC=4×5﹣×2×4﹣×2×5﹣×2×3=8;
(2)先向右平移4个单位,再向下平移3个单位.
(3)由题意P′(a+4,b﹣3).
故答案为:a+4,b﹣3.
16.解:延长CD交AB于E,
∵AD平分∠BAC,
∴∠EAD=∠CAD,
在△EAD和△CAD中,
,
∴△EAD≌△CAD(ASA),
∴CD=DE,AE=AC=12,
∴BE=AB﹣AE=6,
∵CD=DE,CM=MB,
∴DM是△CBE的中位线,
∴DM=BE=3.
17.解:(1)当x=1时,y=3x=3,
∴C(1,3),
将A
(﹣1,5),C(1,3)代入y=kx+b,得,
解得,
∴直线AB的解析式是y=﹣x+4;
(2)y=﹣x+4中,令y=0,则x=4,
∴B(4,0),
设D(0,m)(m<0),
S△BOC=×OB×|yC|==6,
S△COD=×OD?|xC|=|m|×1=﹣m,
∵S△COD=S△BOC,
∴﹣m=,
解得m=﹣4,
∴D(0,﹣4);
(3)观察图象可知,kx+b<3x,则x的取值范围是x>1.
四.解答题(共3小题,满分30分,每小题10分)
18.解:(1)调查的总人数是:12÷0.12=100(人),
则x=100×0.4=40(人),
故答案为:40;
(2)∵共有100名学生,处于中间位置的是第25和26个数的平均数,
∴被调查同学劳动时间的中位数是1.5小时;
故答案为:1.5小时;
(3)根据(1)得出的数据补图如下:
(4)所有被调查同学的平均劳动时间是:=1.32(小时).
19.解:(1)(300﹣100)÷20=10(米/分钟),
b=15÷1×2=30.
故答案为:10;30.
(2)当0≤x≤2时,y=15x;
当x>2时,y=30+10×3(x﹣2)=30x﹣30.
当y=30x﹣30=300时,x=11.
∴乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为y=.
(3)甲登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为y=10x+100(0≤x≤20).
当10x+100﹣(30x﹣30)=50时,解得:x=4;
当30x﹣30﹣(10x+100)=50时,解得:x=9;
当300﹣(10x+100)=50时,解得:x=15.
答:登山4分钟、9分钟或15分钟时,甲、乙两人距地面的高度差为50米.
20.(1)证明:∵四边形ABCD是平行四边形,
∴DC∥AB,DC=AB,
∵CF=AE,
∴CD﹣CF=AB﹣AE,
∴DF=BE且DC∥AB,
∴四边形BFDE是平行四边形,
又∵DE⊥AB,
∴∠DEB=90°,
∴平行四边形BFDE是矩形;
(2)解:∵∠DAB=60°,AD=4,DE⊥AB,
∴∠ADE=30°,
∴AE=AD=2,DE=AE=2,
由(1)得:四边形DFBE是矩形,
∴BF=DE=2,∠ABF=90°,
∵AF平分∠DAB,
∴∠FAB=∠DAB=30°,
∴AB=BF=×2=6,
∴?ABCD的面积=AB×DE=6×2=12.
五.解答题(共1小题,满分10分,每小题10分)
21.解:(1)①∵直线y=x﹣6与x轴、y轴分别交于点A、B,
∴y=0时,x=6;x=0时,y=﹣6;
直线y=x﹣6与坐标轴交点坐标是:A(6,0),B(0,﹣6);
故答案为:6,0;0,﹣6;
②如图1,四边形DCEF即为四边形ABEF沿EF折叠后的图形;
(2)∵四边形DCEF与四边形ABEF关于直线EF对称,AB∥EF,
∴CD∥EF.∠DFE=∠AFE,
∵OA=OB,∠AOB=90°,
∴∠BAO=45°.
∵AB∥EF,
∴∠AFE=135°.
∴∠DFE=∠AFE=135°.
∴∠AFD=360°﹣2×135°=90°,
即DF⊥x轴.
∴DF∥EH,
∴四边形DHEF为平行四边形.
要使四边形DHEF为菱形,只需EF=DF,
∵AB∥EF,∠FAB=∠EBA,
∴FA=EB,
∴DF=FA=EB=t.
又∵OE=OF=6﹣t,
∴.
∴.
∴.
∴当(秒)时,四边形DHEF为菱形.
(3)如图3,四边形ABCD是矩形;t为3秒时,四边形ABCD的面积为36.理由如下:
由折叠的性质得:AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∵∠BCE=∠EBC=∠OBA=45°,
∴∠CBA=90°,
∴四边形ABCD是矩形,
∵OA=OB=6,CE=BE=t,
∴AB=OA=6,BC=CE=t,
∴矩形ABCD的面积=AB×BC=6×t=36,
∴t=3,
即四边形ABCD是矩形,t为3秒时,四边形ABCD的面积为36.
六.解答题(共1小题,满分14分,每小题14分)
22.(1)证明:∵将△ABE沿BE折叠后得到△GBE,
∴△ABE≌△GBE,
∴∠BGE=∠A,AE=GE,
∵∠A=∠D=90°,
∴∠EGF=∠D=90°,
∵EA=ED,
∴EG=ED,
在Rt△EGF和Rt△EDF中,
,
∴Rt△EGF≌Rt△EDF(HL);
(2)证明:由折叠性质可得,AB=BG,
∵AD∥BC,∠A=∠D=90°,
∴四边形ABCD是矩形,
∴AB=CD,
∴BG=DC.
(3)解:由折叠可知AB=GB,
由(1)知Rt△EGF≌Rt△EDF,
∴GF=DF,
又∵∠C=90°,AB=CD,FD=CF,
∴GB=2GF,BF+GF=3GF,
∵BF2=BC2+CF2,
∴(3GF)2=64+GF2,
∴GF=2,
∴CD=2GF=4.
一.选择题(共8小题,满分40分,每小题5分)
1.如图,在△ABC中,AB=10,AC=13,AD⊥BC,垂足为D,M为AD上任一点,则MC2﹣MB2等于( )
A.23
B.46
C.65
D.69
2.如图,已知点A、D、C、F在同一条直线上,AB∥DE,BC∥EF,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A.AB=DE
B.BC=EF
C.∠B=∠E
D.AD=CF
3.若一个正多边形的每一个外角都等于40°,则这个正多边形的边数是( )
A.7
B.8
C.9
D.10
4.下列图形中,是中心对称图形的是( )
A.
B.
C.
D.
5.如图,在平面直角坐标系中,点A,B的坐标分别为A(0,6),B(﹣3,﹣3).将线段AB平移后A点的对应点是A′(10,10),则点B的对应点B'的坐标为( )
A.(10,10)
B.(﹣3,﹣3)
C.(﹣3,3)
D.(7,1)
6.如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(元)之间的关系,则下列结论中正确的有( )
(1)若通话时间少于120分,则A方案比B方案便宜20元;
(2)若通话时间超过200分,则B方案比A方案便宜12元;
(3)若通讯费用为60元,则B方案比A方案的通话时间多;
(4)若两种方案通讯费用相差10元,则通话时间是145分或185分.
A.1个
B.2个
C.3个
D.4个
7.已知点(﹣4,y1),(2,y2)都在直线y=x+2上,则y1和y2的大小关系是( )
A.y1>y2
B.y1=y2
C.y1<y2
D.无法确定
8.小文同学统计了某栋居民楼中全体居民每周使用手机支付的次数,并绘制了直方图.根据图中信息,下列说法错误的是( )
A.这栋居民楼共有居民125人
B.每周使用手机支付次数为28~35次的人数最多
C.有的人每周使用手机支付的次数在35~42次
D.每周使用手机支付不超过21次的有15人
二.填空题(共6小题,满分30分,每小题5分)
9.如图,在Rt△ABC中,∠ACB=90°,D是斜边AB中点,若∠B=30°,AC=2,则CD=
.
10.如图,?ABCD中,EF为对角线BD上的两点,若添加一个条件使四边形AECF为平行四边形,则可以是:
.
11.如图所示,E是正方形ABCD边BC上任意一点,EF⊥BO于F,EG⊥CO于G,若AB=10厘米,则四边形EGOF的周长是
厘米.
12.如图,若菱形ABCD的顶点A,B的坐标分别为(6,0),(﹣4,0),点D在y轴上,则点C的坐标是
.
13.如图,已知函数y=3x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),则根据图象可得方程组的解是
.
14.在研究抛掷分别标有1,2,3,4,5,6的质地均匀的正六面体骰子时,提出了一个问题:连续抛掷三次骰子,正面朝上的点数是三个连续整数的概率有多大?假设下表是几位同学抛掷骰子的实验数据,请你根据这些数据估计上面问题的答案大约是
.(0.09~0.095之间的任意一个数值答案有多个)
投掷情况投掷次数
1
2
3
4
5
6
7
8
正面朝上的点数是
100
150
200
250
300
350
400
450
三个连续整数的次数
10
12
20
22
25
33
36
41
三.解答题(共3小题,满分24分,每小题8分)
15.如图,在平面直角坐标系xOy中,A、B、C三点的坐标分别为(﹣5,4)、(﹣3,0)、(0,2).
(1)画出三角形ABC,并求其面积;
(2)如图,△A′B′C′是由△ABC经过怎样的平移得到的?
(3)已知点P(a,b)为△ABC内的一点,则点P在△A′B′C′内的对应点P′的坐标(
,
).
16.如图,在△ABC中,AB=18,AC=12,AD平分∠BAC,CD⊥AD,垂足为点D,M为BC的中点,连接DM,求DM的长.
17.如图,一次函数y=kx+b的图象经过点A(﹣1,5),与x轴交于点B,与正比例函数y=3x的图象交于点C,点C的横坐标为1.
(1)求AB的函数表达式.
(2)若点D在y轴负半轴,且满足S△COD=S△BOC,求点D的坐标.
(3)若kx+b<3x,请直接写出x的取值范围.
四.解答题(共3小题,满分30分,每小题10分)
18.某市二中倡议七年级学生利用双休日在各自社区参加义务劳动,为了解学生们的劳动情况,学校随机调查了部分学生的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
劳动时间(时)
频数(人数)
频率
0.5
12
0.12
1
30
0.3
1.5
x
0.4
2
18
0.18
合计
m
1
(1)统计表中的x=
;
(2)被调查学生劳动时间的中位数是
;
(3)请将频数分布直方图补充完整;
(4)求所有被调查学生的平均劳动时间.
19.甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟
米,乙在A地时距地面的高度b为
米.
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式.
(3)在(2)的条件下,登山多长时间时,甲、乙两人距地面的高度差为50米?
20.如图,在?ABCD中,过点D作DE⊥AB于点E,点F在边CD上,CF=AE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)已知∠DAB=60°,AF是∠DAB的平分线,若AD=4,求?ABCD的面积.
五.解答题(共1小题,满分10分,每小题10分)
21.直线y=x﹣6与x轴、y轴分别交于点A、B,点E从B点,出发以每秒1个单位的速度沿线段BO向O点移动(与B、O点不重合),过E作EF∥AB,交x轴于F.将四边形ABEF沿EF折叠,得到四边形DCEF,设点E的运动时间为t秒.
(1)①直线y=x﹣6与坐标轴交点坐标是A(
,
),B(
,
);
②画出t=2时,四边形ABEF沿EF折叠后的图形(不写画法);
(2)若CD交y轴于H点,求证:四边形DHEF为平行四边形;并求t为何值时,四边形DHEF为菱形(计算结果不需化简);
(3)连接AD,BC,四边形ABCD是什么图形,并求t为何值时,四边形ABCD的面积为36?
六.解答题(共1小题,满分14分,每小题14分)
22.如图,四边形ABCD中,AD∥BC,∠A=∠D=90°,点E是AD的中点,连接BE,将△ABE沿BE折叠后得到△GBE,且点G在四边形ABCD内部,延长BG交DC于点F,连接EF.
(1)求证:△EGF≌△EDF;
(2)求证:BG=CD;
(3)若点F是CD的中点,BC=8,求CD的长.
参考答案与试题解析
一.选择题(共8小题,满分40分,每小题5分)
1.解:在Rt△ABD和Rt△ADC中,
BD2=AB2﹣AD2,CD2=AC2﹣AD2,
在Rt△BDM和Rt△CDM中,
BM2=BD2+MD2=AB2﹣AD2+MD2,MC2=CD2+MD2=AC2﹣AD2+MD2,
∴MC2﹣MB2
=(AC2﹣AD2+MD2)﹣(AB2﹣AD2+MD2)
=AC2﹣AB2
=132﹣102
=69.
故选:D.
2.解:A、添加AB=DE可用AAS进行判定,故本选项错误;
B、添加BC=EF可用AAS进行判定,故本选项错误;
C、添加∠B=∠E不能判定△ABC≌△DEF,故本选项正确;
D、添加AD=CF,得出AC=DF,然后可用ASA进行判定,故本选项错误;
故选:C.
3.解:∵360÷40=9,
∴这个多边形的边数是9.
故选:C.
4.解:A、不是中心对称图形,故本选项不符合题意;
B、不是中心对称图形,故本选项不符合题意;
C、是中心对称图形,故本选项符合题意;
D、不是中心对称图形,故本选项不符合题意.
故选:C.
5.解:∵点A(0,6)向右平移10个单位,向上平移4个单位得到A′(10,10),
∴点B(﹣3,﹣3)向右平移10个单位,向上平移4个单位得到B′(7,1),
故选:D.
6.解:依题意得
A:(1)当0≤x≤120,yA=30,
(2)当x>120,yA=30+(x﹣120)×[(50﹣30)÷(170﹣120)]=0.4x﹣18;
B:(1)当0≤x<200,yB=50,
当x>200,yB=50+[(70﹣50)÷(250﹣200)](x﹣200)=0.4x﹣30,
所以当x≤120时,A方案比B方案便宜20元,故(1)正确;
当x≥200时,B方案比A方案便宜12元,故(2)正确;
当y=60时,A:60=0.4x﹣18,∴x=195,
B:60=0.4x﹣30,∴x=225,故(3)正确;
当B方案为50元,A方案是40元或者60元时,两种方案通讯费用相差10元,
将yA=40或60代入,得x=145分或195分,故(4)错误;
故选:C.
7.解:∵点(﹣4,y1),(2,y2)都在直线y=x+2上,
∴y1=×(﹣4)+2=﹣2+2=0,y2=×2+2=1+2=3,
∵0<3,
∴y1<y2.
故选:C.
8.解:A、这栋居民楼共有居民3+10+15+22+30+25+20=125(人),此结论正确;
B、每周使用手机支付次数为28~35次的人数最多,这是因为从直方图上可以看出,每周使用手机支付次数为28~35次的小矩形的高度最高,所以每周使用手机支付次数为28~35次的人数最多,此结论正确,;
C、有的人每周使用手机支付的次数在35~42次,此结论正确;
D.每周使用手机支付不超过21次的有3+10+15=28人,此结论错误;
故选:D.
二.填空题(共6小题,满分30分,每小题5分)
9.解:∵∠ACB=90°,∠B=30°,AC=2,
∴AB=4,
∵D是斜边AB中点,
∴CD=AB=2,
故答案为:2.
10.解:可以是BE=DF.
理由:在平行四边形ABCD中,则可得AD∥BC,且AD=BC,
∴∠ADB=∠CBD,
∴△ADF≌△CBE,
∴CE=AF,
同理可得AE=CF,
∴四边形AECF是平行四边形.
补充其他条件只要使四边形AECF是平行四边形都可,答案并不唯一.
11.解:∵EF⊥BO于F,EG⊥CO,∠BAC=∠ACB=45°
∴△BFE,△CGE是等腰直角三角形
∴BF=EF,EG=GC
∴四边形EGOF的周长OF+EF+OG+CG=OB+OC=BD=10cm
故答案为10.
12.解:∵菱形ABCD的顶点A.B的坐标分别为(6,0),(﹣4,0),
∴CD∥AB,OA=6,OB=4,CD=AB=AD=10,
∴OD===8,
∴点D(0,8)
∵CD∥AB,CD=10,
∴点C(﹣10,8)
故答案为:(﹣10,8).
13.解:因为函数y=3x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),
所以方程组的解为.
故答案为.
14.解:通过8次试验,每次试验出现三个连续整数的频率分别是:0.1,0.08,0.1,0.09,0.08,0.09,0.09,0.09,据此估计,正面朝上的点数是三个连续整数的概率是0.09.
故本题答案为:0.09.
三.解答题(共3小题,满分24分,每小题8分)
15.解:(1)如图,△ABC即为所求.
S△ABC=4×5﹣×2×4﹣×2×5﹣×2×3=8;
(2)先向右平移4个单位,再向下平移3个单位.
(3)由题意P′(a+4,b﹣3).
故答案为:a+4,b﹣3.
16.解:延长CD交AB于E,
∵AD平分∠BAC,
∴∠EAD=∠CAD,
在△EAD和△CAD中,
,
∴△EAD≌△CAD(ASA),
∴CD=DE,AE=AC=12,
∴BE=AB﹣AE=6,
∵CD=DE,CM=MB,
∴DM是△CBE的中位线,
∴DM=BE=3.
17.解:(1)当x=1时,y=3x=3,
∴C(1,3),
将A
(﹣1,5),C(1,3)代入y=kx+b,得,
解得,
∴直线AB的解析式是y=﹣x+4;
(2)y=﹣x+4中,令y=0,则x=4,
∴B(4,0),
设D(0,m)(m<0),
S△BOC=×OB×|yC|==6,
S△COD=×OD?|xC|=|m|×1=﹣m,
∵S△COD=S△BOC,
∴﹣m=,
解得m=﹣4,
∴D(0,﹣4);
(3)观察图象可知,kx+b<3x,则x的取值范围是x>1.
四.解答题(共3小题,满分30分,每小题10分)
18.解:(1)调查的总人数是:12÷0.12=100(人),
则x=100×0.4=40(人),
故答案为:40;
(2)∵共有100名学生,处于中间位置的是第25和26个数的平均数,
∴被调查同学劳动时间的中位数是1.5小时;
故答案为:1.5小时;
(3)根据(1)得出的数据补图如下:
(4)所有被调查同学的平均劳动时间是:=1.32(小时).
19.解:(1)(300﹣100)÷20=10(米/分钟),
b=15÷1×2=30.
故答案为:10;30.
(2)当0≤x≤2时,y=15x;
当x>2时,y=30+10×3(x﹣2)=30x﹣30.
当y=30x﹣30=300时,x=11.
∴乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为y=.
(3)甲登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为y=10x+100(0≤x≤20).
当10x+100﹣(30x﹣30)=50时,解得:x=4;
当30x﹣30﹣(10x+100)=50时,解得:x=9;
当300﹣(10x+100)=50时,解得:x=15.
答:登山4分钟、9分钟或15分钟时,甲、乙两人距地面的高度差为50米.
20.(1)证明:∵四边形ABCD是平行四边形,
∴DC∥AB,DC=AB,
∵CF=AE,
∴CD﹣CF=AB﹣AE,
∴DF=BE且DC∥AB,
∴四边形BFDE是平行四边形,
又∵DE⊥AB,
∴∠DEB=90°,
∴平行四边形BFDE是矩形;
(2)解:∵∠DAB=60°,AD=4,DE⊥AB,
∴∠ADE=30°,
∴AE=AD=2,DE=AE=2,
由(1)得:四边形DFBE是矩形,
∴BF=DE=2,∠ABF=90°,
∵AF平分∠DAB,
∴∠FAB=∠DAB=30°,
∴AB=BF=×2=6,
∴?ABCD的面积=AB×DE=6×2=12.
五.解答题(共1小题,满分10分,每小题10分)
21.解:(1)①∵直线y=x﹣6与x轴、y轴分别交于点A、B,
∴y=0时,x=6;x=0时,y=﹣6;
直线y=x﹣6与坐标轴交点坐标是:A(6,0),B(0,﹣6);
故答案为:6,0;0,﹣6;
②如图1,四边形DCEF即为四边形ABEF沿EF折叠后的图形;
(2)∵四边形DCEF与四边形ABEF关于直线EF对称,AB∥EF,
∴CD∥EF.∠DFE=∠AFE,
∵OA=OB,∠AOB=90°,
∴∠BAO=45°.
∵AB∥EF,
∴∠AFE=135°.
∴∠DFE=∠AFE=135°.
∴∠AFD=360°﹣2×135°=90°,
即DF⊥x轴.
∴DF∥EH,
∴四边形DHEF为平行四边形.
要使四边形DHEF为菱形,只需EF=DF,
∵AB∥EF,∠FAB=∠EBA,
∴FA=EB,
∴DF=FA=EB=t.
又∵OE=OF=6﹣t,
∴.
∴.
∴.
∴当(秒)时,四边形DHEF为菱形.
(3)如图3,四边形ABCD是矩形;t为3秒时,四边形ABCD的面积为36.理由如下:
由折叠的性质得:AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∵∠BCE=∠EBC=∠OBA=45°,
∴∠CBA=90°,
∴四边形ABCD是矩形,
∵OA=OB=6,CE=BE=t,
∴AB=OA=6,BC=CE=t,
∴矩形ABCD的面积=AB×BC=6×t=36,
∴t=3,
即四边形ABCD是矩形,t为3秒时,四边形ABCD的面积为36.
六.解答题(共1小题,满分14分,每小题14分)
22.(1)证明:∵将△ABE沿BE折叠后得到△GBE,
∴△ABE≌△GBE,
∴∠BGE=∠A,AE=GE,
∵∠A=∠D=90°,
∴∠EGF=∠D=90°,
∵EA=ED,
∴EG=ED,
在Rt△EGF和Rt△EDF中,
,
∴Rt△EGF≌Rt△EDF(HL);
(2)证明:由折叠性质可得,AB=BG,
∵AD∥BC,∠A=∠D=90°,
∴四边形ABCD是矩形,
∴AB=CD,
∴BG=DC.
(3)解:由折叠可知AB=GB,
由(1)知Rt△EGF≌Rt△EDF,
∴GF=DF,
又∵∠C=90°,AB=CD,FD=CF,
∴GB=2GF,BF+GF=3GF,
∵BF2=BC2+CF2,
∴(3GF)2=64+GF2,
∴GF=2,
∴CD=2GF=4.
同课章节目录
