人教版八年级下册数学第十八章《平行四边形》单元知识测试卷(word版含答案)
文档属性
| 名称 | 人教版八年级下册数学第十八章《平行四边形》单元知识测试卷(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-31 00:00:00 | ||
图片预览



文档简介
人教版八年级下册数学第十八章《平行四边形》单元知识测试卷
一、单选题
1.下列命题中是真命题的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.对角线互相垂直且平分的四边形是菱形
C.一个角为90°且一组邻边相等的四边形是正方形
D.对角线互相垂直且相等的四边形是矩形
2.如图,下列四组条件中,不能判定四边形是平行四边形的是( )
A. B.
C. D.
3.如图的对角线与相交于点O,.若,则的长是( )
A.8 B. C.10 D.
4.如图,在矩形ABCD中,E是BC边上的点,连接AE、DE,将DEC沿线段DE翻折,点C恰好落在线段AE上的点F处.若AB=6,BE:EC=4:1,则线段DE的长为( )
A.4 B.2 C.4 D.2
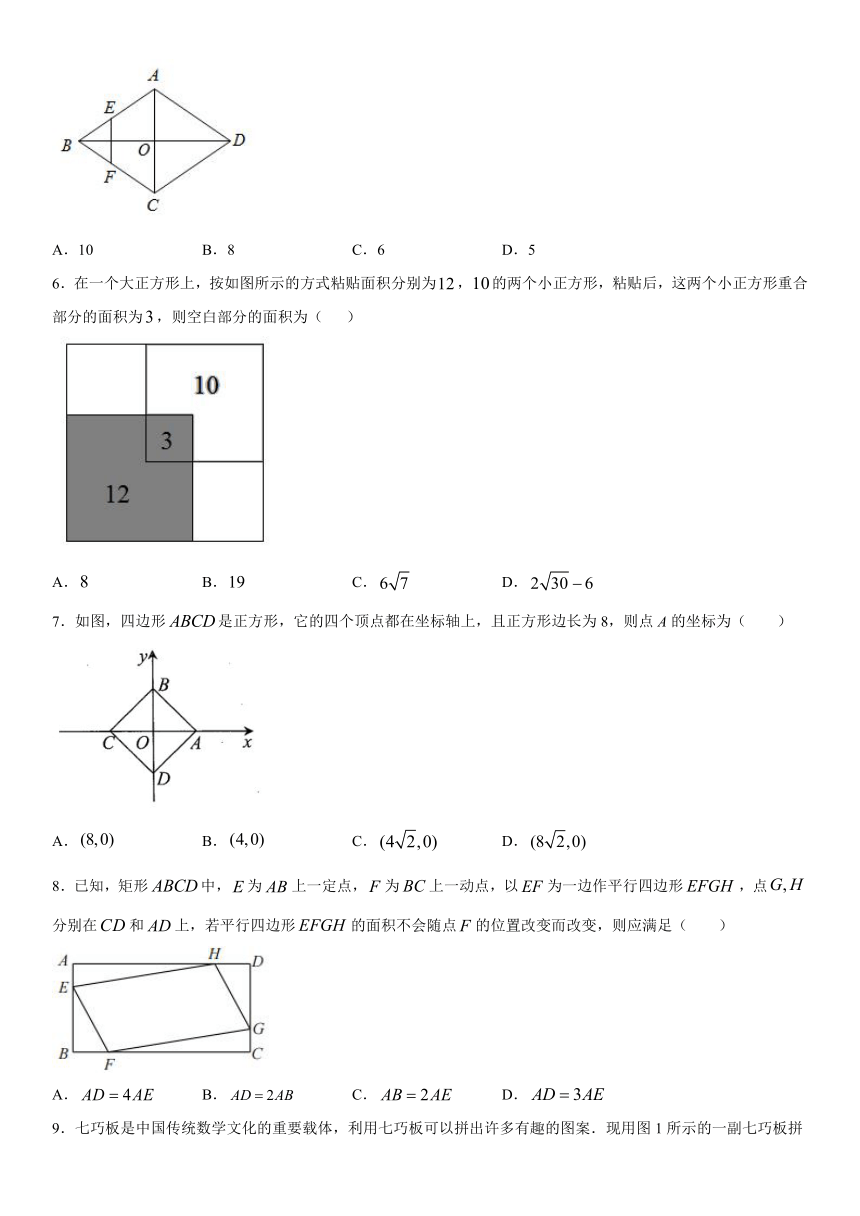
5.如图,菱形的对角线,相交于O点,E,F分别是,的中点,连接.若,则菱形的边长为( )
A.10 B.8 C.6 D.5
6.在一个大正方形上,按如图所示的方式粘贴面积分别为,的两个小正方形,粘贴后,这两个小正方形重合部分的面积为,则空白部分的面积为( )
A. B. C. D.
7.如图,四边形是正方形,它的四个顶点都在坐标轴上,且正方形边长为8,则点A的坐标为( )
A. B. C. D.
8.已知,矩形中,为上一定点,为上一动点,以为一边作平行四边形,点分别在和上,若平行四边形的面积不会随点的位置改变而改变,则应满足( )
A. B. C. D.
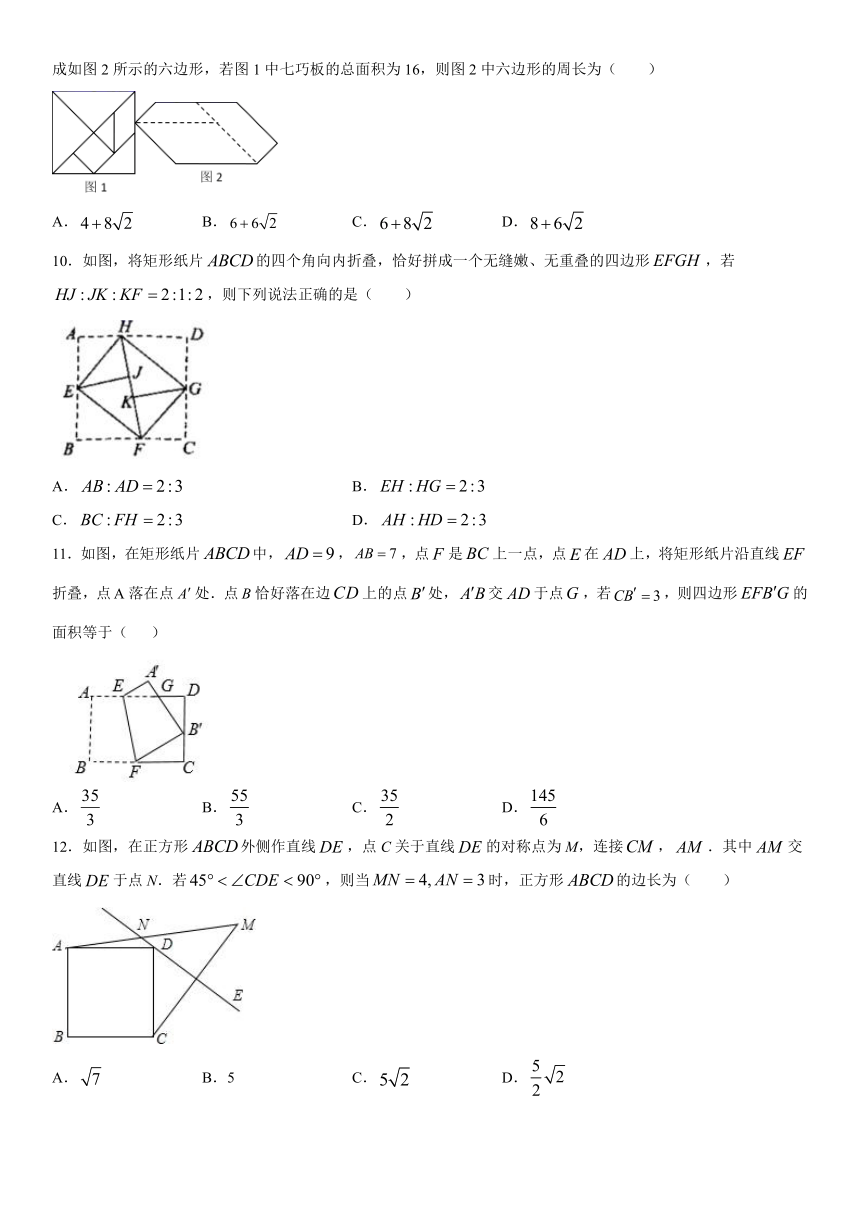
9.七巧板是中国传统数学文化的重要载体,利用七巧板可以拼出许多有趣的图案.现用图1所示的一副七巧板拼成如图2所示的六边形,若图1中七巧板的总面积为16,则图2中六边形的周长为( )
A. B. C. D.
10.如图,将矩形纸片的四个角向内折叠,恰好拼成一个无缝嫩、无重叠的四边形,若,则下列说法正确的是( )
A. B.
C. D.
11.如图,在矩形纸片中,,,点是上一点,点在上,将矩形纸片沿直线折叠,点落在点处.点恰好落在边上的点处,交于点,若,则四边形的面积等于( )
A. B. C. D.
12.如图,在正方形外侧作直线,点C关于直线的对称点为M,连接,.其中交直线于点N.若,则当时,正方形的边长为( )
A. B.5 C. D.
二、填空题
13.若顺次连接一个四边形各边中点所得的图形为矩形,则这个四边形需要满足的条件为______.
14.如图,在平行四边形中,的平分线交边于,平形四边形的周长是,,则=______.
15.如图,在中,,,,为边上一动点,于,于,连接,则的最小值为______.
16.如图,菱形ABCD和菱形EFGH的面积分别为和,CD落在EF上,,若的面积为,则的面积是____.
17.如图,平行四边形中,,,点在边上以每秒的速度从点向点运动,点在边上,以每秒的速度从点出发,在间往返运动,两个点同时出发,当点到达点时停止(同时点也停止).在运动以后,当______时以、、、四点组成的四边形为平行四边形.
三、解答题
18.已知点、分别是平行四边形的边、的中点.
(1)求证:四边形是平行四边形;
(2)若,,求平行四边形的周长.
19.如图,点为正方形对角线上一点, 于点, 于点.
(1)求证:.
(2)若正方形的边长为12,求,四边形的周长.
20.如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=4,∠AOB=60°,求矩形ABCD的面积.
21.如图,在正方形中,为射线上的动点,连接,交于.
(1)证明:;
(2)若交于,当时,求之长;
(3)是否存在点,使得为等腰三角形,若存在,请求出之长;若不存在,请说明理由.
22.问题呈现:(1)如图①,在一次数学折纸活动中,有一张矩形纸片ABCD,点E在AD上,点F在BC上,小华同学将这张矩形纸片沿EF翻折得到四边形,交AD于点H,小华认为EFH是等腰三角形,你认为小华的判断正确吗?请说明理由.
问题拓展:(2)如图②,在“问题呈现”的条件下,当点C的对应点落在AD上时,已知DE=a,CD=b,CF=c,写出a、b、c满足的数量关系,并证明你的结论.
问题应用:(3)如图③,在平行四边形ABCD中,AB=3,AD=4.将平行四边形ABCD沿对角线AC翻折得到ACE,AE交BC于点F.若点F为BC的中点,则平行四边形ABCD的面积为 .
参考答案
1.B
解:A、一组对边平行,另一组对边相等的四边形是平行四边形或等腰梯形,
本选项说法是假命题;
B、对角线互相垂直且平分的四边形是菱形,
本选项说法是真命题;
C、一个角为90°且一组邻边相等的平行四边形是正方形,
本选项说法是假命题;
D、对角线互相平分且相等的四边形是矩形,
本选项说法是假命题;
故选:B.
2.C
A.两组对边分别相等可判断四边形是平行四边形;
B.一组对边平行且相等可判断四边形是平行四边形;
C. 一组对边平行,另一组对边相等不能四边形是平行四边形;
D.两组对边分别平行可判断四边形是平行四边形;
故选C.
3.B
解:∵四边形ABCD是平行四边形,且BD=10,AC=6,
∴AO=OC=AC=3,BO=DO=BD=5,AB=CD,
又∵AB⊥AC,即∠BAC=90°,
∴AB==4,
∴CD=AB=4,
∴BC===,
故选B.
4.D
解:由矩形ABCD,得∠B=∠C=90°,CD=AB,AD=BC,AD∥BC.
由△DEC沿线段DE翻折,点C恰好落在线段AE上的点F处,得△DFE≌△DCE,
∴DF=DC,∠DFE=∠C=90°,
∴DF=AB,∠AFD=90°,
∴∠AFD=∠B,
由AD∥BC得∠DAF=∠AEB,
在△ABE与△DFA中,
,
∴△ABE≌△DFA(AAS).
∵BE:CE=4:1,
∴设CE=x,BE=4x,则AD=BC=5x,
由△ABE≌△DFA,得AF=BE=4x,
在Rt△ADF中,由勾股定理可得DF=3x,
又∵DF=CD=AB=6,
∴x=2,
在Rt△DCE中,DE===2.
故选:D.
5.D
解:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥BD,OA=AC,OB=BD=4,
∴∠AOB=90°,
∵E、F分别是AB、BC边上的中点,
∴EF是△ABC的中位线,
∴AC=2EF=6,
∴OA=3,
∴AB==5,
故选:D.
6.D
解:由图得,大正方形的边长为:,
空白部分的面积为:,
故选D.
7.C
解:四边形是正方形,
,
正方形边长为8,
点A的坐标为
故选C.
8.C
解:设AB=a,BC=b,BE=c,BF=x,
∴S平行四边形EFGH=S矩形ABCD-2(S△BEF+S△AEH)
=ab-2[cx+(a-c)(b-x)]
=ab-(cx+ab-ax-bc+cx)
=ab-cx-ab+ax+bc-cx
=(a-2c)x+bc,
∵F为BC上一动点,
∴x是变量,(a-2c)是x的系数,
∵平行四边形EFGH的面积不会随点F的位置改变而改变,为固定值,
∴x的系数为0,bc为固定值,
∴a-2c=0,
∴a=2c,
∴E是AB的中点,
∴AB=2AE,
故选:C.
9.D
∵图1的总面积为16,
∴正方形的边长为4,
∴①、②的直角边长为,斜边长为4,
④的短边长为,长边长为2,
③的直角边长为,长边长为2,
⑤为正方形,边长为,
⑥的斜边长为2,直角边长为,
⑦的直角边长为,
∴.
故选:D.
10.D
解:∵HJ:JK:KF=2:1:2,
∴设HJ=2x,JK=x,KF=2x,
由折叠的性质得:AH=HJ=2x,
DH =HK=3x,AE=EJ= BE,
∴FH=5x,
∴AH:HD=2:3,
故D说法正确;
故选:D.
11.D
解:∵四边形ABCD是矩形,且
∴
∵
∴
设
∴
∵且
∴
∴
∴
∵∠
∴∠,
∴
∵
∴
∴
∴
∵
∴
设
∴
又
∴
解得,
∴
∵,
∴四边形的面积
故选:D
12.D
解:如图所示,连接、、,
∵点C关于直线的对称点为M,
∴CN=MN,CD=DM,
∴∠NCM=∠NMC,∠DCM=∠DMC,
∴,
在正方形中,,
∴,
∴,
∴,
∵,
∴,
∴是直角三角形,
∴,
∴正方形的边长.
故选:D.
13.对角线互相垂直
解:若一个四边形对角线互相垂直,则顺次连接这个四边形各边中点所得的图形为矩形,
理由如下:∵E,F,G,H分别是AB,BC,CD,DA的中点,
∴EH∥BD,FG∥BD,
∴EH∥FG,
同理,EF∥HG,
∴四边形EFGH是平行四边形,
∵AC⊥BD,
∴EH⊥EF,
∴四边形EFGH是矩形.
故答案为:对角线互相垂直.
14.3
解:四边形是平行四边形,
,,,
,
平行四边形的周长是16,
,
是的平分线,
,
,
,
,
,
,
故答案为:3.
15.
解:,,,
,
为直角三角形,,
于,于,
,
四边形为矩形,
连接,如图,,当的值最小时,的值最小,
当时,的值最小,
根据面积公式,,
,
的最小值为.
故答案为:.
16.8.5
解:连接FH,在菱形和菱形中,,
,
,
,
和同底等高,
菱形的面积为,,
,
,
故答案为:8.5.
17.4.8s或8s或9.6s
解:设经过t秒,以点P、D、Q、B为顶点组成平行四边形,
∵以点P、D、Q、B为顶点组成平行四边形,
∴DP=BQ,
分为以下情况:①点Q的运动路线是C-B,方程为12-4t=12-t,
此时方程t=0,此时不符合题意;
②点Q的运动路线是C-B-C,方程为4t-12=12-t,
解得:t=4.8;
③点Q的运动路线是C-B-C-B,方程为12-(4t-24)=12-t,
解得:t=8;
④点Q的运动路线是C-B-C-B-C,方程为4t-36=12-t,
解得:t=9.6;
综上所述,t=4.8s或8s或9.6s时,以P、D、Q、B四点组成的四边形为平行四边形,
故答案为:4.8s或8s或9.6s.
18.
解:(1)证明:四边形是平行四边形,
,,
点、分别是的边、的中点,
,,
,,
四边形是平行四边形;
(2),,是的中点.
,
四边形是菱形,
的周长.
19.
(1)证明:连接PC,
∵四边形ABCD是正方形,
∴AB=CB,∠ABD=∠CBD=45°,∠BCD=90°,
在△ABP与△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PE⊥CD,PF⊥BC,
∴∠PFC=90°,∠PEC=90°.
又∵∠BCD=90°,
∴四边形PFCE是矩形,
∴EF=PC,
∴PA=EF;
(2)由(1)知四边形PFCE是矩形,
∴PE=CF,PF=CE,
又∵∠CBD=45°,∠PEB=90°,
∴BE=PE,
又∵BC=12,
∴矩形PFCE的周长为2(PE+EC)=2(BE+EC)=2BC=24.
20.(
(1)证明:∵四边形ABCD是矩形,
∴OA=OC,OB=OD,AC=BD,∠ABC=90°,
∵BE=DF,
∴OE=OF,
在△AOE和△COF中,
,
∴△AOE≌△COF(SAS),
∴AE=CF;
(2)解:∵OA=OC,OB=OD,AC=BD,
∴OA=OB,
∵∠AOB=∠COD=60°,
∴△AOB是等边三角形,
∴OA=AB=4,
∴AC=2OA=8,
在Rt△ABC中,,
∴矩形ABCD的面积=AB?BC=4×4=16.
21.
解:(1)证明:四边形是正方形,
,,
在和中,
,
;
(2)如图1,
,
,
,
,
,
,
,
,
,
,,
,
,
;
(3)当时,
,
,即,
点与点重合,
;
当时,
,
,
是的一个锐角,
,
不存在;
当时,
,
,
如图2,在上截取,连接,
,,
,
,
,
,
,
综上所述:或.
22.
解:(1)小华的判断是正确的.
在矩形ABCD中, AD∥BC,∴∠HEF=∠EFC.
由折叠,得∠HFE=∠EFC,
∴∠HFE=∠HEF
∴HE=HF
∴△EFH是等腰三角形
(2).
在矩形ABCD中,∠D=90°,
由折叠,得,,,,
由问题呈现,得.
在Rt△中,,
∴.
(3)∵四边形ABCD为平行四边形,AB=3,AD=4,
∴CD=3,BC=4,∠B=∠D,
由折叠性质可知,EC=CD,AE=AD=4,∠E=∠D,
∴EC=AB,∠B=∠E,
∵点F为BC的中点,
∴BF=CF,
∵∠AFB=∠EFC,
∴△AFB≌△EFC(AAS),
∴AF=FE=AE=×4=2.
∴BF=AF=2,
如图,过点F作FH⊥AB于H,
则AH=BH=AB=×3=,
在Rt△BHF中,HF=,
∴S△ABF=AB?HF=×3×=,
∴S?ABCD=4S△ABF=4×=.
故答案为:
一、单选题
1.下列命题中是真命题的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.对角线互相垂直且平分的四边形是菱形
C.一个角为90°且一组邻边相等的四边形是正方形
D.对角线互相垂直且相等的四边形是矩形
2.如图,下列四组条件中,不能判定四边形是平行四边形的是( )
A. B.
C. D.
3.如图的对角线与相交于点O,.若,则的长是( )
A.8 B. C.10 D.
4.如图,在矩形ABCD中,E是BC边上的点,连接AE、DE,将DEC沿线段DE翻折,点C恰好落在线段AE上的点F处.若AB=6,BE:EC=4:1,则线段DE的长为( )
A.4 B.2 C.4 D.2
5.如图,菱形的对角线,相交于O点,E,F分别是,的中点,连接.若,则菱形的边长为( )
A.10 B.8 C.6 D.5
6.在一个大正方形上,按如图所示的方式粘贴面积分别为,的两个小正方形,粘贴后,这两个小正方形重合部分的面积为,则空白部分的面积为( )
A. B. C. D.
7.如图,四边形是正方形,它的四个顶点都在坐标轴上,且正方形边长为8,则点A的坐标为( )
A. B. C. D.
8.已知,矩形中,为上一定点,为上一动点,以为一边作平行四边形,点分别在和上,若平行四边形的面积不会随点的位置改变而改变,则应满足( )
A. B. C. D.
9.七巧板是中国传统数学文化的重要载体,利用七巧板可以拼出许多有趣的图案.现用图1所示的一副七巧板拼成如图2所示的六边形,若图1中七巧板的总面积为16,则图2中六边形的周长为( )
A. B. C. D.
10.如图,将矩形纸片的四个角向内折叠,恰好拼成一个无缝嫩、无重叠的四边形,若,则下列说法正确的是( )
A. B.
C. D.
11.如图,在矩形纸片中,,,点是上一点,点在上,将矩形纸片沿直线折叠,点落在点处.点恰好落在边上的点处,交于点,若,则四边形的面积等于( )
A. B. C. D.
12.如图,在正方形外侧作直线,点C关于直线的对称点为M,连接,.其中交直线于点N.若,则当时,正方形的边长为( )
A. B.5 C. D.
二、填空题
13.若顺次连接一个四边形各边中点所得的图形为矩形,则这个四边形需要满足的条件为______.
14.如图,在平行四边形中,的平分线交边于,平形四边形的周长是,,则=______.
15.如图,在中,,,,为边上一动点,于,于,连接,则的最小值为______.
16.如图,菱形ABCD和菱形EFGH的面积分别为和,CD落在EF上,,若的面积为,则的面积是____.
17.如图,平行四边形中,,,点在边上以每秒的速度从点向点运动,点在边上,以每秒的速度从点出发,在间往返运动,两个点同时出发,当点到达点时停止(同时点也停止).在运动以后,当______时以、、、四点组成的四边形为平行四边形.
三、解答题
18.已知点、分别是平行四边形的边、的中点.
(1)求证:四边形是平行四边形;
(2)若,,求平行四边形的周长.
19.如图,点为正方形对角线上一点, 于点, 于点.
(1)求证:.
(2)若正方形的边长为12,求,四边形的周长.
20.如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=4,∠AOB=60°,求矩形ABCD的面积.
21.如图,在正方形中,为射线上的动点,连接,交于.
(1)证明:;
(2)若交于,当时,求之长;
(3)是否存在点,使得为等腰三角形,若存在,请求出之长;若不存在,请说明理由.
22.问题呈现:(1)如图①,在一次数学折纸活动中,有一张矩形纸片ABCD,点E在AD上,点F在BC上,小华同学将这张矩形纸片沿EF翻折得到四边形,交AD于点H,小华认为EFH是等腰三角形,你认为小华的判断正确吗?请说明理由.
问题拓展:(2)如图②,在“问题呈现”的条件下,当点C的对应点落在AD上时,已知DE=a,CD=b,CF=c,写出a、b、c满足的数量关系,并证明你的结论.
问题应用:(3)如图③,在平行四边形ABCD中,AB=3,AD=4.将平行四边形ABCD沿对角线AC翻折得到ACE,AE交BC于点F.若点F为BC的中点,则平行四边形ABCD的面积为 .
参考答案
1.B
解:A、一组对边平行,另一组对边相等的四边形是平行四边形或等腰梯形,
本选项说法是假命题;
B、对角线互相垂直且平分的四边形是菱形,
本选项说法是真命题;
C、一个角为90°且一组邻边相等的平行四边形是正方形,
本选项说法是假命题;
D、对角线互相平分且相等的四边形是矩形,
本选项说法是假命题;
故选:B.
2.C
A.两组对边分别相等可判断四边形是平行四边形;
B.一组对边平行且相等可判断四边形是平行四边形;
C. 一组对边平行,另一组对边相等不能四边形是平行四边形;
D.两组对边分别平行可判断四边形是平行四边形;
故选C.
3.B
解:∵四边形ABCD是平行四边形,且BD=10,AC=6,
∴AO=OC=AC=3,BO=DO=BD=5,AB=CD,
又∵AB⊥AC,即∠BAC=90°,
∴AB==4,
∴CD=AB=4,
∴BC===,
故选B.
4.D
解:由矩形ABCD,得∠B=∠C=90°,CD=AB,AD=BC,AD∥BC.
由△DEC沿线段DE翻折,点C恰好落在线段AE上的点F处,得△DFE≌△DCE,
∴DF=DC,∠DFE=∠C=90°,
∴DF=AB,∠AFD=90°,
∴∠AFD=∠B,
由AD∥BC得∠DAF=∠AEB,
在△ABE与△DFA中,
,
∴△ABE≌△DFA(AAS).
∵BE:CE=4:1,
∴设CE=x,BE=4x,则AD=BC=5x,
由△ABE≌△DFA,得AF=BE=4x,
在Rt△ADF中,由勾股定理可得DF=3x,
又∵DF=CD=AB=6,
∴x=2,
在Rt△DCE中,DE===2.
故选:D.
5.D
解:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥BD,OA=AC,OB=BD=4,
∴∠AOB=90°,
∵E、F分别是AB、BC边上的中点,
∴EF是△ABC的中位线,
∴AC=2EF=6,
∴OA=3,
∴AB==5,
故选:D.
6.D
解:由图得,大正方形的边长为:,
空白部分的面积为:,
故选D.
7.C
解:四边形是正方形,
,
正方形边长为8,
点A的坐标为
故选C.
8.C
解:设AB=a,BC=b,BE=c,BF=x,
∴S平行四边形EFGH=S矩形ABCD-2(S△BEF+S△AEH)
=ab-2[cx+(a-c)(b-x)]
=ab-(cx+ab-ax-bc+cx)
=ab-cx-ab+ax+bc-cx
=(a-2c)x+bc,
∵F为BC上一动点,
∴x是变量,(a-2c)是x的系数,
∵平行四边形EFGH的面积不会随点F的位置改变而改变,为固定值,
∴x的系数为0,bc为固定值,
∴a-2c=0,
∴a=2c,
∴E是AB的中点,
∴AB=2AE,
故选:C.
9.D
∵图1的总面积为16,
∴正方形的边长为4,
∴①、②的直角边长为,斜边长为4,
④的短边长为,长边长为2,
③的直角边长为,长边长为2,
⑤为正方形,边长为,
⑥的斜边长为2,直角边长为,
⑦的直角边长为,
∴.
故选:D.
10.D
解:∵HJ:JK:KF=2:1:2,
∴设HJ=2x,JK=x,KF=2x,
由折叠的性质得:AH=HJ=2x,
DH =HK=3x,AE=EJ= BE,
∴FH=5x,
∴AH:HD=2:3,
故D说法正确;
故选:D.
11.D
解:∵四边形ABCD是矩形,且
∴
∵
∴
设
∴
∵且
∴
∴
∴
∵∠
∴∠,
∴
∵
∴
∴
∴
∵
∴
设
∴
又
∴
解得,
∴
∵,
∴四边形的面积
故选:D
12.D
解:如图所示,连接、、,
∵点C关于直线的对称点为M,
∴CN=MN,CD=DM,
∴∠NCM=∠NMC,∠DCM=∠DMC,
∴,
在正方形中,,
∴,
∴,
∴,
∵,
∴,
∴是直角三角形,
∴,
∴正方形的边长.
故选:D.
13.对角线互相垂直
解:若一个四边形对角线互相垂直,则顺次连接这个四边形各边中点所得的图形为矩形,
理由如下:∵E,F,G,H分别是AB,BC,CD,DA的中点,
∴EH∥BD,FG∥BD,
∴EH∥FG,
同理,EF∥HG,
∴四边形EFGH是平行四边形,
∵AC⊥BD,
∴EH⊥EF,
∴四边形EFGH是矩形.
故答案为:对角线互相垂直.
14.3
解:四边形是平行四边形,
,,,
,
平行四边形的周长是16,
,
是的平分线,
,
,
,
,
,
,
故答案为:3.
15.
解:,,,
,
为直角三角形,,
于,于,
,
四边形为矩形,
连接,如图,,当的值最小时,的值最小,
当时,的值最小,
根据面积公式,,
,
的最小值为.
故答案为:.
16.8.5
解:连接FH,在菱形和菱形中,,
,
,
,
和同底等高,
菱形的面积为,,
,
,
故答案为:8.5.
17.4.8s或8s或9.6s
解:设经过t秒,以点P、D、Q、B为顶点组成平行四边形,
∵以点P、D、Q、B为顶点组成平行四边形,
∴DP=BQ,
分为以下情况:①点Q的运动路线是C-B,方程为12-4t=12-t,
此时方程t=0,此时不符合题意;
②点Q的运动路线是C-B-C,方程为4t-12=12-t,
解得:t=4.8;
③点Q的运动路线是C-B-C-B,方程为12-(4t-24)=12-t,
解得:t=8;
④点Q的运动路线是C-B-C-B-C,方程为4t-36=12-t,
解得:t=9.6;
综上所述,t=4.8s或8s或9.6s时,以P、D、Q、B四点组成的四边形为平行四边形,
故答案为:4.8s或8s或9.6s.
18.
解:(1)证明:四边形是平行四边形,
,,
点、分别是的边、的中点,
,,
,,
四边形是平行四边形;
(2),,是的中点.
,
四边形是菱形,
的周长.
19.
(1)证明:连接PC,
∵四边形ABCD是正方形,
∴AB=CB,∠ABD=∠CBD=45°,∠BCD=90°,
在△ABP与△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PE⊥CD,PF⊥BC,
∴∠PFC=90°,∠PEC=90°.
又∵∠BCD=90°,
∴四边形PFCE是矩形,
∴EF=PC,
∴PA=EF;
(2)由(1)知四边形PFCE是矩形,
∴PE=CF,PF=CE,
又∵∠CBD=45°,∠PEB=90°,
∴BE=PE,
又∵BC=12,
∴矩形PFCE的周长为2(PE+EC)=2(BE+EC)=2BC=24.
20.(
(1)证明:∵四边形ABCD是矩形,
∴OA=OC,OB=OD,AC=BD,∠ABC=90°,
∵BE=DF,
∴OE=OF,
在△AOE和△COF中,
,
∴△AOE≌△COF(SAS),
∴AE=CF;
(2)解:∵OA=OC,OB=OD,AC=BD,
∴OA=OB,
∵∠AOB=∠COD=60°,
∴△AOB是等边三角形,
∴OA=AB=4,
∴AC=2OA=8,
在Rt△ABC中,,
∴矩形ABCD的面积=AB?BC=4×4=16.
21.
解:(1)证明:四边形是正方形,
,,
在和中,
,
;
(2)如图1,
,
,
,
,
,
,
,
,
,
,,
,
,
;
(3)当时,
,
,即,
点与点重合,
;
当时,
,
,
是的一个锐角,
,
不存在;
当时,
,
,
如图2,在上截取,连接,
,,
,
,
,
,
,
综上所述:或.
22.
解:(1)小华的判断是正确的.
在矩形ABCD中, AD∥BC,∴∠HEF=∠EFC.
由折叠,得∠HFE=∠EFC,
∴∠HFE=∠HEF
∴HE=HF
∴△EFH是等腰三角形
(2).
在矩形ABCD中,∠D=90°,
由折叠,得,,,,
由问题呈现,得.
在Rt△中,,
∴.
(3)∵四边形ABCD为平行四边形,AB=3,AD=4,
∴CD=3,BC=4,∠B=∠D,
由折叠性质可知,EC=CD,AE=AD=4,∠E=∠D,
∴EC=AB,∠B=∠E,
∵点F为BC的中点,
∴BF=CF,
∵∠AFB=∠EFC,
∴△AFB≌△EFC(AAS),
∴AF=FE=AE=×4=2.
∴BF=AF=2,
如图,过点F作FH⊥AB于H,
则AH=BH=AB=×3=,
在Rt△BHF中,HF=,
∴S△ABF=AB?HF=×3×=,
∴S?ABCD=4S△ABF=4×=.
故答案为:
