1.1.2 余弦定理 人教A版高中数学必修5(共25张PPT)
文档属性
| 名称 | 1.1.2 余弦定理 人教A版高中数学必修5(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 10:10:51 | ||
图片预览




文档简介
(共25张PPT)
人教A版
数学
必修五第一章第一节
1.1.2
余弦定理
复习回顾
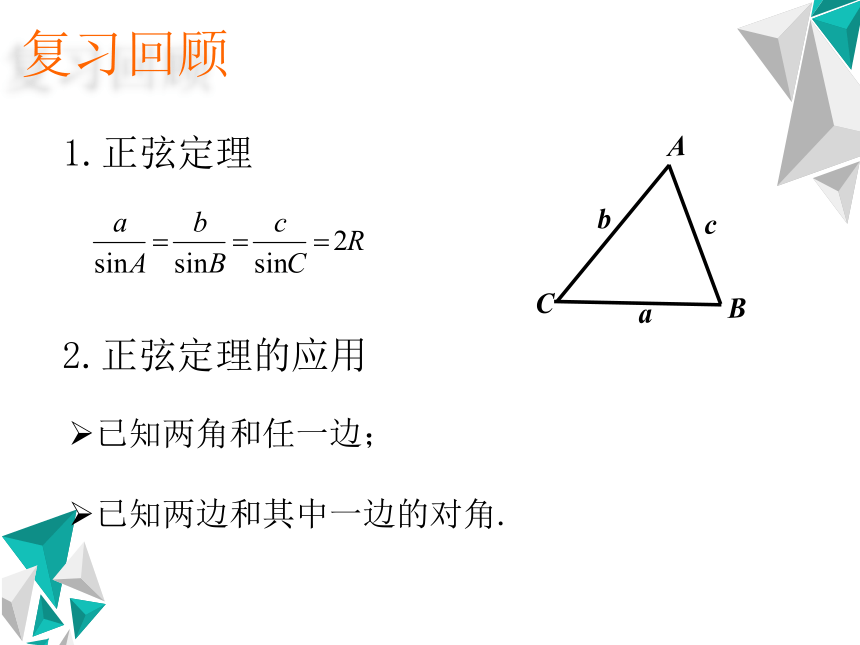
1.正弦定理
A
B
C
c
a
b
已知两角和任一边;
已知两边和其中一边的对角.
2.正弦定理的应用
创
设
情
景
B
A
C
20m
50m
?
B
A
C
20m
50m
?
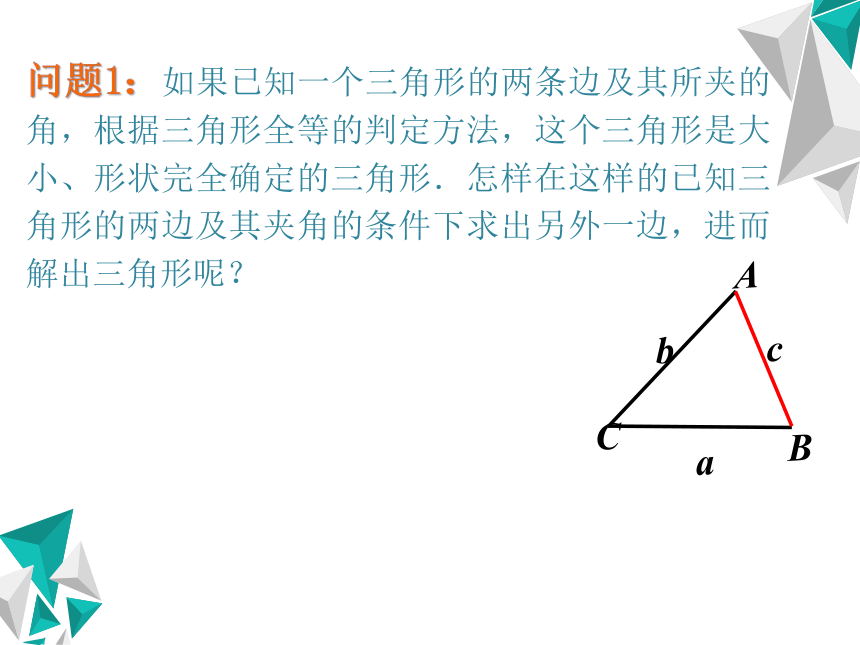
问题1:如果已知一个三角形的两条边及其所夹的角,根据三角形全等的判定方法,这个三角形是大小、形状完全确定的三角形.怎样在这样的已知三角形的两边及其夹角的条件下求出另外一边,进而解出三角形呢?
C
B
A
c
a
b
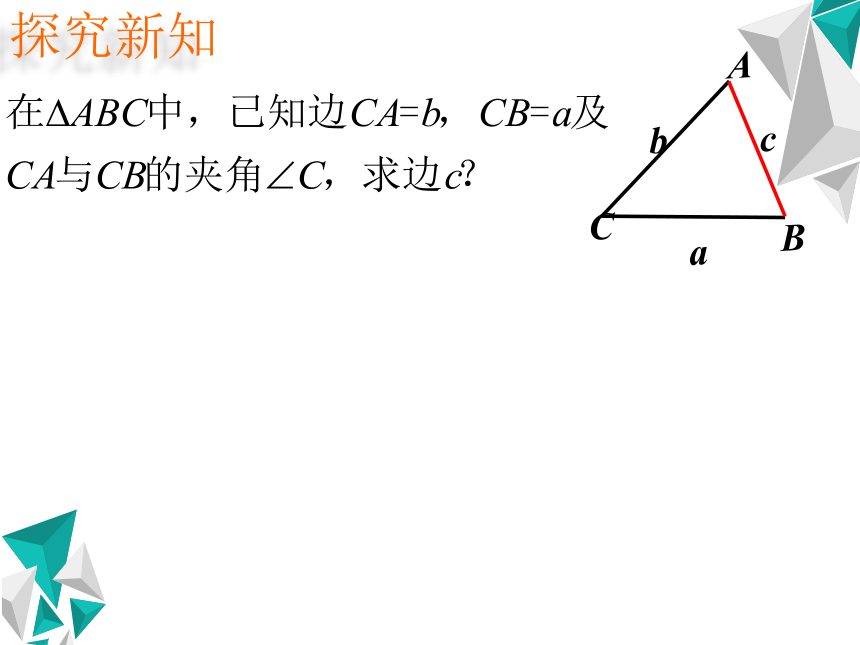
探究新知
C
B
A
c
a
b
C
B
A
c
a
b
﹚
由向量减法的三角形法则得
设
探究
向量法
思考:你能用坐标法证明余弦定理?还有其他方法吗?
B
C
A
﹙a,o﹚
b
(bcosC,bsinC)
a
c
AB2=(bcosC-a)2+(bsinC-0)2
A
B
C
a
b
c
D
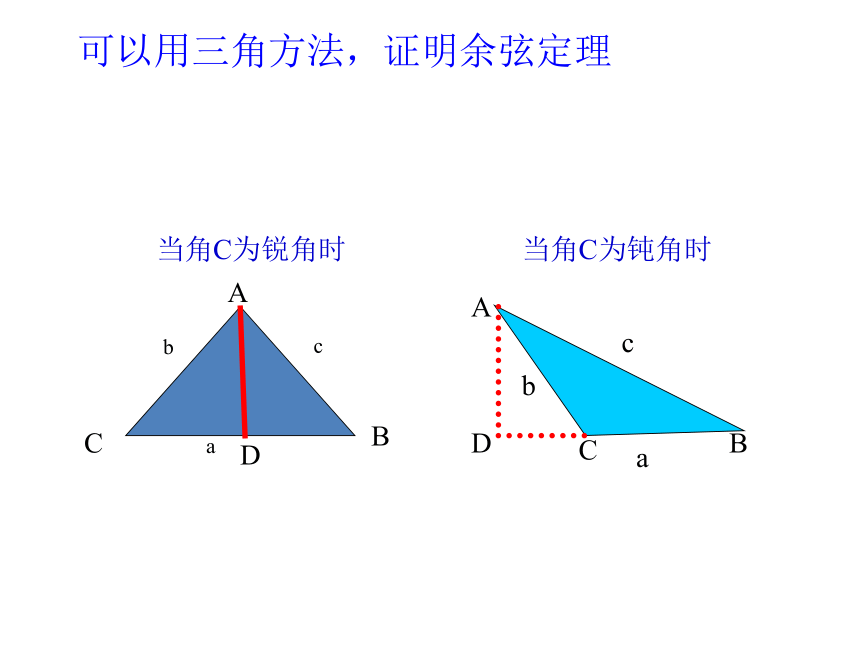
当角C为锐角时
b
A
a
c
C
B
D
当角C为钝角时
可以用三角方法,证明余弦定理
C
B
A
c
a
b
﹚
由向量减法的三角形法则得
设
探究
C
B
A
c
a
b
﹚
余弦定理
由向量减法的三角形法则得
设
探究
定理辨析
余弦定理:三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。
公式表示:
余弦定理及其推论
问题2:余弦定理与以前的关于三角形的什么定理在形式上非常相近?
余弦定理可以看作是勾股定理的推广,勾股定理是余弦定理的特例
余弦定理及其推论
问题3:我们得到的余弦定理是关于三角形三边和一个角的关系式.
把这个关系式作某些变形,是否可以解决其他类型的解三角形问题?
从余弦定理,可以得到它的推论
余弦定理的推论
B
ac
c
a
b
cos
2
2
2
2
-
+
=
思考
如果已知三角形的三边,如何确定三个角?
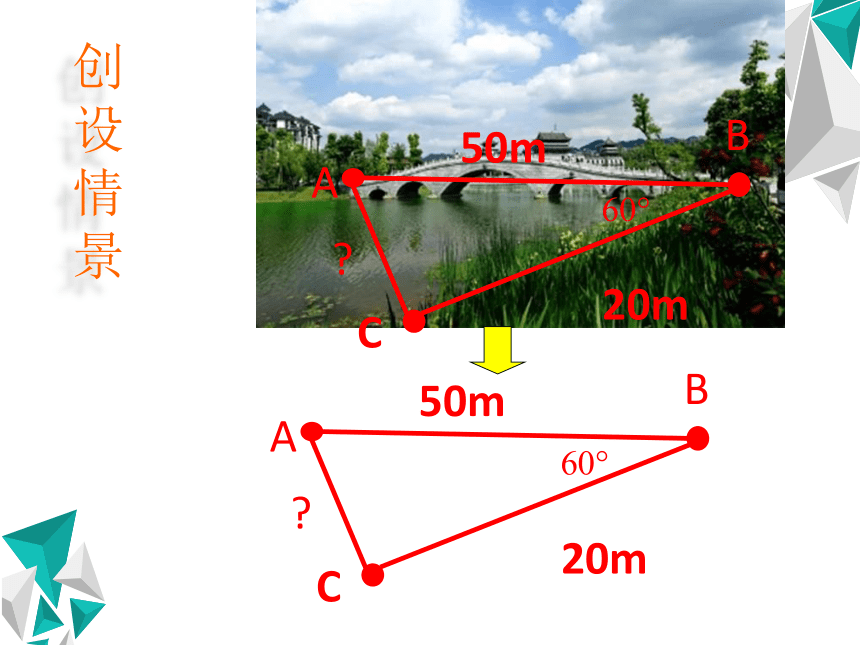
在△ABC中,已知AB=50m,BC=20m,
∠B=60o,求
AC
解决“秀湖问题”例1
解:由余弦定理得
答:A与C的距离为
m.
B
A
C
20m
50m
?
新知应用
课堂检测
课堂小结
1.余弦定理的证明方法:
几何法;
向量法;
坐标法.
2.余弦定理的作用:
已知两边及其夹角求第三边;
已知三边求内角.
问题5:证明余弦定理我们用了哪些方法?应用余弦定理可以解决哪些类型的解三角形问题?
思想方法:转化与化归思想
量化思想
方程思想
数形结合思想
作业布置
余弦定理是在欧几里得的《几何原本》第二卷中间接提出来的,余弦定理的确立和运用是随航海学和地理学的发展,人们对球面三角进行研究而得出的“副产品”。
在十五世纪前叶,阿拉伯数学家阿尔·卡西给出了平面三角的余弦定理的下述形式:
韦达在1593年给出了平面三角的余弦定理的下述形式:
余弦定理的证明方法:几何法、坐标法、向量法等。
参考文献:陈克胜.“余弦定理和正弦定理”的数学思想史略[J].数学通讯.2004(21)
知识拓展——余弦定理的数学发展史略
谢谢大家!
证明:在三角形ABC中,已知AB=c,AC=b和A
作CD⊥AB,则CD=bsinA,BD=c-bcosA
A
B
C
c
b
a
同理有:
思考5:若△ABC为钝角三角形,该如何证明?
是否还有其他证明方法?(课后自己完成)
D
几何法
A
B
C
c
b
a
D
新知应用
人教A版
数学
必修五第一章第一节
1.1.2
余弦定理
复习回顾
1.正弦定理
A
B
C
c
a
b
已知两角和任一边;
已知两边和其中一边的对角.
2.正弦定理的应用
创
设
情
景
B
A
C
20m
50m
?
B
A
C
20m
50m
?
问题1:如果已知一个三角形的两条边及其所夹的角,根据三角形全等的判定方法,这个三角形是大小、形状完全确定的三角形.怎样在这样的已知三角形的两边及其夹角的条件下求出另外一边,进而解出三角形呢?
C
B
A
c
a
b
探究新知
C
B
A
c
a
b
C
B
A
c
a
b
﹚
由向量减法的三角形法则得
设
探究
向量法
思考:你能用坐标法证明余弦定理?还有其他方法吗?
B
C
A
﹙a,o﹚
b
(bcosC,bsinC)
a
c
AB2=(bcosC-a)2+(bsinC-0)2
A
B
C
a
b
c
D
当角C为锐角时
b
A
a
c
C
B
D
当角C为钝角时
可以用三角方法,证明余弦定理
C
B
A
c
a
b
﹚
由向量减法的三角形法则得
设
探究
C
B
A
c
a
b
﹚
余弦定理
由向量减法的三角形法则得
设
探究
定理辨析
余弦定理:三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。
公式表示:
余弦定理及其推论
问题2:余弦定理与以前的关于三角形的什么定理在形式上非常相近?
余弦定理可以看作是勾股定理的推广,勾股定理是余弦定理的特例
余弦定理及其推论
问题3:我们得到的余弦定理是关于三角形三边和一个角的关系式.
把这个关系式作某些变形,是否可以解决其他类型的解三角形问题?
从余弦定理,可以得到它的推论
余弦定理的推论
B
ac
c
a
b
cos
2
2
2
2
-
+
=
思考
如果已知三角形的三边,如何确定三个角?
在△ABC中,已知AB=50m,BC=20m,
∠B=60o,求
AC
解决“秀湖问题”例1
解:由余弦定理得
答:A与C的距离为
m.
B
A
C
20m
50m
?
新知应用
课堂检测
课堂小结
1.余弦定理的证明方法:
几何法;
向量法;
坐标法.
2.余弦定理的作用:
已知两边及其夹角求第三边;
已知三边求内角.
问题5:证明余弦定理我们用了哪些方法?应用余弦定理可以解决哪些类型的解三角形问题?
思想方法:转化与化归思想
量化思想
方程思想
数形结合思想
作业布置
余弦定理是在欧几里得的《几何原本》第二卷中间接提出来的,余弦定理的确立和运用是随航海学和地理学的发展,人们对球面三角进行研究而得出的“副产品”。
在十五世纪前叶,阿拉伯数学家阿尔·卡西给出了平面三角的余弦定理的下述形式:
韦达在1593年给出了平面三角的余弦定理的下述形式:
余弦定理的证明方法:几何法、坐标法、向量法等。
参考文献:陈克胜.“余弦定理和正弦定理”的数学思想史略[J].数学通讯.2004(21)
知识拓展——余弦定理的数学发展史略
谢谢大家!
证明:在三角形ABC中,已知AB=c,AC=b和A
作CD⊥AB,则CD=bsinA,BD=c-bcosA
A
B
C
c
b
a
同理有:
思考5:若△ABC为钝角三角形,该如何证明?
是否还有其他证明方法?(课后自己完成)
D
几何法
A
B
C
c
b
a
D
新知应用
