1.4.1 正弦函数、余弦函数的图像 人教A版高中数学必修4(共23张PPT)
文档属性
| 名称 | 1.4.1 正弦函数、余弦函数的图像 人教A版高中数学必修4(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 00:00:00 | ||
图片预览




文档简介
(共23张PPT)
正弦函数、余弦函数的图象
三角函数
三角函数线
正弦函数
余弦函数
正切函数
正切线AT
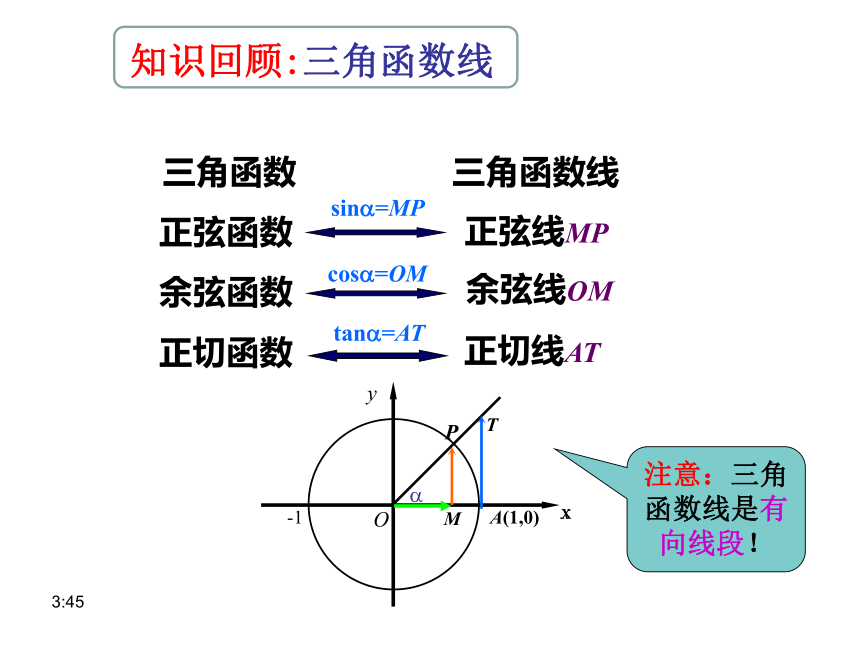
知识回顾:三角函数线
y
x
x
O
-1
?
P
M
A(1,0)
T
sin?=MP
cos?=OM
tan?=AT
注意:三角函数线是有向线段!
正弦线MP
余弦线OM
任意给定一个实数x,有唯一确定的值sinx与之
对应。由这个对应法则所确定的函数
叫
做正弦函数,
叫做余弦函数,二者定义
域都为
。
R
正弦函数、余弦函数的定义
y=sinx
y=cosx
合作探究1:正弦函数图象
描点法
有哪些步骤?
列表、描点、连线
思考1:画函数图象的常用方法:
思考2:用描点法作正弦函数y=sinx在[0,2π]内的图象,可取哪些点?
(1)
列表
(2)
描点
(3)
连线
作图:用描点法画正弦函数的图象
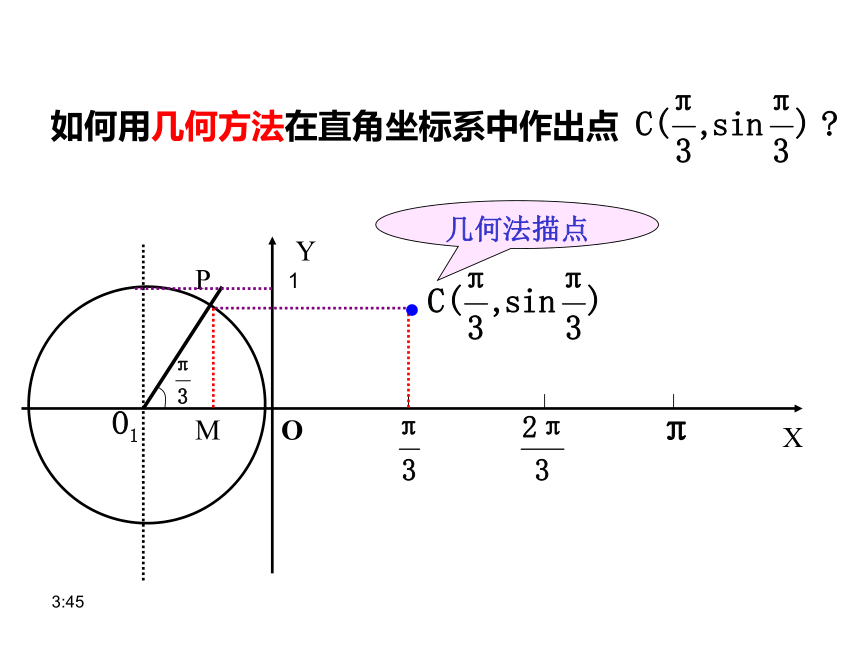
如何用几何方法在直角坐标系中作出点
O
P
M
X
Y
.
几何法描点
1
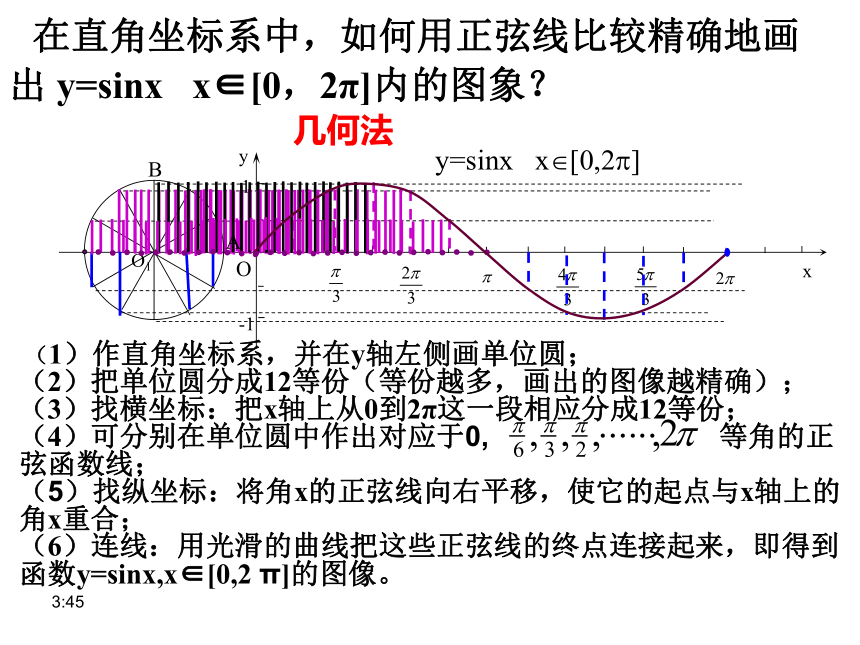
在直角坐标系中,如何用正弦线比较精确地画出
y=sinx
x∈[0,2π]内的图象?
y=sinx
x?[0,2?]
O1
O
y
x
-1
1
A
B
(1)作直角坐标系,并在y轴左侧画单位圆;
(2)把单位圆分成12等份(等份越多,画出的图像越精确);
(3)找横坐标:把x轴上从0到2π这一段相应分成12等份;
(4)可分别在单位圆中作出对应于0,
等角的正弦函数线;
(5)找纵坐标:将角x的正弦线向右平移,使它的起点与x轴上的角x重合;
(6)连线:用光滑的曲线把这些正弦线的终点连接起来,即得到函数y=sinx,x∈[0,2
π]的图像。
几何法
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
正弦曲线
y=sinx
x?[0,2?]
y=sinx
x?R
终边相同角的三角函数值相等
即:
sin(x+2k?)=sinx,
k?Z
利用图象平移
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
余弦函数的图象
正弦函数的图象
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
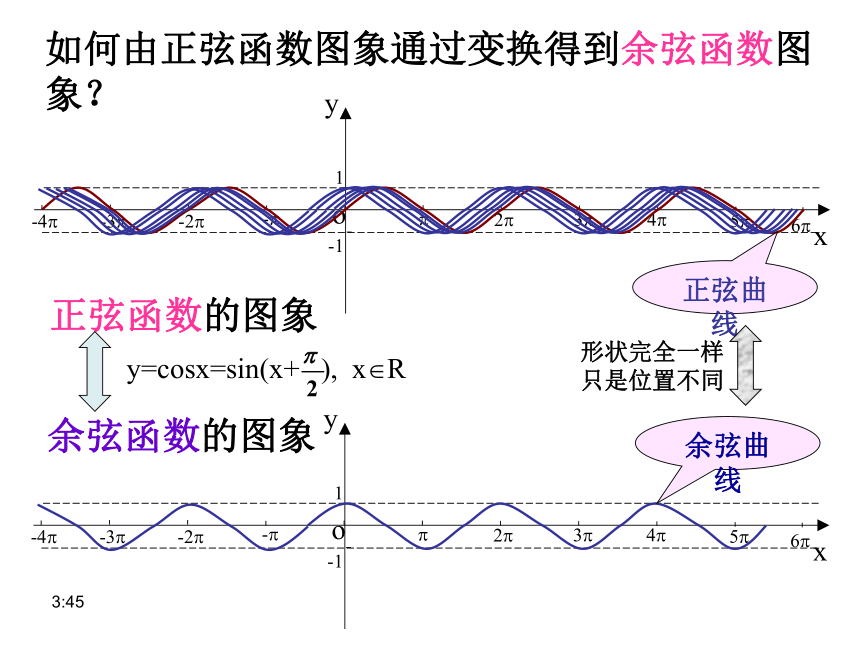
y=cosx=sin(x+
),
x?R
余弦曲线
正弦曲线
形状完全一样只是位置不同
如何由正弦函数图象通过变换得到余弦函数图象?
正弦函数图象的关键点
y
x
o
1
-1
(0,0)
(
,1)
(
?
,0)
(
,-1)
(
2?
,0)
五个关键点
—
(0,0)
(
,1)
(
?
,0)
(
,1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,-1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,-1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,-1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,-1)
(
2?
,0)
图象的最高点
与x轴的交点
图象的最低点
方法总结:
在精确度要求不高时,先作出函数y=sinx和y=
cosx的五个关键点,再用光滑的曲线将它们顺次连结起来,就得到函数的简图。这种作图法叫做“五点(画图)法”。
方法总结:在精确度要求不高时,先作出函数y=sinx的五个关键点,再用光滑的曲线将它们连结起来,就得到函数的简图。这种作图法叫做“五点(画图)法”。
y
x
o
1
-1
y=cosx,x?[0,
2?]
找出余弦函数y=
cosx,x?[0,
2?]图象的五个关键点:
(0,1)
(
,0)
(
?
,-1)
(
,
0)
(
2?
,1)
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
例1
(1)画出函数y=1+sinx,x?[0,
2?]的简图:
x
sinx
1+sinx
0
?
2
?
0
1
0
-1
0
1
2
1
0
1
o
1
y
x
-1
2
步骤:
1.列表
2.描点
3.连线
y=sinx,x?[0,
2?]
y=1+sinx,x?[0,
2?]
(2)
画出函数y=
-
cosx,x?[0,
2?]的简图:
x
cosx
-
cosx
0
?
2
?
1
0
-1
0
1
-1
0
1
0
-1
y
x
o
1
-1
y=
-
cosx,x?[0,
2?]
y=cosx,x?[0,
2?]
例1(3)利用正弦函数图象变换作出下列函数的简图:y=|sinx|,x∈[0,4π].
首先用五点法作出函数y=sinx,x∈[0,4π]的图象,再将x轴下方的部分对称翻折到x轴的上方.如图所示.
〖例2
〗根据余弦函数图象写出使不等式cosx>
x∈[0,2π]成立的x的取值集合
x
y
O
2π
π
1
-1
例3.结合图象,判断方程
的实数
解的个数.
6
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
6
(6,1)
1.用五点作图法画出y=sin2x,x∈[0,π]的简图.
2.方程
的根的个数为( )
课堂练习
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
10
7
(10,1)
描点法
几何作图法(三角函数线)
五点作图法
1.作图方法
图象变换法
平移变换、对称变换、
翻折变换
y
x
o
1
-1
y=sinx,x?[0,
2?]
y=cosx,x?[0,
2?]
2.
正弦曲线、余弦曲线以及两者之间的区别和联系.
课后练习
,
3.画出函数y=sin|x|,x∈R的图像
1.用五点作图法画出下列函数的简图.
?
2.
3.把y=sin
x图像在y轴右侧的部分保留,去掉y轴左侧的图像,再把y轴右
侧的图像沿y轴翻折到y轴左侧,就可得y=sin
|x|的图像.
1.
若方程m=sin
x+2|sin
x|,x∈[0,2π]有且只有两个不相等的实数根,求实数m的取值范围.
[巧思] 方程m=sin
x+2|sin
x|,x∈[0,2π]的解的个数即为直线y=m与y=sin
x+2|sin
x|,x∈[0,2π]的图像的交点的个数,因此可画出函数y=sin
x+2|sin
x|,x∈[0,2π]的图像,利用数形结合的思想解决.
可知12.方程cos
x=lg
x的实根的个数是
( )
A.1
B.2
C.3
D.无数
答案:C
解析:作出函数y=cos
x和y=lg
x的图像.两曲线有3个交点,故方程有3个实根.
正弦函数、余弦函数的图象
三角函数
三角函数线
正弦函数
余弦函数
正切函数
正切线AT
知识回顾:三角函数线
y
x
x
O
-1
?
P
M
A(1,0)
T
sin?=MP
cos?=OM
tan?=AT
注意:三角函数线是有向线段!
正弦线MP
余弦线OM
任意给定一个实数x,有唯一确定的值sinx与之
对应。由这个对应法则所确定的函数
叫
做正弦函数,
叫做余弦函数,二者定义
域都为
。
R
正弦函数、余弦函数的定义
y=sinx
y=cosx
合作探究1:正弦函数图象
描点法
有哪些步骤?
列表、描点、连线
思考1:画函数图象的常用方法:
思考2:用描点法作正弦函数y=sinx在[0,2π]内的图象,可取哪些点?
(1)
列表
(2)
描点
(3)
连线
作图:用描点法画正弦函数的图象
如何用几何方法在直角坐标系中作出点
O
P
M
X
Y
.
几何法描点
1
在直角坐标系中,如何用正弦线比较精确地画出
y=sinx
x∈[0,2π]内的图象?
y=sinx
x?[0,2?]
O1
O
y
x
-1
1
A
B
(1)作直角坐标系,并在y轴左侧画单位圆;
(2)把单位圆分成12等份(等份越多,画出的图像越精确);
(3)找横坐标:把x轴上从0到2π这一段相应分成12等份;
(4)可分别在单位圆中作出对应于0,
等角的正弦函数线;
(5)找纵坐标:将角x的正弦线向右平移,使它的起点与x轴上的角x重合;
(6)连线:用光滑的曲线把这些正弦线的终点连接起来,即得到函数y=sinx,x∈[0,2
π]的图像。
几何法
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
正弦曲线
y=sinx
x?[0,2?]
y=sinx
x?R
终边相同角的三角函数值相等
即:
sin(x+2k?)=sinx,
k?Z
利用图象平移
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
余弦函数的图象
正弦函数的图象
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y=cosx=sin(x+
),
x?R
余弦曲线
正弦曲线
形状完全一样只是位置不同
如何由正弦函数图象通过变换得到余弦函数图象?
正弦函数图象的关键点
y
x
o
1
-1
(0,0)
(
,1)
(
?
,0)
(
,-1)
(
2?
,0)
五个关键点
—
(0,0)
(
,1)
(
?
,0)
(
,1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,-1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,-1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,-1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,-1)
(
2?
,0)
图象的最高点
与x轴的交点
图象的最低点
方法总结:
在精确度要求不高时,先作出函数y=sinx和y=
cosx的五个关键点,再用光滑的曲线将它们顺次连结起来,就得到函数的简图。这种作图法叫做“五点(画图)法”。
方法总结:在精确度要求不高时,先作出函数y=sinx的五个关键点,再用光滑的曲线将它们连结起来,就得到函数的简图。这种作图法叫做“五点(画图)法”。
y
x
o
1
-1
y=cosx,x?[0,
2?]
找出余弦函数y=
cosx,x?[0,
2?]图象的五个关键点:
(0,1)
(
,0)
(
?
,-1)
(
,
0)
(
2?
,1)
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
例1
(1)画出函数y=1+sinx,x?[0,
2?]的简图:
x
sinx
1+sinx
0
?
2
?
0
1
0
-1
0
1
2
1
0
1
o
1
y
x
-1
2
步骤:
1.列表
2.描点
3.连线
y=sinx,x?[0,
2?]
y=1+sinx,x?[0,
2?]
(2)
画出函数y=
-
cosx,x?[0,
2?]的简图:
x
cosx
-
cosx
0
?
2
?
1
0
-1
0
1
-1
0
1
0
-1
y
x
o
1
-1
y=
-
cosx,x?[0,
2?]
y=cosx,x?[0,
2?]
例1(3)利用正弦函数图象变换作出下列函数的简图:y=|sinx|,x∈[0,4π].
首先用五点法作出函数y=sinx,x∈[0,4π]的图象,再将x轴下方的部分对称翻折到x轴的上方.如图所示.
〖例2
〗根据余弦函数图象写出使不等式cosx>
x∈[0,2π]成立的x的取值集合
x
y
O
2π
π
1
-1
例3.结合图象,判断方程
的实数
解的个数.
6
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
6
(6,1)
1.用五点作图法画出y=sin2x,x∈[0,π]的简图.
2.方程
的根的个数为( )
课堂练习
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
10
7
(10,1)
描点法
几何作图法(三角函数线)
五点作图法
1.作图方法
图象变换法
平移变换、对称变换、
翻折变换
y
x
o
1
-1
y=sinx,x?[0,
2?]
y=cosx,x?[0,
2?]
2.
正弦曲线、余弦曲线以及两者之间的区别和联系.
课后练习
,
3.画出函数y=sin|x|,x∈R的图像
1.用五点作图法画出下列函数的简图.
?
2.
3.把y=sin
x图像在y轴右侧的部分保留,去掉y轴左侧的图像,再把y轴右
侧的图像沿y轴翻折到y轴左侧,就可得y=sin
|x|的图像.
1.
若方程m=sin
x+2|sin
x|,x∈[0,2π]有且只有两个不相等的实数根,求实数m的取值范围.
[巧思] 方程m=sin
x+2|sin
x|,x∈[0,2π]的解的个数即为直线y=m与y=sin
x+2|sin
x|,x∈[0,2π]的图像的交点的个数,因此可画出函数y=sin
x+2|sin
x|,x∈[0,2π]的图像,利用数形结合的思想解决.
可知1
x=lg
x的实根的个数是
( )
A.1
B.2
C.3
D.无数
答案:C
解析:作出函数y=cos
x和y=lg
x的图像.两曲线有3个交点,故方程有3个实根.
