2020-2021 高中数学人教版必修四第二章平面向量小结与复习(共20张PPT)
文档属性
| 名称 | 2020-2021 高中数学人教版必修四第二章平面向量小结与复习(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
第二章
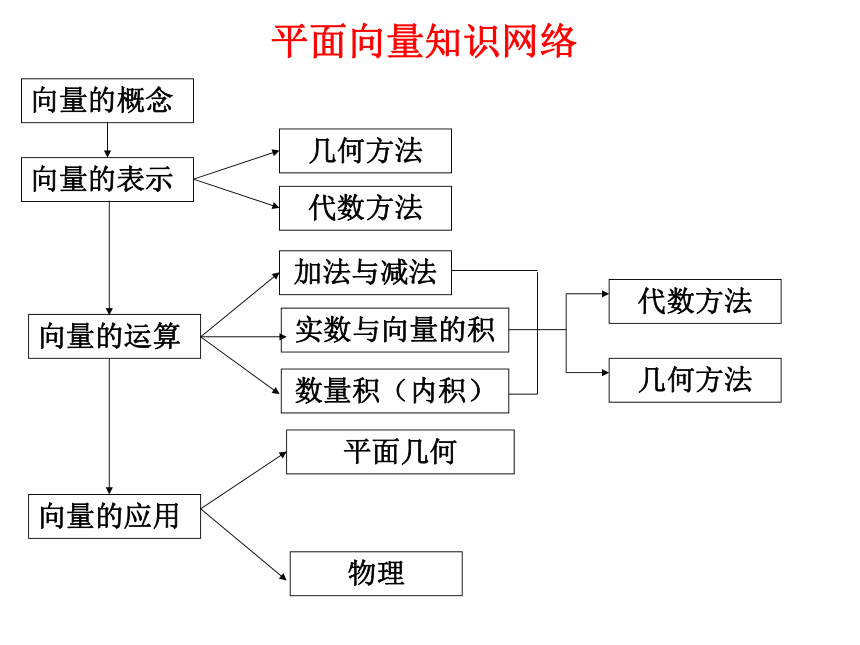
平面向量小结与复面向量知识网络
向量的概念
向量的表示
向量的运算
向量的应用
几何方法
代数方法
加法与减法
实数与向量的积
数量积(内积)
几何方法
代数方法
平面几何
物理
知识要点:
1.向量在几何中的应用
平面几何图形中的很多性质,如长度、夹角、平行、垂直等都可以用平面向量的数量积与共线向量来解决.
2.向量在三角中的应用
(1)以向量为载体研究三角函数中的最值、单调性、周期性等问题;
(2)通过向量的线性运算及数量积、共线来解决三角形中形状的判断、边角的大小关系.
3.向量在物理学中的应用
由于力、速度是向量,它们的分解与合成与向量的加减法类似,可以用向量方法来解决,力作的功就是向量中数量积的一种体现.
例1.
(1)有四个式子:⑴ ⑵ ⑶
⑷ 其中正确的个数为(
)
A、4个 B、3个 C、2个 D、1个
(2)已知 、 都是单位向量,下列结论正确的是(
)
A、 B、 C、
∥ D、
(3)有下列四个关系式:⑴ ⑵ ⑶ ⑷ ,其中正确的个数是( )
A、1 B、2 C、3 D、4
D
B
A
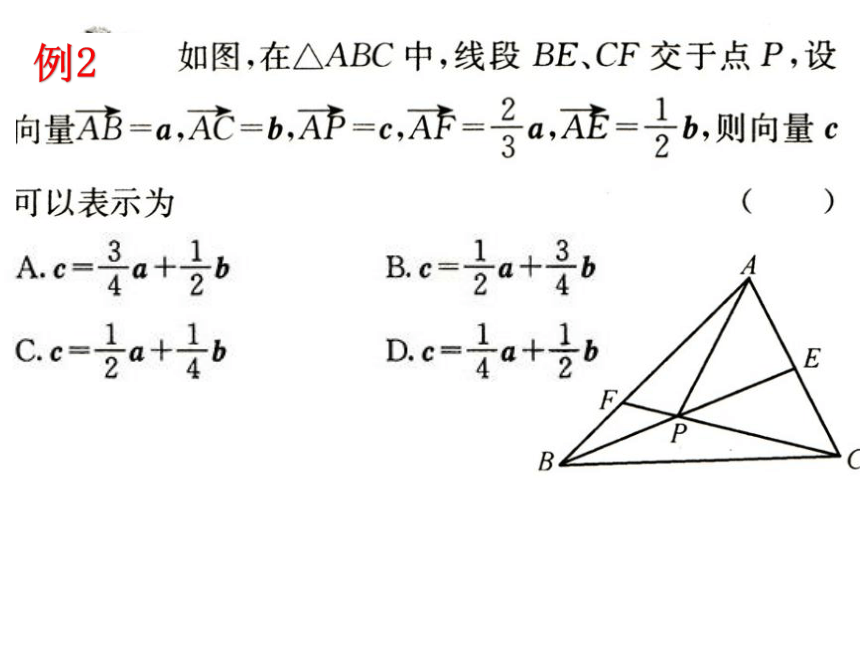
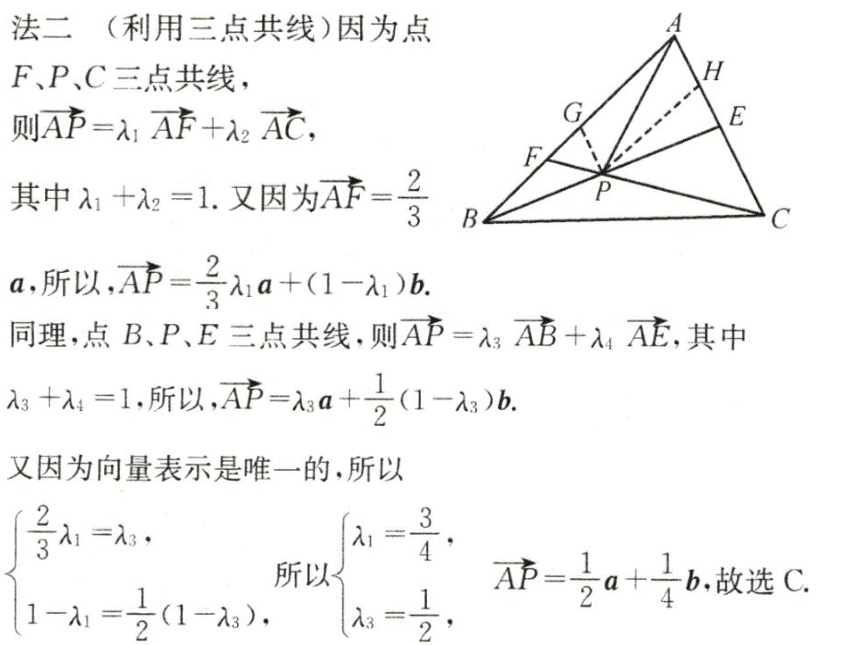
例2
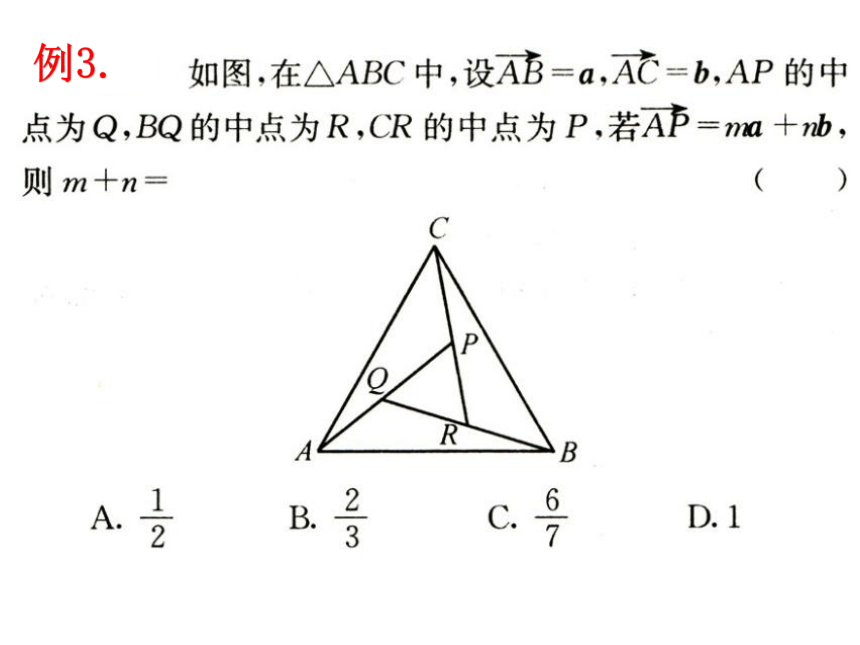
例3.
例4.
问:λ为何值时,θ为直角?锐角?钝角?
它们的夹角为θ,
解:
且
且
且
且
已知
解:
(1)由题意,
则
,
解:
(2)
则
,
例6.
解:
∴
∴
B
例6.
解:
解:
例7.
例7.
例8.
课后作业
2.《向量》错题整理
1.复习参考题二(电子作业)
第二章
平面向量小结与复面向量知识网络
向量的概念
向量的表示
向量的运算
向量的应用
几何方法
代数方法
加法与减法
实数与向量的积
数量积(内积)
几何方法
代数方法
平面几何
物理
知识要点:
1.向量在几何中的应用
平面几何图形中的很多性质,如长度、夹角、平行、垂直等都可以用平面向量的数量积与共线向量来解决.
2.向量在三角中的应用
(1)以向量为载体研究三角函数中的最值、单调性、周期性等问题;
(2)通过向量的线性运算及数量积、共线来解决三角形中形状的判断、边角的大小关系.
3.向量在物理学中的应用
由于力、速度是向量,它们的分解与合成与向量的加减法类似,可以用向量方法来解决,力作的功就是向量中数量积的一种体现.
例1.
(1)有四个式子:⑴ ⑵ ⑶
⑷ 其中正确的个数为(
)
A、4个 B、3个 C、2个 D、1个
(2)已知 、 都是单位向量,下列结论正确的是(
)
A、 B、 C、
∥ D、
(3)有下列四个关系式:⑴ ⑵ ⑶ ⑷ ,其中正确的个数是( )
A、1 B、2 C、3 D、4
D
B
A
例2
例3.
例4.
问:λ为何值时,θ为直角?锐角?钝角?
它们的夹角为θ,
解:
且
且
且
且
已知
解:
(1)由题意,
则
,
解:
(2)
则
,
例6.
解:
∴
∴
B
例6.
解:
解:
例7.
例7.
例8.
课后作业
2.《向量》错题整理
1.复习参考题二(电子作业)
