2020-2021 高中数学人教版必修四解决向量问题常用方法总结(共22张PPT)
文档属性
| 名称 | 2020-2021 高中数学人教版必修四解决向量问题常用方法总结(共22张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
解决向量问题常用方法总结
O
A
B
C
B
A
O
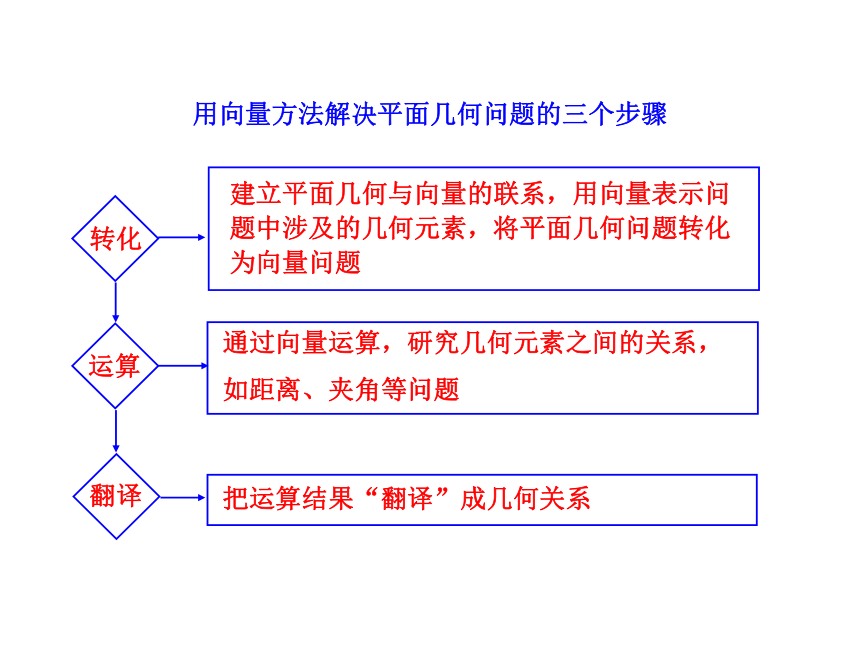
1.平面向量知识框架图
实际背景
平面向量
加、减法
数乘
定义
性质
运算律
定义
性质
运算律
定义
性质
运算律
共线向量
平面向量基本定理及坐标表示
向量在几何中的应用
向量在物理中的应用
向量的基本概念
向量的线性运算
向量的数量积
向量的应用举例
用向量方法解决平面几何问题的三个步骤
建立平面几何与向量的联系,用向量表示问
题中涉及的几何元素,将平面几何问题转化
为向量问题
通过向量运算,研究几何元素之间的关系,如距离、夹角等问题
把运算结果“翻译”成几何关系
转化
运算
翻译
基本思想
1.数形结合
2.转化与化归
常用方法
1.作图:充分利用向量的几何特性,掌握线性运算(三角形法则、平行四边形法则)的几何特征,利用几何作图解题;
2.基底法:“恰当选择基底”.选择一组基底,再用该基底表示向量,其实质就是利用平行四边形法则或三角形法则进行向量的加减运算和数乘运算;
3.坐标法:对于题目中有特殊角的向量问题,利用坐标建系,达到转化问题,简单求解的目的
1.A
2.B
解类题
·
融会贯通
练习:
方法总结
基本思想
1.数形结合
2.转化与化归
常用方法
1.作图:充分利用向量的几何特性,掌握线性运算(三角形法则、平行四边形法则)的几何特征,利用几何作图解题;
2.基底法:“恰当选择基底”.选择一组基底,再用该基底表示向量,其实质就是利用平行四边形法则或三角形法则进行向量的加减运算和数乘运算;
3.坐标法:对于题目中有特殊角的向量问题,利用坐标建系,达到转化问题,简单求解的目的
课后思考:
Thank
you
for
watching
谢谢指导!
解决向量问题常用方法总结
O
A
B
C
B
A
O
1.平面向量知识框架图
实际背景
平面向量
加、减法
数乘
定义
性质
运算律
定义
性质
运算律
定义
性质
运算律
共线向量
平面向量基本定理及坐标表示
向量在几何中的应用
向量在物理中的应用
向量的基本概念
向量的线性运算
向量的数量积
向量的应用举例
用向量方法解决平面几何问题的三个步骤
建立平面几何与向量的联系,用向量表示问
题中涉及的几何元素,将平面几何问题转化
为向量问题
通过向量运算,研究几何元素之间的关系,如距离、夹角等问题
把运算结果“翻译”成几何关系
转化
运算
翻译
基本思想
1.数形结合
2.转化与化归
常用方法
1.作图:充分利用向量的几何特性,掌握线性运算(三角形法则、平行四边形法则)的几何特征,利用几何作图解题;
2.基底法:“恰当选择基底”.选择一组基底,再用该基底表示向量,其实质就是利用平行四边形法则或三角形法则进行向量的加减运算和数乘运算;
3.坐标法:对于题目中有特殊角的向量问题,利用坐标建系,达到转化问题,简单求解的目的
1.A
2.B
解类题
·
融会贯通
练习:
方法总结
基本思想
1.数形结合
2.转化与化归
常用方法
1.作图:充分利用向量的几何特性,掌握线性运算(三角形法则、平行四边形法则)的几何特征,利用几何作图解题;
2.基底法:“恰当选择基底”.选择一组基底,再用该基底表示向量,其实质就是利用平行四边形法则或三角形法则进行向量的加减运算和数乘运算;
3.坐标法:对于题目中有特殊角的向量问题,利用坐标建系,达到转化问题,简单求解的目的
课后思考:
Thank
you
for
watching
谢谢指导!
