河北廊坊固安县彭村乡中学2020-2021学年七年级下学期阶段性(5月)评估(A)数学试卷(word解析版)
文档属性
| 名称 | 河北廊坊固安县彭村乡中学2020-2021学年七年级下学期阶段性(5月)评估(A)数学试卷(word解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 913.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-31 00:00:00 | ||
图片预览


文档简介
20210-2021学年第二学期彭村中学七年级阶段性评估数学A卷
学校:___________姓名:___________班级:___________考号:___________
一、单选题(1-10题每小题3分,11-26题每小题2分,共42分。)
1.下列图形中,和是对顶角的是(
)
A.
B.
C.
D.
2.下列各现象中:
①电梯的升降;
②照镜子;
③钟表分针的运动;
④行驶中汽车车轮的运动.
其中是平移现象的有(
)
A.1个
B.2个
C.3个
D.4个
3.在同一平面内,两条直线的位置关系有(
)
A.平行和相交
B.平行和垂直
C.平行、垂直和相交
D.垂直和相交
4.如图所示,直线相交于点,于点,平分,,则下列结论不正确的是(
)
A.
B.
C.与互为补角
D.的余角等于
5.将一副三角板按如图5-6-2所示的方式放置,下列结论中不正确的是(
)
A.若,则有
B.
C.若,则有
D.如果,必有
6.如图,直线则等于(
)
A.150°
B.180°
C.210°
D.240°
7.如图所示,在平面直角坐标系中,点的坐标分别为,将沿一确定方向平移得到,点B的对应点的坐标是则点的坐标分别是(
)
A.
B.
C.
D.
8.如图所示,若,则
①;
②;
③.
其中正确的个数为(
)
A.0
B.1
C.2
D.3
9.如图,在中,,把沿着直线的方向平移2.5cm后得到,连接,有以下结论:
①;
②;
③;
④.
其中正确的结论有(
)
A.1个
B.2个
C.3个
D.4个
10.如图,已知直线,直角三角板的直角顶点在直线a上,若,则等于(
)
A.30°
B.40°
C.50°
D.60°
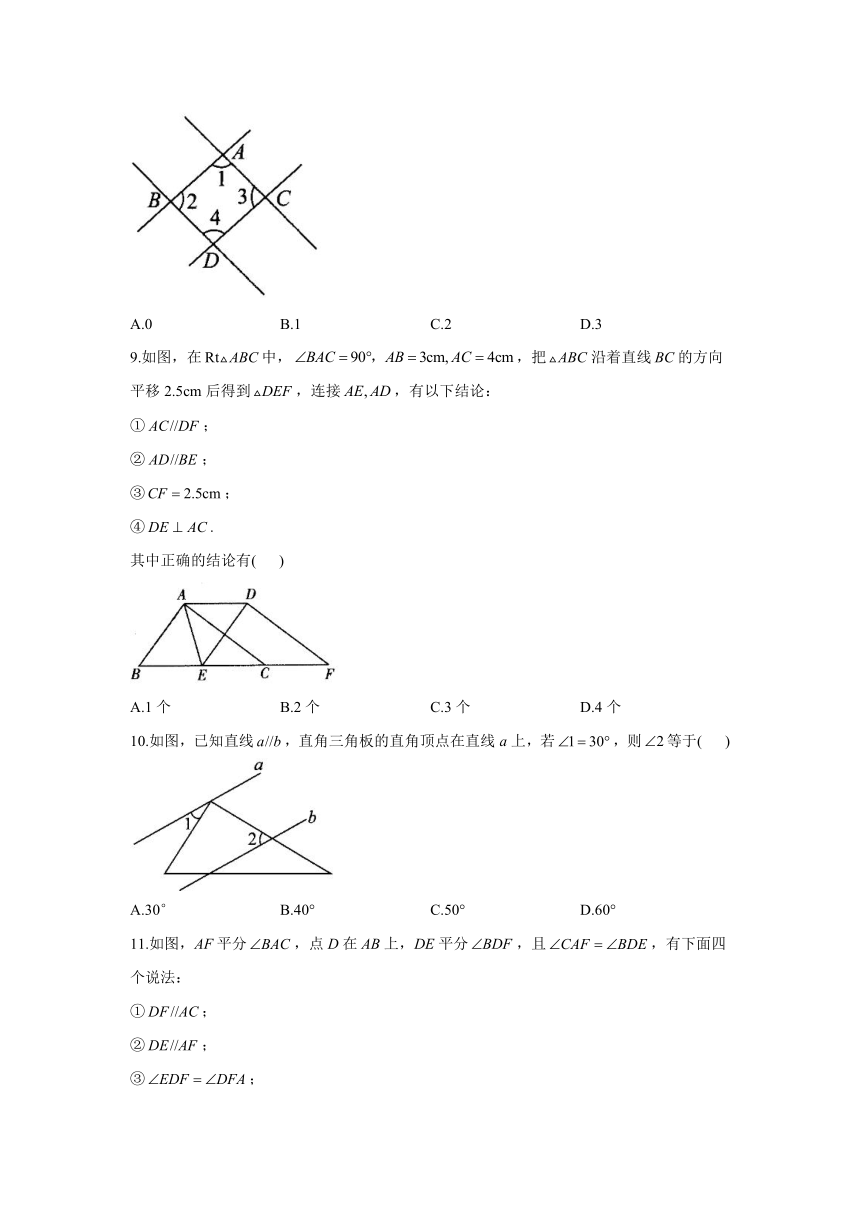
11.如图,AF平分,点D在AB上,DE平分,且,有下面四个说法:
①;
②;
③;
④.
其中正确的有(
)
A.①②③
B.①③④
C.①②④
D.①②③④
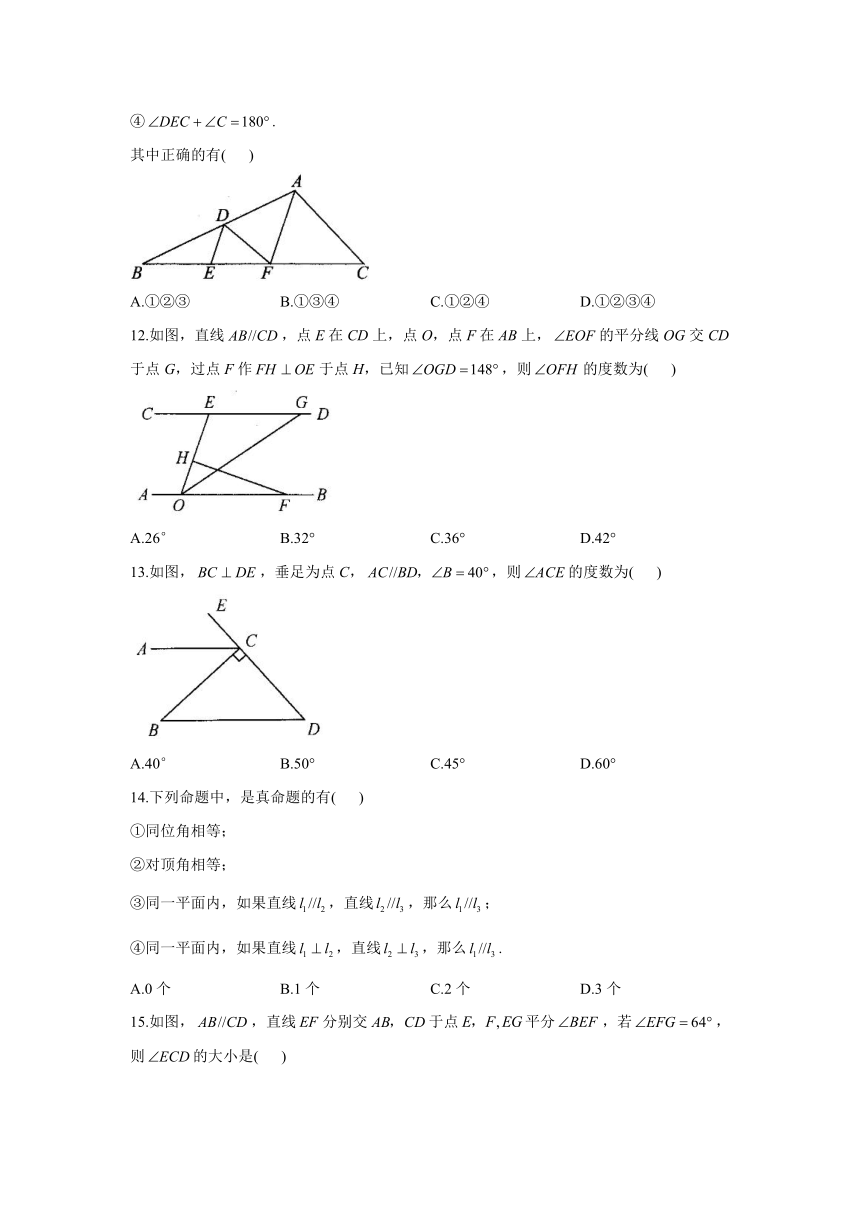
12.如图,直线,点E在CD上,点O,点F在AB上,的平分线OG交CD于点G,过点F作于点H,已知,则的度数为(
)
A.26°
B.32°
C.36°
D.42°
13.如图,,垂足为点C,,则的度数为(
)
A.40°
B.50°
C.45°
D.60°
14.下列命题中,是真命题的有(
)
①同位角相等;
②对顶角相等;
③同一平面内,如果直线,直线,那么;
④同一平面内,如果直线,直线,那么.
A.0个
B.1个
C.2个
D.3个
15.如图,,直线分别交于点平分,若,则的大小是(
)
A.132°
B.128°
C.122°
D.112°
16.如图所示,下列判断正确的是(
)
A.因为,所以
B.因为,所以
C.因为,所以
D.因为,所以
二、填空题(每空3分,共15分)
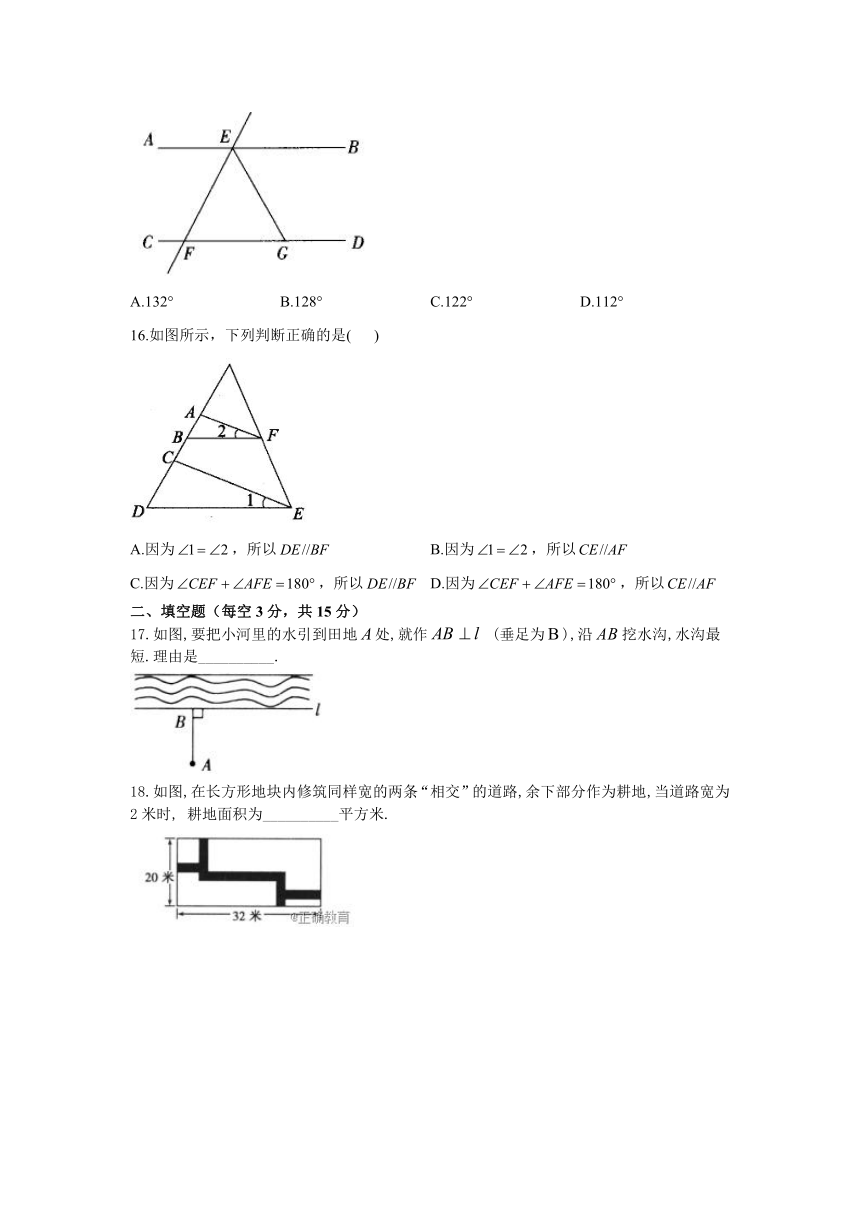
17.如图,要把小河里的水引到田地处,就作
(垂足为),沿挖水沟,水沟最短.理由是__________.
18.如图,在长方形地块内修筑同样宽的两条“相交”的道路,余下部分作为耕地,当道路宽为2米时,
耕地面积为__________平方米.
19、如图,
岛在
岛的北偏东
方向,
岛在
岛的北偏西
方向,则从
岛看
,
两岛的视角
等于
?????。
21.如图,已知,则、、三者之间的数量关系是????????????????
.
22.以下三种沿所在直线折叠纸带的方法:
(1)如图①,开后测得;
(2)如图②,展开后测得且;
(3)如图③,测得,
其中能判定纸带两条边线互相平行的是________(填序号).
三、简答题(共63分)
23.(9分)已知,如图,
,平分,平分,求证:
,完成下面的证明:
证明:∵
(已知)
?∴
(
???????????
???
)
又∵
(已知)?∴
(?????????????????
)
∵
(已知)?∴?????????????
(
????????????????
)
又∵平分
(已知)?∴______(??????????????????)
又∵平分
(已知)
∴??????????????
(?????????????????)
∴
(???????????????
+???????????
???
)?
∴
∴
(??????????????
????
)
即
24(10分).如图,在中,,将沿方向向右平移得到.
(1)试求出的度数;
(2)若请求出的长度.
25.(10分)如图,已知,
(1)证明:;
(2)若于点,且,求的度数.
26.(10分)如图5-6-10,,,,。
(1)求证:;
(2)连接,若平分,求的度数。
27.(12分)如图,直线、被直线所截,交点分别为、,平分,平分,如果,那么与平行吗?为什么?
28.(12分)
如图,已知
(1)求证:;
(2)若,分别平分,求的度数.
参考答案
1.答案:C
解析:根据对顶角的定义,A中和没有公共顶点,故不是对顶角;B中和两边不互为反向延长线,故不是对顶角;C中和有公共顶点,且两边互为反向延长线故为对顶角;D中和两边不互为反向延长线,故不是对顶角,故选C.
2.答案:A
解析:①电梯的升降,是平移;②照镜子,是轴对称;③钟表分针的运动,是旋转;④行驶中汽车车轮的运动,是旋转.故是平移现象的有1个.故选A.
3.答案:A
解析:在同一平面内,两条直线的位置关系有相交和平行两种.故选A.
4.答案:D
解析:对于A选项,由,可知,又平分,
,结论正确;对于B选项,与互为对顶角,,结论正确;对于C选项,与互为邻补角,结论正确;对于D选项,,的余角不等于故选D
5.答案:C
解析:,
又,
,故A结论正确
,
,故B结论正确
,
,故C结论不正确;
,
,故D结论正确。故选C
6.答案:C
解析:本题考查平行线的性质.如图,作直线又故选C.
7.答案:A
解析:由点的对应点的坐标是知,需将向右平移5个单位长度,再向上平移1个单位长度,则点的对应点的坐标为,点的对应点的坐标为.故选A.
8.答案:C
解析:因为,所以,所以.①错误.因为,所以,所以,所以.故②③正确.故选C.
9.答案:D
解析:沿着直线的方向平移2.5cm后得到,,故①正确;,故②正确;,故③正确;,,
,故④正确.故选D.
10.答案:D
解析:如图,因为直角三角板的直角顶点在直线a上,,所以.因为,所以.故选D.
11.答案:A
解析:因为AF平分,DE平分,所以.因为,所以.所以.所以.所以②,③正确;由上述推理知,,所以.所以,所以,所以①正确,④错误.故选A.
12.答案:A
解析:因为,所以,所以.因为OG平分,所以.因为,所以,所以.故选A.
13.答案:B
解析:因为,所以(两直线平行,内错角相等).因为,所以,所以.故选B.
14.答案:D
解析:①两直线平行,同位角相等,故①中的命题是假命题;②对顶角相等,是真命题;③同一平面内,如果直线,直线,那么,是真命题④同一平面内,如果直线,直线,那么,是真命题.综上,是真命题的有②③④,共3个,故选D.
15.答案:C
解析:,
,
平分,
,
.
故选C.
16.答案:D
解析:A,B两项中的不是两条直线被第三条直线所截而形成的角,故错误;C选项中的不是结论中的两条直线被第三条直线所截而形成的角,故错误;选项D根据“同旁内角互补,两直线平行”可判定,故正确.故选D.
17.答案:垂线段最短
解析:,垂足为,即从到的垂线段是,根据垂线段最短,知沿着挖水沟是最短的.
18.答案:540
解析:如图,根据平移可得,当道路宽为2米时,耕地的面积为
(平方米).
答案:
19、
解析:
本题考查了方位角的概念和平行线的性质根据方位角的概念和平行线的性质,结合三角形的内角和定理求解.如图
∵
岛在
岛的北偏东
方向,
,
∵
岛在
岛的北偏西
方向,
,
∵
,
,
,
20.答案:110
解析:延长与直线b相交,如图.
直线a平移后得到直线,
.
,而,
.故答案为110.
21.答案:
解析:∵,∴,
∵,∴,∵,
∴,
∴
22.答案:(1)(2)
解析:(1),根据内错角相等,两直线平行进行判定,故正确;
(2)且,由图可知,,
(内错角相等,两直线平行),故正确;
(3)测得,与既不是内错角也不是同位角
不能判定两直线平行,故错误
23.答案:证明:∵
(已知)
?∴
(两直线平行,内错角相等)
又∵
(已知)?∴
(两直线平行,内错角相等)
∵
(已知)?∴
(两直线平行,同旁内角互补)
又∵平分
(已知)?∴
(角平分线定义)
又∵平分
(已知)
∴
(
角平分线定义)
∴
(+)?
∴
∴
(等量代换)
即
24.答案:答案:(1)在中,,
.
由平移得.
(2)由平移得.
,
,
解析:
25.答案:(1)证明:
(2)
解析:
26.答案:(1)证明:,
,
,
,
又,
,
,
,
,
。
(2)平分,
,
,
,
。
解析:
27.答案:
∵
∴.
又平分,平分,
∴
∴
∴
解析:
29.(1)证明:过作,如图,则,
又,
.
(2)过作,如图分别平分
,,
,
学校:___________姓名:___________班级:___________考号:___________
一、单选题(1-10题每小题3分,11-26题每小题2分,共42分。)
1.下列图形中,和是对顶角的是(
)
A.
B.
C.
D.
2.下列各现象中:
①电梯的升降;
②照镜子;
③钟表分针的运动;
④行驶中汽车车轮的运动.
其中是平移现象的有(
)
A.1个
B.2个
C.3个
D.4个
3.在同一平面内,两条直线的位置关系有(
)
A.平行和相交
B.平行和垂直
C.平行、垂直和相交
D.垂直和相交
4.如图所示,直线相交于点,于点,平分,,则下列结论不正确的是(
)
A.
B.
C.与互为补角
D.的余角等于
5.将一副三角板按如图5-6-2所示的方式放置,下列结论中不正确的是(
)
A.若,则有
B.
C.若,则有
D.如果,必有
6.如图,直线则等于(
)
A.150°
B.180°
C.210°
D.240°
7.如图所示,在平面直角坐标系中,点的坐标分别为,将沿一确定方向平移得到,点B的对应点的坐标是则点的坐标分别是(
)
A.
B.
C.
D.
8.如图所示,若,则
①;
②;
③.
其中正确的个数为(
)
A.0
B.1
C.2
D.3
9.如图,在中,,把沿着直线的方向平移2.5cm后得到,连接,有以下结论:
①;
②;
③;
④.
其中正确的结论有(
)
A.1个
B.2个
C.3个
D.4个
10.如图,已知直线,直角三角板的直角顶点在直线a上,若,则等于(
)
A.30°
B.40°
C.50°
D.60°
11.如图,AF平分,点D在AB上,DE平分,且,有下面四个说法:
①;
②;
③;
④.
其中正确的有(
)
A.①②③
B.①③④
C.①②④
D.①②③④
12.如图,直线,点E在CD上,点O,点F在AB上,的平分线OG交CD于点G,过点F作于点H,已知,则的度数为(
)
A.26°
B.32°
C.36°
D.42°
13.如图,,垂足为点C,,则的度数为(
)
A.40°
B.50°
C.45°
D.60°
14.下列命题中,是真命题的有(
)
①同位角相等;
②对顶角相等;
③同一平面内,如果直线,直线,那么;
④同一平面内,如果直线,直线,那么.
A.0个
B.1个
C.2个
D.3个
15.如图,,直线分别交于点平分,若,则的大小是(
)
A.132°
B.128°
C.122°
D.112°
16.如图所示,下列判断正确的是(
)
A.因为,所以
B.因为,所以
C.因为,所以
D.因为,所以
二、填空题(每空3分,共15分)
17.如图,要把小河里的水引到田地处,就作
(垂足为),沿挖水沟,水沟最短.理由是__________.
18.如图,在长方形地块内修筑同样宽的两条“相交”的道路,余下部分作为耕地,当道路宽为2米时,
耕地面积为__________平方米.
19、如图,
岛在
岛的北偏东
方向,
岛在
岛的北偏西
方向,则从
岛看
,
两岛的视角
等于
?????。
21.如图,已知,则、、三者之间的数量关系是????????????????
.
22.以下三种沿所在直线折叠纸带的方法:
(1)如图①,开后测得;
(2)如图②,展开后测得且;
(3)如图③,测得,
其中能判定纸带两条边线互相平行的是________(填序号).
三、简答题(共63分)
23.(9分)已知,如图,
,平分,平分,求证:
,完成下面的证明:
证明:∵
(已知)
?∴
(
???????????
???
)
又∵
(已知)?∴
(?????????????????
)
∵
(已知)?∴?????????????
(
????????????????
)
又∵平分
(已知)?∴______(??????????????????)
又∵平分
(已知)
∴??????????????
(?????????????????)
∴
(???????????????
+???????????
???
)?
∴
∴
(??????????????
????
)
即
24(10分).如图,在中,,将沿方向向右平移得到.
(1)试求出的度数;
(2)若请求出的长度.
25.(10分)如图,已知,
(1)证明:;
(2)若于点,且,求的度数.
26.(10分)如图5-6-10,,,,。
(1)求证:;
(2)连接,若平分,求的度数。
27.(12分)如图,直线、被直线所截,交点分别为、,平分,平分,如果,那么与平行吗?为什么?
28.(12分)
如图,已知
(1)求证:;
(2)若,分别平分,求的度数.
参考答案
1.答案:C
解析:根据对顶角的定义,A中和没有公共顶点,故不是对顶角;B中和两边不互为反向延长线,故不是对顶角;C中和有公共顶点,且两边互为反向延长线故为对顶角;D中和两边不互为反向延长线,故不是对顶角,故选C.
2.答案:A
解析:①电梯的升降,是平移;②照镜子,是轴对称;③钟表分针的运动,是旋转;④行驶中汽车车轮的运动,是旋转.故是平移现象的有1个.故选A.
3.答案:A
解析:在同一平面内,两条直线的位置关系有相交和平行两种.故选A.
4.答案:D
解析:对于A选项,由,可知,又平分,
,结论正确;对于B选项,与互为对顶角,,结论正确;对于C选项,与互为邻补角,结论正确;对于D选项,,的余角不等于故选D
5.答案:C
解析:,
又,
,故A结论正确
,
,故B结论正确
,
,故C结论不正确;
,
,故D结论正确。故选C
6.答案:C
解析:本题考查平行线的性质.如图,作直线又故选C.
7.答案:A
解析:由点的对应点的坐标是知,需将向右平移5个单位长度,再向上平移1个单位长度,则点的对应点的坐标为,点的对应点的坐标为.故选A.
8.答案:C
解析:因为,所以,所以.①错误.因为,所以,所以,所以.故②③正确.故选C.
9.答案:D
解析:沿着直线的方向平移2.5cm后得到,,故①正确;,故②正确;,故③正确;,,
,故④正确.故选D.
10.答案:D
解析:如图,因为直角三角板的直角顶点在直线a上,,所以.因为,所以.故选D.
11.答案:A
解析:因为AF平分,DE平分,所以.因为,所以.所以.所以.所以②,③正确;由上述推理知,,所以.所以,所以,所以①正确,④错误.故选A.
12.答案:A
解析:因为,所以,所以.因为OG平分,所以.因为,所以,所以.故选A.
13.答案:B
解析:因为,所以(两直线平行,内错角相等).因为,所以,所以.故选B.
14.答案:D
解析:①两直线平行,同位角相等,故①中的命题是假命题;②对顶角相等,是真命题;③同一平面内,如果直线,直线,那么,是真命题④同一平面内,如果直线,直线,那么,是真命题.综上,是真命题的有②③④,共3个,故选D.
15.答案:C
解析:,
,
平分,
,
.
故选C.
16.答案:D
解析:A,B两项中的不是两条直线被第三条直线所截而形成的角,故错误;C选项中的不是结论中的两条直线被第三条直线所截而形成的角,故错误;选项D根据“同旁内角互补,两直线平行”可判定,故正确.故选D.
17.答案:垂线段最短
解析:,垂足为,即从到的垂线段是,根据垂线段最短,知沿着挖水沟是最短的.
18.答案:540
解析:如图,根据平移可得,当道路宽为2米时,耕地的面积为
(平方米).
答案:
19、
解析:
本题考查了方位角的概念和平行线的性质根据方位角的概念和平行线的性质,结合三角形的内角和定理求解.如图
∵
岛在
岛的北偏东
方向,
,
∵
岛在
岛的北偏西
方向,
,
∵
,
,
,
20.答案:110
解析:延长与直线b相交,如图.
直线a平移后得到直线,
.
,而,
.故答案为110.
21.答案:
解析:∵,∴,
∵,∴,∵,
∴,
∴
22.答案:(1)(2)
解析:(1),根据内错角相等,两直线平行进行判定,故正确;
(2)且,由图可知,,
(内错角相等,两直线平行),故正确;
(3)测得,与既不是内错角也不是同位角
不能判定两直线平行,故错误
23.答案:证明:∵
(已知)
?∴
(两直线平行,内错角相等)
又∵
(已知)?∴
(两直线平行,内错角相等)
∵
(已知)?∴
(两直线平行,同旁内角互补)
又∵平分
(已知)?∴
(角平分线定义)
又∵平分
(已知)
∴
(
角平分线定义)
∴
(+)?
∴
∴
(等量代换)
即
24.答案:答案:(1)在中,,
.
由平移得.
(2)由平移得.
,
,
解析:
25.答案:(1)证明:
(2)
解析:
26.答案:(1)证明:,
,
,
,
又,
,
,
,
,
。
(2)平分,
,
,
,
。
解析:
27.答案:
∵
∴.
又平分,平分,
∴
∴
∴
解析:
29.(1)证明:过作,如图,则,
又,
.
(2)过作,如图分别平分
,,
,
同课章节目录
