北师大版七年级下册数学《全等三角形》单元复习讲义 (2)
文档属性
| 名称 | 北师大版七年级下册数学《全等三角形》单元复习讲义 (2) |  | |
| 格式 | doc | ||
| 文件大小 | 340.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 08:45:22 | ||
图片预览


文档简介
教学内容 三角形全等的判定
教学目标 要求掌握三角形全等的判定定理,及应用条件
教学重点 三角形全等的证明
教学难点 三角形全等的证明
教学准备 讲义
教学过程
前课回顾
全等三角形复习(1) 知识点一:全等形的有关概念
1、全等形的定义:能够完全重合的两个图形叫做全等形.
2、全等三角形:能够完全重合的两个三角形叫做全等三角形.
3、对应顶点、对应边、对应角:把两个全等的三角形重合在一起,重合的顶点叫对应顶点;重合的边叫对应边,重合的角叫做对应角.
4、“全等”的符号:“≌”,读作“全等于”,记两个三角形全等时,通常把表示对应顶点的字母写在对应位置上.
知识点二:全等三角形的性质
全等三角形的对应边相等;全等三角形的对应角相等;全等三角形的周长、面积相等.
知识点三:全等三角形的判定方法
已知条件
证明思路
判定方法
简称
简写
适用对象
已知两边对应相等
找第三边
三边分别相等的两个三角形全等
边边边
SSS
所有三角形
找两边的夹角
两边和夹角分别相等的两个三角形全等
边角边
SAS
已知一边一角
找夹角的另一边
找夹边的另一角
两角和夹边分别相等的两个三角形全等
角边角
ASA
已知两角
找夹边
找任一角的对边
两角和其中一个角的对边分别相等的两个三角形全等
角角边
AAS
已知直角
找斜边与直角边
斜边和一条直角边分别相等的两个三角形全等
斜边直角边
HL
直角三角形
错题重现
例2:如图2,AB⊥BC,BC⊥CD,EB∥CF,则∠ABE与∠FCD的关系是( ) A.同位角且相等 B.不是同位角但相等
C.是同位角但不相等 D.不是同位角也不相等
练习13:如图18,l1// l2,则∠1+∠2-∠3= .
练习14:如图19,AB∥DE,那么∠BCD等于( )
A. ∠2-∠1 B. ∠1+∠2 C.180°+∠1-∠2 D.180°+∠2-2∠1
\\\\\
知识详解
例题1、如果ΔABC≌ΔDEF,则AB的对应边是_____,AC的对应边是_____,∠C的对应角是_____,∠DEF的对应角是_____.
2、如图1-1所示,ΔABC≌ΔDCB.(1)若∠D=74°∠DBC=38°,则∠A=_____,∠ABC=_____
(2)如果AC=DB,请指出其他的对应边________________________;
图1-1 图1-2 图1-3
3、如图1-2,已知△ABE≌△DCE,AE=2 cm,BE=1.5 cm,∠A=25°,∠B=48°;那么DE=_____cm,EC=_____cm,∠C=_____°;∠D=_____°.
4、如图1-3,△ABE和△ADC是△ABC分别沿着AB,AC翻折180°形成的若∠1∶∠2∶∠3=28∶5∶3,则∠α的度数为______.
练习1:如图1-4,△ABC≌△BAD,A和B、C和D是对应顶点,如果AB=5,BD=6,AD=4,那么BC等于 ( )
A.6 B.5 C.4 D.无法确定
2、如图1-5,△ABC≌△AEF,若∠ABC和∠AEF是对应角,则∠EAC等于 ( )
A.∠ACB B.∠CAF C.∠BAF D.∠BAC
3、如图1-6,△ABC≌ΔADE,若∠B=80°,∠C=30°,∠DAC=35°,则∠EAC的度数为 ( )
A.40° B.35° C.30° D.25°
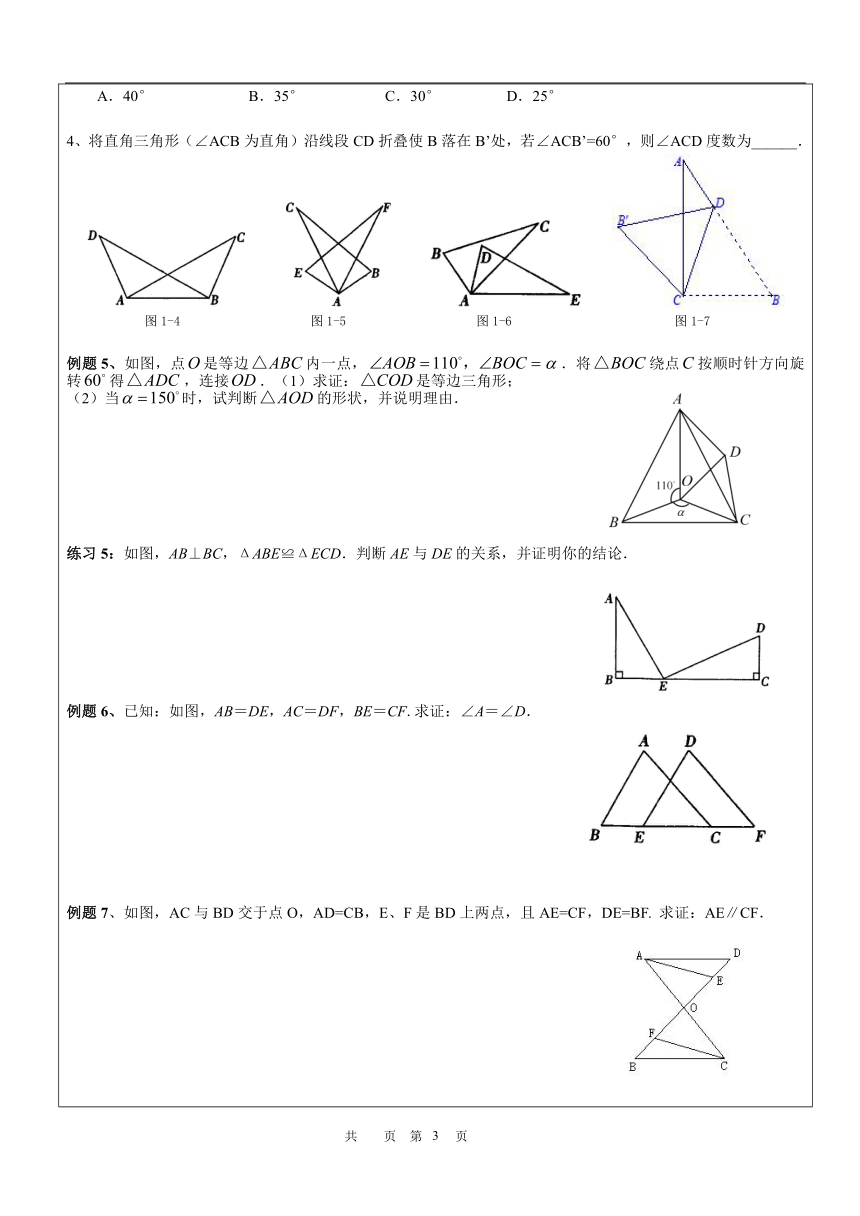
4、将直角三角形(∠ACB为直角)沿线段CD折叠使B落在B’处,若∠ACB’=60°,则∠ACD度数为______.
图1-4 图1-5 图1-6 图1-7
例题5、如图,点是等边内一点,.将绕点按顺时针方向旋转得,连接.(1)求证:是等边三角形;
(2)当时,试判断的形状,并说明理由.
练习5:如图,AB⊥BC,ΔABE≌ΔECD.判断AE与DE的关系,并证明你的结论.
例题6、已知:如图,AB=DE,AC=DF,BE=CF.求证:∠A=∠D.
例题7、如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF. 求证:AE∥CF.
练习6、已知:如图,AD=BC.AC=BD.试证明:∠CAD=∠DBC.
练习7、如图,CE=DE,EA=EB,CA=DB,求证:△ABC≌△BAD.
例题8、如图,Rt△ABC的斜边AB中点为E,ED⊥AB交BC于D,且∠CAD︰∠BAD=1︰7,求∠BAC的度数.
例题9、已知:如图,是和的平分线,.求证:.
练习8、如图,在△ABC中,DE垂直平分AB于E,交AC于D,若AB=AC=32,BC=21,求△BCD的周长.
9、如图,将两个一大、一小的等腰直角三角尺拼接 (A、B、D三点共线,AB=CB,EB=DB,∠ABC=∠EBD=90°),连接AE、CD,试确定AE与CD的位置与数量关系,并证明你的结论.
10、(综合练习)已知:如图,AB=DC,AE=DF,CE=FB,求证:AF=DE.
随堂检测
1、如图,AB=AC,AD = AE,CD=BE.求证:∠DAB=∠EAC.
2、已知:如图,AB∥CD,AB=CD.求证:AD∥BC.
3、如图,在△ABC中,AB=AC,D是BC的中点,连结AD,在AD的延长线上取一点E,连结BE,CE.求证:△ABE≌△ACE.
4、如图,在△ABC中,∠BAC=α(α>90°),PM、QN分别垂直平分AB、AC,垂足分别为M、N,交BC于P、Q,求∠PAQ的度数.
教学反思
3
共 页 第 页
教学目标 要求掌握三角形全等的判定定理,及应用条件
教学重点 三角形全等的证明
教学难点 三角形全等的证明
教学准备 讲义
教学过程
前课回顾
全等三角形复习(1) 知识点一:全等形的有关概念
1、全等形的定义:能够完全重合的两个图形叫做全等形.
2、全等三角形:能够完全重合的两个三角形叫做全等三角形.
3、对应顶点、对应边、对应角:把两个全等的三角形重合在一起,重合的顶点叫对应顶点;重合的边叫对应边,重合的角叫做对应角.
4、“全等”的符号:“≌”,读作“全等于”,记两个三角形全等时,通常把表示对应顶点的字母写在对应位置上.
知识点二:全等三角形的性质
全等三角形的对应边相等;全等三角形的对应角相等;全等三角形的周长、面积相等.
知识点三:全等三角形的判定方法
已知条件
证明思路
判定方法
简称
简写
适用对象
已知两边对应相等
找第三边
三边分别相等的两个三角形全等
边边边
SSS
所有三角形
找两边的夹角
两边和夹角分别相等的两个三角形全等
边角边
SAS
已知一边一角
找夹角的另一边
找夹边的另一角
两角和夹边分别相等的两个三角形全等
角边角
ASA
已知两角
找夹边
找任一角的对边
两角和其中一个角的对边分别相等的两个三角形全等
角角边
AAS
已知直角
找斜边与直角边
斜边和一条直角边分别相等的两个三角形全等
斜边直角边
HL
直角三角形
错题重现
例2:如图2,AB⊥BC,BC⊥CD,EB∥CF,则∠ABE与∠FCD的关系是( ) A.同位角且相等 B.不是同位角但相等
C.是同位角但不相等 D.不是同位角也不相等
练习13:如图18,l1// l2,则∠1+∠2-∠3= .
练习14:如图19,AB∥DE,那么∠BCD等于( )
A. ∠2-∠1 B. ∠1+∠2 C.180°+∠1-∠2 D.180°+∠2-2∠1
\\\\\
知识详解
例题1、如果ΔABC≌ΔDEF,则AB的对应边是_____,AC的对应边是_____,∠C的对应角是_____,∠DEF的对应角是_____.
2、如图1-1所示,ΔABC≌ΔDCB.(1)若∠D=74°∠DBC=38°,则∠A=_____,∠ABC=_____
(2)如果AC=DB,请指出其他的对应边________________________;
图1-1 图1-2 图1-3
3、如图1-2,已知△ABE≌△DCE,AE=2 cm,BE=1.5 cm,∠A=25°,∠B=48°;那么DE=_____cm,EC=_____cm,∠C=_____°;∠D=_____°.
4、如图1-3,△ABE和△ADC是△ABC分别沿着AB,AC翻折180°形成的若∠1∶∠2∶∠3=28∶5∶3,则∠α的度数为______.
练习1:如图1-4,△ABC≌△BAD,A和B、C和D是对应顶点,如果AB=5,BD=6,AD=4,那么BC等于 ( )
A.6 B.5 C.4 D.无法确定
2、如图1-5,△ABC≌△AEF,若∠ABC和∠AEF是对应角,则∠EAC等于 ( )
A.∠ACB B.∠CAF C.∠BAF D.∠BAC
3、如图1-6,△ABC≌ΔADE,若∠B=80°,∠C=30°,∠DAC=35°,则∠EAC的度数为 ( )
A.40° B.35° C.30° D.25°
4、将直角三角形(∠ACB为直角)沿线段CD折叠使B落在B’处,若∠ACB’=60°,则∠ACD度数为______.
图1-4 图1-5 图1-6 图1-7
例题5、如图,点是等边内一点,.将绕点按顺时针方向旋转得,连接.(1)求证:是等边三角形;
(2)当时,试判断的形状,并说明理由.
练习5:如图,AB⊥BC,ΔABE≌ΔECD.判断AE与DE的关系,并证明你的结论.
例题6、已知:如图,AB=DE,AC=DF,BE=CF.求证:∠A=∠D.
例题7、如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF. 求证:AE∥CF.
练习6、已知:如图,AD=BC.AC=BD.试证明:∠CAD=∠DBC.
练习7、如图,CE=DE,EA=EB,CA=DB,求证:△ABC≌△BAD.
例题8、如图,Rt△ABC的斜边AB中点为E,ED⊥AB交BC于D,且∠CAD︰∠BAD=1︰7,求∠BAC的度数.
例题9、已知:如图,是和的平分线,.求证:.
练习8、如图,在△ABC中,DE垂直平分AB于E,交AC于D,若AB=AC=32,BC=21,求△BCD的周长.
9、如图,将两个一大、一小的等腰直角三角尺拼接 (A、B、D三点共线,AB=CB,EB=DB,∠ABC=∠EBD=90°),连接AE、CD,试确定AE与CD的位置与数量关系,并证明你的结论.
10、(综合练习)已知:如图,AB=DC,AE=DF,CE=FB,求证:AF=DE.
随堂检测
1、如图,AB=AC,AD = AE,CD=BE.求证:∠DAB=∠EAC.
2、已知:如图,AB∥CD,AB=CD.求证:AD∥BC.
3、如图,在△ABC中,AB=AC,D是BC的中点,连结AD,在AD的延长线上取一点E,连结BE,CE.求证:△ABE≌△ACE.
4、如图,在△ABC中,∠BAC=α(α>90°),PM、QN分别垂直平分AB、AC,垂足分别为M、N,交BC于P、Q,求∠PAQ的度数.
教学反思
3
共 页 第 页
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
