北师大版七年级下册数学《全等三角形》单元复习讲义(无答案)
文档属性
| 名称 | 北师大版七年级下册数学《全等三角形》单元复习讲义(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 257.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-01 18:13:06 | ||
图片预览

文档简介
教学内容 三角形全等证明提高
教学目标 掌握三角形全等的性质及判定
教学重点 三角形全等的证明
教学难点 辅助线的做法及三角形全等的方法
教学准备 讲义
教学过程
前课回顾
一、全等三角形 1.判定和性质
一般三角形
直角三角形
判定
边角边(SAS)、角边角(ASA)
角角边(AAS)、边边边(SSS)
具备一般三角形的判定方法
斜边和一条直角边对应相等(HL)
性质
对应边相等,对应角相等
对应中线相等,对应高相等,对应角平分线相等
注:① 判定两个三角形全等必须有一组边对应相等;
② 全等三角形面积相等.
2.证题的思路:
知识详解
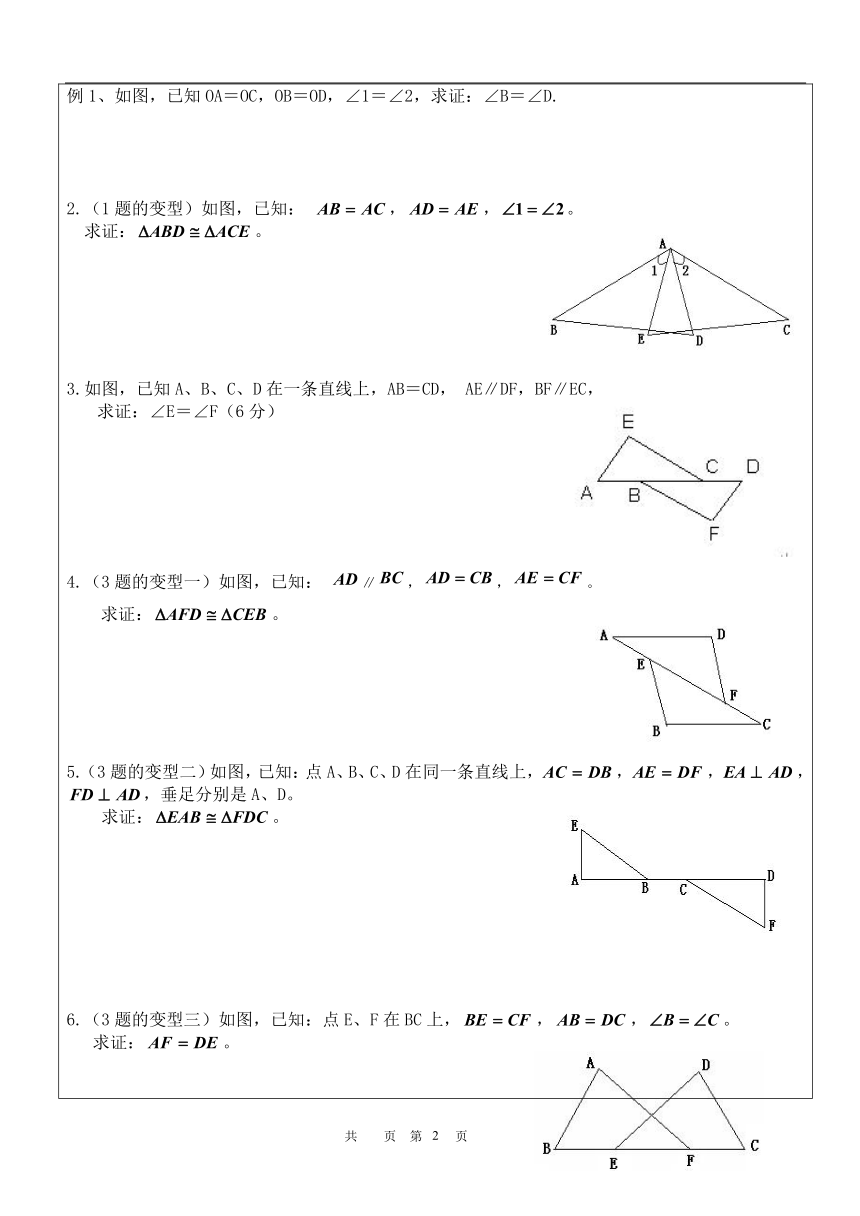
例1、如图,已知OA=OC,OB=OD,∠1=∠2,求证:∠B=∠D.
2.(1题的变型)如图,已知: ,,。
求证:。
3.如图,已知A、B、C、D在一条直线上,AB=CD, AE∥DF,BF∥EC,
求证:∠E=∠F(6分)
4.(3题的变型一)如图,已知: ∥,,。
求证:。
5.(3题的变型二)如图,已知:点A、B、C、D在同一条直线上,,,,,垂足分别是A、D。
求证:。
6.(3题的变型三)如图,已知:点E、F在BC上,,,。
求证:。
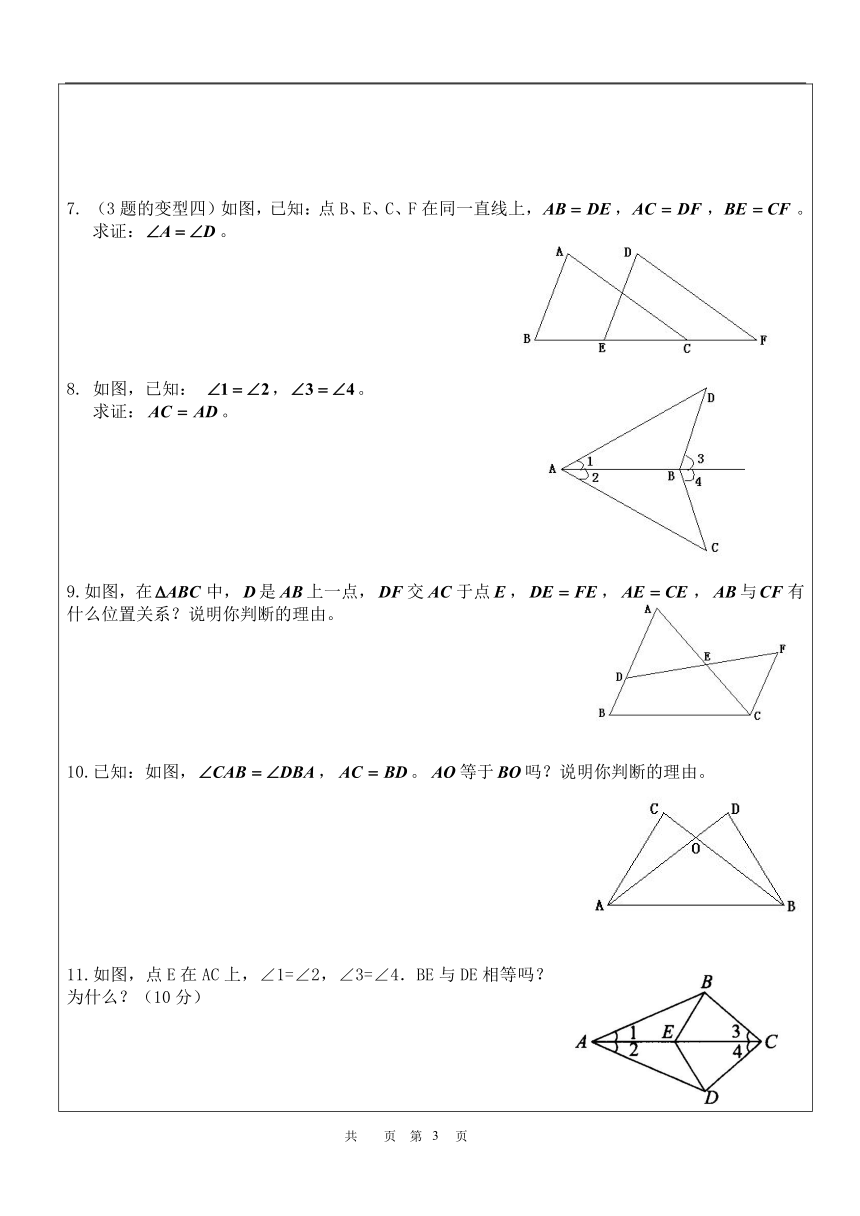
7. (3题的变型四)如图,已知:点B、E、C、F在同一直线上,,,。
求证:。
8. 如图,已知: ,。
求证:。
9.如图,在中,是上一点,交于点,,,与有什么位置关系?说明你判断的理由。
10.已知:如图,,。等于吗?说明你判断的理由。
11.如图,点E在AC上,∠1=∠2,∠3=∠4.BE与DE相等吗?为什么?(10分)
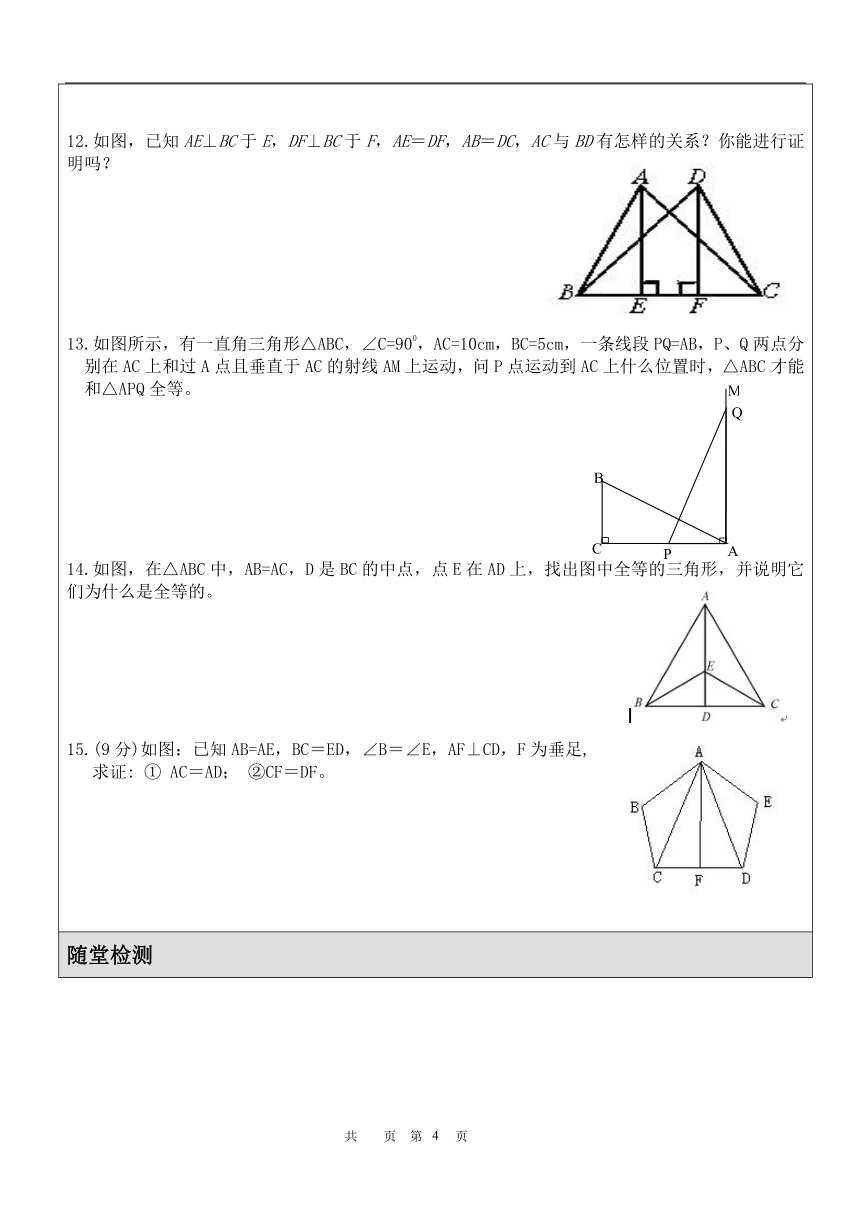
12.如图,已知AE⊥BC于E,DF⊥BC于F,AE=DF,AB=DC,AC与BD有怎样的关系?你能进行证明吗?
13.如图所示,有一直角三角形△ABC,∠C=900,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线AM上运动,问P点运动到AC上什么位置时,△ABC才能和△APQ全等。
14.如图,在△ABC中,AB=AC,D是BC的中点,点E在AD上,找出图中全等的三角形,并说明它们为什么是全等的。
15.(9分)如图:已知AB=AE,BC=ED,∠B=∠E,AF⊥CD,F为垂足,
求证: ① AC=AD; ②CF=DF。
随堂检测
一.选择题(共25小题)
1.(2015春?衡阳县期末)下列条件中能组成三角形的是( )
A.7cm,7cm,12cm B.5cm,3cm,9cm C.6cm,9cm,16cm D.5cm,6cm,11cm
2.(2015春?大渡口区期末)已知三角形三边长分别是1、x、2,且x为整数,那么x的取值是( )
A.x=1 B.x=2 C.x=3 D.x=4
3.(2015?泉州)已知△ABC中,AB=6,BC=4,那么边AC的长可能是下列哪个值( )
A.11 B.5 C.2 D.1
4.(2016?大埔县一模)已知△ABC中,D,E分别是AC,AB边上的中点,BD⊥CE于点F,CE=2,BD=4,则△ABC的面积为( )
A. B.8 C.4 D.6
5.(2016春?宜兴市校级月考)如图,BE是∠ABD的平分线,CF是∠ACD的平分线,BE与CF交于G,若∠BDC=140°,∠BGC=110°,则∠A为( )
A.70° B.75° C.80° D.85°
6.(2015?荆门)如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:
①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,
其中结论正确的有( )
A.1个 B.2个 C.3个 D.4个
7.(2014?山西)如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为( )
A.a2 B.a2 C.a2 D.a2
8.(2011?临川区模拟)两本书按如图所示方式叠放在一起,则图中相等的角是( )
A.∠1与∠2 B.∠2与∠3 C.∠1与∠3 D.三个角都相等
9.(2005?广州)如图,已知点A(﹣1,0)和点B(1,2),在坐标轴上确定点P,使得△ABP为直角三角形,则满足这样条件的点P共有( )
A.2个 B.4个 C.6个 D.7个
10.(2015秋?河东区期末)如图,已知BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是( )
A.2 B.3 C.6 D.不能确定
11.(2015春?昌邑市期末)如图,在△ABC中,∠ABC=60°,∠ACB=80°,BP平分∠ABC,CP平分∠ACB,则∠BPC的大小是( )
A.100° B.110° C.115° D.120°
12.(2015秋?南开区期末)在△ABC和△A′B′C′中,已知∠A=∠A′,AB=A′B′,添加下列条件中的一个,不能使△ABC≌△A′B′C′一定成立的是( )
A.AC=A′C′ B.BC=B′C′ C.∠B=∠B′ D.∠C=∠C′
13.(2015春?禅城区校级期末)下列条件中能判定△ABC≌△DEF的是( )
A.AB=DE,BC=EF,∠A=∠D B.∠A=∠D,∠B=∠E,∠C=∠F
C.AC=DF,∠B=∠F,AB=DE D.∠B=∠E,∠C=∠F,AC=DF
14.(2015秋?南陵县期末)如图,四边形ABCD中,AB∥CD,BC∥AD,点E、F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
A.∠1=∠2 B.BF=DE C.AE=CF D.∠AED=∠CFB
15.(2015秋?重庆校级期末)如图,AC平分∠DAB,AD=AC=AB,如下四个结论:①AC⊥BD;②BC=DE;③∠DBC=∠DAC;④△ABC是正三角形,正确的结论有( )
A.1个 B.2个 C.3个 D.4个
16.(2015秋?西宁校级期中)如图,已知AB、CD相交于O点,△AOC≌△BOD,E、F分别在OA、OB上,要使△EOC≌△FOD,添加的一个条件不可以是( )
A.CE=DF B.∠CEA=∠DFB C.∠OCE=∠ODF D.OE=OF
17.(2015秋?海安县校级月考)根据下列条件能画出唯一△ABC的是( )
A.AB=3,BC=4,AC=8 B.AB=4,BC=3,∠A=30°
C.∠A=30°,∠B=70°,∠C=80° D.∠A=60°,∠B=30°,AB=4
18.(2015秋?萧山区期中)已知△ABC是等边三角形,点D、E分别在AC、BC边上,且AD=CE,AE与BD交于点F,则∠AFD的度数为( )
A.60° B.45° C.75° D.70°
19.(2015秋?北京校级期中)在数学活动课上,小明提出这样一个问题:如右图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB的度数是( )
A.65° B.55° C.45° D.35°
20.(2015秋?南宁校级月考)如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
A.90° B.180° C.270° D.360°
21.(2015秋?冠县月考)在△ABC和△EMN中,已知∠A=50°,∠B=60°,∠E=70°,∠M=60°,AC=EN,则这两个三角形( )
A.一定全等 B.一定不全等 C.不一定全等 D.以上都不对
22.(2012?柳州)如图,小强利用全等三角形的知识测量池塘两端M、N的距离,如果△PQO≌△NMO,则只需测出其长度的线段是( )
A.PO B.PQ C.MO D.MQ
23.(2011春?苏州期末)小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃?应该带( )去.
A.第1块 B.第2块 C.第3块 D.第4块
24.(2009秋?邹城市期末)长为3cm,4cm,6cm,8cm的木条各两根,小明与小刚分别取了3cm和4cm的两根,要使两人所拿的三根木条组成的两个三角形全等,则他俩取的第三根木条应为( )
A.一个人取6cm的木条,一个人取8cm的木条
B.两人都取6cm的木条
C.两人都取8cm的木条
D.C两种取法都可以
25.如图,设在一个宽度为w的小巷内,一个梯子长为a,梯子的脚位于A点,将梯子的顶端放在一堵墙上Q点时,Q离开地面的高度为k,梯子的倾斜角为45°;将该梯子的顶端放在另一堵墙上R点时,R点离开地面的高度为h,且此时梯子倾斜角为75°,则小巷宽度w=( )
A.h B.k C.a D.
3
共 页 第 页
教学目标 掌握三角形全等的性质及判定
教学重点 三角形全等的证明
教学难点 辅助线的做法及三角形全等的方法
教学准备 讲义
教学过程
前课回顾
一、全等三角形 1.判定和性质
一般三角形
直角三角形
判定
边角边(SAS)、角边角(ASA)
角角边(AAS)、边边边(SSS)
具备一般三角形的判定方法
斜边和一条直角边对应相等(HL)
性质
对应边相等,对应角相等
对应中线相等,对应高相等,对应角平分线相等
注:① 判定两个三角形全等必须有一组边对应相等;
② 全等三角形面积相等.
2.证题的思路:
知识详解
例1、如图,已知OA=OC,OB=OD,∠1=∠2,求证:∠B=∠D.
2.(1题的变型)如图,已知: ,,。
求证:。
3.如图,已知A、B、C、D在一条直线上,AB=CD, AE∥DF,BF∥EC,
求证:∠E=∠F(6分)
4.(3题的变型一)如图,已知: ∥,,。
求证:。
5.(3题的变型二)如图,已知:点A、B、C、D在同一条直线上,,,,,垂足分别是A、D。
求证:。
6.(3题的变型三)如图,已知:点E、F在BC上,,,。
求证:。
7. (3题的变型四)如图,已知:点B、E、C、F在同一直线上,,,。
求证:。
8. 如图,已知: ,。
求证:。
9.如图,在中,是上一点,交于点,,,与有什么位置关系?说明你判断的理由。
10.已知:如图,,。等于吗?说明你判断的理由。
11.如图,点E在AC上,∠1=∠2,∠3=∠4.BE与DE相等吗?为什么?(10分)
12.如图,已知AE⊥BC于E,DF⊥BC于F,AE=DF,AB=DC,AC与BD有怎样的关系?你能进行证明吗?
13.如图所示,有一直角三角形△ABC,∠C=900,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线AM上运动,问P点运动到AC上什么位置时,△ABC才能和△APQ全等。
14.如图,在△ABC中,AB=AC,D是BC的中点,点E在AD上,找出图中全等的三角形,并说明它们为什么是全等的。
15.(9分)如图:已知AB=AE,BC=ED,∠B=∠E,AF⊥CD,F为垂足,
求证: ① AC=AD; ②CF=DF。
随堂检测
一.选择题(共25小题)
1.(2015春?衡阳县期末)下列条件中能组成三角形的是( )
A.7cm,7cm,12cm B.5cm,3cm,9cm C.6cm,9cm,16cm D.5cm,6cm,11cm
2.(2015春?大渡口区期末)已知三角形三边长分别是1、x、2,且x为整数,那么x的取值是( )
A.x=1 B.x=2 C.x=3 D.x=4
3.(2015?泉州)已知△ABC中,AB=6,BC=4,那么边AC的长可能是下列哪个值( )
A.11 B.5 C.2 D.1
4.(2016?大埔县一模)已知△ABC中,D,E分别是AC,AB边上的中点,BD⊥CE于点F,CE=2,BD=4,则△ABC的面积为( )
A. B.8 C.4 D.6
5.(2016春?宜兴市校级月考)如图,BE是∠ABD的平分线,CF是∠ACD的平分线,BE与CF交于G,若∠BDC=140°,∠BGC=110°,则∠A为( )
A.70° B.75° C.80° D.85°
6.(2015?荆门)如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:
①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,
其中结论正确的有( )
A.1个 B.2个 C.3个 D.4个
7.(2014?山西)如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为( )
A.a2 B.a2 C.a2 D.a2
8.(2011?临川区模拟)两本书按如图所示方式叠放在一起,则图中相等的角是( )
A.∠1与∠2 B.∠2与∠3 C.∠1与∠3 D.三个角都相等
9.(2005?广州)如图,已知点A(﹣1,0)和点B(1,2),在坐标轴上确定点P,使得△ABP为直角三角形,则满足这样条件的点P共有( )
A.2个 B.4个 C.6个 D.7个
10.(2015秋?河东区期末)如图,已知BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是( )
A.2 B.3 C.6 D.不能确定
11.(2015春?昌邑市期末)如图,在△ABC中,∠ABC=60°,∠ACB=80°,BP平分∠ABC,CP平分∠ACB,则∠BPC的大小是( )
A.100° B.110° C.115° D.120°
12.(2015秋?南开区期末)在△ABC和△A′B′C′中,已知∠A=∠A′,AB=A′B′,添加下列条件中的一个,不能使△ABC≌△A′B′C′一定成立的是( )
A.AC=A′C′ B.BC=B′C′ C.∠B=∠B′ D.∠C=∠C′
13.(2015春?禅城区校级期末)下列条件中能判定△ABC≌△DEF的是( )
A.AB=DE,BC=EF,∠A=∠D B.∠A=∠D,∠B=∠E,∠C=∠F
C.AC=DF,∠B=∠F,AB=DE D.∠B=∠E,∠C=∠F,AC=DF
14.(2015秋?南陵县期末)如图,四边形ABCD中,AB∥CD,BC∥AD,点E、F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
A.∠1=∠2 B.BF=DE C.AE=CF D.∠AED=∠CFB
15.(2015秋?重庆校级期末)如图,AC平分∠DAB,AD=AC=AB,如下四个结论:①AC⊥BD;②BC=DE;③∠DBC=∠DAC;④△ABC是正三角形,正确的结论有( )
A.1个 B.2个 C.3个 D.4个
16.(2015秋?西宁校级期中)如图,已知AB、CD相交于O点,△AOC≌△BOD,E、F分别在OA、OB上,要使△EOC≌△FOD,添加的一个条件不可以是( )
A.CE=DF B.∠CEA=∠DFB C.∠OCE=∠ODF D.OE=OF
17.(2015秋?海安县校级月考)根据下列条件能画出唯一△ABC的是( )
A.AB=3,BC=4,AC=8 B.AB=4,BC=3,∠A=30°
C.∠A=30°,∠B=70°,∠C=80° D.∠A=60°,∠B=30°,AB=4
18.(2015秋?萧山区期中)已知△ABC是等边三角形,点D、E分别在AC、BC边上,且AD=CE,AE与BD交于点F,则∠AFD的度数为( )
A.60° B.45° C.75° D.70°
19.(2015秋?北京校级期中)在数学活动课上,小明提出这样一个问题:如右图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB的度数是( )
A.65° B.55° C.45° D.35°
20.(2015秋?南宁校级月考)如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
A.90° B.180° C.270° D.360°
21.(2015秋?冠县月考)在△ABC和△EMN中,已知∠A=50°,∠B=60°,∠E=70°,∠M=60°,AC=EN,则这两个三角形( )
A.一定全等 B.一定不全等 C.不一定全等 D.以上都不对
22.(2012?柳州)如图,小强利用全等三角形的知识测量池塘两端M、N的距离,如果△PQO≌△NMO,则只需测出其长度的线段是( )
A.PO B.PQ C.MO D.MQ
23.(2011春?苏州期末)小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃?应该带( )去.
A.第1块 B.第2块 C.第3块 D.第4块
24.(2009秋?邹城市期末)长为3cm,4cm,6cm,8cm的木条各两根,小明与小刚分别取了3cm和4cm的两根,要使两人所拿的三根木条组成的两个三角形全等,则他俩取的第三根木条应为( )
A.一个人取6cm的木条,一个人取8cm的木条
B.两人都取6cm的木条
C.两人都取8cm的木条
D.C两种取法都可以
25.如图,设在一个宽度为w的小巷内,一个梯子长为a,梯子的脚位于A点,将梯子的顶端放在一堵墙上Q点时,Q离开地面的高度为k,梯子的倾斜角为45°;将该梯子的顶端放在另一堵墙上R点时,R点离开地面的高度为h,且此时梯子倾斜角为75°,则小巷宽度w=( )
A.h B.k C.a D.
3
共 页 第 页
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
