北师大版七年级下册数学《全等三角形》复习(2)讲义
文档属性
| 名称 | 北师大版七年级下册数学《全等三角形》复习(2)讲义 |
|
|
| 格式 | doc | ||
| 文件大小 | 228.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-01 00:00:00 | ||
图片预览

文档简介
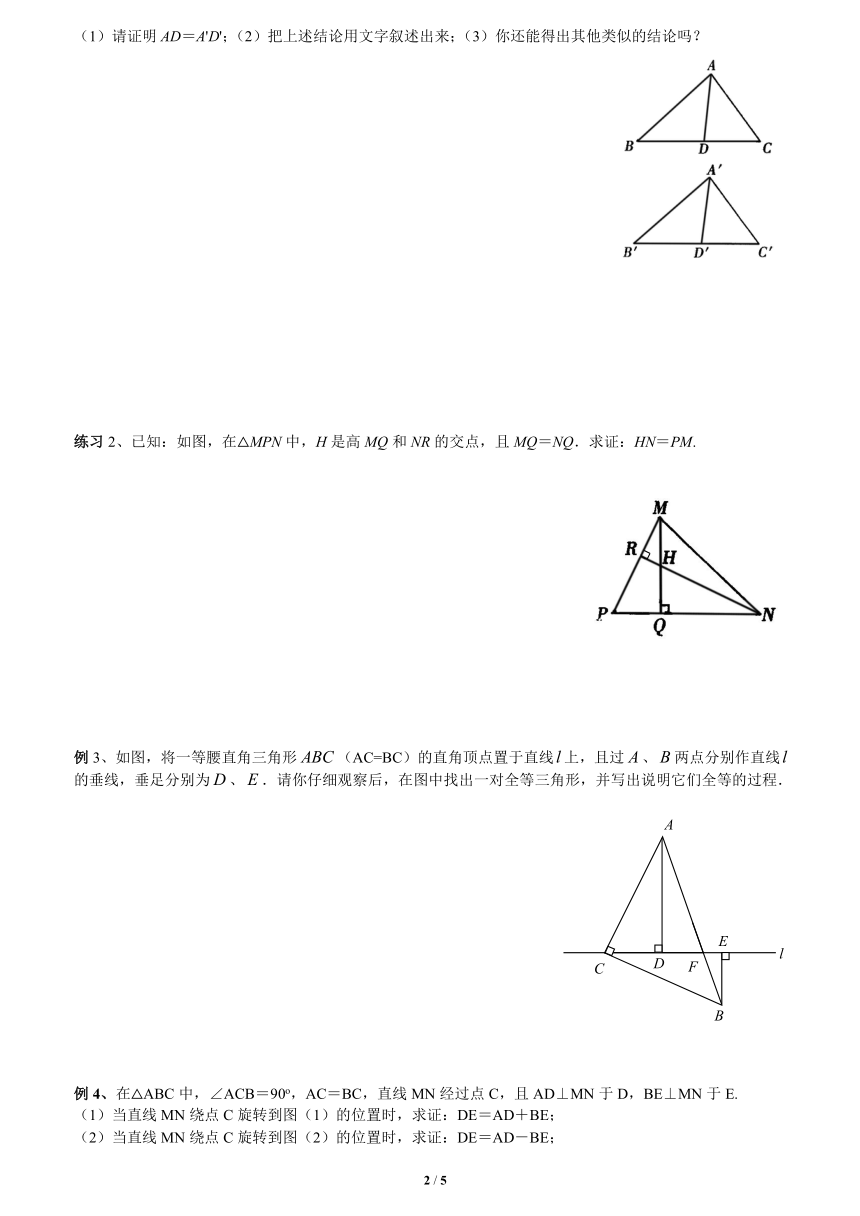
12.2全等三角形复习(2)
知识点一:全等三角形的判定
1、全等三角形的判定三:两角和它们的夹边对应相等的两个三角形全等,简_???_为“角边角”或“ASA”.
用数学语言表述:在△ABC和中,
∵ ∴△ABC≌(ASA)
2、全等三角形的判定四:两个角和其中一个角的对边对应相等的两个三角形全等,简_???_为“角角边”或“AAS”.
用数学语言表述:在△ABC和中,
∵ ∴△ABC≌(AAS)
3、直角三角形全等的判定:斜边和一条直角边对应相等的两个直角三角形全等,简_???_为“斜边直角边”或“HL”.
用数学语言表述:
在Rt△ABC和Rt中,
∵ ∴Rt△ABC≌Rt(HL)
例1、已知:如图,PM=PN,∠M=∠N.求证:AM=BN.
例2、如图,在△ABC中,MN⊥AC,垂足为N,且MN平分∠AMC,△ABM的周长为9cm,AN=2cm,求△ABC的周长.
练习1、如图,已知ΔABC≌ΔA'B'C',AD、A'D'分别是ΔABC和ΔA'B'C'的角平分线.
(1)请证明AD=A'D';(2)把上述结论用文字叙述出来;(3)你还能得出其他类似的结论吗?
练习2、已知:如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ.求证:HN=PM.
例3、如图,将一等腰直角三角形(AC=BC)的直角顶点置于直线上,且过、两点分别作直线的垂线,垂足分别为、.请你仔细观察后,在图中找出一对全等三角形,并写出说明它们全等的过程.
例4、在△ABC中,∠ACB=90o,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图(1)的位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到图(2)的位置时,求证:DE=AD-BE;
(3)当直线MN绕点C旋转到图(3)的位置时,试问DE、AD、BE具有怎样的等量关系?请直接写出这个等量关系.
练习3、已知:如图,AB⊥AE,AD⊥AC,∠E=∠B,DE=CB.求证:AD=AC.
练习4、如图所示,△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE, 垂足为F,过B作BD⊥BC交CF的延长线于D,求证:(1)AE=CD;(2)若AC=12cm,求BD的长.
例5、已知:如图,AE⊥AB,BC⊥AB,AE=AB,ED=AC.求证:ED⊥AC.
练习5、已知:如图,DE⊥AC,BF⊥AC,AD=BC,DE=BF.求证:AB∥DC.
课 后 作 业
1、阅读下题及一位同学的解答过程:如图4-10,AB和CD相交于点O,且OA=OB,∠A=∠C.那么△AOD与△COB全等吗?若全等,试写出证明过程;若不全等,请说明理由.
答:△AOD≌△COB.
证明:在△AOD和△COB中,
∴ △AOD≌△COB (ASA).
问:这位同学的回答及证明过程正确吗?为什么?
2、如图:已知AE交BC于点D,∠1=∠2=∠3, AB=AD. 求证:DC=BE.
3、(1)已知:如图,线段AC、BD交于O,∠AOB为钝角,AB=CD,BF⊥AC于F,DE⊥AC于E,AE=CF.求证:BO=DO.
(2)若∠AOB为锐角,其他条件不变,请画出图形并判断 (1)中的结论是否仍然成立?若成立,请加以证明;若不成立,请说明理由.
4、在一池塘边有A、B两棵树,如图7-4.试设计一种方案,测量A、B两棵树之间的距离.
6 / 6
知识点一:全等三角形的判定
1、全等三角形的判定三:两角和它们的夹边对应相等的两个三角形全等,简_???_为“角边角”或“ASA”.
用数学语言表述:在△ABC和中,
∵ ∴△ABC≌(ASA)
2、全等三角形的判定四:两个角和其中一个角的对边对应相等的两个三角形全等,简_???_为“角角边”或“AAS”.
用数学语言表述:在△ABC和中,
∵ ∴△ABC≌(AAS)
3、直角三角形全等的判定:斜边和一条直角边对应相等的两个直角三角形全等,简_???_为“斜边直角边”或“HL”.
用数学语言表述:
在Rt△ABC和Rt中,
∵ ∴Rt△ABC≌Rt(HL)
例1、已知:如图,PM=PN,∠M=∠N.求证:AM=BN.
例2、如图,在△ABC中,MN⊥AC,垂足为N,且MN平分∠AMC,△ABM的周长为9cm,AN=2cm,求△ABC的周长.
练习1、如图,已知ΔABC≌ΔA'B'C',AD、A'D'分别是ΔABC和ΔA'B'C'的角平分线.
(1)请证明AD=A'D';(2)把上述结论用文字叙述出来;(3)你还能得出其他类似的结论吗?
练习2、已知:如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ.求证:HN=PM.
例3、如图,将一等腰直角三角形(AC=BC)的直角顶点置于直线上,且过、两点分别作直线的垂线,垂足分别为、.请你仔细观察后,在图中找出一对全等三角形,并写出说明它们全等的过程.
例4、在△ABC中,∠ACB=90o,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图(1)的位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到图(2)的位置时,求证:DE=AD-BE;
(3)当直线MN绕点C旋转到图(3)的位置时,试问DE、AD、BE具有怎样的等量关系?请直接写出这个等量关系.
练习3、已知:如图,AB⊥AE,AD⊥AC,∠E=∠B,DE=CB.求证:AD=AC.
练习4、如图所示,△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE, 垂足为F,过B作BD⊥BC交CF的延长线于D,求证:(1)AE=CD;(2)若AC=12cm,求BD的长.
例5、已知:如图,AE⊥AB,BC⊥AB,AE=AB,ED=AC.求证:ED⊥AC.
练习5、已知:如图,DE⊥AC,BF⊥AC,AD=BC,DE=BF.求证:AB∥DC.
课 后 作 业
1、阅读下题及一位同学的解答过程:如图4-10,AB和CD相交于点O,且OA=OB,∠A=∠C.那么△AOD与△COB全等吗?若全等,试写出证明过程;若不全等,请说明理由.
答:△AOD≌△COB.
证明:在△AOD和△COB中,
∴ △AOD≌△COB (ASA).
问:这位同学的回答及证明过程正确吗?为什么?
2、如图:已知AE交BC于点D,∠1=∠2=∠3, AB=AD. 求证:DC=BE.
3、(1)已知:如图,线段AC、BD交于O,∠AOB为钝角,AB=CD,BF⊥AC于F,DE⊥AC于E,AE=CF.求证:BO=DO.
(2)若∠AOB为锐角,其他条件不变,请画出图形并判断 (1)中的结论是否仍然成立?若成立,请加以证明;若不成立,请说明理由.
4、在一池塘边有A、B两棵树,如图7-4.试设计一种方案,测量A、B两棵树之间的距离.
6 / 6
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
