北师大版七年级下册数学《全等三角形》复习讲义 (3)(无答案)
文档属性
| 名称 | 北师大版七年级下册数学《全等三角形》复习讲义 (3)(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 487.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-01 18:34:45 | ||
图片预览




文档简介
教学内容 全等三角形
教学目标 熟练掌握三角形的性质定理与判定定理
教学重点 如何证明三角形全等
教学难点 全等三角形的灵活运用
教学准备
教学过程
前课回顾
【知识梳理】 一、全等三角形
1.判定和性质
一般三角形
直角三角形
判定
边角边(SAS)、角边角(ASA)
角角边(AAS)、边边边(SSS)
具备一般三角形的判定方法
斜边和一条直角边对应相等(HL)
性质
对应边相等,对应角相等
对应中线相等,对应高相等,对应角平分线相等
注:① 判定两个三角形全等必须有一组边对应相等;
② 全等三角形面积相等.
2.证题的思路:
知识详解
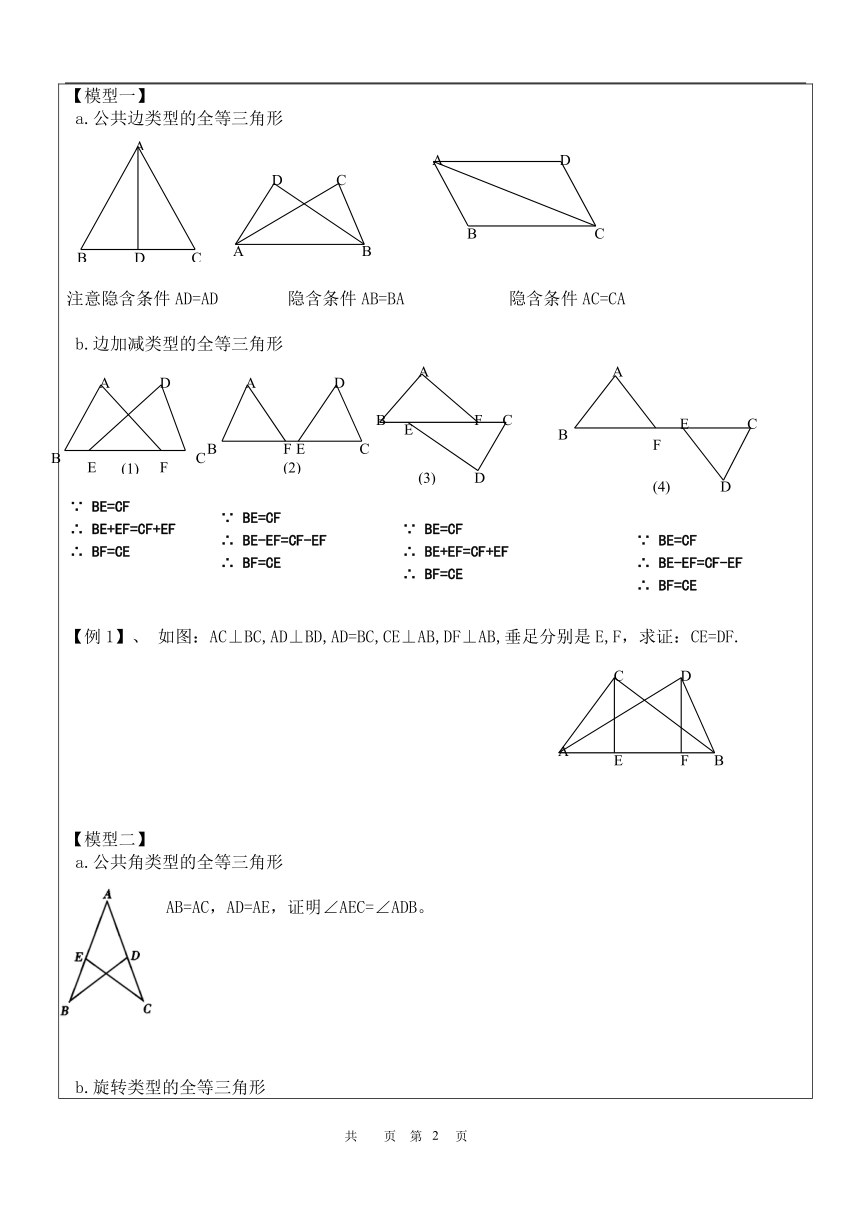
【模型一】 a.公共边类型的全等三角形
注意隐含条件AD=AD 隐含条件AB=BA 隐含条件AC=CA
b.边加减类型的全等三角形
【例1】、 如图:AC⊥BC,AD⊥BD,AD=BC,CE⊥AB,DF⊥AB,垂足分别是E,F,求证:CE=DF.
【模型二】
a.公共角类型的全等三角形
AB=AC,AD=AE,证明∠AEC=∠ADB。
b.旋转类型的全等三角形
【例2】、已知:如图(1),AB=AD,BC=DE,∠1=∠2.求证:(1)AC=AE; (2) ∠CAE=∠CDE.
【模型三】对顶角类型的全等三角形
图形1 图形2
【例3】、如图,AB∥DE,AB=DE,∠1=∠2.求证:BG=DF.
【模型四】等角或同角的余角相等
【例4】、已知,如图7, AD为△ABC的高, E为AC边上一点,BE交AD于F,且有BF=AC,FD=CD. 求证:(1)BE⊥AC;(2)若把条件BF=AC和结论BE⊥AC互换,那么这个命题成立吗?
变式训练
* 7、已知A、C、B共线,△ACD和△BCE为等边三角形,直线BD、AE交与F,AE、CD相较于点M, BD、AE相较于点N。如图1,
求证:AE=BD
求∠AFB的度数
求证:CM=CN
求证:MN∥AB
求证FC为∠AFB的平分线
求线段BF、EF、CF的关系
真题在线
巩固加深
随堂检测
1. 已知B,E,F,D在同一条直线上,AB=CD, ∠B=∠D,BF=DE.
求证:(1)AE=CF, (2) AE∥CF,(3) ∠AFE=∠CEF
2、(2011湖南衡阳,21,6分)如图,在△ABC中,AD是中线,分别过点B、C作AD及其延长线的垂线BE、CF,垂足分别为点E、F.求证:BE=CF.
3.如图,已知:,.求证:点B是线段AC的中点.
4.已知:∠1=∠2,CD=DE,EF//AB,求证:EF=AC
5.已知:AB=4,AC=2,D是BC中点,AD是整数,求AD
6.如图,在△ABC中,BD=DC,∠1=∠2,求证:AD⊥BC.
7.如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,A、B为垂足,AB交OM于点N.
求证:∠OAB=∠OBA
8.已知:如图所示,AB=AD,BC=DC,E、F分别是DC、BC的中点,求证: AE=AF。
9.已知:如图, ACBC于C , DEAC于E , ADAB于A , BC =AE.若AB = 5 ,求AD 的长?
10.(2011四川内江,18,9分)如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连结BE、EC.
试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
11. 如图,将两个一大、一小的等腰直角三角尺拼接 (A、B、D三点共线,AB=CB,EB=DB,
∠ABC=∠EBD=90°),连接AE、CD,试确定AE与CD的位置与数量关系,并证明你的结论.
12.如图所示:在△ABC和△DBC中,∠ACB=∠DBC=,E是BC的中点,EF⊥AB,垂足为F,且AB=DE.
(1)求证:BD=BC; (2)若BD=8cm,求AC的长.
教学总结
3
共 页 第 页
教学目标 熟练掌握三角形的性质定理与判定定理
教学重点 如何证明三角形全等
教学难点 全等三角形的灵活运用
教学准备
教学过程
前课回顾
【知识梳理】 一、全等三角形
1.判定和性质
一般三角形
直角三角形
判定
边角边(SAS)、角边角(ASA)
角角边(AAS)、边边边(SSS)
具备一般三角形的判定方法
斜边和一条直角边对应相等(HL)
性质
对应边相等,对应角相等
对应中线相等,对应高相等,对应角平分线相等
注:① 判定两个三角形全等必须有一组边对应相等;
② 全等三角形面积相等.
2.证题的思路:
知识详解
【模型一】 a.公共边类型的全等三角形
注意隐含条件AD=AD 隐含条件AB=BA 隐含条件AC=CA
b.边加减类型的全等三角形
【例1】、 如图:AC⊥BC,AD⊥BD,AD=BC,CE⊥AB,DF⊥AB,垂足分别是E,F,求证:CE=DF.
【模型二】
a.公共角类型的全等三角形
AB=AC,AD=AE,证明∠AEC=∠ADB。
b.旋转类型的全等三角形
【例2】、已知:如图(1),AB=AD,BC=DE,∠1=∠2.求证:(1)AC=AE; (2) ∠CAE=∠CDE.
【模型三】对顶角类型的全等三角形
图形1 图形2
【例3】、如图,AB∥DE,AB=DE,∠1=∠2.求证:BG=DF.
【模型四】等角或同角的余角相等
【例4】、已知,如图7, AD为△ABC的高, E为AC边上一点,BE交AD于F,且有BF=AC,FD=CD. 求证:(1)BE⊥AC;(2)若把条件BF=AC和结论BE⊥AC互换,那么这个命题成立吗?
变式训练
* 7、已知A、C、B共线,△ACD和△BCE为等边三角形,直线BD、AE交与F,AE、CD相较于点M, BD、AE相较于点N。如图1,
求证:AE=BD
求∠AFB的度数
求证:CM=CN
求证:MN∥AB
求证FC为∠AFB的平分线
求线段BF、EF、CF的关系
真题在线
巩固加深
随堂检测
1. 已知B,E,F,D在同一条直线上,AB=CD, ∠B=∠D,BF=DE.
求证:(1)AE=CF, (2) AE∥CF,(3) ∠AFE=∠CEF
2、(2011湖南衡阳,21,6分)如图,在△ABC中,AD是中线,分别过点B、C作AD及其延长线的垂线BE、CF,垂足分别为点E、F.求证:BE=CF.
3.如图,已知:,.求证:点B是线段AC的中点.
4.已知:∠1=∠2,CD=DE,EF//AB,求证:EF=AC
5.已知:AB=4,AC=2,D是BC中点,AD是整数,求AD
6.如图,在△ABC中,BD=DC,∠1=∠2,求证:AD⊥BC.
7.如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,A、B为垂足,AB交OM于点N.
求证:∠OAB=∠OBA
8.已知:如图所示,AB=AD,BC=DC,E、F分别是DC、BC的中点,求证: AE=AF。
9.已知:如图, ACBC于C , DEAC于E , ADAB于A , BC =AE.若AB = 5 ,求AD 的长?
10.(2011四川内江,18,9分)如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连结BE、EC.
试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
11. 如图,将两个一大、一小的等腰直角三角尺拼接 (A、B、D三点共线,AB=CB,EB=DB,
∠ABC=∠EBD=90°),连接AE、CD,试确定AE与CD的位置与数量关系,并证明你的结论.
12.如图所示:在△ABC和△DBC中,∠ACB=∠DBC=,E是BC的中点,EF⊥AB,垂足为F,且AB=DE.
(1)求证:BD=BC; (2)若BD=8cm,求AC的长.
教学总结
3
共 页 第 页
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
