北师大版七年级下册数学《全等三角形》复习讲义 (4)(无答案)
文档属性
| 名称 | 北师大版七年级下册数学《全等三角形》复习讲义 (4)(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 443.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-01 18:36:11 | ||
图片预览


文档简介
教学内容 全等三角形综合应用
教学目标 熟练掌握全等三角形的证明;常见辅助线的做法;利用全等三角形测距离等
教学重点 全等三角形的灵活应用
教学难点 全等三角形的灵活应用
教学准备
教学过程
前课回顾
全等三角形性质与判定
一般三角形
直角三角形
判定
边角边(SAS)、角边角(ASA)
角角边(AAS)、边边边(SSS)
具备一般三角形的判定方法
斜边和一条直角边对应相等(HL)
性质
对应边相等,对应角相等
对应中线相等,对应高相等,对应角平分线相等
注:① 判定两个三角形全等必须有一组边对应相等;
② 全等三角形面积相等
二、辅助线作法
1.等腰三角形的
2.有中点是
3.角平分线:
4.垂直平分线:① ;② ;③
5.证明和、差、倍、分等类型时用
6.做 ,构造全等三角形
7.特殊值法,有30度或60度时做
错题重现
1.如图,已知在△ABC中,∠B=60°,△ABC的角平分线AD,CE相交于点O,求证:(1)OE=OD;(2)DC+AE =AC
2.已知:如图(1),AB=AD,BC=DE,∠1=∠2.求证:(1)AC=AE; (2) ∠CAE=∠CDE.
知识详解
情境一 在一次战役中,我军阵地与敌军碉堡隔河相望,为了炸掉这个碉堡,需要知道碉堡与我军阵地距离,在不能过河测量又没有任何测量工具的情况下,一个战士想出来这样一个办法,他面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部,然后,他转过一个角度,保持刚才的姿势,这时视线落在了自己所在岸的某一点上,接着他用步测的办法量出自己与那个点的距离,这个距离就是他民碉堡间的距离。
解释战士采用的方法的数学道理。
情景二:
想一想
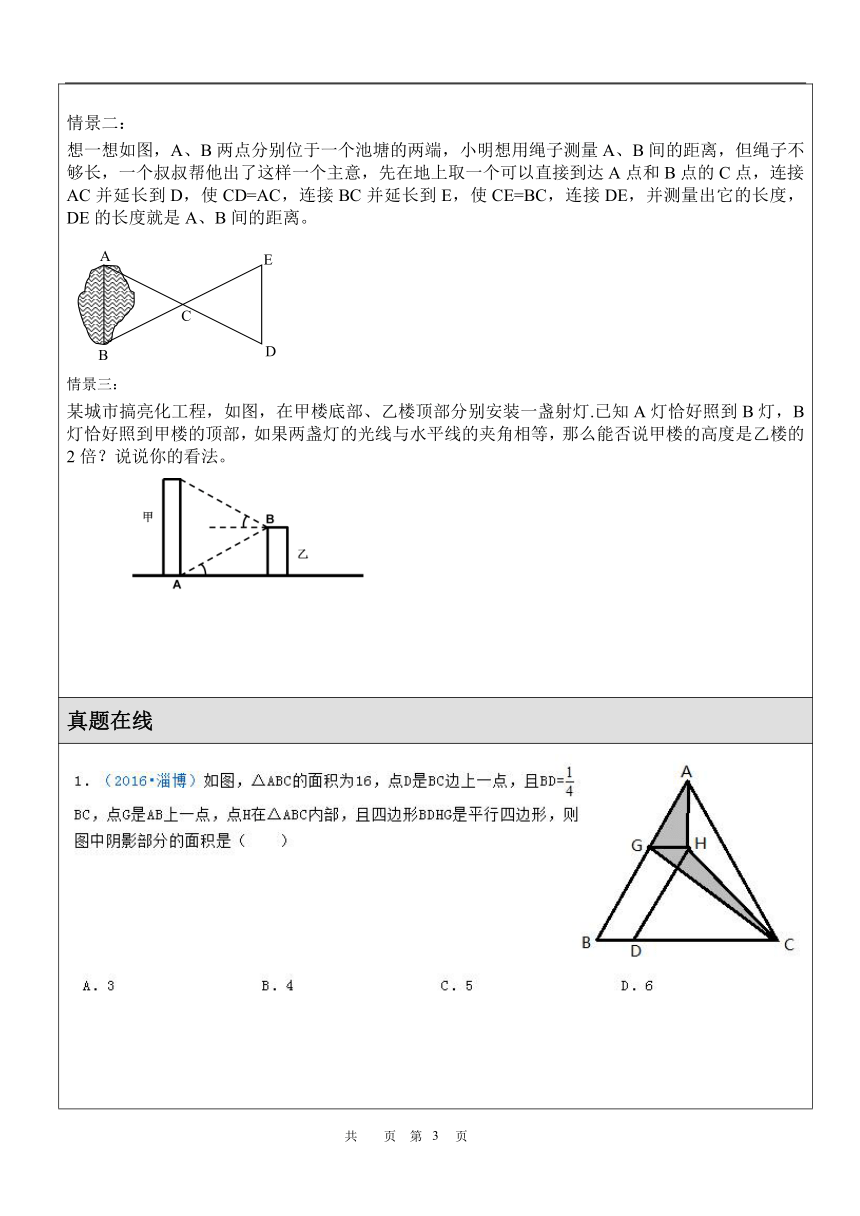
如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离,但绳子不够长,一个叔叔帮他出了这样一个主意,先在地上取一个可以直接到达A点和B点的C点,连接AC并延长到D,使CD=AC,连接BC并延长到E,使CE=BC,连接DE,并测量出它的长度,DE的长度就是A、B间的距离。
情景三:
某城市搞亮化工程,如图,在甲楼底部、乙楼顶部分别安装一盏射灯.已知A灯恰好照到B灯,B灯恰好照到甲楼的顶部,如果两盏灯的光线与水平线的夹角相等,那么能否说甲楼的高度是乙楼的2倍?说说你的看法。
真题在线
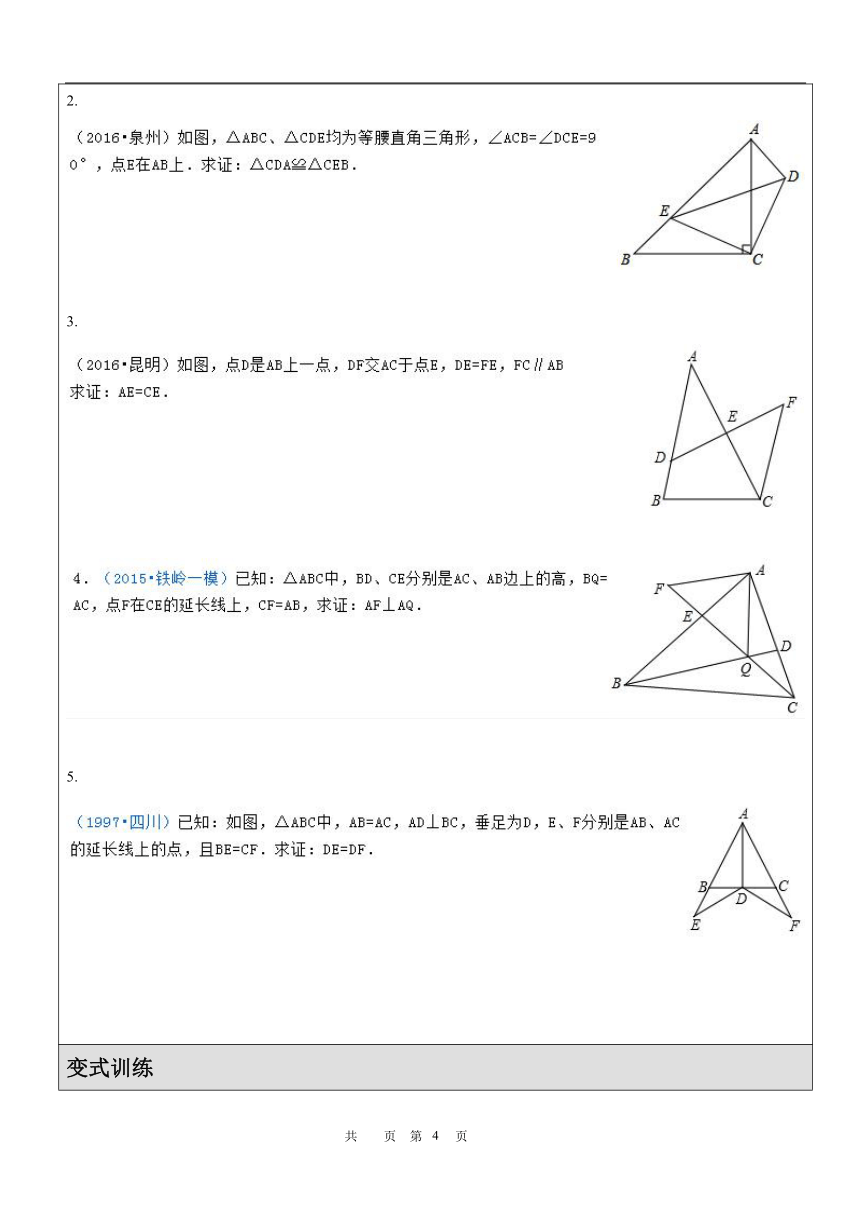
3.
5.
变式训练
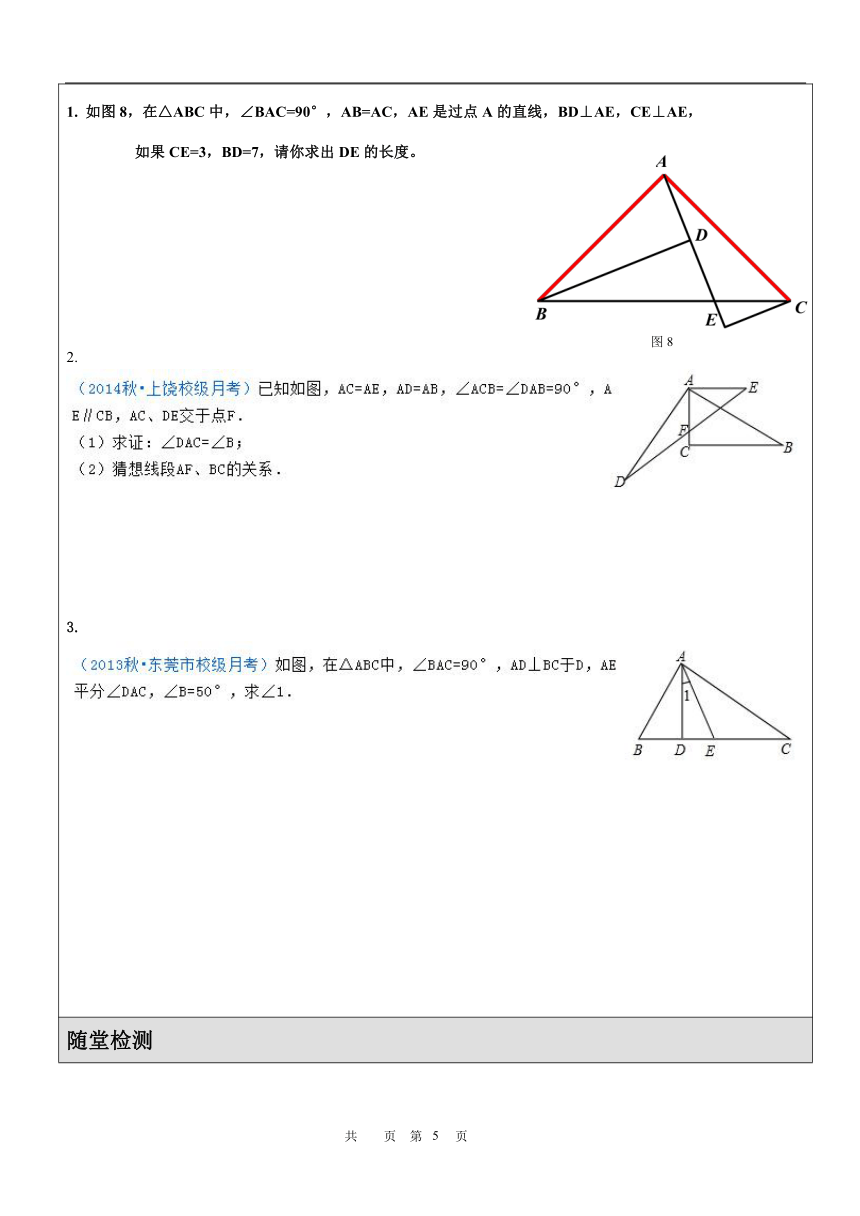
1. 如图8,在△ABC中,∠BAC=90°,AB=AC,AE是过点A的直线,BD⊥AE,CE⊥AE, 如果CE=3,BD=7,请你求出DE的长度。
2.
3.
随堂检测
1.
2.已知:交于点,且,求证:.
3.已知:.求证:.
4.
6. 如图,为等边三角形,点分别在上,且,与交于点。求的度数。
7. 如图,,,为上一点,,,交延长线于点。求证:。
8. 如图,已知OP平分∠AOB,C,D分别在OA、OB上,若∠PCO+∠PDO=180°,
求证:PC=PD.
9. 已知:如图,在正方形ABCD中,E为AD上一点,BF平分∠CBE交CD于F,求证:BE=CF+AE.
10.
12.
13. 已知:如图5—129,△ABC的∠B、∠C的平分线相交于点D,过D
作MN∥BC交AB、AC分别于点M、N,求证:BM+CN=MN
14. 已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE
15. P是∠BAC平分线AD上一点,AC>AB,求证:PC-PB16探索发现(共20分)
为在池塘两侧的A,B两处架桥,要想测量A,B两点的距离,有以下两种方法:
(1)如图所示,找一处看得见A,B的点P,连接AP并延长到D,使PA=PD,连接BP并延长到C,使PC=PB.测得CD=35m,就确定了AB也是35m,说明其中的理由;
(2)如图所示,也可先过B点作AB的垂线BF,再在BF上取C,D两点,使BC=CD.接着过点D作BD的垂线DE交AC的延线长于E,则测出DE的长即为A,B的距离.你认为这种方案是否切实可行,请说出你的理由.作BD⊥AB,ED⊥BF的目的是什么?若满足∠ABD=∠BDE≠90°,此方案是否仍然可行?为什么?
17 .已知:如图,DC∥AB,且DC=AE,E为AB的中点,
(1)求证:△AED≌△EBC.
(2)观看图前,在不添辅助线的情况下,除△EBC外,请再写出两个与△AED的面积相等的三角形.(直接写出结果,不要求证明):
3
共 页 第 页
教学目标 熟练掌握全等三角形的证明;常见辅助线的做法;利用全等三角形测距离等
教学重点 全等三角形的灵活应用
教学难点 全等三角形的灵活应用
教学准备
教学过程
前课回顾
全等三角形性质与判定
一般三角形
直角三角形
判定
边角边(SAS)、角边角(ASA)
角角边(AAS)、边边边(SSS)
具备一般三角形的判定方法
斜边和一条直角边对应相等(HL)
性质
对应边相等,对应角相等
对应中线相等,对应高相等,对应角平分线相等
注:① 判定两个三角形全等必须有一组边对应相等;
② 全等三角形面积相等
二、辅助线作法
1.等腰三角形的
2.有中点是
3.角平分线:
4.垂直平分线:① ;② ;③
5.证明和、差、倍、分等类型时用
6.做 ,构造全等三角形
7.特殊值法,有30度或60度时做
错题重现
1.如图,已知在△ABC中,∠B=60°,△ABC的角平分线AD,CE相交于点O,求证:(1)OE=OD;(2)DC+AE =AC
2.已知:如图(1),AB=AD,BC=DE,∠1=∠2.求证:(1)AC=AE; (2) ∠CAE=∠CDE.
知识详解
情境一 在一次战役中,我军阵地与敌军碉堡隔河相望,为了炸掉这个碉堡,需要知道碉堡与我军阵地距离,在不能过河测量又没有任何测量工具的情况下,一个战士想出来这样一个办法,他面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部,然后,他转过一个角度,保持刚才的姿势,这时视线落在了自己所在岸的某一点上,接着他用步测的办法量出自己与那个点的距离,这个距离就是他民碉堡间的距离。
解释战士采用的方法的数学道理。
情景二:
想一想
如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离,但绳子不够长,一个叔叔帮他出了这样一个主意,先在地上取一个可以直接到达A点和B点的C点,连接AC并延长到D,使CD=AC,连接BC并延长到E,使CE=BC,连接DE,并测量出它的长度,DE的长度就是A、B间的距离。
情景三:
某城市搞亮化工程,如图,在甲楼底部、乙楼顶部分别安装一盏射灯.已知A灯恰好照到B灯,B灯恰好照到甲楼的顶部,如果两盏灯的光线与水平线的夹角相等,那么能否说甲楼的高度是乙楼的2倍?说说你的看法。
真题在线
3.
5.
变式训练
1. 如图8,在△ABC中,∠BAC=90°,AB=AC,AE是过点A的直线,BD⊥AE,CE⊥AE, 如果CE=3,BD=7,请你求出DE的长度。
2.
3.
随堂检测
1.
2.已知:交于点,且,求证:.
3.已知:.求证:.
4.
6. 如图,为等边三角形,点分别在上,且,与交于点。求的度数。
7. 如图,,,为上一点,,,交延长线于点。求证:。
8. 如图,已知OP平分∠AOB,C,D分别在OA、OB上,若∠PCO+∠PDO=180°,
求证:PC=PD.
9. 已知:如图,在正方形ABCD中,E为AD上一点,BF平分∠CBE交CD于F,求证:BE=CF+AE.
10.
12.
13. 已知:如图5—129,△ABC的∠B、∠C的平分线相交于点D,过D
作MN∥BC交AB、AC分别于点M、N,求证:BM+CN=MN
14. 已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE
15. P是∠BAC平分线AD上一点,AC>AB,求证:PC-PB
为在池塘两侧的A,B两处架桥,要想测量A,B两点的距离,有以下两种方法:
(1)如图所示,找一处看得见A,B的点P,连接AP并延长到D,使PA=PD,连接BP并延长到C,使PC=PB.测得CD=35m,就确定了AB也是35m,说明其中的理由;
(2)如图所示,也可先过B点作AB的垂线BF,再在BF上取C,D两点,使BC=CD.接着过点D作BD的垂线DE交AC的延线长于E,则测出DE的长即为A,B的距离.你认为这种方案是否切实可行,请说出你的理由.作BD⊥AB,ED⊥BF的目的是什么?若满足∠ABD=∠BDE≠90°,此方案是否仍然可行?为什么?
17 .已知:如图,DC∥AB,且DC=AE,E为AB的中点,
(1)求证:△AED≌△EBC.
(2)观看图前,在不添辅助线的情况下,除△EBC外,请再写出两个与△AED的面积相等的三角形.(直接写出结果,不要求证明):
3
共 页 第 页
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
