北师大版七年级下册数学《全等三角形》全等三角形的判定(1)讲义(无答案)
文档属性
| 名称 | 北师大版七年级下册数学《全等三角形》全等三角形的判定(1)讲义(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 153.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-01 18:23:39 | ||
图片预览

文档简介
12.2全等三角形的判定(1)
知识点一:全等三角形的判定
1、全等三角形的判定一:三边对应相等的两个三角形全等,简_???_为“边边边”或“SSS”.
用数学语言表述:在△ABC和中,
∵ ∴△ABC≌(SSS)
2、这个判定方法告诉我们:当三角形的三边都确定后,其形状、大小都随之确定,这就是三角形的稳定性.
3、全等三角形的判定二:两边和他们的夹角对应相等的两个三角形全等,简_???_为“边角边”或“SAS”.
用数学语言表述:在△ABC和中,
∵ ∴△ABC≌(SAS)
知识点二:全等三角形的性质
全等三角形的对应边相等;全等三角形的对应角相等,全等三角形的周长、面积相等.
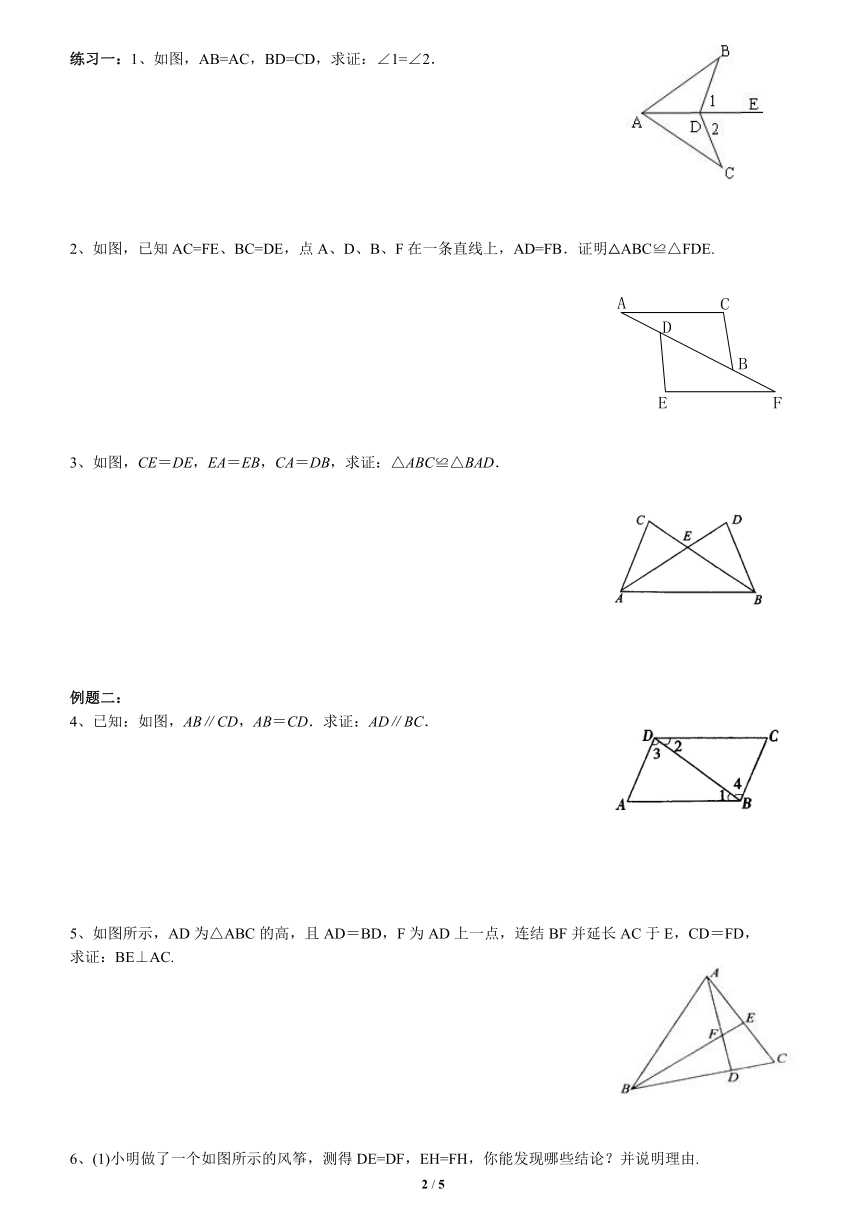
例题一:1、已知:如图,AB=DE,AC=DF,BE=CF.求证:∠A=∠D.
2、如图,已知AB=CD,AC=BD,求证:∠A=∠D.
3、如图,AD=CB,E、F是AC上两动点,且有DE=BF.
(1)若E、F运动至如图①所示的位置,且有AF=CE,求证:△ADE≌△CBF.
(2)若E、F运动至如图②所示的位置,仍有AF=CE,那么△ADE≌△CBF还成立吗?为什么?
(3)若E、F不重合,AD和CB平行吗?说明理由.
练习一:1、如图,AB=AC,BD=CD,求证:∠1=∠2.
2、如图,已知AC=FE、BC=DE,点A、D、B、F在一条直线上,AD=FB.证明△ABC≌△FDE.
3、如图,CE=DE,EA=EB,CA=DB,求证:△ABC≌△BAD.
例题二:
4、已知:如图,AB∥CD,AB=CD.求证:AD∥BC.
5、如图所示,AD为△ABC的高,且AD=BD,F为AD上一点,连结BF并延长AC于E,CD=FD,
求证:BE⊥AC.
6、(1)小明做了一个如图所示的风筝,测得DE=DF,EH=FH,你能发现哪些结论?并说明理由.
(2)如图,∠1=∠2,AB=AD,AE=AC,求证BC=DE.
练习二:
4、已知:如图,AB=AC,BE=CD.求证:∠B=∠C.
5、已知:如图,AB=AD,AC=AE,∠1=∠2.求证:BC=DE.
6、已知:如图,AC⊥BD,BC=CE,AC=DC,求证:∠B+∠D=90°.
第二部分:能力拓展
例题:7、如图,在△ABC中,AB=AC,D是BC的中点,点E在AD上,找出图中全等的三角形,并说明理由.
8、如图,已知CA=CB,AD=BD,M、N分别是CA、CB的中点,求证:DM=DN.
跟进练习:7、已知,如图A、F、C、D四点在一直线上,AF= CD,AB∥DE,且AB= DE,求证:(1)△ABC≌△DEF;(2)CBF=FEC.
8、AB=AC,DB=DC,F是AD的延长线上的一点。求证:BF=CF.
课 后 作 业
1、如图,AB=AC,AD = AE,CD=BE.求证:∠DAB=∠EAC.
2、如图, A,C,D,B在同一条直线上,AE=BF,AD=BC,AE∥BF.求证:FD∥EC.
3、如图,AB=AC,AD=AE,AB⊥AC,AD⊥AE,问BD和CE相等吗?为什么?
4、如图,△ABC≌△EDC,求证:BE=AD.
5、已知:如图所示,AB=AD,BC=DC,E、F分别是DC、BC的中点,求证:AE=AF.
1 / 6
知识点一:全等三角形的判定
1、全等三角形的判定一:三边对应相等的两个三角形全等,简_???_为“边边边”或“SSS”.
用数学语言表述:在△ABC和中,
∵ ∴△ABC≌(SSS)
2、这个判定方法告诉我们:当三角形的三边都确定后,其形状、大小都随之确定,这就是三角形的稳定性.
3、全等三角形的判定二:两边和他们的夹角对应相等的两个三角形全等,简_???_为“边角边”或“SAS”.
用数学语言表述:在△ABC和中,
∵ ∴△ABC≌(SAS)
知识点二:全等三角形的性质
全等三角形的对应边相等;全等三角形的对应角相等,全等三角形的周长、面积相等.
例题一:1、已知:如图,AB=DE,AC=DF,BE=CF.求证:∠A=∠D.
2、如图,已知AB=CD,AC=BD,求证:∠A=∠D.
3、如图,AD=CB,E、F是AC上两动点,且有DE=BF.
(1)若E、F运动至如图①所示的位置,且有AF=CE,求证:△ADE≌△CBF.
(2)若E、F运动至如图②所示的位置,仍有AF=CE,那么△ADE≌△CBF还成立吗?为什么?
(3)若E、F不重合,AD和CB平行吗?说明理由.
练习一:1、如图,AB=AC,BD=CD,求证:∠1=∠2.
2、如图,已知AC=FE、BC=DE,点A、D、B、F在一条直线上,AD=FB.证明△ABC≌△FDE.
3、如图,CE=DE,EA=EB,CA=DB,求证:△ABC≌△BAD.
例题二:
4、已知:如图,AB∥CD,AB=CD.求证:AD∥BC.
5、如图所示,AD为△ABC的高,且AD=BD,F为AD上一点,连结BF并延长AC于E,CD=FD,
求证:BE⊥AC.
6、(1)小明做了一个如图所示的风筝,测得DE=DF,EH=FH,你能发现哪些结论?并说明理由.
(2)如图,∠1=∠2,AB=AD,AE=AC,求证BC=DE.
练习二:
4、已知:如图,AB=AC,BE=CD.求证:∠B=∠C.
5、已知:如图,AB=AD,AC=AE,∠1=∠2.求证:BC=DE.
6、已知:如图,AC⊥BD,BC=CE,AC=DC,求证:∠B+∠D=90°.
第二部分:能力拓展
例题:7、如图,在△ABC中,AB=AC,D是BC的中点,点E在AD上,找出图中全等的三角形,并说明理由.
8、如图,已知CA=CB,AD=BD,M、N分别是CA、CB的中点,求证:DM=DN.
跟进练习:7、已知,如图A、F、C、D四点在一直线上,AF= CD,AB∥DE,且AB= DE,求证:(1)△ABC≌△DEF;(2)CBF=FEC.
8、AB=AC,DB=DC,F是AD的延长线上的一点。求证:BF=CF.
课 后 作 业
1、如图,AB=AC,AD = AE,CD=BE.求证:∠DAB=∠EAC.
2、如图, A,C,D,B在同一条直线上,AE=BF,AD=BC,AE∥BF.求证:FD∥EC.
3、如图,AB=AC,AD=AE,AB⊥AC,AD⊥AE,问BD和CE相等吗?为什么?
4、如图,△ABC≌△EDC,求证:BE=AD.
5、已知:如图所示,AB=AD,BC=DC,E、F分别是DC、BC的中点,求证:AE=AF.
1 / 6
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
