2020-2021年 高中数学人教B版必修四 1.3.2余弦函数图象与性质1(共14张PPT)
文档属性
| 名称 | 2020-2021年 高中数学人教B版必修四 1.3.2余弦函数图象与性质1(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
1.3.2
余弦函数的图象与性质
高中数学B版必修四
回忆:
的图象是如何得到的?
正弦函数
借助于单位圆中的正弦函数线得到对应的图象
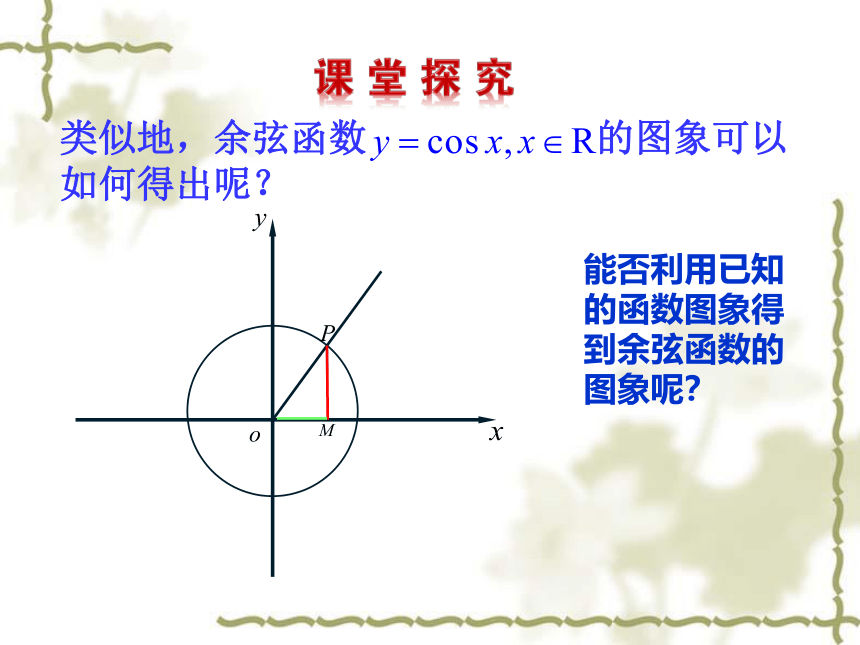
类似地,余弦函数
的图象可以如何得出呢?
能否利用已知的函数图象得到余弦函数的图象呢?
思考:如何将余弦函数用诱导公式写成正弦函数?
注:余弦曲线的图象可以通过将正弦曲线向左平移
个单位长度而得到,余弦函数的图象叫作余弦曲线。
根据诱导公式,可得:
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
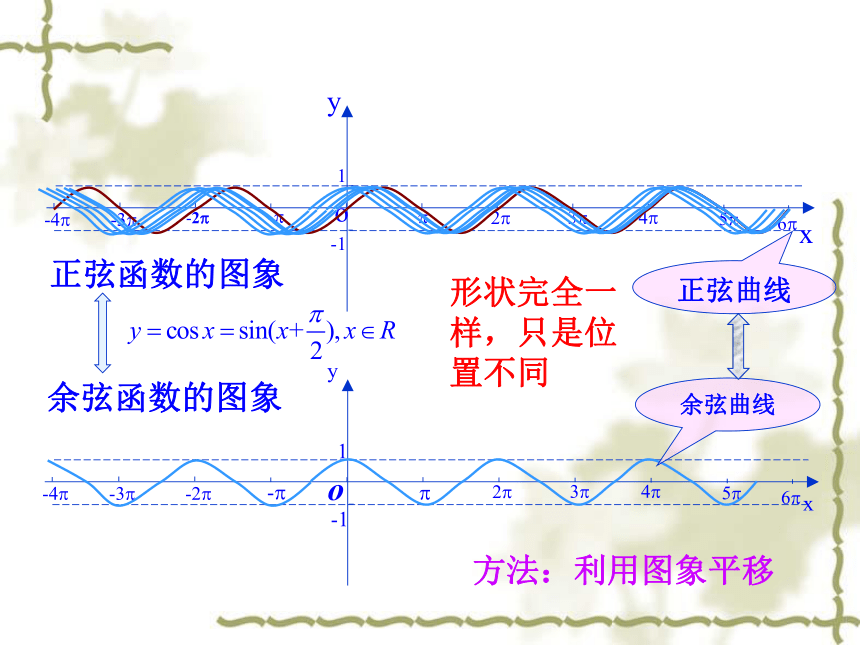
余弦函数的图象
正弦函数的图象
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
余弦曲线
正弦曲线
形状完全一样,只是位置不同
方法:利用图象平移
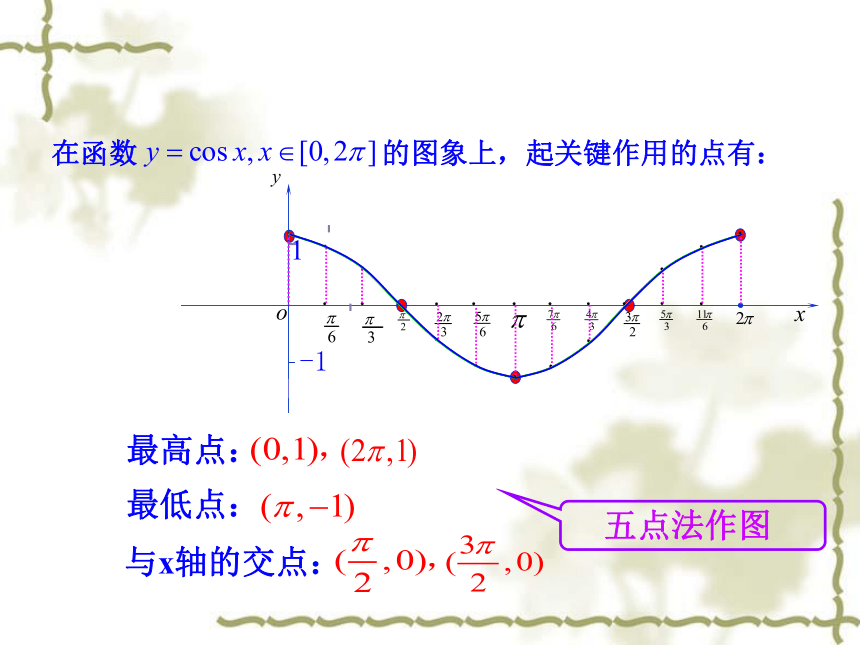
最高点:
最低点:
与x轴的交点:
在函数
的图象上,起关键作用的点有:
五点法作图
-1
-
-
-
1
-
正弦函数
的性质
1、定义域
2、值域
3、最值
4、奇偶性
5、周期性
6、单调性
7、对称性
余弦曲线:
思考1:观察图中所示的余弦曲线,说出值域,并说明当
取何值时,函数取得最值。
值域:[-1,1]
探究点2
余弦函数的性质
例1
求下列函数的最大值和最小值。
解:
的最大值为4,最小值为-2;
的最大值为3,最小值为1。
取何值时,函数取得最值?
奇偶性:关于y轴对称,偶函数
思考2:观察图中所示的余弦曲线,说出它们的图象的对称性?
提示:由图象可以看出,关于y轴对称.
余弦曲线:
思考2:如何判断三角函数的奇偶性?
提示:(1)利用图象法:若图象关于原点对称,则函数为奇函数;若图象关于y轴对称,则函数为偶函数.
(2)根据奇偶性的定义判断:若对定义域内的任意x都有f(-x)=f(x),则函数为偶函数;若对定义域内的任意x都有f(-x)=-f(x),则函数为奇函数.
例2
判断函数的奇偶性:
通过本节学习应掌握以下几点:
P61
习题1-3A
3
(1)、(3),
6(3)
P69
巩固与提高
14(1)
1.3.2
余弦函数的图象与性质
高中数学B版必修四
回忆:
的图象是如何得到的?
正弦函数
借助于单位圆中的正弦函数线得到对应的图象
类似地,余弦函数
的图象可以如何得出呢?
能否利用已知的函数图象得到余弦函数的图象呢?
思考:如何将余弦函数用诱导公式写成正弦函数?
注:余弦曲线的图象可以通过将正弦曲线向左平移
个单位长度而得到,余弦函数的图象叫作余弦曲线。
根据诱导公式,可得:
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
余弦函数的图象
正弦函数的图象
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
余弦曲线
正弦曲线
形状完全一样,只是位置不同
方法:利用图象平移
最高点:
最低点:
与x轴的交点:
在函数
的图象上,起关键作用的点有:
五点法作图
-1
-
-
-
1
-
正弦函数
的性质
1、定义域
2、值域
3、最值
4、奇偶性
5、周期性
6、单调性
7、对称性
余弦曲线:
思考1:观察图中所示的余弦曲线,说出值域,并说明当
取何值时,函数取得最值。
值域:[-1,1]
探究点2
余弦函数的性质
例1
求下列函数的最大值和最小值。
解:
的最大值为4,最小值为-2;
的最大值为3,最小值为1。
取何值时,函数取得最值?
奇偶性:关于y轴对称,偶函数
思考2:观察图中所示的余弦曲线,说出它们的图象的对称性?
提示:由图象可以看出,关于y轴对称.
余弦曲线:
思考2:如何判断三角函数的奇偶性?
提示:(1)利用图象法:若图象关于原点对称,则函数为奇函数;若图象关于y轴对称,则函数为偶函数.
(2)根据奇偶性的定义判断:若对定义域内的任意x都有f(-x)=f(x),则函数为偶函数;若对定义域内的任意x都有f(-x)=-f(x),则函数为奇函数.
例2
判断函数的奇偶性:
通过本节学习应掌握以下几点:
P61
习题1-3A
3
(1)、(3),
6(3)
P69
巩固与提高
14(1)
