2020-2021年 高一数学人教B版必修四 1.3.2余弦函数图象与性质(共16张PPT)
文档属性
| 名称 | 2020-2021年 高一数学人教B版必修四 1.3.2余弦函数图象与性质(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 815.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 16:40:56 | ||
图片预览



文档简介
(共16张PPT)
余弦函数图象与性质
高一数学组
y
x
o
1
-1
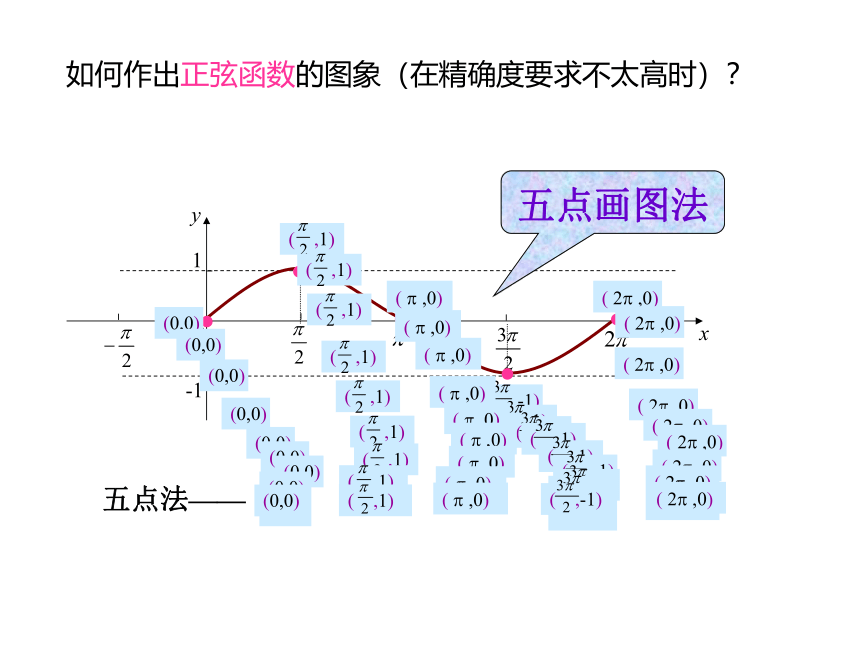
如何作出正弦函数的图象(在精确度要求不太高时)?
(0,0)
(
,1)
(
?
,0)
(
,-1)
(
2?
,0)
五点画图法
五点法——
(0,0)
(
,1)
(
?
,0)
(
,1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,-1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,-1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,-1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,-1)
(
2?
,0)
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
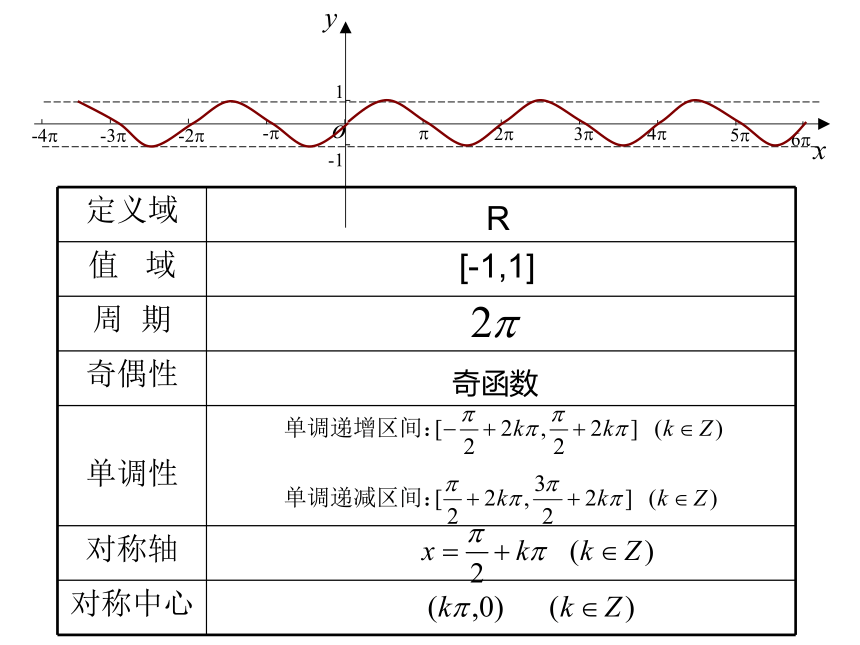
定义域
值
域
周
期
奇偶性
单调性
对称轴
对称中心
R
[-1,1]
奇函数
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
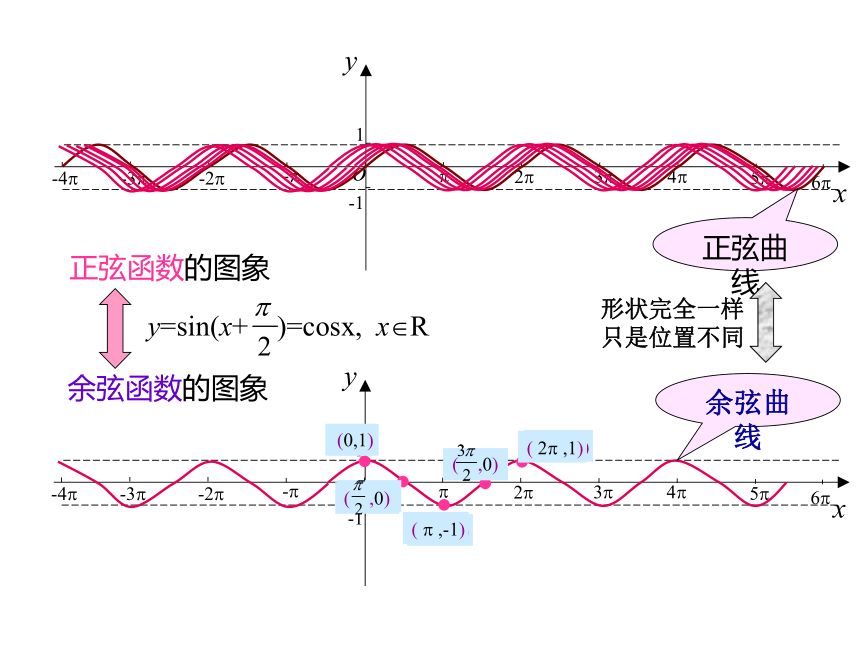
余弦函数的图象
正弦函数的图象
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y=sin(x+
)=cosx,
x?R
余弦曲线
(0,1)
(
,0)
(
?
,-1)
(
,0)
(
2?
,1)
正弦曲线
形状完全一样只是位置不同
(0,1)
(
,0)
(
?
,-1)
(
,0)
(
2?
,1)
-
-
1
-1
-
-
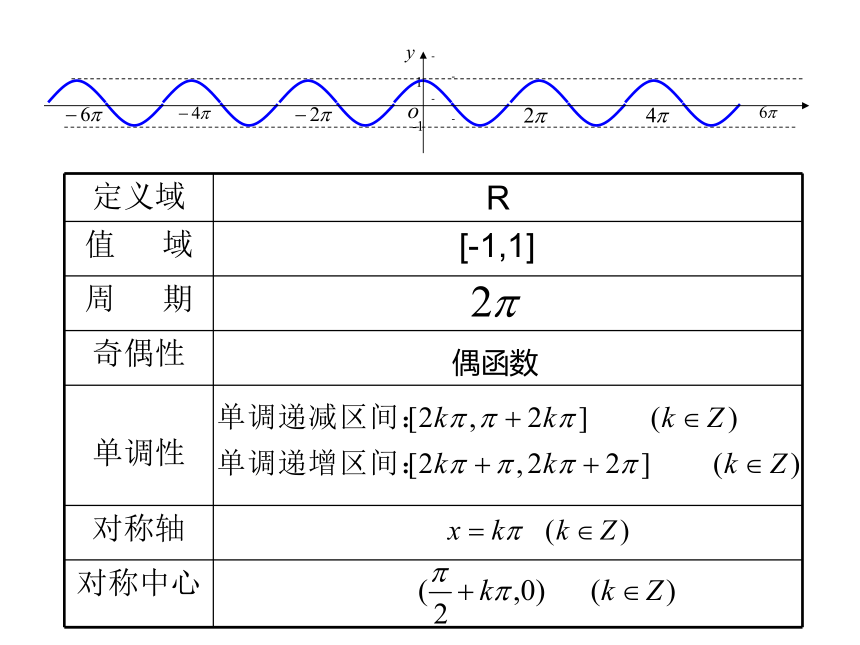
定义域
值
域
周
期
奇偶性
单调性
对称轴
对称中心
R
[-1,1]
偶函数
例1、求下列函数的最大值和最小值:
解(1)
小结:(1)明确最值的取得点
(2)牢记余弦函数的值域
例2、判断下列函数的奇偶性:
(1)
y=cosx+2
(2)
y=sinx·cosx
小结:
练习:比较大小
定义域
值
域
周
期
奇偶性
单调性
对称轴
对称中心
R
[-1,1]
偶函数
小结:1、知识要点
2、题型方法:求周期。最值。单调区间
比较大小
3、数学思想:数形结合
类比推理
作业:课本
选做题:已知函数
(1)求
的单调增区间;
(2)当
时,
的最大值为4,求
的值;
(3)在(2)的条件下,请说明如何由函数
的图象变换得到
的图象。
余弦函数图象与性质
高一数学组
y
x
o
1
-1
如何作出正弦函数的图象(在精确度要求不太高时)?
(0,0)
(
,1)
(
?
,0)
(
,-1)
(
2?
,0)
五点画图法
五点法——
(0,0)
(
,1)
(
?
,0)
(
,1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,-1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,-1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,-1)
(
2?
,0)
(0,0)
(
,1)
(
?
,0)
(
,-1)
(
2?
,0)
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
定义域
值
域
周
期
奇偶性
单调性
对称轴
对称中心
R
[-1,1]
奇函数
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
余弦函数的图象
正弦函数的图象
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y=sin(x+
)=cosx,
x?R
余弦曲线
(0,1)
(
,0)
(
?
,-1)
(
,0)
(
2?
,1)
正弦曲线
形状完全一样只是位置不同
(0,1)
(
,0)
(
?
,-1)
(
,0)
(
2?
,1)
-
-
1
-1
-
-
定义域
值
域
周
期
奇偶性
单调性
对称轴
对称中心
R
[-1,1]
偶函数
例1、求下列函数的最大值和最小值:
解(1)
小结:(1)明确最值的取得点
(2)牢记余弦函数的值域
例2、判断下列函数的奇偶性:
(1)
y=cosx+2
(2)
y=sinx·cosx
小结:
练习:比较大小
定义域
值
域
周
期
奇偶性
单调性
对称轴
对称中心
R
[-1,1]
偶函数
小结:1、知识要点
2、题型方法:求周期。最值。单调区间
比较大小
3、数学思想:数形结合
类比推理
作业:课本
选做题:已知函数
(1)求
的单调增区间;
(2)当
时,
的最大值为4,求
的值;
(3)在(2)的条件下,请说明如何由函数
的图象变换得到
的图象。
