圆的对称性(二)
图片预览



文档简介
(共18张PPT)
垂径定理
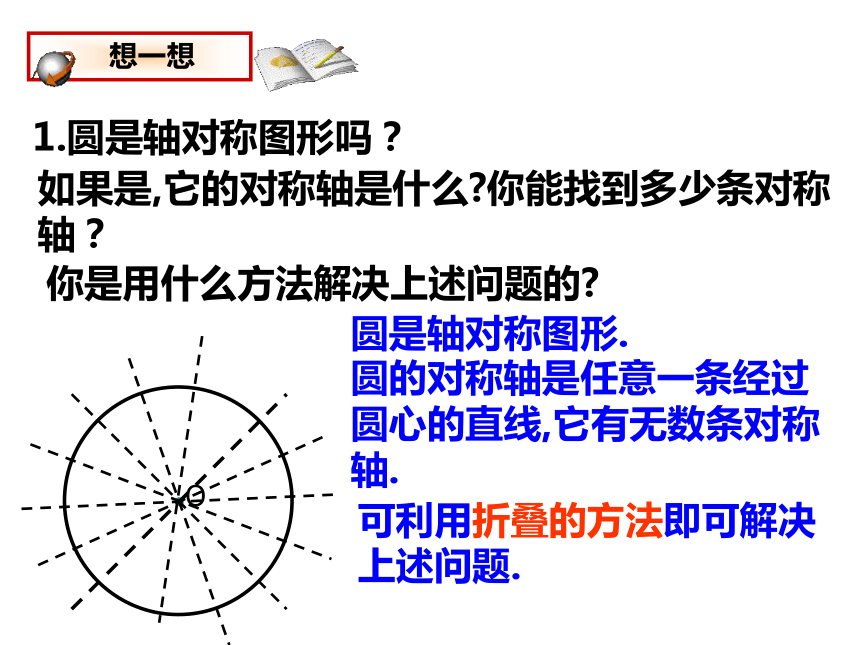
圆是轴对称图形.
想一想
圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.
●O
可利用折叠的方法即可解决上述问题.
1.圆是轴对称图形吗?
如果是,它的对称轴是什么 你能找到多少条对称轴?
你是用什么方法解决上述问题的
AM=BM,
垂径定理
如图:AB是⊙O的一条弦.
(2)你能发现图中有哪些等量关系 与同伴说说你的想法.
探究活动1
作直径CD,使CD⊥AB,垂足为M.
●O
(1)所作的图是轴对称图形吗 如果是,其对称轴是什么
发现图中有:
A
B
C
D
M└
CD是直径
CD⊥AB
可推得
⌒
⌒
AC=BC,
⌒
⌒
AD=BD.
操作探究
垂径定理
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
题设
结论
(1)过圆心
(2)垂直于弦
}
{
(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧
知二得三
动动脑筋
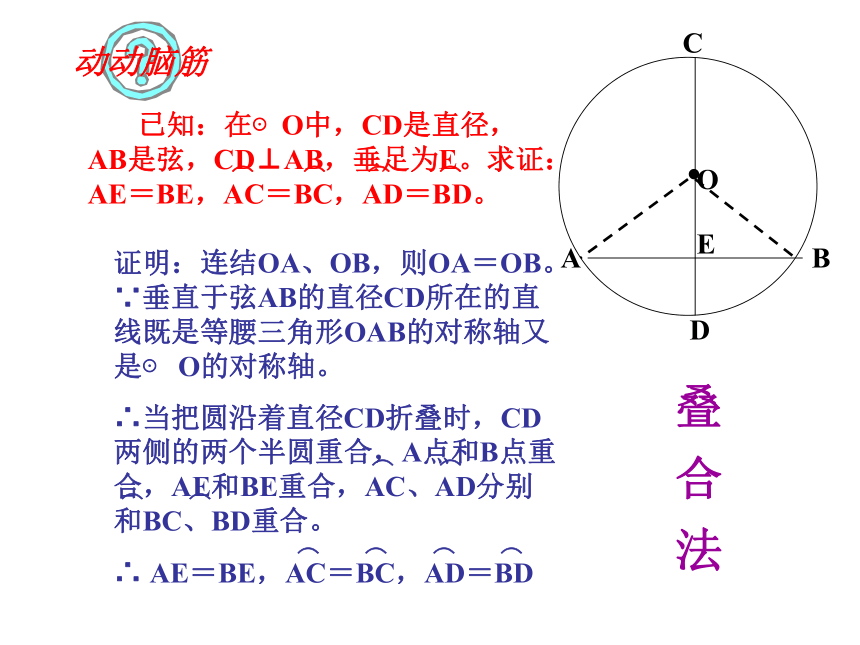
已知:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E。求证:AE=BE,AC=BC,AD=BD。
⌒
⌒
⌒
⌒
C
.
O
A
E
B
D
叠 合 法
证明:连结OA、OB,则OA=OB。 ∵垂直于弦AB的直径CD所在的直线既是等腰三角形OAB的对称轴又是⊙ O的对称轴。
∴当把圆沿着直径CD折叠时,CD两侧的两个半圆重合,A点和B点重合,AE和BE重合,AC、AD分别和BC、BD重合。
∴ AE=BE,AC=BC,AD=BD
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
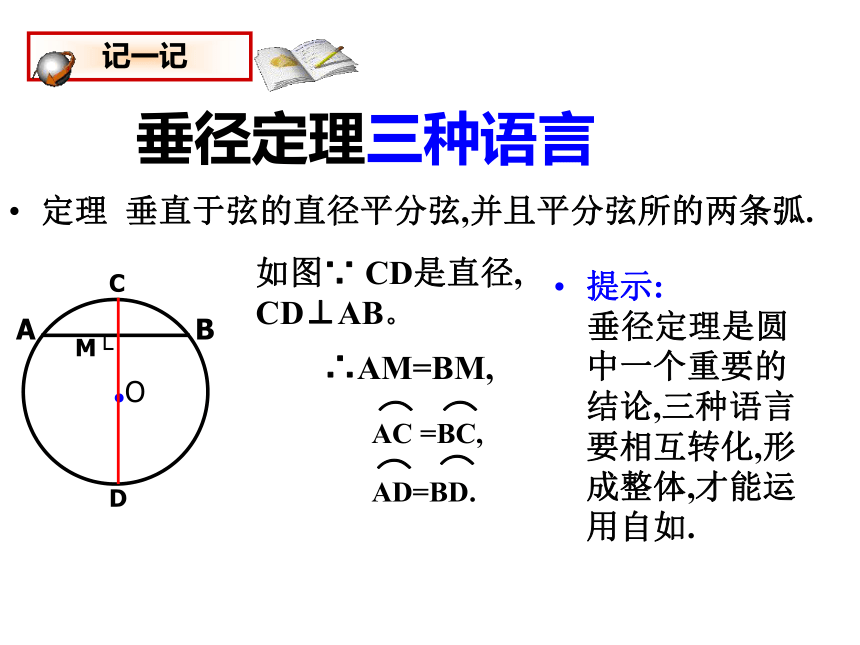
垂径定理三种语言
定理 垂直于弦的直径平分弦,并且平分弦所的两条弧.
提示:
垂径定理是圆中一个重要的结论,三种语言要相互转化,形成整体,才能运用自如.
记一记
●O
A
B
C
D
M└
如图∵ CD是直径, CD⊥AB。
∴AM=BM,
⌒
⌒
AC =BC,
⌒
⌒
AD=BD.
CD⊥AB,
垂径定理的推论
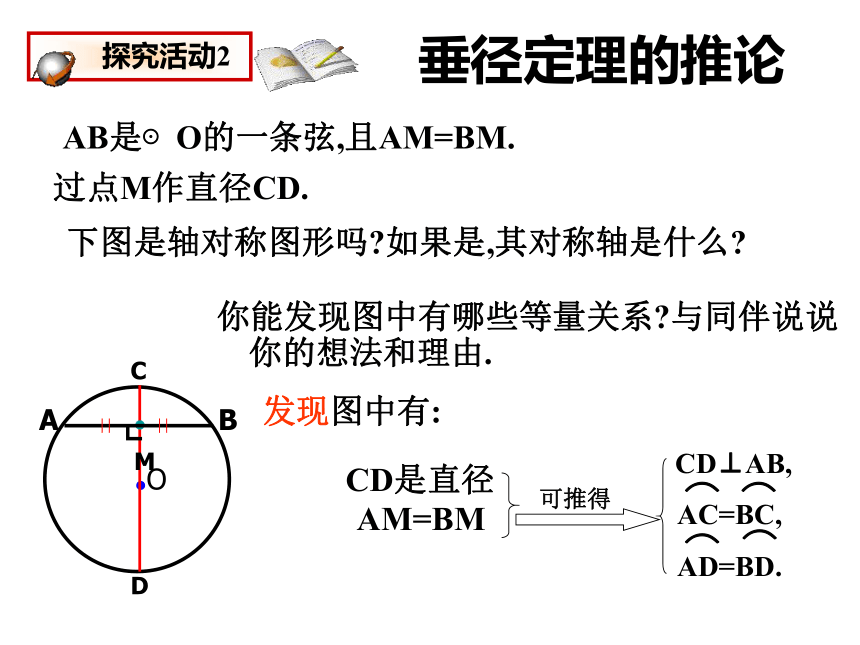
AB是⊙O的一条弦,且AM=BM.
你能发现图中有哪些等量关系 与同伴说说你的想法和理由.
探究活动2
过点M作直径CD.
●O
下图是轴对称图形吗 如果是,其对称轴是什么
发现图中有:
C
D
CD是直径
AM=BM
可推得
⌒
⌒
AC=BC,
⌒
⌒
AD=BD.
●
M
A
B
┗
垂径定理的推论:
(1)推论1
① 平分弦(不是直径)的直径垂直与弦并且平分弦所对的两条弧。
②弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
③平分弦所对的一条弧的直径垂直平分弦,并且平分弦所对的另一条弧。
如果圆的两条弦互相平行,那么这两条弦所夹的弧相等吗
提示: 这两条弦在圆中位置有两种情况:
垂径定理的推论
●O
A
B
C
D
1.两条弦在圆心的同侧
●O
A
B
C
D
2.两条弦在圆心的两侧
推论2:圆的两条平行弦所夹的弧相等.
练一练
驶向胜利的彼岸
挑战自我
1、判断:
⑴垂直于弦的直线平分这条弦,并且平分弦所对的两条弧. ( )
⑵平分弦所对的一条弧的直径一定平分这条弦所对的另一条弧. ( )
⑶经过弦的中点的直径一定垂直于弦.( )
⑷圆的两条弦所夹的弧相等,则这两条弦平行. ( )
⑸弦的垂直平分线一定平分这条弦所对的弧. ( )
√
√
3.已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。你认为AC和BD有什么关系?为什么?
证明:相等。理由:
过O作OE⊥AB,垂足为E,
∴AE=BE,CE=DE。
∴ AE-CE=BE-DE
∴AC=BD
.
A
C
D
B
O
E
2.在半径为5㎜的⊙O中,弦AB=8㎜,则O到AB的距离= ,∠OAB的余弦值= 。
O
A
B
P
0.8
3mm
注意:解决有关弦的问题,过圆心作弦的垂线,是一种常用的辅助线添法.
C
D
A
B
E
4.平分已知弧AB
已知:AB
作法:
⒈ 连结AB.
⒉作AB的垂直平分线 CD,交弧AB于点E.
点E就是所求弧AB的中点。
求作:AB的中点
⌒
⌒
你能破镜重圆吗?
A
B
A
C
m
n
·
O
1.作弦AB.AC及它们的垂直平分线m.n,交于O点;
2.以O为圆心,OA为半径作圆。
你能破镜重圆吗?
A
B
A
C
m
n
·
O
1.作弦AB.AC及它们的垂直平分线m.n,交于O点;
2.以O为圆心,OA为半径作圆。
课堂总结
回顾与思考
1.圆的基本性质:(1)圆的中心对称性(2)圆的轴对称性(3)圆的旋转不变性
4.垂径定理及推论的应用:(1)计算(2)证明(3)作图
2.垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧
3.垂径定理的推论:
(1)推论1① 平分弦(不是直径)的直径垂直与弦并且平分弦所对的两条弧。
②弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
③平分弦所对的一条弧的直径垂直平分弦,并且平分弦所对的另一条弧。
(2)推论2:圆内的两条平行弦所夹的弧相等。
作业:
教材
3.4.5
再 见
谢谢大家
垂径定理
圆是轴对称图形.
想一想
圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.
●O
可利用折叠的方法即可解决上述问题.
1.圆是轴对称图形吗?
如果是,它的对称轴是什么 你能找到多少条对称轴?
你是用什么方法解决上述问题的
AM=BM,
垂径定理
如图:AB是⊙O的一条弦.
(2)你能发现图中有哪些等量关系 与同伴说说你的想法.
探究活动1
作直径CD,使CD⊥AB,垂足为M.
●O
(1)所作的图是轴对称图形吗 如果是,其对称轴是什么
发现图中有:
A
B
C
D
M└
CD是直径
CD⊥AB
可推得
⌒
⌒
AC=BC,
⌒
⌒
AD=BD.
操作探究
垂径定理
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
题设
结论
(1)过圆心
(2)垂直于弦
}
{
(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧
知二得三
动动脑筋
已知:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E。求证:AE=BE,AC=BC,AD=BD。
⌒
⌒
⌒
⌒
C
.
O
A
E
B
D
叠 合 法
证明:连结OA、OB,则OA=OB。 ∵垂直于弦AB的直径CD所在的直线既是等腰三角形OAB的对称轴又是⊙ O的对称轴。
∴当把圆沿着直径CD折叠时,CD两侧的两个半圆重合,A点和B点重合,AE和BE重合,AC、AD分别和BC、BD重合。
∴ AE=BE,AC=BC,AD=BD
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
垂径定理三种语言
定理 垂直于弦的直径平分弦,并且平分弦所的两条弧.
提示:
垂径定理是圆中一个重要的结论,三种语言要相互转化,形成整体,才能运用自如.
记一记
●O
A
B
C
D
M└
如图∵ CD是直径, CD⊥AB。
∴AM=BM,
⌒
⌒
AC =BC,
⌒
⌒
AD=BD.
CD⊥AB,
垂径定理的推论
AB是⊙O的一条弦,且AM=BM.
你能发现图中有哪些等量关系 与同伴说说你的想法和理由.
探究活动2
过点M作直径CD.
●O
下图是轴对称图形吗 如果是,其对称轴是什么
发现图中有:
C
D
CD是直径
AM=BM
可推得
⌒
⌒
AC=BC,
⌒
⌒
AD=BD.
●
M
A
B
┗
垂径定理的推论:
(1)推论1
① 平分弦(不是直径)的直径垂直与弦并且平分弦所对的两条弧。
②弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
③平分弦所对的一条弧的直径垂直平分弦,并且平分弦所对的另一条弧。
如果圆的两条弦互相平行,那么这两条弦所夹的弧相等吗
提示: 这两条弦在圆中位置有两种情况:
垂径定理的推论
●O
A
B
C
D
1.两条弦在圆心的同侧
●O
A
B
C
D
2.两条弦在圆心的两侧
推论2:圆的两条平行弦所夹的弧相等.
练一练
驶向胜利的彼岸
挑战自我
1、判断:
⑴垂直于弦的直线平分这条弦,并且平分弦所对的两条弧. ( )
⑵平分弦所对的一条弧的直径一定平分这条弦所对的另一条弧. ( )
⑶经过弦的中点的直径一定垂直于弦.( )
⑷圆的两条弦所夹的弧相等,则这两条弦平行. ( )
⑸弦的垂直平分线一定平分这条弦所对的弧. ( )
√
√
3.已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。你认为AC和BD有什么关系?为什么?
证明:相等。理由:
过O作OE⊥AB,垂足为E,
∴AE=BE,CE=DE。
∴ AE-CE=BE-DE
∴AC=BD
.
A
C
D
B
O
E
2.在半径为5㎜的⊙O中,弦AB=8㎜,则O到AB的距离= ,∠OAB的余弦值= 。
O
A
B
P
0.8
3mm
注意:解决有关弦的问题,过圆心作弦的垂线,是一种常用的辅助线添法.
C
D
A
B
E
4.平分已知弧AB
已知:AB
作法:
⒈ 连结AB.
⒉作AB的垂直平分线 CD,交弧AB于点E.
点E就是所求弧AB的中点。
求作:AB的中点
⌒
⌒
你能破镜重圆吗?
A
B
A
C
m
n
·
O
1.作弦AB.AC及它们的垂直平分线m.n,交于O点;
2.以O为圆心,OA为半径作圆。
你能破镜重圆吗?
A
B
A
C
m
n
·
O
1.作弦AB.AC及它们的垂直平分线m.n,交于O点;
2.以O为圆心,OA为半径作圆。
课堂总结
回顾与思考
1.圆的基本性质:(1)圆的中心对称性(2)圆的轴对称性(3)圆的旋转不变性
4.垂径定理及推论的应用:(1)计算(2)证明(3)作图
2.垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧
3.垂径定理的推论:
(1)推论1① 平分弦(不是直径)的直径垂直与弦并且平分弦所对的两条弧。
②弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
③平分弦所对的一条弧的直径垂直平分弦,并且平分弦所对的另一条弧。
(2)推论2:圆内的两条平行弦所夹的弧相等。
作业:
教材
3.4.5
再 见
谢谢大家
