山西省怀仁市大地高级中学2020-2021学年高一下学期第三次月考(5月)数学试题 Word版含答案
文档属性
| 名称 | 山西省怀仁市大地高级中学2020-2021学年高一下学期第三次月考(5月)数学试题 Word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-01 08:03:19 | ||
图片预览



文档简介
绝密★启用前
怀仁市大地高级中学2020-2021学年度下学期第三次月考
高一数学
(考试时间:120分钟 试卷满分:150分)
注意事项:
1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2. 回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。
3. 回答第Ⅱ卷时,将答案写在答题卡上。写在本试卷上无效。
4. 考试结束后,将答题卡交回。
第Ⅰ卷
一、选择题(本题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 复数(位虚数单位)在复平面内对应的点位于
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 在某次测量中得到的A样本数据如下:42,43,46,52,42,50,若B样本数据恰好是A样本数据每个都减5后所得数据,则A、B两样本的下列数字特征对应相同的是
A. 平均数 B. 标准差 C. 众数 D. 中位数
3. 已知一个三棱柱的高为3,如图是其底面用斜二测画法画出的水平放置的直观图,其中,则此三棱柱的体积为
A. 2 B. 4 C. 6 D. 12
4. 已知非零向量,若,且,则的夹角为
A. B. C. D.
5. 设为平面,为两条不同的直线,则下列叙述正确的是
A. 若∥,∥,则∥ B. 若,∥,则
C. 若,,则∥ D. 若∥,,则
6. 已知圆锥的顶点为,母线,所成角的余弦值为,与圆锥底面所成角为,若的面积为,则该圆锥的体积为
A. B. C. D.
7. 已知数据的方差为4,若,则新数据的方差为
A. 16 B. 13 C. -8 D. -16.
8. 如图是一个正方体的表面展开图,则图中“有”在正方体中所在的面的对面上的是
A. 者 B. 事 C. 竟 D. 成
9. 已知向量不共线,,,若∥,则
A. ﹣12 B. ﹣9 C. ﹣6 D. ﹣3
10. 如图所示是一样本的频率分布直方图,样本数据共分3组,分别为[5,10),[10,15),[15,20]. 估计样本数据的第60百分位数是
A. 14 B. 15 C. 16 D. 17
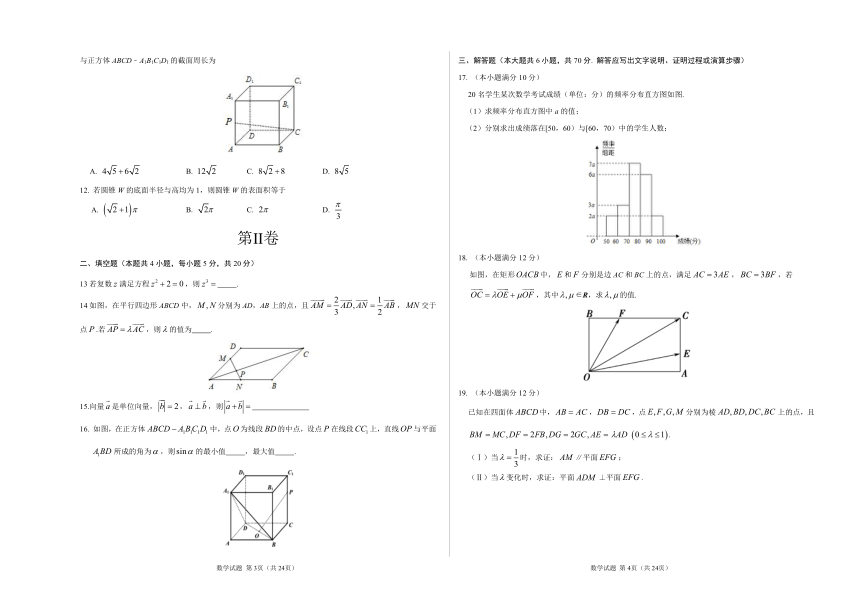
11. 已知正方体ABCD﹣A1B1C1D1棱长为4,P是AA1中点,过点D1作平面,满足CP⊥平面,则平面与正方体ABCD﹣A1B1C1D1的截面周长为
A. B. C. D.
12. 若圆锥W的底面半径与高均为1,则圆锥W的表面积等于
A. B. C. D.
第Ⅱ卷
二、填空题(本题共4小题,每小题5分,共20分)
13若复数满足方程,则??????????.
14如图,在平行四边形ABCD中,分别为AD,AB上的点,且,交于点.若,则的值为??????????.
15.向量是单位向量,,,则
16. 如图,在正方体中,点为线段的中点,设点在线段上,直线与平面所成的角为,则的最小值??????????,最大值??????????.
三、解答题(本大题共6小题,共70分. 解答应写出文字说明、证明过程或演算步骤)
17. (本小题满分10分)
20名学生某次数学考试成绩(单位:分)的频率分布直方图如图.
(1)求频率分布直方图中a的值;
(2)分别求出成绩落在[50,60)与[60,70)中的学生人数;
18. (本小题满分12分)
如图,在矩形中,和分别是边AC和BC上的点,满足,,若,其中∈R,求的值.
19. (本小题满分12分)
已知在四面体中,,,点分别为棱上的点,且.
(Ⅰ)当时,求证:∥平面;
(Ⅱ)当变化时,求证:平面⊥平面.
20. (本小题满分12分)
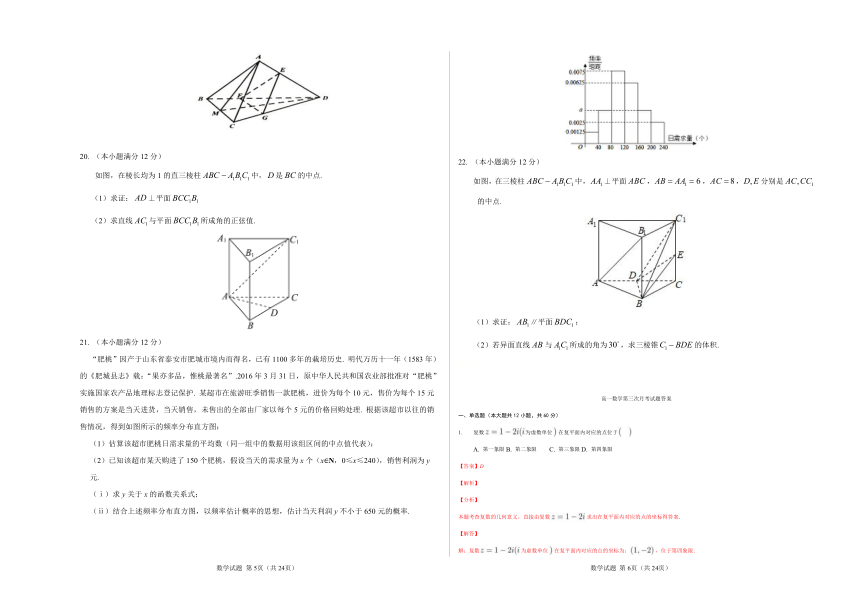
如图,在棱长均为1的直三棱柱中,是的中点.
(1)求证:⊥平面
(2)求直线与平面所成角的正弦值.
21. (本小题满分12分)
“肥桃”因产于山东省泰安市肥城市境内而得名,已有1100多年的栽培历史. 明代万历十一年(1583年)的《肥城县志》载:“果亦多品,惟桃最著名”.2016年3月31日,原中华人民共和国农业部批准对“肥桃”实施国家农产品地理标志登记保护. 某超市在旅游旺季销售一款肥桃,进价为每个10元,售价为每个15元销售的方案是当天进货,当天销售,未售出的全部由厂家以每个5元的价格回购处理. 根据该超市以往的销售情况,得到如图所示的频率分布直方图:
(1)估算该超市肥桃日需求量的平均数(同一组中的数据用该组区间的中点值代表);
(2)已知该超市某天购进了150个肥桃,假设当天的需求量为x个(x∈N,0≤x≤240),销售利润为y元.
(ⅰ)求y关于x的函数关系式;
(ⅱ)结合上述频率分布直方图,以频率估计概率的思想,估计当天利润y不小于650元的概率.
22. (本小题满分12分)
如图,在三棱柱中,⊥平面,,,分别是 的中点.
(1)求证:∥平面;
(2)若异面直线与所成的角为,求三棱锥的体积.
高一数学第三次月考试题答案
一、单选题(本大题共12小题,共60分)
复数为虚数单位在复平面内对应的点位于
A. 第一象限B. 第二象限 C. 第三象限D. 第四象限
【答案】D
【解析】
【分析】
本题考查复数的几何意义,直接由复数求出在复平面内对应的点的坐标得答案.
【解答】
解:复数为虚数单位在复平面内对应的点的坐标为:,位于第四象限.
故选D.
2在某次测量中得到的A样本数据如下:42,43,46,52,42,50,若B样本数据恰好是A样本数据每个都减5后所得数据,则A、B两样本的下列数字特征对应相同的是( )
A.平均数B.标准差C.众数D.中位数
【分析】根据样本A,B中数据之间的关系,结合众数,平均数,中位数和标准差的定义即可得到结论.
【解答】解:设样本A中的数据为xi,则样本B中的数据为yi=xi﹣5,
则样本数据B中的众数和平均数以及中位数和A中的众数,平均数,中位数相差5,
只有标准差没有发生变化,
故选:B.
3已知一个三棱柱的高为3,如图是其底面用斜二测画法画出的水平放置的直观图,其中,则此三棱柱的体积为
A. 2
B. 4
C. 6
D. 12
【答案】C
【解析】
【分析】
本题考察直观图与原图的关系,以及棱柱的体积公式,属于基础题.
依据直观图可知原图的底面三角形的底边长为2,高为2,可求出柱体的底面面积,再依据棱柱体积公式可求出答案.
【解答】
解:设三棱柱的底面三角形为,由直观图可知,,
且,,
故.
故答案选C.
4已知非零向量,,若,且,则与的夹角为
A. B. C. D.
【答案】B
【解析】
【分析】
本题考查了向量的数量积,考查了向量垂直的关系,考查了向量夹角的求解本题的关键是由垂直求出数量积为0.
由向量垂直可得,结合数量积的定义表达式可求出,又,从而可求出夹角的余弦值,进而可求夹角的大小.
【解答】
解:因为,
所以,
因为,
所以,
.
故选:B.
5设为平面,a,b为两条不同的直线,则下列叙述正确的是
若,,则B. 若,,则
C. 若,,则D. 若,,则
【答案】B
【解析】
【分析】
本题考查命题的真假的判断,是基础题,解题时要认真审题,注意空间思维能力的培养.
利用空间线线、线面、面面间的关系对每一个选项逐一分析判断得解.
【解答】
解:若,,则a与b相交、平行或异面,故A错误;
若,,则由直线与平面垂直的判定定理知,故B正确;
若,,则或,故C错误;
若,,则,或,或b与相交,故D错误.
故选:B.
6已知圆锥的顶点为P,母线PA,PB所成角的余弦值为,PA与圆锥底面所成角为,若的面积为,则该圆锥的体积为
A. B. C. D.
【答案】C
【解析】
【分析】
本题考查线面角的概念、三角形面积公式、圆锥的体积公式,考查转化与化归思想,考查空间想象能力、运算求解能力.
设底面半径为,根据线面角的大小可得母线长为2r,再根据三角形的面积得到r的值,最后代入圆锥的体积公式,即可得答案.
【解答】
解:如图所示,设底面半径为,
与圆锥底面所成角为,,
,母线PA,PB所成角的余弦值为,
,,
,
故选:C.
7已知数据的方差为4,若,则新数据的方差为
A. 16B. 13C. D.
【答案】A
【解析】
【分析】
本题考查利用方差的性质求解方差的问题,属于基础题.
根据方差的性质直接计算可得结果.
【解答】
解:由方差的性质知:新数据的方差为:.
故选:A.
8.如图是一个正方体的表面展开图,则图中“有”在正方体中所在的面的对面上的是( )
A.者B.事C.竟D.成
【分析】直接把正方体的展开面图复原为空间图,进一步求出结果.
【解答】解:根据正方体的表面展开图,复原成正方体.
如图所示:
其中“者”在最里面,“有”在最外面.构成对面关系.
故选:A.
9.已知向量不共线,,,若,则m=( )
A.﹣12B.﹣9C.﹣6D.﹣3
【分析】由向量平行的性质得3+=λm+λ(m+2),由此能求出m.
【解答】解:∵向量不共线,,,,
∴3+=λm+λ(m+2),
∴,
解得λ=﹣1,m=﹣3.
故选:D.
10.如图所示是一样本的频率分布直方图,样本数据共分3组,分别为[5,10),[10,15),[15,20].估计样本数据的第60百分位数是( )
A.14B.15C.16 D.17
【分析】由频率分布直方图,根据样本数据的百分位数列方程求出即可.
【解答】解:由频率分布直方图知,第1组的频率为0.04×5=0.2,
第2组的频率为0.10×5=0.5,
设样本数据的第60百分位数是x,则0.2+0.10(x﹣10)=0.6,
解得x=14,
所以估计样本数据的第60百分位数是14.
故选:A.
11.已知正方体ABCD﹣A1B1C1D1棱长为4,P是AA1中点,过点D1作平面α,满足CP⊥平面α,则平面α与正方体ABCD﹣A1B1C1D1的截面周长为( )
A.4B.12 C.8D.8
【分析】取 AD 中点 E,AB 中点 F,连接PD,D1E,EF,B1F,B1D1,AC,先证明 E,F,B1,D1四点共面,再由 EF⊥CP,D1E⊥CP 证明 CP⊥平面 EFB1D1可知平面 EFB1D1为平面 α 与正方体 ABCD﹣A1B1C1D1的截面,根据正方体的棱长即可求得 EFB1D1的周长.
【解答】解:取 AD 中点 E,AB 中点 F,连接PD,D1E,EF,B1F,B1D1,AC,
如下图所示:
E 为 AD 中点,F 为 AB 中点,则 EF∥BD,BD∥B1D1
所以 EF∥B1D1
所以 E,F,B1,D1四点共面.
根据正方形性质可知 CD⊥平面 ADD1A1,
而 D1E?平面ADD1A1,所以 CD⊥D1E,
A△D1DE≌△DAP,可知∠ED1D=∠PDA,
而∠PDA+∠PDD1=90°,所以∠ED1D+∠PDD1=90°,
即 PD⊥D1E
为 CD∩PD=D,所以 D1E⊥平面 PDC,
而CP?平面 PDC,所以 D1E⊥CP;
E 为 AD 中点,F 为 AB 中点,由正方形和正方体性质可知
EF⊥AC,PA⊥EF,且 PA∩AC=A,
所以 EF⊥平面 PAC,而 CP?平面 PDC,
所以 EF⊥CP,又因为 D1E⊥CP,D1E∩EF=E
所以 CP⊥平面 EFB1D1
即平面 EFB1D1为平面 α 与正方体 ABCD﹣A1B1C1D1的截面,
正方体 ABCD﹣A1B1C1D1棱长为 4
所以 EFB1D1的周长为 B1D1+D1E+EF+B1F
=
=,
故选:A.
12.若圆锥W的底面半径与高均为1,则圆锥W的表面积等于( )
A. B.C.2π D.
【分析】求出圆锥的母线长,再计算圆锥的侧面积和表面积.
【解答】解:圆锥的轴截面如图所示,
则圆锥的母线为l==,
所以该圆锥的侧面积为S侧面积=πrl=π?1?=π,
圆锥的表面积为S表面积=S侧面积+S底面积=π+π?12=(+1)π.
故选:A.
二、填空题(本大题共4小题,共20分)
13若复数z满足方程,则 .
【答案】
【解析】
【分析】
本题考查复数的计算,属基础题.
根据题意可得,然后根据复数的乘法可得结果.
【解答】
解:由,则,
所以,
所以,
故答案为:
14如图,在平行四边形ABCD中,M,N分别为AD,AB上的点,且,MN交于点若,则的值为 .
【答案】
【解析】
【分析】
本题考查平面向量共线定理的推论,涉及向量的线性运算,属基础题.
用向量表示,结合三点共线,即可求得参数值.
【解答】
解:根据题意,
,
因为三点共线,
所以,解得.
故答案为.
15.向量是单位向量,||=2,⊥,则||= .
【分析】由题意可得,进行向量的模的运算带入求值即可得答案.
【解答】解:∵?;
∴||==.
故答案为:.
16如图,在正方体中,点O为线段BD的中点,设点P在线段上,直线OP与平面所成的角为,则的最小值 ,最大值 .
【答案】,1
1
【解析】
【分析】
此题考查正方体的性质和直角三角形的边角关系,线面角的求法,考查推理能力,属于中档题。
由题意,直线OP与平面所成的角的最小值为和中的最小者,然后利用正方体的性质和直角三角形的边角关系,求出的取值范围,再确定其最值
【解答】
解:连接,,
因为,平面,
所以平面,
又平面
所以平面平面,
所以直线OP与平面所成的角的最小值为和中的最小者,
不妨设,
在中,,
,
所以的取值范围为,
所以的最小值为,最大值为1,
故答案为:;1.
三、解答题(本大题共6小题,共70分)
22(10分).20名学生某次数学考试成绩(单位:分)的频率分布直方图如图.
(1)求频率分布直方图中a的值;
(2)分别求出成绩落在[50,60)与[60,70)中的学生人数;
【分析】(1)根据频率分布直方图求出a的值;
(2)由图可知,成绩在[50,60)和[60,70)的频率分别为0.1和0.15,用样本容量20乘以对应的频率,即得对应区间内的人数,从而求出所求.
【解答】解:(1)根据直方图知组距=10,由(2a+3a+6a+7a+2a)×10=1,解得a=0.005.
(2)成绩落在[50,60)中的学生人数为2×0.005×10×20=2,
成绩落在[60,70)中的学生人数为3×0.005×10×20=3.
17(12分)如图,在矩形OACB中,E和F分别是边AC和BC上的点,满足,,若,其中,R,求,的值.
【答案】解:因为,,
在矩形OACB中,,
又
,
所以,,
所以.
【解析】本题考查平面向量基本定理,属于基础题.
根据题意得出,则,由此即可求出结果.
18(12分).已知在四面体ABCD中,AB=AC,DB=DC,点E,F,G,M分别为棱AD,BD,DC,BC上的点,且BM=MC,DF=2FB,DG=2GC,AE=λAD(0≤λ≤1).
(Ⅰ)当λ=时,求证:AM∥平面EFG;
(Ⅱ)当λ变化时,求证:平面ADM⊥平面EFG.
【分析】(Ⅰ)当λ=时,,推导出EF∥AB,EG∥AC,从而平面ABC∥平面EFG,由此能证明AM∥平面EFG.
(Ⅱ)推导出AM⊥BC,DM⊥BC,BC∥GF,从而BC⊥平面ADM,GF⊥平面ADM,由此能证明当λ变化时,平面ADM⊥平面EFG.
【解答】证明:(Ⅰ)当λ=时,,
∵四面体ABCD中,AB=AC,DB=DC,
点E,F,G,M分别为棱AD,BD,DC,BC上的点,BM=MC,DF=2FB,DG=2GC,
∴EF∥AB,EG∥AC,又EF∩EG=E,AB∩AC=A,
∴平面ABC∥平面EFG,
∵AM?平面ABC,∴AM∥平面EFG.
(Ⅱ)∵AB=AC,DB=DC,点E,F,G,M分别为棱AD,BD,DC,BC上的点,
BM=MC,DF=2FB,DG=2GC,AE=λAD(0≤λ≤1).
∴AM⊥BC,DM⊥BC,BC∥GF,
∵AM∩DM=M,∴BC⊥平面ADM,
∵GF∥BC,∴GF⊥平面ADM,
∵GF?平面EFG,
∴当λ变化时,平面ADM⊥平面EFG.
19(12分)如图,在棱长均为1的直三棱柱中,D是BC的中点.
求证:平面
求直线与平面所成角的正弦值.
【答案】证明:直三棱柱中,平面ABC,平面ABC,
,
,D是BC的中点,
,
又,BC、平面,
平面.
解:如图,连接,
由可知,平面,
则即为直线与平面所成角,
因为平面,平面,
所以,
在中,,,
所以,
所以直线与平面所成角的正弦值为.
【解析】本题考查线面垂直的判定,直线与平面所成角,属于中档题.
由题意,可得到,并且,从而由线面垂直的判定定理可得到平面;
连接,可得到为直线和平面所成角,即可得解.
本题考查线面垂直的判定,直线与平面所成角,属于中档题.
由题意,可得到,并且,从而由线面垂直的判定定理可得到平面;
连接,可得到为直线和平面所成角,即可得解.
20(12分)“肥桃”因产于山东省泰安市肥城市境内而得名,已有1100多年的栽培历史.明代万历十一年(1583年)的《肥城县志》载:“果亦多品,惟桃最著名”.2016年3月31日,原中华人民共和国农业部批准对“肥桃”实施国家农产品地理标志登记保护.某超市在旅游旺季销售一款肥桃,进价为每个10元,售价为每个15元销售的方案是当天进货,当天销售,未售出的全部由厂家以每个5元的价格回购处理.根据该超市以往的销售情况,得到如图所示的频率分布直方图:
(1)估算该超市肥桃日需求量的平均数(同一组中的数据用该组区间的中点值代表);
(2)已知该超市某天购进了150个肥桃,假设当天的需求量为x个(x∈N,0≤x≤240),销售利润为y元.
(ⅰ)求y关于x的函数关系式;
(ⅱ)结合上述频率分布直方图,以频率估计概率的思想,估计当天利润y不小于650元的概率.
【分析】(1)先利用各组频率之和为1,求出a的值,再利用每组区间的中点值乘以该组的频率依次相加,即可估算出平均数;
(2)( i)分情况讨论,得到y关于x的分段函数的函数关系式即可;( ii)利润y≥650,当且仅当日需求量x∈[140,240]. 由频率分布直方图求出x∈[140,240]的频率,以频率估计概率的思想,能估计当天利润y不小于650元的概率.
【解答】解:(1)由题意可知:(0.00125+a+0.0075+0.00625+a+0.0025)×40=1,
解得a=0.00375;
所以平均数 =(20×0.00125+60×0.00375+100×0.0075+140×0.00625+180×0.00375+220×0.0025)×40
=0.05×20+0.15×60+0.3×100+0.25×140+0.15×180+0.1×220=124;
(2)( i)当x∈[150,240]时,y=150×(20﹣15)=750,
当x∈[0,150)时,y=(20﹣15)x﹣(150﹣x)(15﹣10)=10x﹣750,
故y=,(x∈N);
( ii)由( i)可知,利润y≥650,当且仅当日需求量x∈[140,240].
由频率分布直方图可知,日需求量x∈[140,240]的频率约为 0.125+0.15+0.1=0.375,
以频率估计概率的思想,估计当天利润y不小于650元的概率为0.375.
21(12分).如图,在三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,AB=AA1=6,AC=8,D,E分别是AC,CC1的中点.
(1)求证:AB1∥平面BDC1;
(2)若异面直线AB与A1C1所成的角为30°,求三棱锥C1﹣BDE的体积.
【分析】(1)如图,连接B1C,交BC1于点F,连接DF,由已知结合三角形中位线定理可得DF∥AB1,再由直线与平面平行的判定定理,证明AB1∥平面BDC1;
(2)由AC∥A1C1,可得∠BAC即为异面直线AB与A1C1所成的角为30°,求三角形ABC的面积,得到三角形DBC的面积,然后分别求出三棱锥C1﹣BCD,E﹣BCD的体积,再由求解.
【解答】解:(1)证明:如图,连接B1C,交BC1于点F,连接DF,
在△ACB1中,由于D为AC的中点,F为B1C的中点
∴DF为△ACB1的中位线,∴DF∥AB1,
∵DF?平面BDC1,AB1?平面BDC1,
∴AB1∥平面BDC1;
(2)∵AC∥A1C1,∴∠BAC即为异面直线AB与A1C1所成的角,
∵异面直线AB与A1C1所成的角为30°,∴∠BAC=30°,
∴,
∵D是AC的中点,∴,
又∵CC1⊥平面ABC,CC1=6,E是CC1的中点.
∴.
,
∴.
即三棱锥C1﹣BDE的体积为6.
数学试题 第1*2-1 11页(共12*2 1224页) 数学试题 第1*2 12页(共12*2 1224页)
怀仁市大地高级中学2020-2021学年度下学期第三次月考
高一数学
(考试时间:120分钟 试卷满分:150分)
注意事项:
1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2. 回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。
3. 回答第Ⅱ卷时,将答案写在答题卡上。写在本试卷上无效。
4. 考试结束后,将答题卡交回。
第Ⅰ卷
一、选择题(本题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 复数(位虚数单位)在复平面内对应的点位于
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 在某次测量中得到的A样本数据如下:42,43,46,52,42,50,若B样本数据恰好是A样本数据每个都减5后所得数据,则A、B两样本的下列数字特征对应相同的是
A. 平均数 B. 标准差 C. 众数 D. 中位数
3. 已知一个三棱柱的高为3,如图是其底面用斜二测画法画出的水平放置的直观图,其中,则此三棱柱的体积为
A. 2 B. 4 C. 6 D. 12
4. 已知非零向量,若,且,则的夹角为
A. B. C. D.
5. 设为平面,为两条不同的直线,则下列叙述正确的是
A. 若∥,∥,则∥ B. 若,∥,则
C. 若,,则∥ D. 若∥,,则
6. 已知圆锥的顶点为,母线,所成角的余弦值为,与圆锥底面所成角为,若的面积为,则该圆锥的体积为
A. B. C. D.
7. 已知数据的方差为4,若,则新数据的方差为
A. 16 B. 13 C. -8 D. -16.
8. 如图是一个正方体的表面展开图,则图中“有”在正方体中所在的面的对面上的是
A. 者 B. 事 C. 竟 D. 成
9. 已知向量不共线,,,若∥,则
A. ﹣12 B. ﹣9 C. ﹣6 D. ﹣3
10. 如图所示是一样本的频率分布直方图,样本数据共分3组,分别为[5,10),[10,15),[15,20]. 估计样本数据的第60百分位数是
A. 14 B. 15 C. 16 D. 17
11. 已知正方体ABCD﹣A1B1C1D1棱长为4,P是AA1中点,过点D1作平面,满足CP⊥平面,则平面与正方体ABCD﹣A1B1C1D1的截面周长为
A. B. C. D.
12. 若圆锥W的底面半径与高均为1,则圆锥W的表面积等于
A. B. C. D.
第Ⅱ卷
二、填空题(本题共4小题,每小题5分,共20分)
13若复数满足方程,则??????????.
14如图,在平行四边形ABCD中,分别为AD,AB上的点,且,交于点.若,则的值为??????????.
15.向量是单位向量,,,则
16. 如图,在正方体中,点为线段的中点,设点在线段上,直线与平面所成的角为,则的最小值??????????,最大值??????????.
三、解答题(本大题共6小题,共70分. 解答应写出文字说明、证明过程或演算步骤)
17. (本小题满分10分)
20名学生某次数学考试成绩(单位:分)的频率分布直方图如图.
(1)求频率分布直方图中a的值;
(2)分别求出成绩落在[50,60)与[60,70)中的学生人数;
18. (本小题满分12分)
如图,在矩形中,和分别是边AC和BC上的点,满足,,若,其中∈R,求的值.
19. (本小题满分12分)
已知在四面体中,,,点分别为棱上的点,且.
(Ⅰ)当时,求证:∥平面;
(Ⅱ)当变化时,求证:平面⊥平面.
20. (本小题满分12分)
如图,在棱长均为1的直三棱柱中,是的中点.
(1)求证:⊥平面
(2)求直线与平面所成角的正弦值.
21. (本小题满分12分)
“肥桃”因产于山东省泰安市肥城市境内而得名,已有1100多年的栽培历史. 明代万历十一年(1583年)的《肥城县志》载:“果亦多品,惟桃最著名”.2016年3月31日,原中华人民共和国农业部批准对“肥桃”实施国家农产品地理标志登记保护. 某超市在旅游旺季销售一款肥桃,进价为每个10元,售价为每个15元销售的方案是当天进货,当天销售,未售出的全部由厂家以每个5元的价格回购处理. 根据该超市以往的销售情况,得到如图所示的频率分布直方图:
(1)估算该超市肥桃日需求量的平均数(同一组中的数据用该组区间的中点值代表);
(2)已知该超市某天购进了150个肥桃,假设当天的需求量为x个(x∈N,0≤x≤240),销售利润为y元.
(ⅰ)求y关于x的函数关系式;
(ⅱ)结合上述频率分布直方图,以频率估计概率的思想,估计当天利润y不小于650元的概率.
22. (本小题满分12分)
如图,在三棱柱中,⊥平面,,,分别是 的中点.
(1)求证:∥平面;
(2)若异面直线与所成的角为,求三棱锥的体积.
高一数学第三次月考试题答案
一、单选题(本大题共12小题,共60分)
复数为虚数单位在复平面内对应的点位于
A. 第一象限B. 第二象限 C. 第三象限D. 第四象限
【答案】D
【解析】
【分析】
本题考查复数的几何意义,直接由复数求出在复平面内对应的点的坐标得答案.
【解答】
解:复数为虚数单位在复平面内对应的点的坐标为:,位于第四象限.
故选D.
2在某次测量中得到的A样本数据如下:42,43,46,52,42,50,若B样本数据恰好是A样本数据每个都减5后所得数据,则A、B两样本的下列数字特征对应相同的是( )
A.平均数B.标准差C.众数D.中位数
【分析】根据样本A,B中数据之间的关系,结合众数,平均数,中位数和标准差的定义即可得到结论.
【解答】解:设样本A中的数据为xi,则样本B中的数据为yi=xi﹣5,
则样本数据B中的众数和平均数以及中位数和A中的众数,平均数,中位数相差5,
只有标准差没有发生变化,
故选:B.
3已知一个三棱柱的高为3,如图是其底面用斜二测画法画出的水平放置的直观图,其中,则此三棱柱的体积为
A. 2
B. 4
C. 6
D. 12
【答案】C
【解析】
【分析】
本题考察直观图与原图的关系,以及棱柱的体积公式,属于基础题.
依据直观图可知原图的底面三角形的底边长为2,高为2,可求出柱体的底面面积,再依据棱柱体积公式可求出答案.
【解答】
解:设三棱柱的底面三角形为,由直观图可知,,
且,,
故.
故答案选C.
4已知非零向量,,若,且,则与的夹角为
A. B. C. D.
【答案】B
【解析】
【分析】
本题考查了向量的数量积,考查了向量垂直的关系,考查了向量夹角的求解本题的关键是由垂直求出数量积为0.
由向量垂直可得,结合数量积的定义表达式可求出,又,从而可求出夹角的余弦值,进而可求夹角的大小.
【解答】
解:因为,
所以,
因为,
所以,
.
故选:B.
5设为平面,a,b为两条不同的直线,则下列叙述正确的是
若,,则B. 若,,则
C. 若,,则D. 若,,则
【答案】B
【解析】
【分析】
本题考查命题的真假的判断,是基础题,解题时要认真审题,注意空间思维能力的培养.
利用空间线线、线面、面面间的关系对每一个选项逐一分析判断得解.
【解答】
解:若,,则a与b相交、平行或异面,故A错误;
若,,则由直线与平面垂直的判定定理知,故B正确;
若,,则或,故C错误;
若,,则,或,或b与相交,故D错误.
故选:B.
6已知圆锥的顶点为P,母线PA,PB所成角的余弦值为,PA与圆锥底面所成角为,若的面积为,则该圆锥的体积为
A. B. C. D.
【答案】C
【解析】
【分析】
本题考查线面角的概念、三角形面积公式、圆锥的体积公式,考查转化与化归思想,考查空间想象能力、运算求解能力.
设底面半径为,根据线面角的大小可得母线长为2r,再根据三角形的面积得到r的值,最后代入圆锥的体积公式,即可得答案.
【解答】
解:如图所示,设底面半径为,
与圆锥底面所成角为,,
,母线PA,PB所成角的余弦值为,
,,
,
故选:C.
7已知数据的方差为4,若,则新数据的方差为
A. 16B. 13C. D.
【答案】A
【解析】
【分析】
本题考查利用方差的性质求解方差的问题,属于基础题.
根据方差的性质直接计算可得结果.
【解答】
解:由方差的性质知:新数据的方差为:.
故选:A.
8.如图是一个正方体的表面展开图,则图中“有”在正方体中所在的面的对面上的是( )
A.者B.事C.竟D.成
【分析】直接把正方体的展开面图复原为空间图,进一步求出结果.
【解答】解:根据正方体的表面展开图,复原成正方体.
如图所示:
其中“者”在最里面,“有”在最外面.构成对面关系.
故选:A.
9.已知向量不共线,,,若,则m=( )
A.﹣12B.﹣9C.﹣6D.﹣3
【分析】由向量平行的性质得3+=λm+λ(m+2),由此能求出m.
【解答】解:∵向量不共线,,,,
∴3+=λm+λ(m+2),
∴,
解得λ=﹣1,m=﹣3.
故选:D.
10.如图所示是一样本的频率分布直方图,样本数据共分3组,分别为[5,10),[10,15),[15,20].估计样本数据的第60百分位数是( )
A.14B.15C.16 D.17
【分析】由频率分布直方图,根据样本数据的百分位数列方程求出即可.
【解答】解:由频率分布直方图知,第1组的频率为0.04×5=0.2,
第2组的频率为0.10×5=0.5,
设样本数据的第60百分位数是x,则0.2+0.10(x﹣10)=0.6,
解得x=14,
所以估计样本数据的第60百分位数是14.
故选:A.
11.已知正方体ABCD﹣A1B1C1D1棱长为4,P是AA1中点,过点D1作平面α,满足CP⊥平面α,则平面α与正方体ABCD﹣A1B1C1D1的截面周长为( )
A.4B.12 C.8D.8
【分析】取 AD 中点 E,AB 中点 F,连接PD,D1E,EF,B1F,B1D1,AC,先证明 E,F,B1,D1四点共面,再由 EF⊥CP,D1E⊥CP 证明 CP⊥平面 EFB1D1可知平面 EFB1D1为平面 α 与正方体 ABCD﹣A1B1C1D1的截面,根据正方体的棱长即可求得 EFB1D1的周长.
【解答】解:取 AD 中点 E,AB 中点 F,连接PD,D1E,EF,B1F,B1D1,AC,
如下图所示:
E 为 AD 中点,F 为 AB 中点,则 EF∥BD,BD∥B1D1
所以 EF∥B1D1
所以 E,F,B1,D1四点共面.
根据正方形性质可知 CD⊥平面 ADD1A1,
而 D1E?平面ADD1A1,所以 CD⊥D1E,
A△D1DE≌△DAP,可知∠ED1D=∠PDA,
而∠PDA+∠PDD1=90°,所以∠ED1D+∠PDD1=90°,
即 PD⊥D1E
为 CD∩PD=D,所以 D1E⊥平面 PDC,
而CP?平面 PDC,所以 D1E⊥CP;
E 为 AD 中点,F 为 AB 中点,由正方形和正方体性质可知
EF⊥AC,PA⊥EF,且 PA∩AC=A,
所以 EF⊥平面 PAC,而 CP?平面 PDC,
所以 EF⊥CP,又因为 D1E⊥CP,D1E∩EF=E
所以 CP⊥平面 EFB1D1
即平面 EFB1D1为平面 α 与正方体 ABCD﹣A1B1C1D1的截面,
正方体 ABCD﹣A1B1C1D1棱长为 4
所以 EFB1D1的周长为 B1D1+D1E+EF+B1F
=
=,
故选:A.
12.若圆锥W的底面半径与高均为1,则圆锥W的表面积等于( )
A. B.C.2π D.
【分析】求出圆锥的母线长,再计算圆锥的侧面积和表面积.
【解答】解:圆锥的轴截面如图所示,
则圆锥的母线为l==,
所以该圆锥的侧面积为S侧面积=πrl=π?1?=π,
圆锥的表面积为S表面积=S侧面积+S底面积=π+π?12=(+1)π.
故选:A.
二、填空题(本大题共4小题,共20分)
13若复数z满足方程,则 .
【答案】
【解析】
【分析】
本题考查复数的计算,属基础题.
根据题意可得,然后根据复数的乘法可得结果.
【解答】
解:由,则,
所以,
所以,
故答案为:
14如图,在平行四边形ABCD中,M,N分别为AD,AB上的点,且,MN交于点若,则的值为 .
【答案】
【解析】
【分析】
本题考查平面向量共线定理的推论,涉及向量的线性运算,属基础题.
用向量表示,结合三点共线,即可求得参数值.
【解答】
解:根据题意,
,
因为三点共线,
所以,解得.
故答案为.
15.向量是单位向量,||=2,⊥,则||= .
【分析】由题意可得,进行向量的模的运算带入求值即可得答案.
【解答】解:∵?;
∴||==.
故答案为:.
16如图,在正方体中,点O为线段BD的中点,设点P在线段上,直线OP与平面所成的角为,则的最小值 ,最大值 .
【答案】,1
1
【解析】
【分析】
此题考查正方体的性质和直角三角形的边角关系,线面角的求法,考查推理能力,属于中档题。
由题意,直线OP与平面所成的角的最小值为和中的最小者,然后利用正方体的性质和直角三角形的边角关系,求出的取值范围,再确定其最值
【解答】
解:连接,,
因为,平面,
所以平面,
又平面
所以平面平面,
所以直线OP与平面所成的角的最小值为和中的最小者,
不妨设,
在中,,
,
所以的取值范围为,
所以的最小值为,最大值为1,
故答案为:;1.
三、解答题(本大题共6小题,共70分)
22(10分).20名学生某次数学考试成绩(单位:分)的频率分布直方图如图.
(1)求频率分布直方图中a的值;
(2)分别求出成绩落在[50,60)与[60,70)中的学生人数;
【分析】(1)根据频率分布直方图求出a的值;
(2)由图可知,成绩在[50,60)和[60,70)的频率分别为0.1和0.15,用样本容量20乘以对应的频率,即得对应区间内的人数,从而求出所求.
【解答】解:(1)根据直方图知组距=10,由(2a+3a+6a+7a+2a)×10=1,解得a=0.005.
(2)成绩落在[50,60)中的学生人数为2×0.005×10×20=2,
成绩落在[60,70)中的学生人数为3×0.005×10×20=3.
17(12分)如图,在矩形OACB中,E和F分别是边AC和BC上的点,满足,,若,其中,R,求,的值.
【答案】解:因为,,
在矩形OACB中,,
又
,
所以,,
所以.
【解析】本题考查平面向量基本定理,属于基础题.
根据题意得出,则,由此即可求出结果.
18(12分).已知在四面体ABCD中,AB=AC,DB=DC,点E,F,G,M分别为棱AD,BD,DC,BC上的点,且BM=MC,DF=2FB,DG=2GC,AE=λAD(0≤λ≤1).
(Ⅰ)当λ=时,求证:AM∥平面EFG;
(Ⅱ)当λ变化时,求证:平面ADM⊥平面EFG.
【分析】(Ⅰ)当λ=时,,推导出EF∥AB,EG∥AC,从而平面ABC∥平面EFG,由此能证明AM∥平面EFG.
(Ⅱ)推导出AM⊥BC,DM⊥BC,BC∥GF,从而BC⊥平面ADM,GF⊥平面ADM,由此能证明当λ变化时,平面ADM⊥平面EFG.
【解答】证明:(Ⅰ)当λ=时,,
∵四面体ABCD中,AB=AC,DB=DC,
点E,F,G,M分别为棱AD,BD,DC,BC上的点,BM=MC,DF=2FB,DG=2GC,
∴EF∥AB,EG∥AC,又EF∩EG=E,AB∩AC=A,
∴平面ABC∥平面EFG,
∵AM?平面ABC,∴AM∥平面EFG.
(Ⅱ)∵AB=AC,DB=DC,点E,F,G,M分别为棱AD,BD,DC,BC上的点,
BM=MC,DF=2FB,DG=2GC,AE=λAD(0≤λ≤1).
∴AM⊥BC,DM⊥BC,BC∥GF,
∵AM∩DM=M,∴BC⊥平面ADM,
∵GF∥BC,∴GF⊥平面ADM,
∵GF?平面EFG,
∴当λ变化时,平面ADM⊥平面EFG.
19(12分)如图,在棱长均为1的直三棱柱中,D是BC的中点.
求证:平面
求直线与平面所成角的正弦值.
【答案】证明:直三棱柱中,平面ABC,平面ABC,
,
,D是BC的中点,
,
又,BC、平面,
平面.
解:如图,连接,
由可知,平面,
则即为直线与平面所成角,
因为平面,平面,
所以,
在中,,,
所以,
所以直线与平面所成角的正弦值为.
【解析】本题考查线面垂直的判定,直线与平面所成角,属于中档题.
由题意,可得到,并且,从而由线面垂直的判定定理可得到平面;
连接,可得到为直线和平面所成角,即可得解.
本题考查线面垂直的判定,直线与平面所成角,属于中档题.
由题意,可得到,并且,从而由线面垂直的判定定理可得到平面;
连接,可得到为直线和平面所成角,即可得解.
20(12分)“肥桃”因产于山东省泰安市肥城市境内而得名,已有1100多年的栽培历史.明代万历十一年(1583年)的《肥城县志》载:“果亦多品,惟桃最著名”.2016年3月31日,原中华人民共和国农业部批准对“肥桃”实施国家农产品地理标志登记保护.某超市在旅游旺季销售一款肥桃,进价为每个10元,售价为每个15元销售的方案是当天进货,当天销售,未售出的全部由厂家以每个5元的价格回购处理.根据该超市以往的销售情况,得到如图所示的频率分布直方图:
(1)估算该超市肥桃日需求量的平均数(同一组中的数据用该组区间的中点值代表);
(2)已知该超市某天购进了150个肥桃,假设当天的需求量为x个(x∈N,0≤x≤240),销售利润为y元.
(ⅰ)求y关于x的函数关系式;
(ⅱ)结合上述频率分布直方图,以频率估计概率的思想,估计当天利润y不小于650元的概率.
【分析】(1)先利用各组频率之和为1,求出a的值,再利用每组区间的中点值乘以该组的频率依次相加,即可估算出平均数;
(2)( i)分情况讨论,得到y关于x的分段函数的函数关系式即可;( ii)利润y≥650,当且仅当日需求量x∈[140,240]. 由频率分布直方图求出x∈[140,240]的频率,以频率估计概率的思想,能估计当天利润y不小于650元的概率.
【解答】解:(1)由题意可知:(0.00125+a+0.0075+0.00625+a+0.0025)×40=1,
解得a=0.00375;
所以平均数 =(20×0.00125+60×0.00375+100×0.0075+140×0.00625+180×0.00375+220×0.0025)×40
=0.05×20+0.15×60+0.3×100+0.25×140+0.15×180+0.1×220=124;
(2)( i)当x∈[150,240]时,y=150×(20﹣15)=750,
当x∈[0,150)时,y=(20﹣15)x﹣(150﹣x)(15﹣10)=10x﹣750,
故y=,(x∈N);
( ii)由( i)可知,利润y≥650,当且仅当日需求量x∈[140,240].
由频率分布直方图可知,日需求量x∈[140,240]的频率约为 0.125+0.15+0.1=0.375,
以频率估计概率的思想,估计当天利润y不小于650元的概率为0.375.
21(12分).如图,在三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,AB=AA1=6,AC=8,D,E分别是AC,CC1的中点.
(1)求证:AB1∥平面BDC1;
(2)若异面直线AB与A1C1所成的角为30°,求三棱锥C1﹣BDE的体积.
【分析】(1)如图,连接B1C,交BC1于点F,连接DF,由已知结合三角形中位线定理可得DF∥AB1,再由直线与平面平行的判定定理,证明AB1∥平面BDC1;
(2)由AC∥A1C1,可得∠BAC即为异面直线AB与A1C1所成的角为30°,求三角形ABC的面积,得到三角形DBC的面积,然后分别求出三棱锥C1﹣BCD,E﹣BCD的体积,再由求解.
【解答】解:(1)证明:如图,连接B1C,交BC1于点F,连接DF,
在△ACB1中,由于D为AC的中点,F为B1C的中点
∴DF为△ACB1的中位线,∴DF∥AB1,
∵DF?平面BDC1,AB1?平面BDC1,
∴AB1∥平面BDC1;
(2)∵AC∥A1C1,∴∠BAC即为异面直线AB与A1C1所成的角,
∵异面直线AB与A1C1所成的角为30°,∴∠BAC=30°,
∴,
∵D是AC的中点,∴,
又∵CC1⊥平面ABC,CC1=6,E是CC1的中点.
∴.
,
∴.
即三棱锥C1﹣BDE的体积为6.
数学试题 第1*2-1 11页(共12*2 1224页) 数学试题 第1*2 12页(共12*2 1224页)
同课章节目录
