2020-2021年 高中数学人教B版必修四 1.3.2正切函数图象与性质1(共16张PPT)
文档属性
| 名称 | 2020-2021年 高中数学人教B版必修四 1.3.2正切函数图象与性质1(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 562.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 16:28:45 | ||
图片预览





文档简介
(共16张PPT)
1.3.2(2)正切函数的图象和性质
1.
正切函数y=tanx,
(1)定义域:{x∈R|
}
(2)正切函数的周期
所以正切函数的周期是T=π(最小正周期)
(3)正切函数的图象
先做一个周期的图象,我们可选择
的区间作出它的图象。
然后利用正切线画出图象.
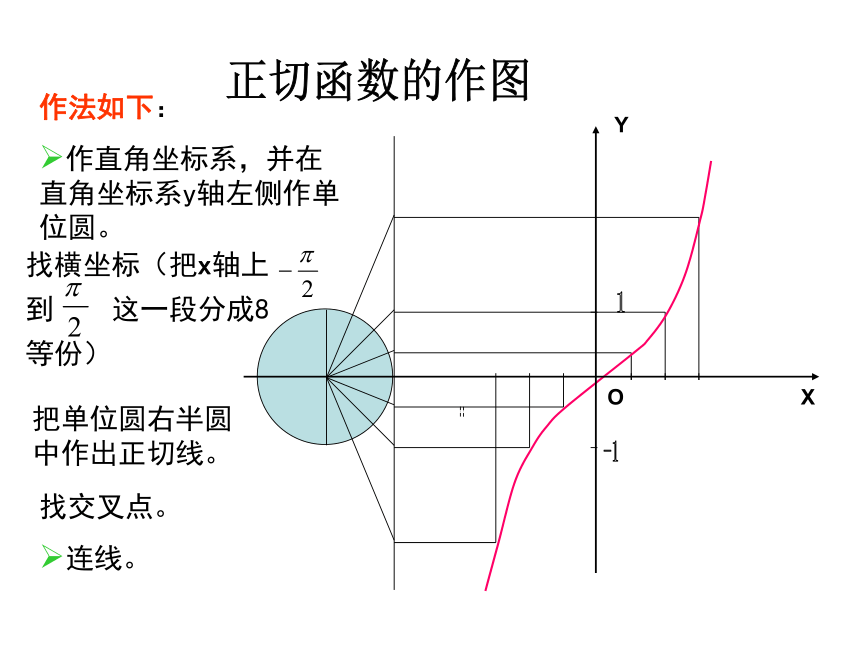
作法如下:
作直角坐标系,并在直角坐标系y轴左侧作单位圆。
X
Y
O
找横坐标(把x轴上 到 这一段分成8等份)
把单位圆右半圆中作出正切线。
找交叉点。
连线。
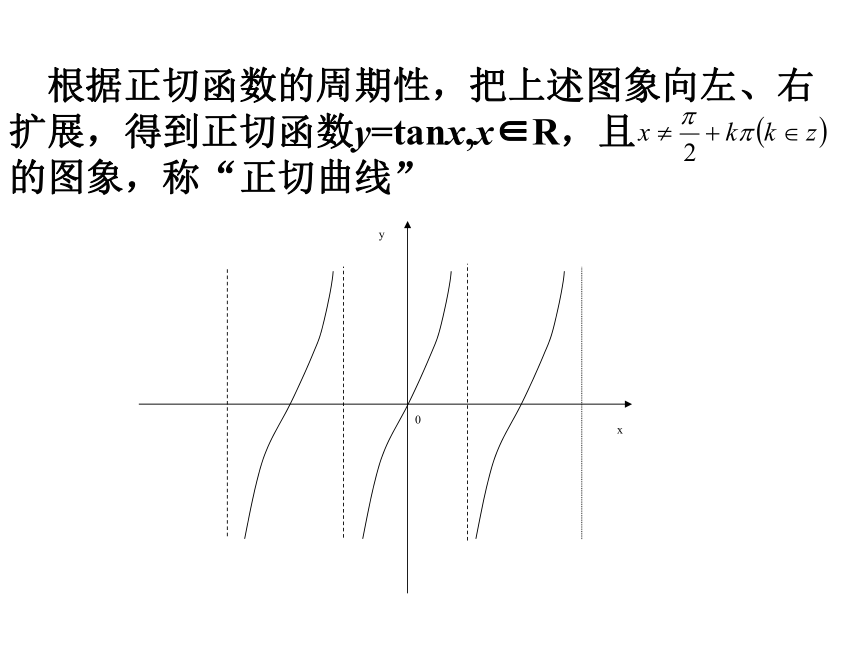
根据正切函数的周期性,把上述图象向左、右扩展,得到正切函数y=tanx,x∈R,且
的图象,称“正切曲线”
0
y
x
2、正切函数的性质
(1)定义域:
;
(2)值域:R
;
观察:当x从小于
,
时,
当x从大于
,
,
。
(3)周期性:T=π;
(4)奇偶性:tan(-x)=-tanx,
∴正切函数是奇函数。
(5)单调性:
在开区间
内,函数单调递增。
例1、比较
与
的大小。
解:
又
内单调递增,
例2 求函数 的定义域。
解:令
那么函数
的定义域是:
所以由 可得:
所以函数 的定义域是:
例3 求下列的单调区间:
例4
求下列函数的周期:
例5.画出函数y=|
tanx|
的图象,指出它的单调区间,奇偶性,周期。
练习:
1.函数y=tan
(2x+
)的周期是
(
)
(A)
π
(B)
2π
(C)
(D)
C
2.已知a=tan1,
b=tan2,
c=tan3,
则a、b、c的大小关系是
(
)
(A)
a(B)
c(C)
b(D)
bC
3.
在下列函数中,同时满足:
(1)
在(0,
)上递增;(2)以2π为周期;(3)是奇函数的是(
)
(A)
y=tan
x
(B)
y=cosx
(C)
y=|tanx|
(D)
y=tan2x
A
4.函数y=lgtan
的定义域是(
)
(A)
{x|kπ,
k∈Z}
(B)
{x|4kπ,
k∈Z}
(C)
{x|2kπk∈Z}
(D)
第一、三象限
C
5.已知函数y=tanωx在(-
,
)内是单调减函数,
则ω的取值范围是
(
)
(A)
0<ω≤
1
(B)
-1≤ω<0
(C)
ω≥1
(D)
ω≤-1
B
1.3.2(2)正切函数的图象和性质
1.
正切函数y=tanx,
(1)定义域:{x∈R|
}
(2)正切函数的周期
所以正切函数的周期是T=π(最小正周期)
(3)正切函数的图象
先做一个周期的图象,我们可选择
的区间作出它的图象。
然后利用正切线画出图象.
作法如下:
作直角坐标系,并在直角坐标系y轴左侧作单位圆。
X
Y
O
找横坐标(把x轴上 到 这一段分成8等份)
把单位圆右半圆中作出正切线。
找交叉点。
连线。
根据正切函数的周期性,把上述图象向左、右扩展,得到正切函数y=tanx,x∈R,且
的图象,称“正切曲线”
0
y
x
2、正切函数的性质
(1)定义域:
;
(2)值域:R
;
观察:当x从小于
,
时,
当x从大于
,
,
。
(3)周期性:T=π;
(4)奇偶性:tan(-x)=-tanx,
∴正切函数是奇函数。
(5)单调性:
在开区间
内,函数单调递增。
例1、比较
与
的大小。
解:
又
内单调递增,
例2 求函数 的定义域。
解:令
那么函数
的定义域是:
所以由 可得:
所以函数 的定义域是:
例3 求下列的单调区间:
例4
求下列函数的周期:
例5.画出函数y=|
tanx|
的图象,指出它的单调区间,奇偶性,周期。
练习:
1.函数y=tan
(2x+
)的周期是
(
)
(A)
π
(B)
2π
(C)
(D)
C
2.已知a=tan1,
b=tan2,
c=tan3,
则a、b、c的大小关系是
(
)
(A)
a
c
b
b
3.
在下列函数中,同时满足:
(1)
在(0,
)上递增;(2)以2π为周期;(3)是奇函数的是(
)
(A)
y=tan
x
(B)
y=cosx
(C)
y=|tanx|
(D)
y=tan2x
A
4.函数y=lgtan
的定义域是(
)
(A)
{x|kπ
k∈Z}
(B)
{x|4kπ
k∈Z}
(C)
{x|2kπ
(D)
第一、三象限
C
5.已知函数y=tanωx在(-
,
)内是单调减函数,
则ω的取值范围是
(
)
(A)
0<ω≤
1
(B)
-1≤ω<0
(C)
ω≥1
(D)
ω≤-1
B
