北师大版七年级下册第四章 三角形 1 认识三角形 课件(23张PPT)
文档属性
| 名称 | 北师大版七年级下册第四章 三角形 1 认识三角形 课件(23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 298.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 08:39:33 | ||
图片预览






文档简介
A
B
C
1.三角形的定义:
由三条不在同一条直线上的线段首尾顺次连结所组成的平面图形叫做三角形;这三条线段就是三角形的三条边。
A
B
C
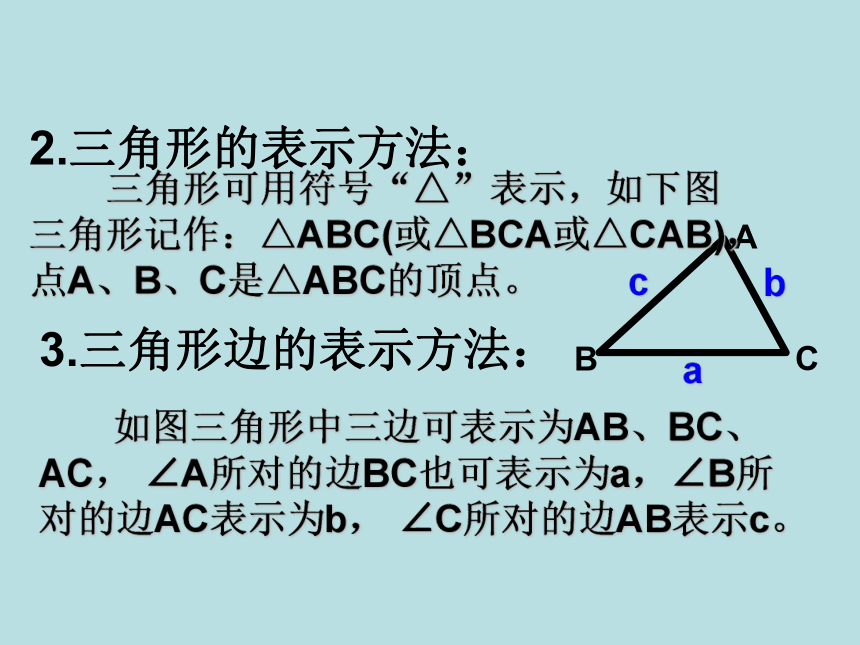
2.三角形的表示方法:
三角形可用符号“△”表示,如下图三角形记作:△ABC(或△BCA或△CAB),点A、B、C是△ABC的顶点。
如图三角形中三边可表示为AB、BC、AC, ∠A所对的边BC也可表示为a,∠B所对的边AC表示为b, ∠C所对的边AB表示c。
3.三角形边的表示方法:
a
b
c
4.三角形的内角:
在三角形中,每两条边所组成的角叫做三角形的内角,简称三角形的角。
如图所示:在△ABC中,三个内角分别为∠A、 ∠ B、 ∠ C.
练习:
1. 图中, △EFH 的内角是______
Q
F
E
P
G
H
练习:
2. 如图,三个三角形的内角各有什么特点?
A
B
C
A
B
C
A
B
C
6.三角形的分类:
① 三角形可以按角来分类:
有一个内角是直角——直角三角形
所有内角都是锐角——锐角三角形
有一个内角是钝角——钝角三角形
其中锐角三角形、钝角三角形统称为斜三角形。
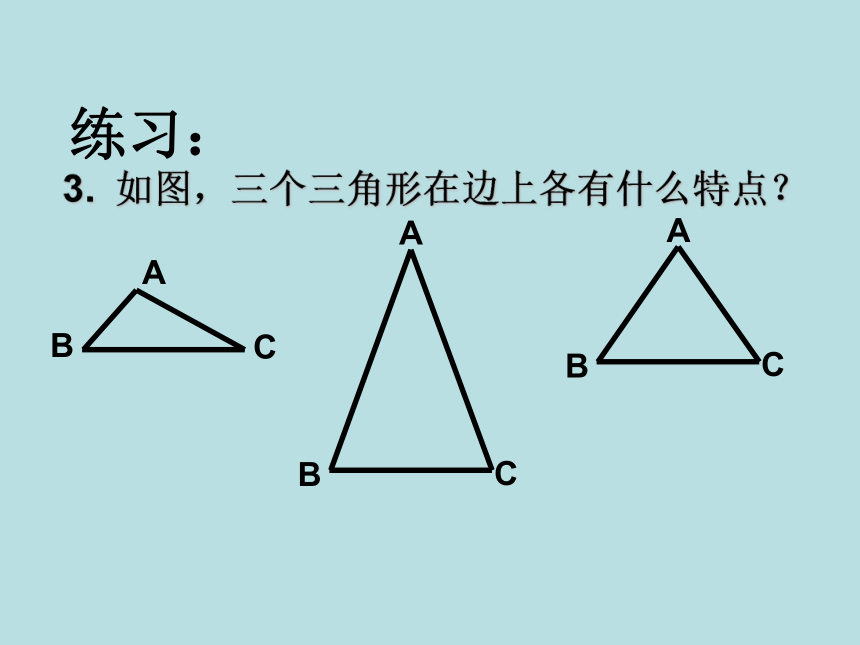
练习:
3. 如图,三个三角形在边上各有什么特点?
A
B
C
A
B
C
A
B
C
6.三角形的分类:
②三角形也可按边来分类:
把两条边相等的三角形称为等腰三角形,相等的两边叫做等腰三角形的腰。
把三条边都相等的三角形称为等边三角形(或正三角形)
把三条边都不相等的三角形称为不等边三角形
例1. 在下面一组图形中:
A
B
C
D
E
A
B
C
D
E
(2)说出各个图形中以B为顶点的角所对的边
(1)每个图中分别有几个三角形?
说出这些三角形;
例2. 画△ABC,在BC边上取三点D、E、F连接AD、AE、AF.
(2)△ADE三边为______三内角为______
B D E F C
A
(4)以AC为边的三角形有______
(1)找出图中所有三角形,用符号表示出来____
(3)以C为顶点的三角形有_______
是否首尾顺次连结的任意三条线段都能组成三角形呢?以下列长度的各组线段为边,能否画一个三角形?试一试.
(3) 7cm,5cm,4cm
(1) 7cm,4cm,2cm
(2) 9cm,5cm,4cm
探索:
三角形的三边关系:
三角形的任意两边之和大于第三边
A
B
C
①AB+BC>AC
②AC+BC>AB
③AB+AC>BC
总结:
练习:
1.判断下列哪几组的线段可以组成三角形.
在判断的过程中,同学们有没有领悟出比较便捷的方法呢?
两条较短的线段和大于较长的线段,那么这三条线段一定可以组成三角形。
9cm, 6cm, 13cm ②18cm, 9cm, 8cm
③2cm, 4cm, 5mm ④ 2a, 3a, 4a(a>0)
思考:
A
B
C
BC>AB-BC
AB>AC-BC
AC>BC-AB
三角形的任意两边之差小于第三边。
①AB+BC>AC→
②AC+BC>AB→
③AB+AC>BC→
三角形的三边关系:
三角形的任意两边之差小于第三边。
三角形的任意两边之和大于第三边
两条性质实质是一样的,体现了三角形的三条边的大小关系,也是判断三条线段是否构成三角形的主要依据。
例题:
2. 一木工有两根长分别为40厘米和60厘米的木条,要另找一根木条,钉成一个三角形木架,第三根木条应在什么范围内?
1. 以四条长度为2、3、4、5的线段中的任意三条为边,可以组成多少个三角形?
结论:
若三角形的两边为a、b,则第三边c的范围是a-b<c<a+b。(a>b)
练习:
1. 已知三角形的三边长为3、5、x,则x的范围是_______
2. 已知三角形的三边长为3、5、2-x,则x的范围是_______
3. 已知三角形两边的长为2和3,则最短边c的取值范围是_______
5. 已知三角形的两边长为4、7,且第三边为偶数,则可以组成____个三角形。
4. 已知三角形的两边长为4、5,则周长c的范围是__________。
练习:
练习:
1. 如果等腰三角形的两边长分别是7cm、8cm,则它的周长是____
2. 如果等腰三角形的两边长分别是4cm、8cm,则它的周长是____
练习:
6. 已知三角形的三边长为2、2m、m+2,则m的范围是_______
7. 已知三角形的三边长为m-2、m、m+2,则m的范围是_______
做一做:
如图所示:在正方形ABCD中,平面内存在一点p,该点与正方形每条边的两个端点的连线所组成的三角形是等腰三角形,这样的p点有多少个?请把它们找出来,并说明理由.
A
B
D
C
1.三角形的概念
2.三角形的三要素
3.三角形的表示方法
4.三角形的分类
本节课的学习你有哪些收获?
B
C
1.三角形的定义:
由三条不在同一条直线上的线段首尾顺次连结所组成的平面图形叫做三角形;这三条线段就是三角形的三条边。
A
B
C
2.三角形的表示方法:
三角形可用符号“△”表示,如下图三角形记作:△ABC(或△BCA或△CAB),点A、B、C是△ABC的顶点。
如图三角形中三边可表示为AB、BC、AC, ∠A所对的边BC也可表示为a,∠B所对的边AC表示为b, ∠C所对的边AB表示c。
3.三角形边的表示方法:
a
b
c
4.三角形的内角:
在三角形中,每两条边所组成的角叫做三角形的内角,简称三角形的角。
如图所示:在△ABC中,三个内角分别为∠A、 ∠ B、 ∠ C.
练习:
1. 图中, △EFH 的内角是______
Q
F
E
P
G
H
练习:
2. 如图,三个三角形的内角各有什么特点?
A
B
C
A
B
C
A
B
C
6.三角形的分类:
① 三角形可以按角来分类:
有一个内角是直角——直角三角形
所有内角都是锐角——锐角三角形
有一个内角是钝角——钝角三角形
其中锐角三角形、钝角三角形统称为斜三角形。
练习:
3. 如图,三个三角形在边上各有什么特点?
A
B
C
A
B
C
A
B
C
6.三角形的分类:
②三角形也可按边来分类:
把两条边相等的三角形称为等腰三角形,相等的两边叫做等腰三角形的腰。
把三条边都相等的三角形称为等边三角形(或正三角形)
把三条边都不相等的三角形称为不等边三角形
例1. 在下面一组图形中:
A
B
C
D
E
A
B
C
D
E
(2)说出各个图形中以B为顶点的角所对的边
(1)每个图中分别有几个三角形?
说出这些三角形;
例2. 画△ABC,在BC边上取三点D、E、F连接AD、AE、AF.
(2)△ADE三边为______三内角为______
B D E F C
A
(4)以AC为边的三角形有______
(1)找出图中所有三角形,用符号表示出来____
(3)以C为顶点的三角形有_______
是否首尾顺次连结的任意三条线段都能组成三角形呢?以下列长度的各组线段为边,能否画一个三角形?试一试.
(3) 7cm,5cm,4cm
(1) 7cm,4cm,2cm
(2) 9cm,5cm,4cm
探索:
三角形的三边关系:
三角形的任意两边之和大于第三边
A
B
C
①AB+BC>AC
②AC+BC>AB
③AB+AC>BC
总结:
练习:
1.判断下列哪几组的线段可以组成三角形.
在判断的过程中,同学们有没有领悟出比较便捷的方法呢?
两条较短的线段和大于较长的线段,那么这三条线段一定可以组成三角形。
9cm, 6cm, 13cm ②18cm, 9cm, 8cm
③2cm, 4cm, 5mm ④ 2a, 3a, 4a(a>0)
思考:
A
B
C
BC>AB-BC
AB>AC-BC
AC>BC-AB
三角形的任意两边之差小于第三边。
①AB+BC>AC→
②AC+BC>AB→
③AB+AC>BC→
三角形的三边关系:
三角形的任意两边之差小于第三边。
三角形的任意两边之和大于第三边
两条性质实质是一样的,体现了三角形的三条边的大小关系,也是判断三条线段是否构成三角形的主要依据。
例题:
2. 一木工有两根长分别为40厘米和60厘米的木条,要另找一根木条,钉成一个三角形木架,第三根木条应在什么范围内?
1. 以四条长度为2、3、4、5的线段中的任意三条为边,可以组成多少个三角形?
结论:
若三角形的两边为a、b,则第三边c的范围是a-b<c<a+b。(a>b)
练习:
1. 已知三角形的三边长为3、5、x,则x的范围是_______
2. 已知三角形的三边长为3、5、2-x,则x的范围是_______
3. 已知三角形两边的长为2和3,则最短边c的取值范围是_______
5. 已知三角形的两边长为4、7,且第三边为偶数,则可以组成____个三角形。
4. 已知三角形的两边长为4、5,则周长c的范围是__________。
练习:
练习:
1. 如果等腰三角形的两边长分别是7cm、8cm,则它的周长是____
2. 如果等腰三角形的两边长分别是4cm、8cm,则它的周长是____
练习:
6. 已知三角形的三边长为2、2m、m+2,则m的范围是_______
7. 已知三角形的三边长为m-2、m、m+2,则m的范围是_______
做一做:
如图所示:在正方形ABCD中,平面内存在一点p,该点与正方形每条边的两个端点的连线所组成的三角形是等腰三角形,这样的p点有多少个?请把它们找出来,并说明理由.
A
B
D
C
1.三角形的概念
2.三角形的三要素
3.三角形的表示方法
4.三角形的分类
本节课的学习你有哪些收获?
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
