北师大版七年级数学下册第四章三角形单元复习课件(共67张ppt)
文档属性
| 名称 | 北师大版七年级数学下册第四章三角形单元复习课件(共67张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-31 22:13:47 | ||
图片预览











文档简介
第四章 三角形
单元复习课
本章知识梳理
目录
02
知识梳理
01
课标要求
课标要求
1. 理解三角形有关概念(内角、外角、中线、高、角平分线),会画出任意三角形的中线、高线和角平分线,了解三角形的稳定性.
2. 掌握三角形的内角和定理(三角形的内角和等于180度),掌握“三角形任意两边之和大于第三边”.
3. 了解全等图形的概念,理解全等三角形的概念,能识别全等三角形的对应边、对应角.
4. 掌握基本事实:三边分别相等的两个三角形全等.
5. 掌握基本事实:两边及其夹角分别相等的两个三角形全等.
6. 掌握基本事实:两角及其夹边分别相等的两个三角形全等.
7. 证明并掌握:两角分别相等且其中一组等角的对边相等的两个三角形全等.
8. 了解等腰三角形的有关概念.
9. 了解等边三角形的概念.
10. 了解直角三角形的概念.
11. 掌握直角三角形的性质定理:直角三角形的两个锐角互余(无需证明).
12. 了解三角形重心的概念.
13. 尺规作图——会利用基本作图作三角形:已知三边作三角形;已知两边及夹角作三角形;已知两角及其夹边作三角形.
知识梳理
{5940675A-B579-460E-94D1-54222C63F5DA}定义
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形
有关线段
中线:在三角形中,连接有关顶点与它对边中点的线段,叫做这个三角形的中线,三角形的三条中线交于一点,这点称为三角形的重心
角平分线:在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线,三角形的三条角平分线交于一点(内心)
高:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高,三角形的三条高所在直线交于一点,交点叫做垂心
{5940675A-B579-460E-94D1-54222C63F5DA}性质
边与边
三角形任意两边之和大于第三边,任意两边之差小于第三边
角与角
三角形的三个内角和等于180°
直角三角形的两个锐角互余
分类
按角分
锐角三角形、直角三角形、钝角三角形
按边分
不等边三角形、等腰三角形、等边三角形
{5940675A-B579-460E-94D1-54222C63F5DA}全等三角形
定义
能够完全重合的两个三角形叫做全等三角形
性质
对应边相等、对应角相等
全等条件
边边边(SSS)、边角边(SAS)、角边角(ASA)、角角边(AAS)
尺规作图
用“SAS”作三角形
用“ASA”作三角形
用“SSS”作三角形
应用
三角形稳定性的应用
用三角形全等测距离
本章易错点归总
易错点
一、判断三条线段能否组成一个三角形,一定要注意任意两边大于第三边才能构成一个三角形,否则就不能组成三角形,其中易出现的错误是只判断有两边之和大于第三边就给予肯定,没有注意任意性而导致解题错误.
【例1】下列长度的三条线段,能组成三角形的是( )
A. 1,2,3 B. 3,4,5
C. 2,4,7 D. 3,5,10
易错提示:解答本题过程中容易忽视三角形判断的任意性,必须是任意的两边之和大于第三边才能构成三角形.
正解:A. 1+2=3,不符合三角形三边关系定理,故本选项错误;B. 3+4>5,3+5>4,4+5>3,符合三角形三边关系定理,故本选项正确;C. 4+2<7,不符合三角形三边关系定理,故本选项错误;D. 5+3<10,不符合三角形三边关系定理,故本选项错误.
答案:B
1. 下列长度的三条线段,可以组成三角形的是( )
A. 10,5,4 B. 3,4,2
C. 1,11,8 D. 5,3,8
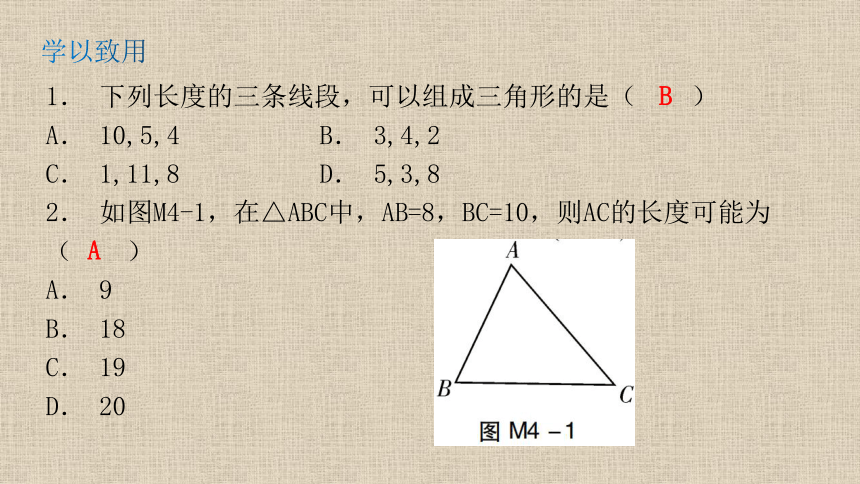
2. 如图M4-1,在△ABC中,AB=8,BC=10,则AC的长度可能为
( )
A. 9
B. 18
C. 19
D. 20
学以致用
B
A
二、在几何图形问题中容易出现通过眼睛观察直接得出全等三角形对应边和对应角相等的错误判断,切记全等三角形对应角所对的边是对应边,对应边所对的角是对应角.
【例2】如图M4-2,△ABC与△DEF是全等三角形,则图中相等的线段的组数是( )
A. 3 B. 4
C. 5 D. 6
易错提示:新生在学习过程中为了求简便直接用眼睛观察而忽视了三角形全等的性质,导致题中出现AB=DF,AC=DE的情况而错误.
正解:因为△ABC≌△DEF,所以AB=DE,AC=DF,BC=EF.所以BC-EC=EF-EC,即BE=CF.所以有四组相等的线段.
答案:B
3. 如图M4-3,已知△ABC≌△CDE,其中AB=CD,那么下列结论中,不正确的是( )
A. AC=CE B. ∠BAC=∠ECD
C. ∠ACB=∠ECD D. ∠B=∠D
C
4. 如图M4-4,全等的三角形是( )
A. Ⅰ和Ⅱ B. Ⅱ和Ⅳ C. Ⅱ和Ⅲ D. Ⅰ和Ⅲ
D
三、SSA是指两个三角形的两边对应相等及一边的对角对应相等,但是这种判断方法是不能判定这两个三角形全等的,SAS是指两个三角形的两条对应边相等且两边的夹角对应相等.
【例3】如图M4-5,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
A. ∠A=∠D B. AB=DC
C. ∠ACB=∠DBC D. AC=BD
易错提示:题中要注意选项D与选项B之间的区别,虽然两个选项给的条件都是两条边及一个角对应相等,但是选项B是以SAS来判定两个三角形全等,而选项D是SSA.
正解:A. 添加∠A=∠D可利用AAS判定△ABC≌△DCB,故此选项不合题意;B. 添加AB=DC可利用SAS定理判定△ABC≌△DCB,故此选项不合题意;C. 添加∠ACB=∠DBC可利用ASA定理判定△ABC≌△DCB,故此选项不合题意;D. 添加AC=BD不能判定△ABC≌△DCB,故此选项符合题意.
答案:D
5. 如图M4-6,下列条件中,不能证明△ABD≌△ACD的是( )
A. BD=CD,AB=AC
B. ∠ADB=∠ADC,BD=CD
C. ∠B=∠C,∠BAD=∠CAD
D. ∠B=∠C,BD=CD
D
6. 如图M4-7,下列各组条件中,不能得到△ABC≌△BAD的是( )
A. BC=AD,∠ABC=∠BAD
B. BC=AD,AC=BD
C. AC=BD,∠CAB=∠DBA
D. BC=AD,∠CAB=∠DBA
D
四、用尺规作图画三角形时,要根据三角形全等的知识来进行判定,只有SSS, ASA, AAS, SAS才能判断作出的三角形跟已知三角形是全等的.
【例4】如图M4-8,请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图.要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是( )
A. 边边边 B. 边角边
C. 角边角 D. 角角边
易错提示:本题是利用圆规来确定OD=O′D′,OC=O′C′,剩下的一个条件在题中表现的不是很明显,学生容易误判为∠O=∠O′而导致错误. 这里最后一个条件是利用直尺来判定CD=C′D′,最后构成SSS的三角形全等.
正解:由作法易得OD=O′D′,OC=O′C′,CD=C′D′,所以△COD≌△C′O′D′(SSS).所以∠DOC=∠D′O′C′.
答案:A
7. 如图M4-9,用尺规作图法作已知角∠AOB的平分线的步骤如下:①以点O为圆心,任意长为半径作弧,交OB于点D,交OA于点E;②分别以点D,E为圆心,以大于DE的长为半径作弧,两弧在∠AOB的内部相交于点C;③作射线OC.则射线OC为∠AOB的平分线.
图M4-9由上述作法可得△OCD≌△OCE的依据是( )
A. SAS B. ASA
C. AAS D. SSS
D
1. 具备下列条件的△ABC中,不是直角三角形的是( )
A. ∠A+∠B=∠C
B. ∠A-∠B=∠C
C. ∠A ∶∠B ∶∠C=1 ∶2 ∶3
D. ∠A=∠B=3∠C
考点1 三角形的概念
D
2. (2020宜昌)能说明命题“锐角α,锐角β的和是锐角”是假命题的例证图是( )
C
3. 如图M4-10,∠1=( )
A. 40°
B. 50°
C. 60°
D. 70°
D
4. 若a,b,c为△ABC的三边长,且满足a-5+(b-3)2=0,则c的值可以为( )
A. 7 B. 8 C. 9 D. 10
5. 若一个三角形的两边长分别为2和4,则该三角形的周长可能是( )
A. 6 B. 7 C. 11 D. 12
A
C
6. 三角形的下列线段中,能将三角形的面积分成相等两部分的是( )
A. 中线 B. 角平分线
C. 高 D. 中位线
7. 三角形三个内角的和等于____________.
A
180°
8. 如图M4-11,北京冬季奥运会吉祥物冰墩墩落在n个三角形内,则n的值为____________.
3
9. 如图M4-12,在△ABC中,AD,BE是两条中线,则S△EDC ∶S△ABC=____________.
1 ∶4
10. 在△ABC中,∠A ∶∠B ∶∠C=2 ∶3 ∶4,则∠A的度数为____________.
11. 等腰三角形两边长分别是3和6,则该三角形的周长为____________.
40°
15
12. 如图M4-13,∠B=∠C,∠ADE=∠AED,∠1=40°,则∠EDC的度数是____________.
20°
13. 如图M4-14,在△ABC中,∠ACB = 60°,∠BAC = 75°,AD⊥BC于点D,BE⊥AC于点E,AD与BE交于点H,求∠CHD的度数.
解:如答图M4-1,延长CH交AB于点F.
因为在△ABC中,三边的高交于一点,所以CF⊥AB.
因为∠ACB=60°,∠BAC=75°,
所以∠ABC=180°-∠ACB-∠BAC=45°.
因为CF⊥AB,所以∠BFC=90°.
所以∠BCF=180°-∠BFC-∠ABC=∠45°.
因为AD⊥BC,所以∠HDC=90°.
所以∠CHD=180°-∠HDC-∠BCF=45°.
14. 已知三角形的三边长分别为a,b,c,其中a,b满足(a-6)2+|b-8|=0,求这个三角形最长边c的取值范围.
解:因为(a-6)2+|b-8|=0,
所以a-6=0,b-8=0.
所以a=6,b=8.
因为b-a<c<a+b且c≥b,
所以8≤c<14.
15. 如图M4-15,在△ABC中,∠B<∠C,AD,AE分别是△ABC的高和角平分线.
(1)若∠B=30°,∠C=50°,则∠DAE的度数是____________;(直接写出答案)
(2)写出∠DAE,∠B,∠C的数量关系:____________________,并说明你的结论.
10°
∠DAE=12(∠C-∠B)
解:(2)因为AD是△ABC的高,所以∠ADC=90°.
所以∠DAC=180°-∠ADC-∠C=90°-∠C.
因为AE是△ABC的角平分线,
所以∠EAC= ∠BAC.因为∠BAC=180°-∠B-∠C,
所以∠DAE=∠EAC-∠DAC= ∠BAC-(90°-∠C)= (180°-∠B-∠C)-90°+∠C=90°- ∠B- ∠C-90°+∠C=
(∠C-∠B).
16. (1)如图M4-16①,△ABC中,BO平分∠ABC,CO平分∠ACB,∠BAC=70°,求∠BOC的度数;
(2)如图M4-16②,若点P为△ABC外部一点,PB平分∠ABC,PC平分外角∠ACD,写出∠BAC和∠BPC的数量关系:
_____________________,并说明你的结论.
∠BPC= ∠BAC
解:(1)因为∠ABO=∠CBO,∠BCO=∠ACO,
所以∠OBC+∠OCB= (∠ABC+∠ACB)= (180°-∠A)=
(180°-70°)=55°.
所以在△BOC中,∠BOC=180°-55°=125°.
(2)易知在△ABC中,∠ACD=∠A+∠ABC,
在△PBC中,∠PCD=∠BPC+∠PBC.
因为PB,PC分别是∠ABC和∠ACD的平分线,
所以∠PCD= ∠ACD,∠PBC= ∠ABC.
所以∠BPC+∠PBC= (∠A+∠ABC)=
∠A+ ∠ABC= ∠A+∠PBC.所以∠BPC= ∠BAC.
1. 如图M4-17:①AB=AD;②∠B=∠D;③∠BAC=∠DAC;④BC=DC. 以上4个等式中的2个等式不能作为依据来说明△ABC≌△ADC的是( )
A. ①② B. ①③
C. ①④ D. ②③
考点2 三角形全等的判定
A
2. 如图M4-18,在Rt△ABC中,∠ACB=90°,BC=4 cm,在AC上取一点E,使EC=BC,过点E作EF⊥AC,连接CF,使CF=AB. 若EF=10 cm,则AE的长为( )
A. 5 cm B. 6 cm
C. 7 cm D. 无法计算
B
3. 给出下列四组条件:
①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E,BC=EF;③∠B=∠E,AC=DF,∠C=∠F;④AB=DE,AC=DF,∠B=∠E.
其中,能使△ABC≌△DEF的条件共有( )
A. 1组 B. 2组 C. 3组 D. 4组
C
4. 下列条件中,不一定能证明两个三角形全等的是( )
A. 两边和一角对应相等
B. 两角和一边对应相等
C. 三边对应相等
D. 两边对应相等的两个直角三角形
A
5. 如图M4-19,已知点E在△ABC的外部,点D在BC边上,DE交AC于点F.若∠1=∠2=∠3,AC=AE,则有( )
A. △ABD≌△AFD
B. △AFE≌△ADC
C. △AEF≌△DFC
D. △ABC≌△ADE
D
6. 如图M4-20,OP平分∠MON,PE⊥OM于点E,PF⊥ON于点F,OA=OB,则图中全等三角形有( )
A. 1对 B. 2对 C. 3对 D. 4对
C
7. 如图M4-21,OP为∠AOB内的一条射线,PC⊥OA,PD⊥OB,垂足分别是C,D,请添加一个条件______________________________,使△COP≌△DOP(填一个即可).
∠COP=∠DOP(答案不唯一)
8. 在如图M4-22所示的3×3正方形网格中,△ABC的顶点都在小正方形的顶点上,像△ABC这样顶点均在格点上的三角形叫做格点三角形.在图中画与△ABC有一条公共边且全等的格点三角形,这样的格点三角形最多可以画 ____________个.
4
9. 如图M4-23,已知正方形ABCD的边长为10 cm,点E在边AB上,且AE=4 cm,如果点P在线段BC上以2 cm/s的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.设运动时间为t s.
(1)若点Q的运动速度与点P的运动速度相等,经过2 s后,△BPE与△CQP是否全等?请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,
则当t为何值时,能够使△BPE与△CQP全等,此时
点Q的运动速度为多少?
解:(1)△BPE与△CQP全等.
因为点Q的运动速度与点P的运动速度相等,且t=2 s,
所以BP=CQ=2×2=4(cm).
因为AB=BC=10 cm,AE=4 cm,所以BE=CP=6 cm.
因为四边形ABCD是正方形,所以∠B=∠C=90°.
在△BPE和△CQP中,
所以△BPE≌△CQP(SAS).
(2)因为点Q的运动速度与点P的运动速度不相等,所以BP≠CQ.
因为∠B=∠C=90°,
所以要使△BPE与△OQP全等,只要BP=PC=5 cm,CQ=BE=6 cm即可.
所以点P,Q运动的时间t=2.5(s).
此时点Q的运动速度为vQ= (cm/s).
10. 如图M4-24,已知DE∥AB,∠DAE=∠B,DE=2,AE=4,C为AE的中点.试说明:△ABC≌△EAD.
解:因为C为AE的中点,AE=4,DE=2,
所以AC= AE=2=DE.
又因为DE∥AB,所以∠BAC=∠E.
在△ABC和△EAD中,∠B=∠DAE,
∠BAC=∠E,AC=DE,
所以△ABC≌△EAD(AAS).
11. 如图M4-25,点D,E分别在AB和AC上,DE∥BC,点F是AD上一点,FE的延长线交BC的延长线CH于点G.
(1)若∠DBE=30°,∠EBC=40°,求∠BDE的度数;
(2)若点E是AC和FG的中点,△AFE与△CEG全等吗?请说明理由.
解:(1)因为DE∥BC,∠EBC=40°,
所以∠DEB=∠EBC=40°.
又因为∠BDE+∠DEB+∠DBE=180°,∠DBE=30°,
所以∠BDE=110°.
(2)全等.
理由:因为E是AC和FG的中点,所以AE=CE,FE=GE.
在△AFE和△CEG中,AE=CE,∠AEF=∠CEG,FE=GE,
所以△AFE≌△CGE(SAS).
12. 已知:AB=AC,BE=CD.
(1)如图M4-26①,试说明:∠B=∠C;
(2)如图M4-26②,连接AO,不添加任何辅助线,写出图中所有的全等三角形,并选一组加以说明.
解:(1)因为AB=AC,BE=CD,
所以AB-BE=AC-CD,即AE=AD.
在△ABD和△ACE中,AD=AE,∠A=∠A,AB=AC,
所以△ABD≌△ACE(SAS).所以∠B=∠C.
(2)图中的全等三角形有△ABD≌△ACE,△AEO≌△ADO,△BEO≌△CDO,△ABO≌△ACO.说明△BEO≌△CDO.
因为在△BEO和△CDO中,∠EOB=∠DOC,∠B=∠C,BE=CD,
所以△BEO≌△CDO(AAS).
1. 某实践活动小组成员要测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再定出BF的垂线DE,使A,C,E在同一条直线上,如图M4-27,可以得到△EDC≌△ABC,所以ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC的理由是( )
A. SAS B. ASA
C. SSS D. AAS
考点3 利用三角形的全等测距离
B
2. 小明用同种材料制成的金属框架如图M4-28,已知∠B=∠E,AB=DE,BF=EC,其中框架三角形ABC的质量为840 g,CF的质量为106 g,则整个金属框架的质量为( )
A. 734 g B. 946 g
C. 1 052 g D. 1 574 g
D
3. 如图M4-29,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线. 此角平分仪的画图原理是根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE,则说明这两个三角形全等的依据是( )
A. SAS B. ASA
C. AAS D. SSS
D
4. 如图M4-30,竖直放置一等腰直角三角板,直角顶点C紧靠在桌面,现量得顶点B到桌面的距离BE=5 cm,CE=12 cm,则顶点A到桌面的距离AD为( )
A. 12 cm
B. 7 cm
C. 17 cm
D. 5 cm
A
5. 如图M4-31,AA′,BB′表示两根长度相同的木条,若O是AA′,BB′的中点,经测量AB=9 cm,则容器的内径A′B′为( )
A. 8 cm
B. 9 cm
C. 10 cm
D. 11 cm
B
6. 在学习完“探索三角形全等的条件”一节后,小丽总结出很多全等三角形的模型,她设计了以下问题给同桌解决:如图M4-32,做一个“U”字形框架PABQ,其中AB=20 cm,AP,BQ足够长,PA⊥AB于点A,QB⊥AB于点B,点M从点B出发向点A运动,点N从点B出发向点Q运动,速度之比为2∶3,运动到某一瞬间两点同时停止.在AP上取点C,使△ACM与△BMN全等,则AC的长度为____________cm.
8或15
7. 如图M4-33,在矩形ABCD中,对角线AC,BD的交点为O,矩形的长、宽分别为7 cm,4 cm,EF过点O分别交AB,DC于点E,F,那么图中阴影部分的面积为____________cm2.
7
8. 如图M4-34,把一块等腰直角三角形零件ABC(∠ACB=90°)放置在一凹槽内,顶点A,B,C分别落在凹槽内壁上,∠ADE=∠BED=90°,测得AD=5 cm,BE=7 cm,则该零件的面积为____________.
37 cm2
9. 如图M4-35,欲计算河中礁石(A点)离岸边B点的距离,请先采用如下方法画图:顺河取一线段BC,在岸上画∠CBE=∠CBA,∠BCF=∠BCA,BE交CF于点D,则BD的长即为A到B的距离(∠CBA,∠BCA的度数可由测角仪量得),然后根据所画图形说明理由.
解:画出图形如答图M4-2.
理由:在△BCD与△BCA中,
∠CBE=∠CBA,BC=BC,
∠BCF=∠BCA,
所以△BCD≌△BCA(ASA).
所以BD=BA.
所以BD的长即为A到B的距离.
10. 某校七年级学生到野外活动,为测量一池塘两端A,B的距离,甲、乙两位同学分别设计出如下两种方案:
甲:如图M4-36①,先在平地取一个可直接到达A,B的点C,再连接AC,BC,并分别延长AC至点D,延长BC至点E,使DC=AC,EC=BC,最后测出DE的长即为A,B的距离.
乙:如图M4-36②,过点B作BD⊥AB,再由点D观测,在AB的延长线上取一点C,使∠BDC=∠BDA,这时只要测出BC的长即为A,B的距离.
(1)以上两位同学所设计的方案,可行的是____________(填“甲”“乙”或“甲和乙”);
(2)请你选择一种可行的方案,说说它可行的理由.
甲和乙
解:(2)答案不唯一.
选甲:在△ABC和△DEC中,AC=DC,∠ACB=∠DCE,EC=BC,
所以△ABC≌△DEC(SAS).所以AB=DE.
选乙:在△ABD和△CBD中,
∠ABD=∠CBD,BD=BD,∠ADB=∠CDB,
所以△ABD≌△CBD(ASA).
所以AB=BC.
单元复习课
本章知识梳理
目录
02
知识梳理
01
课标要求
课标要求
1. 理解三角形有关概念(内角、外角、中线、高、角平分线),会画出任意三角形的中线、高线和角平分线,了解三角形的稳定性.
2. 掌握三角形的内角和定理(三角形的内角和等于180度),掌握“三角形任意两边之和大于第三边”.
3. 了解全等图形的概念,理解全等三角形的概念,能识别全等三角形的对应边、对应角.
4. 掌握基本事实:三边分别相等的两个三角形全等.
5. 掌握基本事实:两边及其夹角分别相等的两个三角形全等.
6. 掌握基本事实:两角及其夹边分别相等的两个三角形全等.
7. 证明并掌握:两角分别相等且其中一组等角的对边相等的两个三角形全等.
8. 了解等腰三角形的有关概念.
9. 了解等边三角形的概念.
10. 了解直角三角形的概念.
11. 掌握直角三角形的性质定理:直角三角形的两个锐角互余(无需证明).
12. 了解三角形重心的概念.
13. 尺规作图——会利用基本作图作三角形:已知三边作三角形;已知两边及夹角作三角形;已知两角及其夹边作三角形.
知识梳理
{5940675A-B579-460E-94D1-54222C63F5DA}定义
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形
有关线段
中线:在三角形中,连接有关顶点与它对边中点的线段,叫做这个三角形的中线,三角形的三条中线交于一点,这点称为三角形的重心
角平分线:在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线,三角形的三条角平分线交于一点(内心)
高:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高,三角形的三条高所在直线交于一点,交点叫做垂心
{5940675A-B579-460E-94D1-54222C63F5DA}性质
边与边
三角形任意两边之和大于第三边,任意两边之差小于第三边
角与角
三角形的三个内角和等于180°
直角三角形的两个锐角互余
分类
按角分
锐角三角形、直角三角形、钝角三角形
按边分
不等边三角形、等腰三角形、等边三角形
{5940675A-B579-460E-94D1-54222C63F5DA}全等三角形
定义
能够完全重合的两个三角形叫做全等三角形
性质
对应边相等、对应角相等
全等条件
边边边(SSS)、边角边(SAS)、角边角(ASA)、角角边(AAS)
尺规作图
用“SAS”作三角形
用“ASA”作三角形
用“SSS”作三角形
应用
三角形稳定性的应用
用三角形全等测距离
本章易错点归总
易错点
一、判断三条线段能否组成一个三角形,一定要注意任意两边大于第三边才能构成一个三角形,否则就不能组成三角形,其中易出现的错误是只判断有两边之和大于第三边就给予肯定,没有注意任意性而导致解题错误.
【例1】下列长度的三条线段,能组成三角形的是( )
A. 1,2,3 B. 3,4,5
C. 2,4,7 D. 3,5,10
易错提示:解答本题过程中容易忽视三角形判断的任意性,必须是任意的两边之和大于第三边才能构成三角形.
正解:A. 1+2=3,不符合三角形三边关系定理,故本选项错误;B. 3+4>5,3+5>4,4+5>3,符合三角形三边关系定理,故本选项正确;C. 4+2<7,不符合三角形三边关系定理,故本选项错误;D. 5+3<10,不符合三角形三边关系定理,故本选项错误.
答案:B
1. 下列长度的三条线段,可以组成三角形的是( )
A. 10,5,4 B. 3,4,2
C. 1,11,8 D. 5,3,8
2. 如图M4-1,在△ABC中,AB=8,BC=10,则AC的长度可能为
( )
A. 9
B. 18
C. 19
D. 20
学以致用
B
A
二、在几何图形问题中容易出现通过眼睛观察直接得出全等三角形对应边和对应角相等的错误判断,切记全等三角形对应角所对的边是对应边,对应边所对的角是对应角.
【例2】如图M4-2,△ABC与△DEF是全等三角形,则图中相等的线段的组数是( )
A. 3 B. 4
C. 5 D. 6
易错提示:新生在学习过程中为了求简便直接用眼睛观察而忽视了三角形全等的性质,导致题中出现AB=DF,AC=DE的情况而错误.
正解:因为△ABC≌△DEF,所以AB=DE,AC=DF,BC=EF.所以BC-EC=EF-EC,即BE=CF.所以有四组相等的线段.
答案:B
3. 如图M4-3,已知△ABC≌△CDE,其中AB=CD,那么下列结论中,不正确的是( )
A. AC=CE B. ∠BAC=∠ECD
C. ∠ACB=∠ECD D. ∠B=∠D
C
4. 如图M4-4,全等的三角形是( )
A. Ⅰ和Ⅱ B. Ⅱ和Ⅳ C. Ⅱ和Ⅲ D. Ⅰ和Ⅲ
D
三、SSA是指两个三角形的两边对应相等及一边的对角对应相等,但是这种判断方法是不能判定这两个三角形全等的,SAS是指两个三角形的两条对应边相等且两边的夹角对应相等.
【例3】如图M4-5,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
A. ∠A=∠D B. AB=DC
C. ∠ACB=∠DBC D. AC=BD
易错提示:题中要注意选项D与选项B之间的区别,虽然两个选项给的条件都是两条边及一个角对应相等,但是选项B是以SAS来判定两个三角形全等,而选项D是SSA.
正解:A. 添加∠A=∠D可利用AAS判定△ABC≌△DCB,故此选项不合题意;B. 添加AB=DC可利用SAS定理判定△ABC≌△DCB,故此选项不合题意;C. 添加∠ACB=∠DBC可利用ASA定理判定△ABC≌△DCB,故此选项不合题意;D. 添加AC=BD不能判定△ABC≌△DCB,故此选项符合题意.
答案:D
5. 如图M4-6,下列条件中,不能证明△ABD≌△ACD的是( )
A. BD=CD,AB=AC
B. ∠ADB=∠ADC,BD=CD
C. ∠B=∠C,∠BAD=∠CAD
D. ∠B=∠C,BD=CD
D
6. 如图M4-7,下列各组条件中,不能得到△ABC≌△BAD的是( )
A. BC=AD,∠ABC=∠BAD
B. BC=AD,AC=BD
C. AC=BD,∠CAB=∠DBA
D. BC=AD,∠CAB=∠DBA
D
四、用尺规作图画三角形时,要根据三角形全等的知识来进行判定,只有SSS, ASA, AAS, SAS才能判断作出的三角形跟已知三角形是全等的.
【例4】如图M4-8,请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图.要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是( )
A. 边边边 B. 边角边
C. 角边角 D. 角角边
易错提示:本题是利用圆规来确定OD=O′D′,OC=O′C′,剩下的一个条件在题中表现的不是很明显,学生容易误判为∠O=∠O′而导致错误. 这里最后一个条件是利用直尺来判定CD=C′D′,最后构成SSS的三角形全等.
正解:由作法易得OD=O′D′,OC=O′C′,CD=C′D′,所以△COD≌△C′O′D′(SSS).所以∠DOC=∠D′O′C′.
答案:A
7. 如图M4-9,用尺规作图法作已知角∠AOB的平分线的步骤如下:①以点O为圆心,任意长为半径作弧,交OB于点D,交OA于点E;②分别以点D,E为圆心,以大于DE的长为半径作弧,两弧在∠AOB的内部相交于点C;③作射线OC.则射线OC为∠AOB的平分线.
图M4-9由上述作法可得△OCD≌△OCE的依据是( )
A. SAS B. ASA
C. AAS D. SSS
D
1. 具备下列条件的△ABC中,不是直角三角形的是( )
A. ∠A+∠B=∠C
B. ∠A-∠B=∠C
C. ∠A ∶∠B ∶∠C=1 ∶2 ∶3
D. ∠A=∠B=3∠C
考点1 三角形的概念
D
2. (2020宜昌)能说明命题“锐角α,锐角β的和是锐角”是假命题的例证图是( )
C
3. 如图M4-10,∠1=( )
A. 40°
B. 50°
C. 60°
D. 70°
D
4. 若a,b,c为△ABC的三边长,且满足a-5+(b-3)2=0,则c的值可以为( )
A. 7 B. 8 C. 9 D. 10
5. 若一个三角形的两边长分别为2和4,则该三角形的周长可能是( )
A. 6 B. 7 C. 11 D. 12
A
C
6. 三角形的下列线段中,能将三角形的面积分成相等两部分的是( )
A. 中线 B. 角平分线
C. 高 D. 中位线
7. 三角形三个内角的和等于____________.
A
180°
8. 如图M4-11,北京冬季奥运会吉祥物冰墩墩落在n个三角形内,则n的值为____________.
3
9. 如图M4-12,在△ABC中,AD,BE是两条中线,则S△EDC ∶S△ABC=____________.
1 ∶4
10. 在△ABC中,∠A ∶∠B ∶∠C=2 ∶3 ∶4,则∠A的度数为____________.
11. 等腰三角形两边长分别是3和6,则该三角形的周长为____________.
40°
15
12. 如图M4-13,∠B=∠C,∠ADE=∠AED,∠1=40°,则∠EDC的度数是____________.
20°
13. 如图M4-14,在△ABC中,∠ACB = 60°,∠BAC = 75°,AD⊥BC于点D,BE⊥AC于点E,AD与BE交于点H,求∠CHD的度数.
解:如答图M4-1,延长CH交AB于点F.
因为在△ABC中,三边的高交于一点,所以CF⊥AB.
因为∠ACB=60°,∠BAC=75°,
所以∠ABC=180°-∠ACB-∠BAC=45°.
因为CF⊥AB,所以∠BFC=90°.
所以∠BCF=180°-∠BFC-∠ABC=∠45°.
因为AD⊥BC,所以∠HDC=90°.
所以∠CHD=180°-∠HDC-∠BCF=45°.
14. 已知三角形的三边长分别为a,b,c,其中a,b满足(a-6)2+|b-8|=0,求这个三角形最长边c的取值范围.
解:因为(a-6)2+|b-8|=0,
所以a-6=0,b-8=0.
所以a=6,b=8.
因为b-a<c<a+b且c≥b,
所以8≤c<14.
15. 如图M4-15,在△ABC中,∠B<∠C,AD,AE分别是△ABC的高和角平分线.
(1)若∠B=30°,∠C=50°,则∠DAE的度数是____________;(直接写出答案)
(2)写出∠DAE,∠B,∠C的数量关系:____________________,并说明你的结论.
10°
∠DAE=12(∠C-∠B)
解:(2)因为AD是△ABC的高,所以∠ADC=90°.
所以∠DAC=180°-∠ADC-∠C=90°-∠C.
因为AE是△ABC的角平分线,
所以∠EAC= ∠BAC.因为∠BAC=180°-∠B-∠C,
所以∠DAE=∠EAC-∠DAC= ∠BAC-(90°-∠C)= (180°-∠B-∠C)-90°+∠C=90°- ∠B- ∠C-90°+∠C=
(∠C-∠B).
16. (1)如图M4-16①,△ABC中,BO平分∠ABC,CO平分∠ACB,∠BAC=70°,求∠BOC的度数;
(2)如图M4-16②,若点P为△ABC外部一点,PB平分∠ABC,PC平分外角∠ACD,写出∠BAC和∠BPC的数量关系:
_____________________,并说明你的结论.
∠BPC= ∠BAC
解:(1)因为∠ABO=∠CBO,∠BCO=∠ACO,
所以∠OBC+∠OCB= (∠ABC+∠ACB)= (180°-∠A)=
(180°-70°)=55°.
所以在△BOC中,∠BOC=180°-55°=125°.
(2)易知在△ABC中,∠ACD=∠A+∠ABC,
在△PBC中,∠PCD=∠BPC+∠PBC.
因为PB,PC分别是∠ABC和∠ACD的平分线,
所以∠PCD= ∠ACD,∠PBC= ∠ABC.
所以∠BPC+∠PBC= (∠A+∠ABC)=
∠A+ ∠ABC= ∠A+∠PBC.所以∠BPC= ∠BAC.
1. 如图M4-17:①AB=AD;②∠B=∠D;③∠BAC=∠DAC;④BC=DC. 以上4个等式中的2个等式不能作为依据来说明△ABC≌△ADC的是( )
A. ①② B. ①③
C. ①④ D. ②③
考点2 三角形全等的判定
A
2. 如图M4-18,在Rt△ABC中,∠ACB=90°,BC=4 cm,在AC上取一点E,使EC=BC,过点E作EF⊥AC,连接CF,使CF=AB. 若EF=10 cm,则AE的长为( )
A. 5 cm B. 6 cm
C. 7 cm D. 无法计算
B
3. 给出下列四组条件:
①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E,BC=EF;③∠B=∠E,AC=DF,∠C=∠F;④AB=DE,AC=DF,∠B=∠E.
其中,能使△ABC≌△DEF的条件共有( )
A. 1组 B. 2组 C. 3组 D. 4组
C
4. 下列条件中,不一定能证明两个三角形全等的是( )
A. 两边和一角对应相等
B. 两角和一边对应相等
C. 三边对应相等
D. 两边对应相等的两个直角三角形
A
5. 如图M4-19,已知点E在△ABC的外部,点D在BC边上,DE交AC于点F.若∠1=∠2=∠3,AC=AE,则有( )
A. △ABD≌△AFD
B. △AFE≌△ADC
C. △AEF≌△DFC
D. △ABC≌△ADE
D
6. 如图M4-20,OP平分∠MON,PE⊥OM于点E,PF⊥ON于点F,OA=OB,则图中全等三角形有( )
A. 1对 B. 2对 C. 3对 D. 4对
C
7. 如图M4-21,OP为∠AOB内的一条射线,PC⊥OA,PD⊥OB,垂足分别是C,D,请添加一个条件______________________________,使△COP≌△DOP(填一个即可).
∠COP=∠DOP(答案不唯一)
8. 在如图M4-22所示的3×3正方形网格中,△ABC的顶点都在小正方形的顶点上,像△ABC这样顶点均在格点上的三角形叫做格点三角形.在图中画与△ABC有一条公共边且全等的格点三角形,这样的格点三角形最多可以画 ____________个.
4
9. 如图M4-23,已知正方形ABCD的边长为10 cm,点E在边AB上,且AE=4 cm,如果点P在线段BC上以2 cm/s的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.设运动时间为t s.
(1)若点Q的运动速度与点P的运动速度相等,经过2 s后,△BPE与△CQP是否全等?请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,
则当t为何值时,能够使△BPE与△CQP全等,此时
点Q的运动速度为多少?
解:(1)△BPE与△CQP全等.
因为点Q的运动速度与点P的运动速度相等,且t=2 s,
所以BP=CQ=2×2=4(cm).
因为AB=BC=10 cm,AE=4 cm,所以BE=CP=6 cm.
因为四边形ABCD是正方形,所以∠B=∠C=90°.
在△BPE和△CQP中,
所以△BPE≌△CQP(SAS).
(2)因为点Q的运动速度与点P的运动速度不相等,所以BP≠CQ.
因为∠B=∠C=90°,
所以要使△BPE与△OQP全等,只要BP=PC=5 cm,CQ=BE=6 cm即可.
所以点P,Q运动的时间t=2.5(s).
此时点Q的运动速度为vQ= (cm/s).
10. 如图M4-24,已知DE∥AB,∠DAE=∠B,DE=2,AE=4,C为AE的中点.试说明:△ABC≌△EAD.
解:因为C为AE的中点,AE=4,DE=2,
所以AC= AE=2=DE.
又因为DE∥AB,所以∠BAC=∠E.
在△ABC和△EAD中,∠B=∠DAE,
∠BAC=∠E,AC=DE,
所以△ABC≌△EAD(AAS).
11. 如图M4-25,点D,E分别在AB和AC上,DE∥BC,点F是AD上一点,FE的延长线交BC的延长线CH于点G.
(1)若∠DBE=30°,∠EBC=40°,求∠BDE的度数;
(2)若点E是AC和FG的中点,△AFE与△CEG全等吗?请说明理由.
解:(1)因为DE∥BC,∠EBC=40°,
所以∠DEB=∠EBC=40°.
又因为∠BDE+∠DEB+∠DBE=180°,∠DBE=30°,
所以∠BDE=110°.
(2)全等.
理由:因为E是AC和FG的中点,所以AE=CE,FE=GE.
在△AFE和△CEG中,AE=CE,∠AEF=∠CEG,FE=GE,
所以△AFE≌△CGE(SAS).
12. 已知:AB=AC,BE=CD.
(1)如图M4-26①,试说明:∠B=∠C;
(2)如图M4-26②,连接AO,不添加任何辅助线,写出图中所有的全等三角形,并选一组加以说明.
解:(1)因为AB=AC,BE=CD,
所以AB-BE=AC-CD,即AE=AD.
在△ABD和△ACE中,AD=AE,∠A=∠A,AB=AC,
所以△ABD≌△ACE(SAS).所以∠B=∠C.
(2)图中的全等三角形有△ABD≌△ACE,△AEO≌△ADO,△BEO≌△CDO,△ABO≌△ACO.说明△BEO≌△CDO.
因为在△BEO和△CDO中,∠EOB=∠DOC,∠B=∠C,BE=CD,
所以△BEO≌△CDO(AAS).
1. 某实践活动小组成员要测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再定出BF的垂线DE,使A,C,E在同一条直线上,如图M4-27,可以得到△EDC≌△ABC,所以ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC的理由是( )
A. SAS B. ASA
C. SSS D. AAS
考点3 利用三角形的全等测距离
B
2. 小明用同种材料制成的金属框架如图M4-28,已知∠B=∠E,AB=DE,BF=EC,其中框架三角形ABC的质量为840 g,CF的质量为106 g,则整个金属框架的质量为( )
A. 734 g B. 946 g
C. 1 052 g D. 1 574 g
D
3. 如图M4-29,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线. 此角平分仪的画图原理是根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE,则说明这两个三角形全等的依据是( )
A. SAS B. ASA
C. AAS D. SSS
D
4. 如图M4-30,竖直放置一等腰直角三角板,直角顶点C紧靠在桌面,现量得顶点B到桌面的距离BE=5 cm,CE=12 cm,则顶点A到桌面的距离AD为( )
A. 12 cm
B. 7 cm
C. 17 cm
D. 5 cm
A
5. 如图M4-31,AA′,BB′表示两根长度相同的木条,若O是AA′,BB′的中点,经测量AB=9 cm,则容器的内径A′B′为( )
A. 8 cm
B. 9 cm
C. 10 cm
D. 11 cm
B
6. 在学习完“探索三角形全等的条件”一节后,小丽总结出很多全等三角形的模型,她设计了以下问题给同桌解决:如图M4-32,做一个“U”字形框架PABQ,其中AB=20 cm,AP,BQ足够长,PA⊥AB于点A,QB⊥AB于点B,点M从点B出发向点A运动,点N从点B出发向点Q运动,速度之比为2∶3,运动到某一瞬间两点同时停止.在AP上取点C,使△ACM与△BMN全等,则AC的长度为____________cm.
8或15
7. 如图M4-33,在矩形ABCD中,对角线AC,BD的交点为O,矩形的长、宽分别为7 cm,4 cm,EF过点O分别交AB,DC于点E,F,那么图中阴影部分的面积为____________cm2.
7
8. 如图M4-34,把一块等腰直角三角形零件ABC(∠ACB=90°)放置在一凹槽内,顶点A,B,C分别落在凹槽内壁上,∠ADE=∠BED=90°,测得AD=5 cm,BE=7 cm,则该零件的面积为____________.
37 cm2
9. 如图M4-35,欲计算河中礁石(A点)离岸边B点的距离,请先采用如下方法画图:顺河取一线段BC,在岸上画∠CBE=∠CBA,∠BCF=∠BCA,BE交CF于点D,则BD的长即为A到B的距离(∠CBA,∠BCA的度数可由测角仪量得),然后根据所画图形说明理由.
解:画出图形如答图M4-2.
理由:在△BCD与△BCA中,
∠CBE=∠CBA,BC=BC,
∠BCF=∠BCA,
所以△BCD≌△BCA(ASA).
所以BD=BA.
所以BD的长即为A到B的距离.
10. 某校七年级学生到野外活动,为测量一池塘两端A,B的距离,甲、乙两位同学分别设计出如下两种方案:
甲:如图M4-36①,先在平地取一个可直接到达A,B的点C,再连接AC,BC,并分别延长AC至点D,延长BC至点E,使DC=AC,EC=BC,最后测出DE的长即为A,B的距离.
乙:如图M4-36②,过点B作BD⊥AB,再由点D观测,在AB的延长线上取一点C,使∠BDC=∠BDA,这时只要测出BC的长即为A,B的距离.
(1)以上两位同学所设计的方案,可行的是____________(填“甲”“乙”或“甲和乙”);
(2)请你选择一种可行的方案,说说它可行的理由.
甲和乙
解:(2)答案不唯一.
选甲:在△ABC和△DEC中,AC=DC,∠ACB=∠DCE,EC=BC,
所以△ABC≌△DEC(SAS).所以AB=DE.
选乙:在△ABD和△CBD中,
∠ABD=∠CBD,BD=BD,∠ADB=∠CDB,
所以△ABD≌△CBD(ASA).
所以AB=BC.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
