9.2.3总体集中趋势的估计 课件(共28张PPT)
文档属性
| 名称 | 9.2.3总体集中趋势的估计 课件(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-01 11:36:58 | ||
图片预览







文档简介
(共28张PPT)
09人教A版
必修二
7.1复数的概念
9.2
用样本估计总体
9.2.3
总体集中趋势的估计
为了了解总体的情况,前面我们研究了如何通过样本的分布规律估计总体的分布规律.但有时候,我们可能不太关心总体的分布规律,而更关注总体取值在某一方面的特征.例如,对于某县今年小麦的收成情况,我们可能会更关注该县今年小麦的总产量或平均每公顷的产量,而不是产量的分布;对于一个国家国民的身高情况,我们可能会更关注身高的平均数或中位数,而不是身高的分布;等等.
在初中的学习中我们已经了解到,平均数、中位数和众数等都是刻画“中心位置”的量,它们从不同角度刻画了一组数据的集中趋势.下面我们通过具体实例进一步了解这些量的意义,探究它们之间的联系与区别,并根据样本的集中趋势估计总体的集中趋势.
例4
利用9.2.1节中100户居民用户的月均用水量的调査数据,计算样本数据的平均数和中位数,并据此估计全市居民用户月均用水量的平均数和中位数.
思考
小明用统计软件计算了100户居民用水量的平均数和中位数.但在录入数据时,不小心把一个数据7.7录成了77.
请计算录入数据的平均数和中位数,并与真实的样本平均数和中位数作比较.
哪个量的值变化更大?你能解释其中的原因吗?
通过简单计算可以发现,平均数由原来的8.79t变为9.483t,中位数没有变化,还是6.6t.这是因为样本平均数与每一个样本数据有关,样本中的任何一个数据的改变都会引起平均数的改变;但中位数只利用了样本数据中间位置的一个或两个值,并未利用其他数据,所以不是任何一个样本数据的改变都会引起中位数的改变.因此,与中位数比较,平均数反映出样本数据中的更多信息,对样本中的极端值更加敏感.
平均数、中位数
(1)
平均数
中位数
(3)
中位数
平均数
(2)
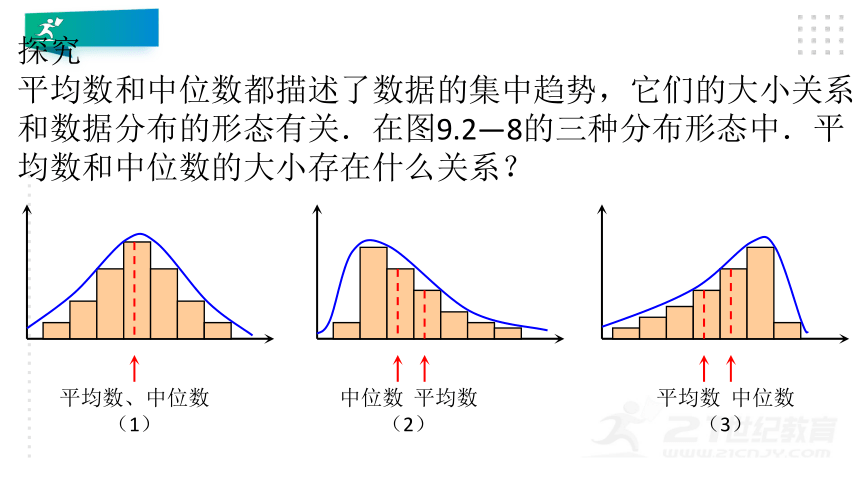
探究
平均数和中位数都描述了数据的集中趋势,它们的大小关系和数据分布的形态有关.在图9.2—8的三种分布形态中.平均数和中位数的大小存在什么关系?
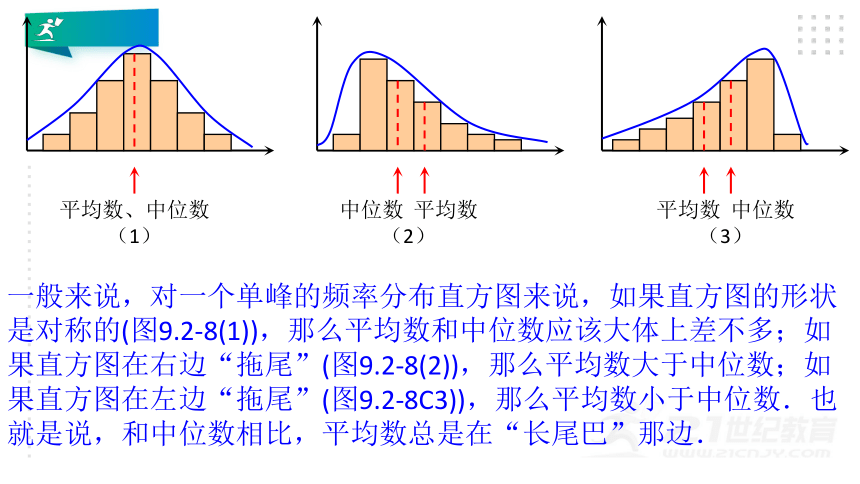
一般来说,对一个单峰的频率分布直方图来说,如果直方图的形状是对称的(图9.2-8(1)),那么平均数和中位数应该大体上差不多;如果直方图在右边“拖尾”(图9.2-8(2)),那么平均数大于中位数;如果直方图在左边“拖尾”(图9.2-8C3)),那么平均数小于中位数.也就是说,和中位数相比,平均数总是在“长尾巴”那边.
平均数、中位数
(1)
平均数
中位数
(3)
中位数
平均数
(2)
例5
某学校要定制高一年级的校服,学生根据厂家提供的参考身高选择校服规格.据统计,高一年级女生需要不同规格校服的频数如表9.2-5所示.
校服规格
155
160
165
170
175
合计
频数
39
64
167
90
26
386
如果用一个量来代表该校高一年级女生所需校服的规格,那么在中位数、平均数和众数中,哪个量比较合适?试讨论用表9.2-5中的数据估计全国高一年级女生校服规格的合理性.
分析:虽然校服规格是用数字表示的,但它们事实上是几种不同的类别.对于这样的分类数据,用众数作为这组数据的代表比较合适.
解:为了更直观地观察数据的特征,我们用条形图来表示表中的数据(图9.2-9).可以发现,选择校服规格为“165”的女生的频数最高,所以用众数165作为该校高一年级女生校服的规格比较合适.
由于全国各地的高一年级女生的身高存在一定的差异,所以用一个学校的数据估计全国高一年级女生的校服规格不合理.
众数只利用了出现次数最多的那个值的信息.众数只能告诉我们它比其他值出现的次数多,但并未告诉我们它比别的数值多的程度.因此,众数只能传递数据中的信息的很少一部分,对极端值也不敏感.
一般地,对数值型数据(如用水量、身高、收入、产量等)集中趋势的描述,可以用平均数、中位数;而对分类型数据(如校服规格、性别、产品质量等级等)集中趋势的描述,可以用众数.
探究
样本的平均数、中位数和众数可以分别作为总体的平均数、中位数和众数的估计,但在某些情况下我们无法获知原始的样本数据.例如,我们在报纸、网络上获得的往往是已经整理好的统计表或统计图.这时该如何估计样本的平均数、中位数和众数?你能以图9.2-1中频率分布直方图提供的信息为例,给出估计方法吗?
在频率分布直方图中,我们无法知道每个组内的数据是如何分布的.此时,通常假设它们在组内均匀分布.这样就可以获得样本的平均数、中位数和众数的近似估计,进而估计总体的平均数、中位数和众数.
因为样本平均数可以表示为数据与它的频率的乘积之和,所以在频率分布直方图中,样本平均数可以用每个小矩形底边中点的横坐标与小矩形的面积的乘积之和近似代替.
这个结果与根据原始数据计算的样本平均数8.79相差不大.
如图9.2-11所示.这个结果与根据原始数据求得的中位数6.6相差不大.
以上我们讨论了平均数、中位数和众数等特征量在刻画一组数据的集中趋势时的各自特点,并研究了用样本的特征量估计总体的特征量的方法.需要注意的是,这些特征量有时也会被利用而产生误导.例如,假设你到人力市场去找工作,有一个企业老板告诉你,“我们企业员工的年平均收入是20万元”,你该如何理解这句话?
这句话是真实的,但它可能描述的是差异巨大的实际情况.例如,可能这个企业的工资水平普遍较高,也就是员工年收入的中位数、众数与平均数差不多;也可能是绝大多数员工的年收入较低(如大多数是5万元左右),而少数员工的年收入很高,甚至达到100万元,在这种情况下年收入的平均数就比中位数大得多.尽管在后一种情况下,用中位数或众数比用平均数更合理些,但这个企业的老板为了招揽员工,却用了平均数.
所以,我们要强调“用数据说话”,但同时又要防止被数据误导,这就需要掌握更多的统计知识和方法.
练习(第208页)
1.根据表9.2-2中的数据,估计该市2015年全年空气质量指数的平均数、中位数和第80百分位数.(注:已知该市属于“严重污染”等级的空气质量指数不超过400).
空气质量等级(空气质量指数AQI)
频数
频率
优(AQI≤50)
83
22.8%
良(50121
33.2%
轻度污染(10068
18.6%
中度污染(15049
13.4%
重度污染(20030
8.2%
严重污染(AQI>300)
14
3.8%
合计
365
100%
2.假设你是某市一名交通部门的工作人员,你打算向市长报告国家对本市26个公路项目投资的平均资金数额.已知国家对本市一条新公路的建设投资为2000万元人民币,对另外25个公路项目的投资是20?100万元,这26个投资金额的中位数是25万元,平均数是100万元,众数是20万元.请你根据上面的信息给市长写一份简要的报告.
为了避免极端值对平均数的影响,可以把新建设公路项目和另外25个公路项目分开报告,例如公路建设的总投资额为2600万元,其中一条新公路的建设投资2000万元,其他25项公路是扩建或部分路段的改造项目,它们的平均投资是
24
万元.
3.某校举行演讲比赛,10位评委对两位选手的评分如下:
甲
7.5
7.5
7.8
7.8
8.0
8.0
8.2
8.3
8.4
9.9
乙
7.5
7.8
7.8
7.8
8.0
8.0
8.3
8.3
8.5
8.5
选手的最终得分为去掉一个最低分和一个最高分之后,剩下8个评分的平均数.那么,这两个选手的最后得分是多少?若直接用10位评委评分的平均数作为选手的得分,两位选手的排名有变化吗?你认为哪种评分办法更好?为什么?
两种评分方法甲、乙得分的平均数见下表:
选手
8位评委评分的平均数
10位评委评分的平均数
甲
8.00
8.14
乙
8.06
8.05
如果采用去掉一个最低分和一个最高分的评分方法,乙选手比甲选手得分高.但是如果按照10
位评委的平均分作为最后的得分,甲选手的得分反而比乙的高.
这是因为有一个评委给甲选手评分为9.9,高出其他评委的评分很多,这一个评委的评分使排名顺序发生了改变.去掉一个最低分和一个最高分的评分机制可以规避个别评委对选手得分的影响.
统计学在军事中的应用——二战时德国坦克总量的估计问题
俗话说,知己知彼方能百战百胜.在第二次世界大战期间,德国制造坦克的技术非常先进,坦克的大量使用使纳粹德国占据了战场主动权.因此,了解德军坦克的生产能力对盟军具有非常重要的战略意义.为此,除了通过常规情报收集信息外,盟军请来了统计学家参与情报的收集和分析工作.根据德国战后公布的生产记录显示,运用统计方法估计的结果与真实值非常接近,而通过常规情报进行的估计则与真实值相去甚远.
下表是二战期间的三个月中,德国记录的生产坦克的数目和情报估计、统计估计的坦克数目.
时间
德国记录/辆
情报估计/辆
统计估计/辆
1940年6月
122
1000
169
1941年6月
271
1550
244
1942年8月
342
1550
327
统计估计有如此高的精确度,统计学家是怎么做到的呢?原来,盟军在缴获的德军坦克上发现了一个重要的线索——每辆坦克上都有一个独一无二的发动机序列号.据分析,序列号前面6位表示生产的年月,最后4位是按生产顺序从1开始的连续编号.统计学家主要是将缴获的德军坦克序列号作为样本,用样本估计总体的方法得出推断的.
0
…
图1
当年,统计学家就是利用上述方法估计德军每月生产的坦克数的.
你还能想出其他估计德军每月生产的坦克数的方法吗?例如,用样本编号的平均数作为每月生产坦克编号的平均数等,比较一下哪种方法更合理.
09人教A版
必修二
7.1复数的概念
9.2
用样本估计总体
9.2.3
总体集中趋势的估计
为了了解总体的情况,前面我们研究了如何通过样本的分布规律估计总体的分布规律.但有时候,我们可能不太关心总体的分布规律,而更关注总体取值在某一方面的特征.例如,对于某县今年小麦的收成情况,我们可能会更关注该县今年小麦的总产量或平均每公顷的产量,而不是产量的分布;对于一个国家国民的身高情况,我们可能会更关注身高的平均数或中位数,而不是身高的分布;等等.
在初中的学习中我们已经了解到,平均数、中位数和众数等都是刻画“中心位置”的量,它们从不同角度刻画了一组数据的集中趋势.下面我们通过具体实例进一步了解这些量的意义,探究它们之间的联系与区别,并根据样本的集中趋势估计总体的集中趋势.
例4
利用9.2.1节中100户居民用户的月均用水量的调査数据,计算样本数据的平均数和中位数,并据此估计全市居民用户月均用水量的平均数和中位数.
思考
小明用统计软件计算了100户居民用水量的平均数和中位数.但在录入数据时,不小心把一个数据7.7录成了77.
请计算录入数据的平均数和中位数,并与真实的样本平均数和中位数作比较.
哪个量的值变化更大?你能解释其中的原因吗?
通过简单计算可以发现,平均数由原来的8.79t变为9.483t,中位数没有变化,还是6.6t.这是因为样本平均数与每一个样本数据有关,样本中的任何一个数据的改变都会引起平均数的改变;但中位数只利用了样本数据中间位置的一个或两个值,并未利用其他数据,所以不是任何一个样本数据的改变都会引起中位数的改变.因此,与中位数比较,平均数反映出样本数据中的更多信息,对样本中的极端值更加敏感.
平均数、中位数
(1)
平均数
中位数
(3)
中位数
平均数
(2)
探究
平均数和中位数都描述了数据的集中趋势,它们的大小关系和数据分布的形态有关.在图9.2—8的三种分布形态中.平均数和中位数的大小存在什么关系?
一般来说,对一个单峰的频率分布直方图来说,如果直方图的形状是对称的(图9.2-8(1)),那么平均数和中位数应该大体上差不多;如果直方图在右边“拖尾”(图9.2-8(2)),那么平均数大于中位数;如果直方图在左边“拖尾”(图9.2-8C3)),那么平均数小于中位数.也就是说,和中位数相比,平均数总是在“长尾巴”那边.
平均数、中位数
(1)
平均数
中位数
(3)
中位数
平均数
(2)
例5
某学校要定制高一年级的校服,学生根据厂家提供的参考身高选择校服规格.据统计,高一年级女生需要不同规格校服的频数如表9.2-5所示.
校服规格
155
160
165
170
175
合计
频数
39
64
167
90
26
386
如果用一个量来代表该校高一年级女生所需校服的规格,那么在中位数、平均数和众数中,哪个量比较合适?试讨论用表9.2-5中的数据估计全国高一年级女生校服规格的合理性.
分析:虽然校服规格是用数字表示的,但它们事实上是几种不同的类别.对于这样的分类数据,用众数作为这组数据的代表比较合适.
解:为了更直观地观察数据的特征,我们用条形图来表示表中的数据(图9.2-9).可以发现,选择校服规格为“165”的女生的频数最高,所以用众数165作为该校高一年级女生校服的规格比较合适.
由于全国各地的高一年级女生的身高存在一定的差异,所以用一个学校的数据估计全国高一年级女生的校服规格不合理.
众数只利用了出现次数最多的那个值的信息.众数只能告诉我们它比其他值出现的次数多,但并未告诉我们它比别的数值多的程度.因此,众数只能传递数据中的信息的很少一部分,对极端值也不敏感.
一般地,对数值型数据(如用水量、身高、收入、产量等)集中趋势的描述,可以用平均数、中位数;而对分类型数据(如校服规格、性别、产品质量等级等)集中趋势的描述,可以用众数.
探究
样本的平均数、中位数和众数可以分别作为总体的平均数、中位数和众数的估计,但在某些情况下我们无法获知原始的样本数据.例如,我们在报纸、网络上获得的往往是已经整理好的统计表或统计图.这时该如何估计样本的平均数、中位数和众数?你能以图9.2-1中频率分布直方图提供的信息为例,给出估计方法吗?
在频率分布直方图中,我们无法知道每个组内的数据是如何分布的.此时,通常假设它们在组内均匀分布.这样就可以获得样本的平均数、中位数和众数的近似估计,进而估计总体的平均数、中位数和众数.
因为样本平均数可以表示为数据与它的频率的乘积之和,所以在频率分布直方图中,样本平均数可以用每个小矩形底边中点的横坐标与小矩形的面积的乘积之和近似代替.
这个结果与根据原始数据计算的样本平均数8.79相差不大.
如图9.2-11所示.这个结果与根据原始数据求得的中位数6.6相差不大.
以上我们讨论了平均数、中位数和众数等特征量在刻画一组数据的集中趋势时的各自特点,并研究了用样本的特征量估计总体的特征量的方法.需要注意的是,这些特征量有时也会被利用而产生误导.例如,假设你到人力市场去找工作,有一个企业老板告诉你,“我们企业员工的年平均收入是20万元”,你该如何理解这句话?
这句话是真实的,但它可能描述的是差异巨大的实际情况.例如,可能这个企业的工资水平普遍较高,也就是员工年收入的中位数、众数与平均数差不多;也可能是绝大多数员工的年收入较低(如大多数是5万元左右),而少数员工的年收入很高,甚至达到100万元,在这种情况下年收入的平均数就比中位数大得多.尽管在后一种情况下,用中位数或众数比用平均数更合理些,但这个企业的老板为了招揽员工,却用了平均数.
所以,我们要强调“用数据说话”,但同时又要防止被数据误导,这就需要掌握更多的统计知识和方法.
练习(第208页)
1.根据表9.2-2中的数据,估计该市2015年全年空气质量指数的平均数、中位数和第80百分位数.(注:已知该市属于“严重污染”等级的空气质量指数不超过400).
空气质量等级(空气质量指数AQI)
频数
频率
优(AQI≤50)
83
22.8%
良(50
33.2%
轻度污染(100
18.6%
中度污染(150
13.4%
重度污染(200
8.2%
严重污染(AQI>300)
14
3.8%
合计
365
100%
2.假设你是某市一名交通部门的工作人员,你打算向市长报告国家对本市26个公路项目投资的平均资金数额.已知国家对本市一条新公路的建设投资为2000万元人民币,对另外25个公路项目的投资是20?100万元,这26个投资金额的中位数是25万元,平均数是100万元,众数是20万元.请你根据上面的信息给市长写一份简要的报告.
为了避免极端值对平均数的影响,可以把新建设公路项目和另外25个公路项目分开报告,例如公路建设的总投资额为2600万元,其中一条新公路的建设投资2000万元,其他25项公路是扩建或部分路段的改造项目,它们的平均投资是
24
万元.
3.某校举行演讲比赛,10位评委对两位选手的评分如下:
甲
7.5
7.5
7.8
7.8
8.0
8.0
8.2
8.3
8.4
9.9
乙
7.5
7.8
7.8
7.8
8.0
8.0
8.3
8.3
8.5
8.5
选手的最终得分为去掉一个最低分和一个最高分之后,剩下8个评分的平均数.那么,这两个选手的最后得分是多少?若直接用10位评委评分的平均数作为选手的得分,两位选手的排名有变化吗?你认为哪种评分办法更好?为什么?
两种评分方法甲、乙得分的平均数见下表:
选手
8位评委评分的平均数
10位评委评分的平均数
甲
8.00
8.14
乙
8.06
8.05
如果采用去掉一个最低分和一个最高分的评分方法,乙选手比甲选手得分高.但是如果按照10
位评委的平均分作为最后的得分,甲选手的得分反而比乙的高.
这是因为有一个评委给甲选手评分为9.9,高出其他评委的评分很多,这一个评委的评分使排名顺序发生了改变.去掉一个最低分和一个最高分的评分机制可以规避个别评委对选手得分的影响.
统计学在军事中的应用——二战时德国坦克总量的估计问题
俗话说,知己知彼方能百战百胜.在第二次世界大战期间,德国制造坦克的技术非常先进,坦克的大量使用使纳粹德国占据了战场主动权.因此,了解德军坦克的生产能力对盟军具有非常重要的战略意义.为此,除了通过常规情报收集信息外,盟军请来了统计学家参与情报的收集和分析工作.根据德国战后公布的生产记录显示,运用统计方法估计的结果与真实值非常接近,而通过常规情报进行的估计则与真实值相去甚远.
下表是二战期间的三个月中,德国记录的生产坦克的数目和情报估计、统计估计的坦克数目.
时间
德国记录/辆
情报估计/辆
统计估计/辆
1940年6月
122
1000
169
1941年6月
271
1550
244
1942年8月
342
1550
327
统计估计有如此高的精确度,统计学家是怎么做到的呢?原来,盟军在缴获的德军坦克上发现了一个重要的线索——每辆坦克上都有一个独一无二的发动机序列号.据分析,序列号前面6位表示生产的年月,最后4位是按生产顺序从1开始的连续编号.统计学家主要是将缴获的德军坦克序列号作为样本,用样本估计总体的方法得出推断的.
0
…
图1
当年,统计学家就是利用上述方法估计德军每月生产的坦克数的.
你还能想出其他估计德军每月生产的坦克数的方法吗?例如,用样本编号的平均数作为每月生产坦克编号的平均数等,比较一下哪种方法更合理.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
