9.2.4总体离散程度的估计 课件(共38张PPT)
文档属性
| 名称 | 9.2.4总体离散程度的估计 课件(共38张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-01 00:00:00 | ||
图片预览











文档简介
(共38张PPT)
09人教A版
必修二
7.1复数的概念
9.2
用样本估计总体
9.2.4
总体离散程度的估计
平均数、中位数和众数为我们提供了一组数据的集中趋势的信息,这是概括一组数据的特征的有效方法.但仅知道集中趋势的信息,很多时候还不能使我们做出有效决策,下面的问题就是一个例子.
问题3
有两位射击运动员在一次射击测试中各射靶10次,每次命中的环数如下:
甲
7
8
7
9
5
4
9
10
7
4
乙
9
5
7
8
7
6
8
6
7
7
如果你是教练,你如何对两位运动员的射击情况作出评价?如果这是一次选拔性考核,你应当如何作出选择?
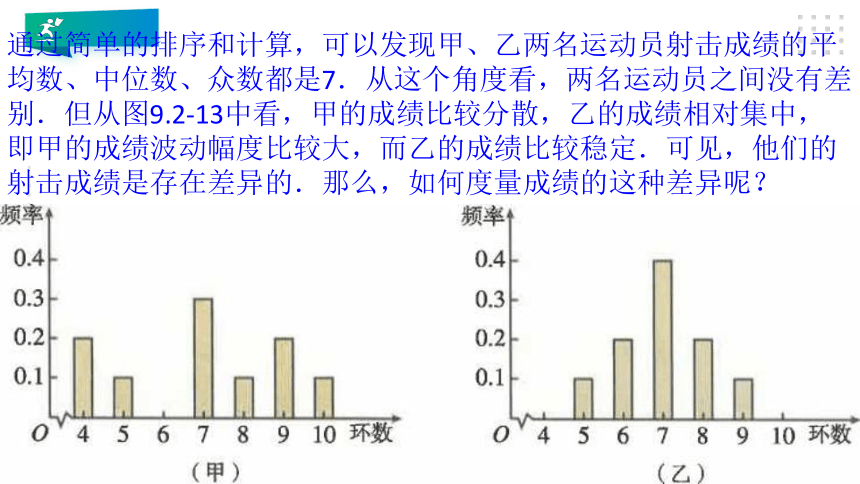
通过简单的排序和计算,可以发现甲、乙两名运动员射击成绩的平均数、中位数、众数都是7.从这个角度看,两名运动员之间没有差别.但从图9.2-13中看,甲的成绩比较分散,乙的成绩相对集中,即甲的成绩波动幅度比较大,而乙的成绩比较稳定.可见,他们的射击成绩是存在差异的.那么,如何度量成绩的这种差异呢?
可以发现甲的成绩波动范围比乙的大.极差在一定程度上刻画了数据的离散程度.但因为极差只使用了数据中最大、最小两个值的信息,对其他数据的取值情况没有涉及,所以极差所含的信息量很少.
我们知道,如果射击的成绩很稳定,那么大多数的射击成绩离平均成绩不会太远;相反,如果射击的成绩波动幅度很大,那么大多数的射击成绩离平均成绩会比较远.因此,我们可以通过这两组射击成绩与它们的平均成绩的“平均距离”来度量成绩的波动幅度.
如何定义“平均距离”?
你还能想出其他刻画数据离散程度的办法吗?
你还能想出其他刻画数据离散程度的办法吗?
标准差的取值范围是什么?标准差为0的一组数据有什么特点?
标准差刻画了数据的离散程度或波动幅度,标准差越大,数据的离散程度越大;标准差越小,数据的离散程度越小.显然,在刻画数据的分散程度上,方差和标准差是一样的.但在解决实际问题中,一般多采用标准差.
在实际问题中,总体平均数和总体标准差都是未知的.就像用样本平均数估计总体平均数一样,通常我们也用样本标准差去估计总体标准差.在随机抽样中,样本标准差依赖于样本的选取,具有随机性.
如果要从这两名选手中选择一名参加比赛,要看一下他们的平均成绩在所有参赛选手中的位置.如果两人都排在前面,就选成绩稳定的乙选手,否则可以选甲.
例6
在对树人中学高一年级学生身高的调查中,采用样本量比例分配的分层随机抽样,如果不知道样本数据,只知道抽取了男生23人,其平均数和方差分别为170.6和12.59,抽取了女生27人,其平均数和方差分别为160.6和38.62.你能由这些数据计算出总样本的方差,并对高一年级全体学生的身高方差作岀估计吗?
我们可以计算出总样本的方差为51.4862,并据此估计高一年级学生身高的总体方差为51.4862.
练习(第213页)
1.不经过计算,你能给下列各组数的方差排序吗?
(1)
5,
5,
5,
5,
5,
5,
5,
5,
5;
(2)
4,
4,
4,
5,
5,
5,
6,
6,
6;
(3)
3,
3,
4,
4,
5,
6,
6,
7,
7;
(4)
2,
2,
2,
2,
5,
8,
8,
8,
8.
3.农场种植的甲、乙两种水稻,在面积相等的两块稻田中连续6年的产量如下:
品种
第1年
第2年
第3年
第4年
第5年
第6年
甲/kg
900
920
900
850
910
920
乙/kg
890
960
950
850
860
890
哪种水稻的产量比较稳定?
甲、乙两种水稻
6
年产量的平均数都是900,但甲种水稻产量的标准差约等于23.8,
乙种水稻产量的标准差约等于41.
6,所以甲种水稻的产量比较稳定.
4.一个小商店从一家有限公司购进21袋白糖,每袋白糖的标准质量是500
g,为了了解这些白糖的质量情况,称出各袋白糖的质量(单位:g)如下:
486
495
496
498
499
493
493
498
484
497
504
489
495
503
499
503
509
498
487
500
508
(1)21袋白糖的平均质量是多少?标准差s是多少?
6.以往的招生统计数据显示,某所大学录取的新生高考总分的中位数基本上稳定在550分.你的一位高中校友在今年的高考中得了520分,你是立即劝阻他报考这所大学,还是先进一步查阅一下这所大学以往招生的其他统计信息?解释一下你的选择.
该高中校友最关心的是自己能否被录取,即他的分数是否在当年录取的最低录取分数之上.根据已有信息,只知道他的分数位于以往分数的中位数之下,这不能判断他被录取的可能性大小.应该进一步查阅这所大学以往招生的其他统计信息,例如以往录取分数的分布情况、平均分数、最低分数等信息.如果知道该校以往录取的平均分数和标准差,且他的分数大于平均分减去标准差的值,那么他被录取的可能性就比较大,可以建议他报考该校;如果知道以往录取分数的分布情况,且他的分数大于第20百分位数,他被录取的可能性也比较大,可以建议他报考该校;如果知道以往录取的最低分数线,且他的分数低于以往最低录取分数线,那么不建议他报考该校;等等.
7.甲、乙两个班级,一次数学考试的分数排序如下:
甲班
51
54
59
60
64
68
68
68
70
71
72
72
74
76
77
78
79
79
80
80
82
85
85
86
86
87
87
87
88
89
90
90
91
96
97
98
98
98
100
100
乙班
61
63
63
66
70
71
71
73
75
75
76
79
79
80
80
80
81
81
82
82
83
83
83
84
84
84
85
85
85
85
85
85
86
87
87
88
90
91
94
98
请你就这次考试成绩,对两个班级的数学学习情况进行评价.
甲班的平均分为80.5,标准差为12.72,最低分为51,最高分为100,极差为49;乙班的平均分为80.5,标准差为8.18,最低分为61,最高分为98,极差为37.
可以发现,甲班和乙班学生的平均分相同,甲班的标准差、极差比乙班的大.这说明甲班学生的成绩比较分散,相互差别较大,数据上看既有成绩不及格的,也有成绩为满分的,相对而言乙班的成绩较为集中,相互差别较小.
8.有一种鱼的身体吸收汞,一定量身体中汞的含量超过其体重的1.00ppm(百万分之一)的鱼被人食用后,就会对人体产生危害.在30条鱼的样本中发现的汞含量(单位:ppm)如下:
0.07
0.24
0.95
0.98
1.02
0.98
1.37
1.40
0.39
1.02
1.44
1.58
0.54
1.08
0.61
0.72
1.20
1.14
1.62
1.68
1.85
1.20
0.81
0.82
0.84
1.29
1.26
2.10
0.91
1.31
(1)请用合适的统计图描述上述数据,并分析这30条鱼的汞含量的分布特点;
(2)求出上述样本数据的平均数和标准差;
(3)从实际情况看,许多鱼的汞含量超标的原因是这些鱼在出售之前没有被检测过.你认为每批这种鱼的平均汞含量都比1.
00
ppm大吗?
(4)在上述样本中,有多少条鱼的汞含量在以平均数为中心、2倍标准差的范围内?
(2)求出上述样本数据的平均数和标准差;
(3)从实际情况看,许多鱼的汞含量超标的原因是这些鱼在出售之前没有被检测过.你认为每批这种鱼的平均汞含量都比1.
00
ppm大吗?
(4)在上述样本中,有多少条鱼的汞含量在以平均数为中心、2倍标准差的范围内?
(4)有
28
条鱼的汞含量在以平均数为中心、2
倍标准差的范围内,占总样本量的
93.
33%.
9.在一次人才招聘会上,有一家公司的招聘员告诉你,“我们公司的收入水平很高”“去年,在
50名员工中,最高年收入达到了200万,员工年收入的平均数是10万”,而你的预期是获得9万元年薪.
(1)你是否能够判断年薪为9万元的员工在这家公司算高收入者?
9.在一次人才招聘会上,有一家公司的招聘员告诉你,“我们公司的收入水平很高”“去年,在
50名员工中,最高年收入达到了200万,员工年收入的平均数是10万”,而你的预期是获得9万元年薪.
(2)如果招聘员继续告诉你,“员工年收入的变化范围是从3万到200万”,这个信息是否足以使你作出自己是否受聘的决定?为什么?
(2)不能.
因为已知有一个极端值,其对均值的影响很大,中位数不受极端值的影响,判断是否受聘还要看中位数的大小,但由“员工年收人的变化范围是从3万到
200万”不能估计中位数的大小.
(3)如果招聘员继续给你提供了如下信息,员工收入的第一四分位数为4.5万,第三四分位数为9.5万,你又该如何使用这条信息来作出是否受聘的决定?
(4)根据(3)中招聘员提供的信息,你能估计出这家公司员工收入的中位数是多少吗?为什么平均数比估计出的中位数高很多?
(3)能.由第一和第三四分位数知,有75%的员工工资在9.5万元以下,其中25%的员工工资在4.5万元以下,所以在该公司获得
9
万元的年薪是有难度的.
(4)由第一和第三四分位数,可以估计中位数在7万元左右.因为有年收入200万这个极端值的影响,得年平均收入比中位数高许多.
10.有20种不同的零食,每100
g可食部分包含的能量(单位:kJ)如下:
110
120
123
165
432
190
174
235
428
318
249
280
162
146
210
120
123
120
150
140
(1)以上述20个数据组成总体,求总体平均数与总体标准差.
(2)设计恰当的随机抽样方法,从总体中抽取一个容量为7的样本,求样本的平均数与标准差.
(1)总体平均数为199.75,总体标准差为95.26.
(2)计算过程略.可以使用抽签法进行抽样。样本平均数和标准差的计算结果和抽取到的样本有关.
10.有20种不同的零食,每100
g可食部分包含的能量(单位:kJ)如下:
110
120
123
165
432
190
174
235
428
318
249
280
162
146
210
120
123
120
150
140
(3)利用上面的抽样方法,再抽取容量为7的样本,计算样本的平均数和标准差.这个样本的平均数和标准差与(2)中的结果一样吗?为什么?
(4)利用(2)中的随机抽样方法,分别从总体中抽取一个容量为10,
13,
16,
19的样本,求样本的平均数与标准差.分析样本容量与样本的平均数和标准差对总体的估计效果之间有什么关系.
(3)计算过程略.不一定一样.因为随机性,每一次所抽取的样本可能不同,所以平均数和标准差可能不同.
(4)计算过程略.一般地,样本量越大对总体的估计越接近,但是由于样本的随机性,也有例外情况.
09人教A版
必修二
7.1复数的概念
9.2
用样本估计总体
9.2.4
总体离散程度的估计
平均数、中位数和众数为我们提供了一组数据的集中趋势的信息,这是概括一组数据的特征的有效方法.但仅知道集中趋势的信息,很多时候还不能使我们做出有效决策,下面的问题就是一个例子.
问题3
有两位射击运动员在一次射击测试中各射靶10次,每次命中的环数如下:
甲
7
8
7
9
5
4
9
10
7
4
乙
9
5
7
8
7
6
8
6
7
7
如果你是教练,你如何对两位运动员的射击情况作出评价?如果这是一次选拔性考核,你应当如何作出选择?
通过简单的排序和计算,可以发现甲、乙两名运动员射击成绩的平均数、中位数、众数都是7.从这个角度看,两名运动员之间没有差别.但从图9.2-13中看,甲的成绩比较分散,乙的成绩相对集中,即甲的成绩波动幅度比较大,而乙的成绩比较稳定.可见,他们的射击成绩是存在差异的.那么,如何度量成绩的这种差异呢?
可以发现甲的成绩波动范围比乙的大.极差在一定程度上刻画了数据的离散程度.但因为极差只使用了数据中最大、最小两个值的信息,对其他数据的取值情况没有涉及,所以极差所含的信息量很少.
我们知道,如果射击的成绩很稳定,那么大多数的射击成绩离平均成绩不会太远;相反,如果射击的成绩波动幅度很大,那么大多数的射击成绩离平均成绩会比较远.因此,我们可以通过这两组射击成绩与它们的平均成绩的“平均距离”来度量成绩的波动幅度.
如何定义“平均距离”?
你还能想出其他刻画数据离散程度的办法吗?
你还能想出其他刻画数据离散程度的办法吗?
标准差的取值范围是什么?标准差为0的一组数据有什么特点?
标准差刻画了数据的离散程度或波动幅度,标准差越大,数据的离散程度越大;标准差越小,数据的离散程度越小.显然,在刻画数据的分散程度上,方差和标准差是一样的.但在解决实际问题中,一般多采用标准差.
在实际问题中,总体平均数和总体标准差都是未知的.就像用样本平均数估计总体平均数一样,通常我们也用样本标准差去估计总体标准差.在随机抽样中,样本标准差依赖于样本的选取,具有随机性.
如果要从这两名选手中选择一名参加比赛,要看一下他们的平均成绩在所有参赛选手中的位置.如果两人都排在前面,就选成绩稳定的乙选手,否则可以选甲.
例6
在对树人中学高一年级学生身高的调查中,采用样本量比例分配的分层随机抽样,如果不知道样本数据,只知道抽取了男生23人,其平均数和方差分别为170.6和12.59,抽取了女生27人,其平均数和方差分别为160.6和38.62.你能由这些数据计算出总样本的方差,并对高一年级全体学生的身高方差作岀估计吗?
我们可以计算出总样本的方差为51.4862,并据此估计高一年级学生身高的总体方差为51.4862.
练习(第213页)
1.不经过计算,你能给下列各组数的方差排序吗?
(1)
5,
5,
5,
5,
5,
5,
5,
5,
5;
(2)
4,
4,
4,
5,
5,
5,
6,
6,
6;
(3)
3,
3,
4,
4,
5,
6,
6,
7,
7;
(4)
2,
2,
2,
2,
5,
8,
8,
8,
8.
3.农场种植的甲、乙两种水稻,在面积相等的两块稻田中连续6年的产量如下:
品种
第1年
第2年
第3年
第4年
第5年
第6年
甲/kg
900
920
900
850
910
920
乙/kg
890
960
950
850
860
890
哪种水稻的产量比较稳定?
甲、乙两种水稻
6
年产量的平均数都是900,但甲种水稻产量的标准差约等于23.8,
乙种水稻产量的标准差约等于41.
6,所以甲种水稻的产量比较稳定.
4.一个小商店从一家有限公司购进21袋白糖,每袋白糖的标准质量是500
g,为了了解这些白糖的质量情况,称出各袋白糖的质量(单位:g)如下:
486
495
496
498
499
493
493
498
484
497
504
489
495
503
499
503
509
498
487
500
508
(1)21袋白糖的平均质量是多少?标准差s是多少?
6.以往的招生统计数据显示,某所大学录取的新生高考总分的中位数基本上稳定在550分.你的一位高中校友在今年的高考中得了520分,你是立即劝阻他报考这所大学,还是先进一步查阅一下这所大学以往招生的其他统计信息?解释一下你的选择.
该高中校友最关心的是自己能否被录取,即他的分数是否在当年录取的最低录取分数之上.根据已有信息,只知道他的分数位于以往分数的中位数之下,这不能判断他被录取的可能性大小.应该进一步查阅这所大学以往招生的其他统计信息,例如以往录取分数的分布情况、平均分数、最低分数等信息.如果知道该校以往录取的平均分数和标准差,且他的分数大于平均分减去标准差的值,那么他被录取的可能性就比较大,可以建议他报考该校;如果知道以往录取分数的分布情况,且他的分数大于第20百分位数,他被录取的可能性也比较大,可以建议他报考该校;如果知道以往录取的最低分数线,且他的分数低于以往最低录取分数线,那么不建议他报考该校;等等.
7.甲、乙两个班级,一次数学考试的分数排序如下:
甲班
51
54
59
60
64
68
68
68
70
71
72
72
74
76
77
78
79
79
80
80
82
85
85
86
86
87
87
87
88
89
90
90
91
96
97
98
98
98
100
100
乙班
61
63
63
66
70
71
71
73
75
75
76
79
79
80
80
80
81
81
82
82
83
83
83
84
84
84
85
85
85
85
85
85
86
87
87
88
90
91
94
98
请你就这次考试成绩,对两个班级的数学学习情况进行评价.
甲班的平均分为80.5,标准差为12.72,最低分为51,最高分为100,极差为49;乙班的平均分为80.5,标准差为8.18,最低分为61,最高分为98,极差为37.
可以发现,甲班和乙班学生的平均分相同,甲班的标准差、极差比乙班的大.这说明甲班学生的成绩比较分散,相互差别较大,数据上看既有成绩不及格的,也有成绩为满分的,相对而言乙班的成绩较为集中,相互差别较小.
8.有一种鱼的身体吸收汞,一定量身体中汞的含量超过其体重的1.00ppm(百万分之一)的鱼被人食用后,就会对人体产生危害.在30条鱼的样本中发现的汞含量(单位:ppm)如下:
0.07
0.24
0.95
0.98
1.02
0.98
1.37
1.40
0.39
1.02
1.44
1.58
0.54
1.08
0.61
0.72
1.20
1.14
1.62
1.68
1.85
1.20
0.81
0.82
0.84
1.29
1.26
2.10
0.91
1.31
(1)请用合适的统计图描述上述数据,并分析这30条鱼的汞含量的分布特点;
(2)求出上述样本数据的平均数和标准差;
(3)从实际情况看,许多鱼的汞含量超标的原因是这些鱼在出售之前没有被检测过.你认为每批这种鱼的平均汞含量都比1.
00
ppm大吗?
(4)在上述样本中,有多少条鱼的汞含量在以平均数为中心、2倍标准差的范围内?
(2)求出上述样本数据的平均数和标准差;
(3)从实际情况看,许多鱼的汞含量超标的原因是这些鱼在出售之前没有被检测过.你认为每批这种鱼的平均汞含量都比1.
00
ppm大吗?
(4)在上述样本中,有多少条鱼的汞含量在以平均数为中心、2倍标准差的范围内?
(4)有
28
条鱼的汞含量在以平均数为中心、2
倍标准差的范围内,占总样本量的
93.
33%.
9.在一次人才招聘会上,有一家公司的招聘员告诉你,“我们公司的收入水平很高”“去年,在
50名员工中,最高年收入达到了200万,员工年收入的平均数是10万”,而你的预期是获得9万元年薪.
(1)你是否能够判断年薪为9万元的员工在这家公司算高收入者?
9.在一次人才招聘会上,有一家公司的招聘员告诉你,“我们公司的收入水平很高”“去年,在
50名员工中,最高年收入达到了200万,员工年收入的平均数是10万”,而你的预期是获得9万元年薪.
(2)如果招聘员继续告诉你,“员工年收入的变化范围是从3万到200万”,这个信息是否足以使你作出自己是否受聘的决定?为什么?
(2)不能.
因为已知有一个极端值,其对均值的影响很大,中位数不受极端值的影响,判断是否受聘还要看中位数的大小,但由“员工年收人的变化范围是从3万到
200万”不能估计中位数的大小.
(3)如果招聘员继续给你提供了如下信息,员工收入的第一四分位数为4.5万,第三四分位数为9.5万,你又该如何使用这条信息来作出是否受聘的决定?
(4)根据(3)中招聘员提供的信息,你能估计出这家公司员工收入的中位数是多少吗?为什么平均数比估计出的中位数高很多?
(3)能.由第一和第三四分位数知,有75%的员工工资在9.5万元以下,其中25%的员工工资在4.5万元以下,所以在该公司获得
9
万元的年薪是有难度的.
(4)由第一和第三四分位数,可以估计中位数在7万元左右.因为有年收入200万这个极端值的影响,得年平均收入比中位数高许多.
10.有20种不同的零食,每100
g可食部分包含的能量(单位:kJ)如下:
110
120
123
165
432
190
174
235
428
318
249
280
162
146
210
120
123
120
150
140
(1)以上述20个数据组成总体,求总体平均数与总体标准差.
(2)设计恰当的随机抽样方法,从总体中抽取一个容量为7的样本,求样本的平均数与标准差.
(1)总体平均数为199.75,总体标准差为95.26.
(2)计算过程略.可以使用抽签法进行抽样。样本平均数和标准差的计算结果和抽取到的样本有关.
10.有20种不同的零食,每100
g可食部分包含的能量(单位:kJ)如下:
110
120
123
165
432
190
174
235
428
318
249
280
162
146
210
120
123
120
150
140
(3)利用上面的抽样方法,再抽取容量为7的样本,计算样本的平均数和标准差.这个样本的平均数和标准差与(2)中的结果一样吗?为什么?
(4)利用(2)中的随机抽样方法,分别从总体中抽取一个容量为10,
13,
16,
19的样本,求样本的平均数与标准差.分析样本容量与样本的平均数和标准差对总体的估计效果之间有什么关系.
(3)计算过程略.不一定一样.因为随机性,每一次所抽取的样本可能不同,所以平均数和标准差可能不同.
(4)计算过程略.一般地,样本量越大对总体的估计越接近,但是由于样本的随机性,也有例外情况.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
