勾股定理
图片预览







文档简介
(共60张PPT)
人教版数学八年级下册
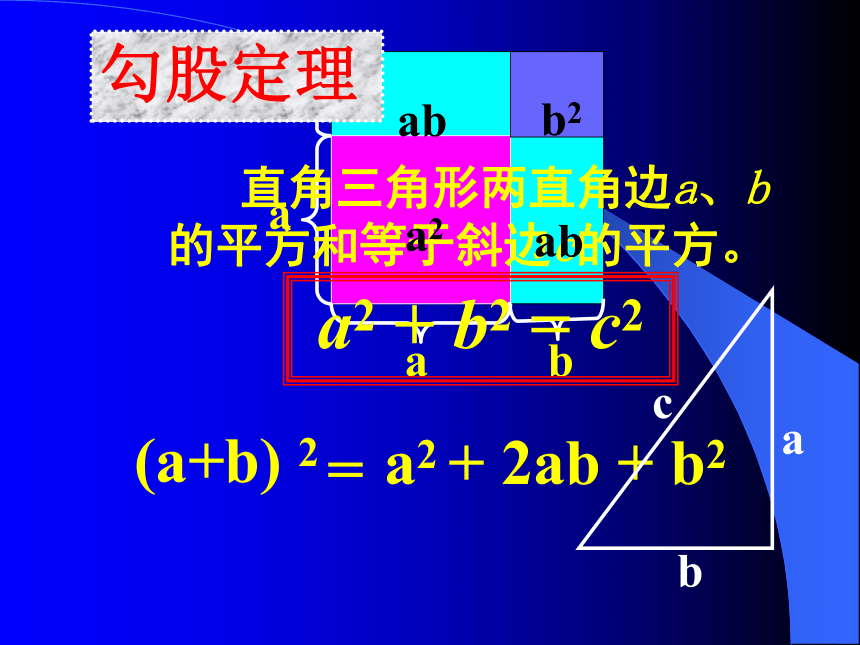
(a+b) 2
b
a
a
b
a2 + 2ab + b2
=
勾股定理
直角三角形两直角边a、b的平方和等于斜边c的平方。
a
b
c
a2 + b2 = c2
ab
ab
a2
b2
验证勾股定理
直角三角形两直角边a、b的平方和等于斜边c的平方。
a2 + b2 = c2
验证勾股定理的方法:
方法 一
方法 二
方法 三
方法 四
方法 五
方法 六
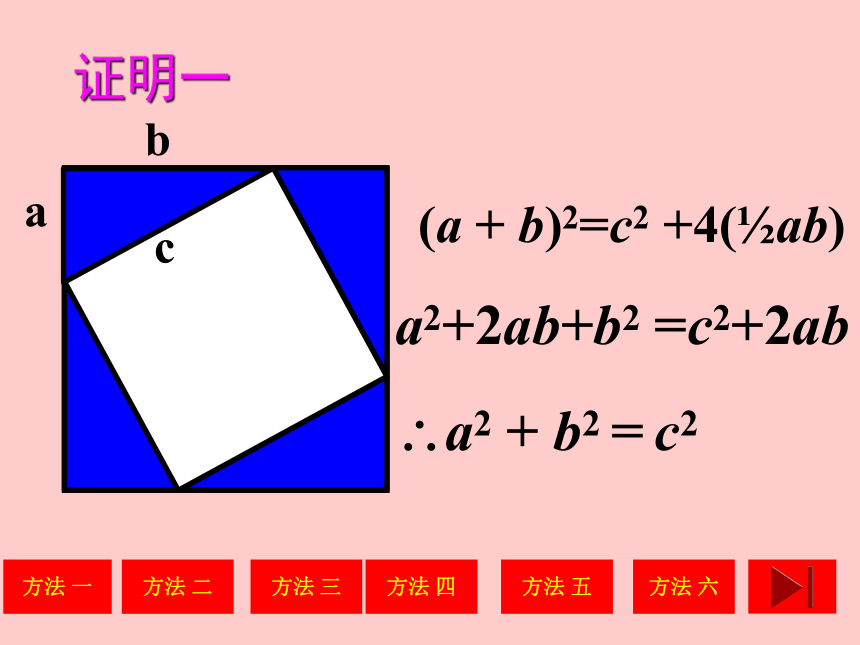
证明一
b
a
(a + b)2 =c2 +4( ab)
a2+2ab+b2 =c2+2ab
a2 + b2 = c2
c
方法 一
方法 二
方法 三
方法 四
方法 五
方法 六
证明二
c
b a
c2= (a b)2+4( ab)
= a2 2ab+b2+2ab
c2 = a2 + b2
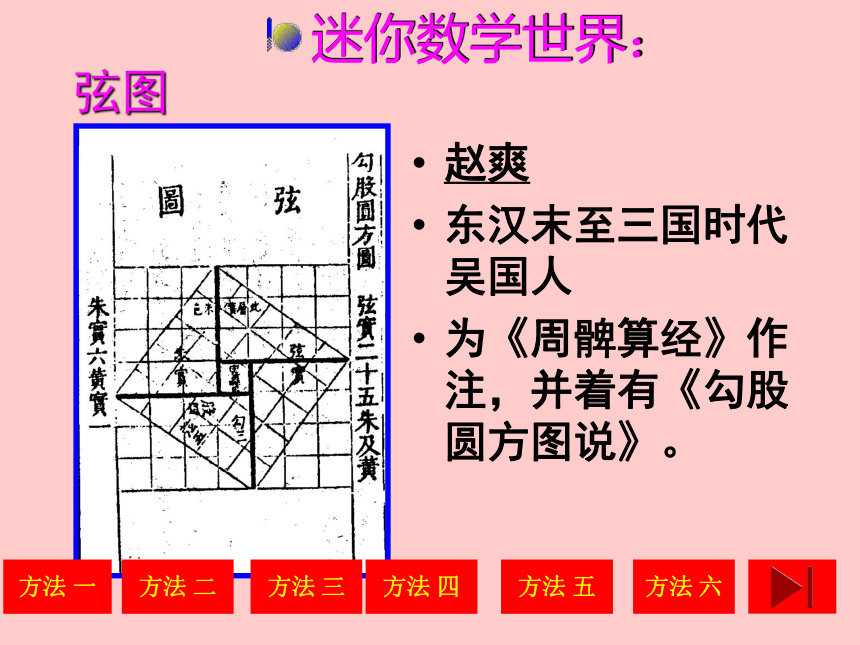
弦图
赵爽
东汉末至三国时代吴国人
为《周髀算经》作注,并着有《勾股圆方图说》。
迷你数学世界:
方法 一
方法 二
方法 三
方法 四
方法 五
方法 六
证明三
(a+b)(b+a)= c2+2( ab)
a2+ab+ b2= c2+ab
a2 + b2 = c2
a
a
b
c
c
美国总统的证明
加菲(James A. Garfield; 1831 1881)
1881 年成为美国第 20 任总统
1876 年提出有关证明
迷你数学世界:
方法 一
方法 二
方法 三
方法 四
方法 五
方法 六
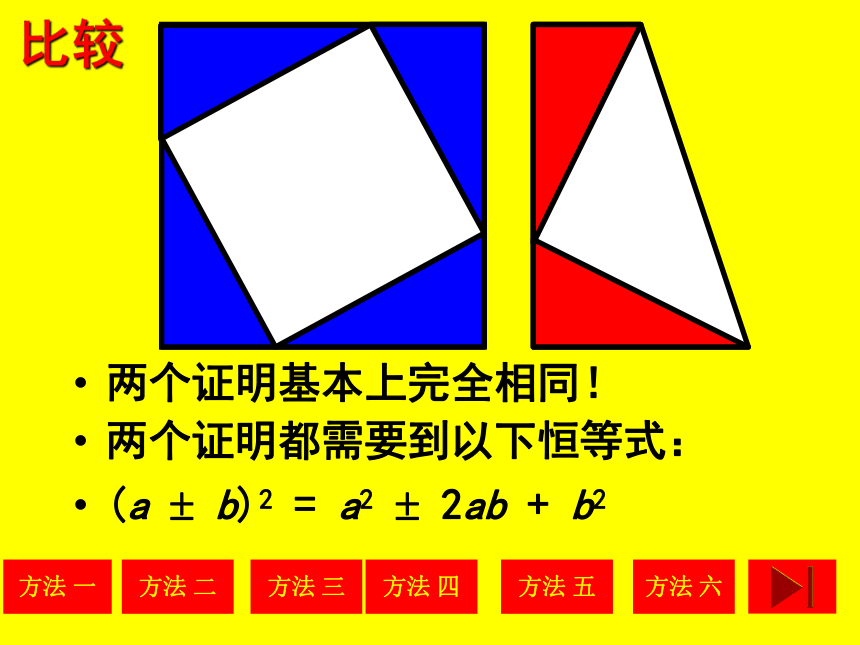
比较
两个证明基本上完全相同!
两个证明都需要到以下恒等式:
(a b)2 = a2 2ab + b2
方法 一
方法 二
方法 三
方法 四
方法 五
方法 六
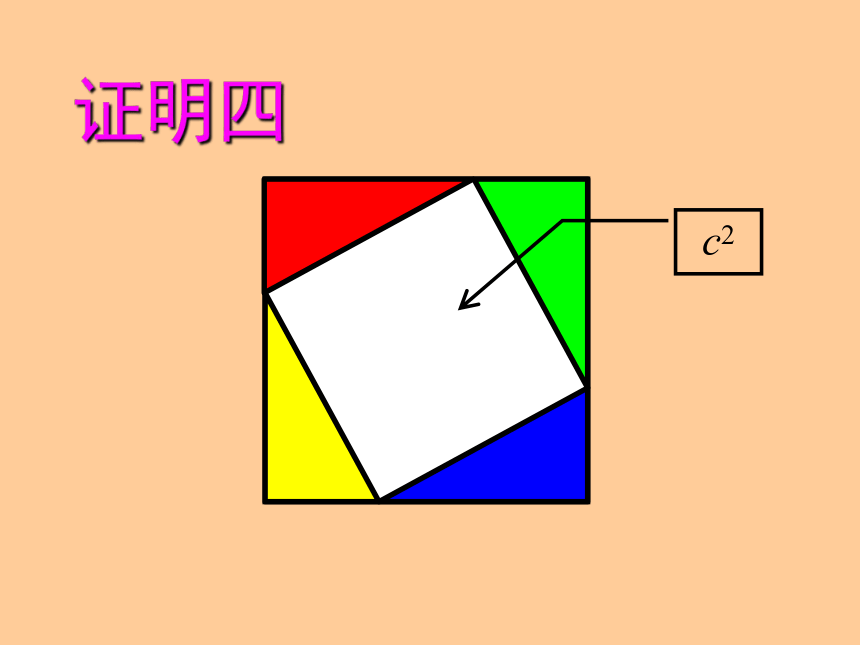
证明四
c2
证明四
证明四
证明四
a2
b2
a2 + b2 = c2
方法 一
方法 二
方法 三
方法 四
方法 五
方法 六
a2
b2
证明五
c2
拼图游戏
证明五
拼图游戏
证明五
拼图游戏
证明五
拼图游戏
c2
a2 + b2 = c2
证明五
拼图游戏
出入相补
刘徽(生於公元三世紀)
三国魏晋时代人。
魏景元四年(即 263 年)为古籍《九章算术》作注释。
在注作中,提出以「出入相补」的原理来证明「勾股定理」。后人称该图为「青朱入出图」。
迷你数学世界:
拼图游戏
方法 一
方法 二
方法 三
方法 四
方法 五
方法 六
证明六
证明六
证明六
证明六
证明六
证明六
证明六
证明六
证明六
证明六
a2 + b2 = c2
几何原本
欧几里得(Euclid of Alexandria; 约 325 B.C. 约 265 B.C.)
欧几里得《几何原本》是用公理方法建立演绎数学体系的最早典范
《几何原本》第一卷的第 47 命題就是上面对勾股定理的证明。
迷你数学世界:
勾股定理
直角三角形两直角边a、b的平方和等于斜边c的平方。
a
b
c
练一练:
1、求出下列直角三角形中未知边的长度。
A
B
C
?
3
4
?
6
8
a b c
3 4 5
15
9
?
6 8 10
9 12 15
练一练:
1、求出下列直角三角形中未知边的长度。
A
B
C
13
?
12
a b c
3 4 5
6 8 10
9 12 15
26
10
?
39
15
?
5 12 13
10 24 26
15 36 39
练一练:
2 .在△ ABC中, ∠C=90°,
(1)若a=5,b=12,则c= _________.
(2)若a=15,c=25,则b= ________.
(3)若c=61,b=60,则a= ________.
(4)若a:b=3:4,c=10,则a= ____,b= ____.
3 .在直角△ ABC中∠C=Rt∠ ,a=5,c=13,则
△ABC的面积 S= _______.
4. 在直角△ ABC中, ∠C=90°,c=20,b=15,则
a=_________.
练一练:
I
II
III
5、面积 I、面积II 与面积III有什么关系?
练一练:
I
II
III
6、面积 I、面积II 与面积III有什么关系?
练一练:
I
II
III
7、面积 I、面积II 与面积III有什么关系?
链接生活
一旗杆离地面6m处折断,旗杆顶部落在离旗杆底部8m处,旗杆折断之前有多高?
6
8
A
B
C
一旗杆离地面6m处折断,旗杆顶部落在离旗杆底部8m处,旗杆折断之前有多高?
链接生活
6
B
A
C
8
A
5000
B
4000
C
审题 → 画示意图→分析题意→解题
你知道吗
飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方4000米处,过了20秒,飞机距离这个男孩头顶5000米。你知道飞机每小时飞行多少千米吗
解:∵△ABC中,∠C=90° ∴ AB =BC +AC (勾股定理) 5000 = BC +4000 , ∴ BC=3000
∴ 3000÷20×60×60 =540000米 =540千米
答:飞机每小时飞行540千米。
A
C
B
4000
5000
你知道吗
某楼房三楼失火,消防队员赶来救火,了解到每层楼高3米,消防队员取来6.5米长的云梯,如果梯子的底部离墙基的距离是2.5米,请问消防队员能否进入三楼灭火
紧急求助:
某楼房三楼失火,消防队员赶来救火,了解到每层楼高3米,消防队员取来6.5米长的云梯,如果梯子的底部离墙基的距离是2.5米,请问消防队员能否进入三楼灭火
紧急求助:
审题→画示意图→分析题意→解题
A
C
B
解:由勾股定理知
AB =BC +AC , 即 AB =6 +2.5 ,
AB=6.5
所以消防队员能进入三楼灭火。
能力提升平台:
如图,一个2.5m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗
若不是,将外移多少?
能力提升平台:
如图,一个2.5m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗
若不是,将外移多少?
能力提升平台:
A
C
B
D
O
0.5
如图,一个2.5m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗
若不是,将外移多少?
如图,一个2.5m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.4m,如果梯子的顶端A沿墙下滑0.4m,那么梯子底端B也外移0.4m吗
若不是,将外移多少?
能力提升平台:
A
C
B
D
O
0.4
在平静的湖面上,有一支红莲,高出水面1米,一阵风吹来,红莲被吹到一边,花朵齐及水面,已知红莲移动的水平距离为2米,问此时水深为多少?
智慧宫:
笨人持竿要进屋,无奈门框拦住竹,横多四尺竖多二,没法急得放声哭,有个邻居聪明者,教他斜竿对角入,笨伯依言试一试,不多不少刚抵足,借问竿长多少数,谁人算出我佩服。
学科渗透:
-----当代数学教育家清华大学教授
许莼舫著作《古算题味》
一辆装满货物的卡车,要开进某工厂(如图所示)。
探究实践:
一辆装满货物的卡车,高2.5米,宽1.6米,要开进某工厂(厂门如图所示),
问这辆卡车
能否通过厂门?
说明你的理由。
2.3米
2米
探究实践:
A
B
C
D
E
F
O
P
聪明的蚂蚁
一个长,宽,高分别为15厘米,10厘米,20厘米的木箱,一只聪明蚂蚁如果沿着它的表面从A点爬到B点。
聪明的蚂蚁沿哪条 路线爬最近? 你能帮它找出来吗?
A
B
.
.
谈收获
课后探索
做一个长,宽,高分别为50厘米,40厘米,30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明。
课后作业:
78页4、5题
再见
人教版数学八年级下册
(a+b) 2
b
a
a
b
a2 + 2ab + b2
=
勾股定理
直角三角形两直角边a、b的平方和等于斜边c的平方。
a
b
c
a2 + b2 = c2
ab
ab
a2
b2
验证勾股定理
直角三角形两直角边a、b的平方和等于斜边c的平方。
a2 + b2 = c2
验证勾股定理的方法:
方法 一
方法 二
方法 三
方法 四
方法 五
方法 六
证明一
b
a
(a + b)2 =c2 +4( ab)
a2+2ab+b2 =c2+2ab
a2 + b2 = c2
c
方法 一
方法 二
方法 三
方法 四
方法 五
方法 六
证明二
c
b a
c2= (a b)2+4( ab)
= a2 2ab+b2+2ab
c2 = a2 + b2
弦图
赵爽
东汉末至三国时代吴国人
为《周髀算经》作注,并着有《勾股圆方图说》。
迷你数学世界:
方法 一
方法 二
方法 三
方法 四
方法 五
方法 六
证明三
(a+b)(b+a)= c2+2( ab)
a2+ab+ b2= c2+ab
a2 + b2 = c2
a
a
b
c
c
美国总统的证明
加菲(James A. Garfield; 1831 1881)
1881 年成为美国第 20 任总统
1876 年提出有关证明
迷你数学世界:
方法 一
方法 二
方法 三
方法 四
方法 五
方法 六
比较
两个证明基本上完全相同!
两个证明都需要到以下恒等式:
(a b)2 = a2 2ab + b2
方法 一
方法 二
方法 三
方法 四
方法 五
方法 六
证明四
c2
证明四
证明四
证明四
a2
b2
a2 + b2 = c2
方法 一
方法 二
方法 三
方法 四
方法 五
方法 六
a2
b2
证明五
c2
拼图游戏
证明五
拼图游戏
证明五
拼图游戏
证明五
拼图游戏
c2
a2 + b2 = c2
证明五
拼图游戏
出入相补
刘徽(生於公元三世紀)
三国魏晋时代人。
魏景元四年(即 263 年)为古籍《九章算术》作注释。
在注作中,提出以「出入相补」的原理来证明「勾股定理」。后人称该图为「青朱入出图」。
迷你数学世界:
拼图游戏
方法 一
方法 二
方法 三
方法 四
方法 五
方法 六
证明六
证明六
证明六
证明六
证明六
证明六
证明六
证明六
证明六
证明六
a2 + b2 = c2
几何原本
欧几里得(Euclid of Alexandria; 约 325 B.C. 约 265 B.C.)
欧几里得《几何原本》是用公理方法建立演绎数学体系的最早典范
《几何原本》第一卷的第 47 命題就是上面对勾股定理的证明。
迷你数学世界:
勾股定理
直角三角形两直角边a、b的平方和等于斜边c的平方。
a
b
c
练一练:
1、求出下列直角三角形中未知边的长度。
A
B
C
?
3
4
?
6
8
a b c
3 4 5
15
9
?
6 8 10
9 12 15
练一练:
1、求出下列直角三角形中未知边的长度。
A
B
C
13
?
12
a b c
3 4 5
6 8 10
9 12 15
26
10
?
39
15
?
5 12 13
10 24 26
15 36 39
练一练:
2 .在△ ABC中, ∠C=90°,
(1)若a=5,b=12,则c= _________.
(2)若a=15,c=25,则b= ________.
(3)若c=61,b=60,则a= ________.
(4)若a:b=3:4,c=10,则a= ____,b= ____.
3 .在直角△ ABC中∠C=Rt∠ ,a=5,c=13,则
△ABC的面积 S= _______.
4. 在直角△ ABC中, ∠C=90°,c=20,b=15,则
a=_________.
练一练:
I
II
III
5、面积 I、面积II 与面积III有什么关系?
练一练:
I
II
III
6、面积 I、面积II 与面积III有什么关系?
练一练:
I
II
III
7、面积 I、面积II 与面积III有什么关系?
链接生活
一旗杆离地面6m处折断,旗杆顶部落在离旗杆底部8m处,旗杆折断之前有多高?
6
8
A
B
C
一旗杆离地面6m处折断,旗杆顶部落在离旗杆底部8m处,旗杆折断之前有多高?
链接生活
6
B
A
C
8
A
5000
B
4000
C
审题 → 画示意图→分析题意→解题
你知道吗
飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方4000米处,过了20秒,飞机距离这个男孩头顶5000米。你知道飞机每小时飞行多少千米吗
解:∵△ABC中,∠C=90° ∴ AB =BC +AC (勾股定理) 5000 = BC +4000 , ∴ BC=3000
∴ 3000÷20×60×60 =540000米 =540千米
答:飞机每小时飞行540千米。
A
C
B
4000
5000
你知道吗
某楼房三楼失火,消防队员赶来救火,了解到每层楼高3米,消防队员取来6.5米长的云梯,如果梯子的底部离墙基的距离是2.5米,请问消防队员能否进入三楼灭火
紧急求助:
某楼房三楼失火,消防队员赶来救火,了解到每层楼高3米,消防队员取来6.5米长的云梯,如果梯子的底部离墙基的距离是2.5米,请问消防队员能否进入三楼灭火
紧急求助:
审题→画示意图→分析题意→解题
A
C
B
解:由勾股定理知
AB =BC +AC , 即 AB =6 +2.5 ,
AB=6.5
所以消防队员能进入三楼灭火。
能力提升平台:
如图,一个2.5m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗
若不是,将外移多少?
能力提升平台:
如图,一个2.5m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗
若不是,将外移多少?
能力提升平台:
A
C
B
D
O
0.5
如图,一个2.5m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗
若不是,将外移多少?
如图,一个2.5m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.4m,如果梯子的顶端A沿墙下滑0.4m,那么梯子底端B也外移0.4m吗
若不是,将外移多少?
能力提升平台:
A
C
B
D
O
0.4
在平静的湖面上,有一支红莲,高出水面1米,一阵风吹来,红莲被吹到一边,花朵齐及水面,已知红莲移动的水平距离为2米,问此时水深为多少?
智慧宫:
笨人持竿要进屋,无奈门框拦住竹,横多四尺竖多二,没法急得放声哭,有个邻居聪明者,教他斜竿对角入,笨伯依言试一试,不多不少刚抵足,借问竿长多少数,谁人算出我佩服。
学科渗透:
-----当代数学教育家清华大学教授
许莼舫著作《古算题味》
一辆装满货物的卡车,要开进某工厂(如图所示)。
探究实践:
一辆装满货物的卡车,高2.5米,宽1.6米,要开进某工厂(厂门如图所示),
问这辆卡车
能否通过厂门?
说明你的理由。
2.3米
2米
探究实践:
A
B
C
D
E
F
O
P
聪明的蚂蚁
一个长,宽,高分别为15厘米,10厘米,20厘米的木箱,一只聪明蚂蚁如果沿着它的表面从A点爬到B点。
聪明的蚂蚁沿哪条 路线爬最近? 你能帮它找出来吗?
A
B
.
.
谈收获
课后探索
做一个长,宽,高分别为50厘米,40厘米,30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明。
课后作业:
78页4、5题
再见
