2020-2021学年人教五四新版八年级下册数学期末练习试题(Word版有答案)
文档属性
| 名称 | 2020-2021学年人教五四新版八年级下册数学期末练习试题(Word版有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 403.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-01 07:58:38 | ||
图片预览



文档简介
2020-2021学年人教五四新版八年级下册数学期末练习试题
一.选择题(共10小题,满分30分,每小题3分)
1.下列方程一定是一元二次方程的是( )
A.3x2+﹣1=0
B.5x2﹣6y﹣3=0
C.ax2﹣x+2=0
D.3x2﹣2x﹣1=0
2.下列各组数中,能构成直角三角形的是( )
A.4,5,6
B.1,1,
C.6,8,11
D.5,12,23
3.若直线y=kx+b经过一、二、四象限,则直线y=bx﹣k的图象只能是图中的( )
A.
B.
C.
D.
4.下列四个命题中,真命题有( )
①两条直线被第三条直线所截,内错角相等.
②如果∠1和∠2是对顶角,那么∠1=∠2.
③三角形的一个外角大于任何一个内角.
④如果x2>0,那么x>0.
A.1个
B.2个
C.3个
D.4个
5.如图:将一个矩形纸片ABCD,沿着BE折叠,使C、D点分别落在点C1,D1处.若∠C1BA=50°,则∠ABE的度数为( )
A.15°
B.20°
C.25°
D.30°
6.下列四组线段中,可以构成直角三角形的是( )
A.1.5,2,2.5
B.4,5,6
C.2,3,4
D.1,,3
7.已知关于x的一元二次方程x2﹣(2m﹣1)x+m2=0有实数根,则m的取值范围是( )
A.m≠0
B.m≤
C.m<
D.m>
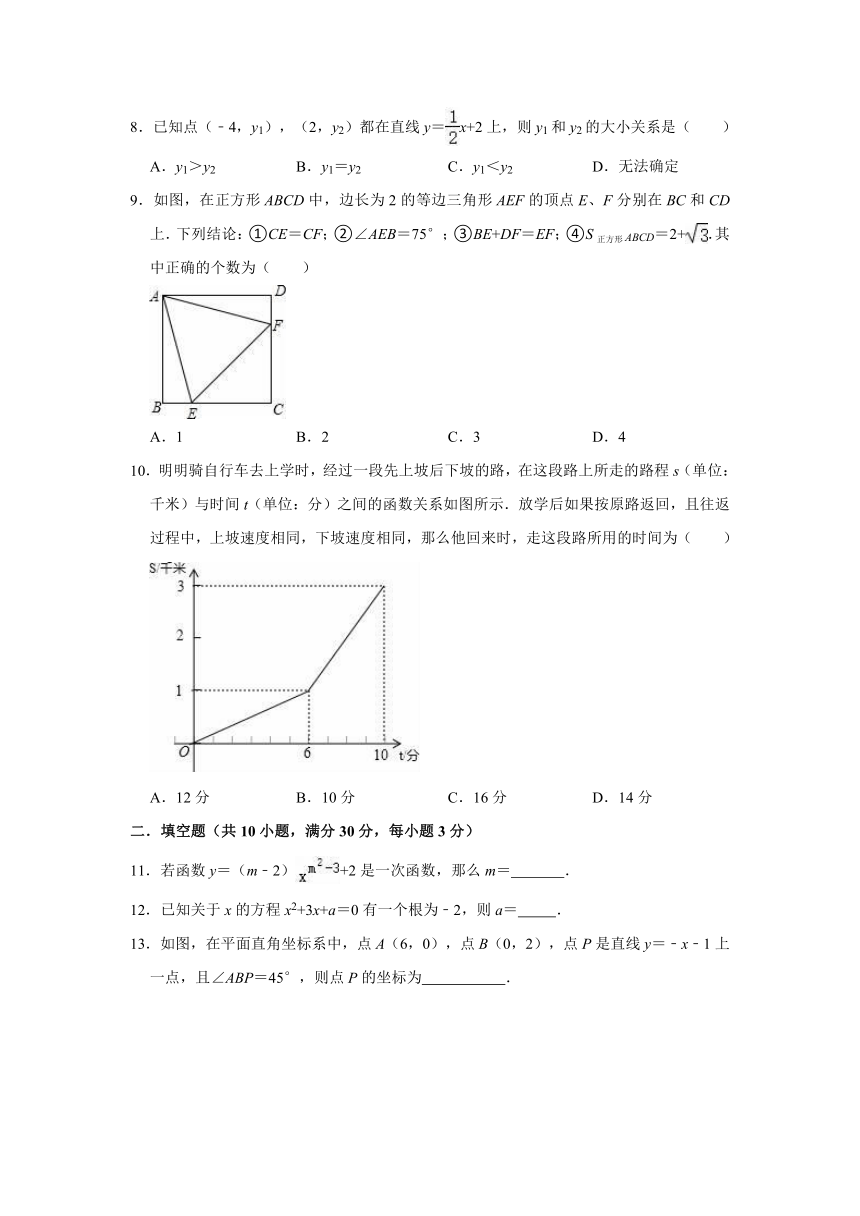
8.已知点(﹣4,y1),(2,y2)都在直线y=x+2上,则y1和y2的大小关系是( )
A.y1>y2
B.y1=y2
C.y1<y2
D.无法确定
9.如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上.下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+.其中正确的个数为( )
A.1
B.2
C.3
D.4
10.明明骑自行车去上学时,经过一段先上坡后下坡的路,在这段路上所走的路程s(单位:千米)与时间t(单位:分)之间的函数关系如图所示.放学后如果按原路返回,且往返过程中,上坡速度相同,下坡速度相同,那么他回来时,走这段路所用的时间为( )
A.12分
B.10分
C.16分
D.14分
二.填空题(共10小题,满分30分,每小题3分)
11.若函数y=(m﹣2)+2是一次函数,那么m=
.
12.已知关于x的方程x2+3x+a=0有一个根为﹣2,则a=
.
13.如图,在平面直角坐标系中,点A(6,0),点B(0,2),点P是直线y=﹣x﹣1上一点,且∠ABP=45°,则点P的坐标为
.
14.在?ABCD中,∠A=30°,AD=4,连接BD,若BD=4,则线段CD的长为
.
15.一次函数y=﹣x+1的图象不经过第
象限.
16.如图,有一块直角三角形木板AOB,∠O=90°,OA=3,OB=4,一只小蚂蚁在OA边上爬行(可以与O、A重合),设其所处的位置C到AB的中点D的距离为x,则x的取值范围是
.
17.如图,AC是菱形ABCD的对角线,P是AC上的一个动点,过点P分别作AB和BC的垂线,垂足分别是点F和E,若菱形的周长是12cm,面积是6cm2,则PE+PF的值是
cm.
18.由于受“一带一路”国家战略策略的影响,某种商品的进口关税连续两次下调,由4000美元下调至2560美元,则平均每次下调的百分率为
.
19.如图,在矩形ABCD中,AB=8,BC=6,点P为边AB上任意一点,过点P作PE⊥AC,PF⊥BD,垂足分别为E、F,则PE+PF=
.
20.若关于x的一元二次方程mx2﹣2x﹣1=0无实数根,则一次函数y=mx+m的图象不经过第
象限.
三.解答题(共7小题,满分60分)
21.解方程:
(1)x2﹣6x﹣9=0;
(2)9(2x+3)2=16(1﹣3x)2.
22.如图,直线l1过点A(0,4),点D(4,0),直线l2:y2=x+1与x轴交于点C,两直线l1,l2相交于点B.
(1)求直线l1的解析式y1;
(2)求直线l1和直线l2的交点B的坐标;
(3)求△ABC的面积;
(4)直接写出当y1>y2时的x的取值范围.
23.如图,在平行四边形ABCD中,点E,F分别在边AD,BC上,AE=CF,求证:BE=DF.
24.如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
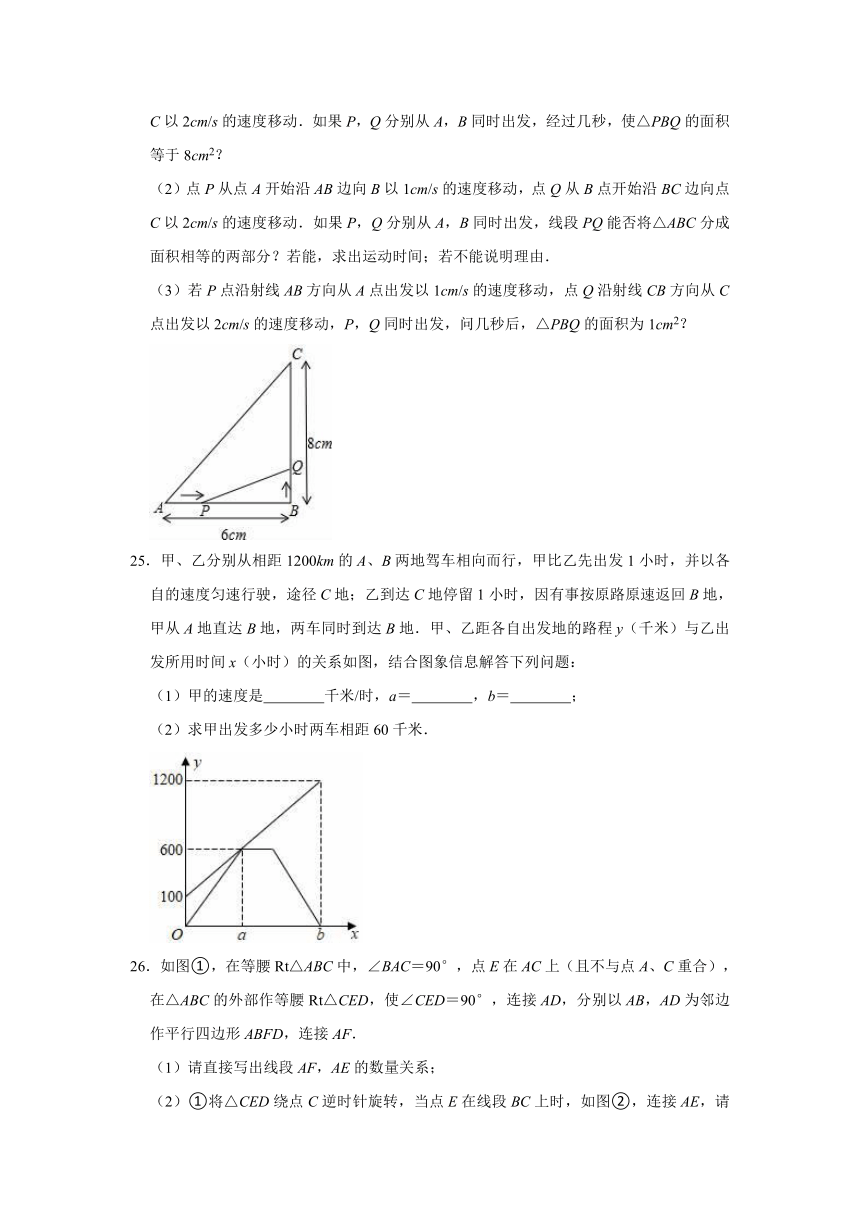
(1)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,经过几秒,使△PBQ的面积等于8cm2?
(2)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
(3)若P点沿射线AB方向从A点出发以1cm/s的速度移动,点Q沿射线CB方向从C点出发以2cm/s的速度移动,P,Q同时出发,问几秒后,△PBQ的面积为1cm2?
25.甲、乙分别从相距1200km的A、B两地驾车相向而行,甲比乙先出发1小时,并以各自的速度匀速行驶,途径C地;乙到达C地停留1小时,因有事按原路原速返回B地,甲从A地直达B地,两车同时到达B地.甲、乙距各自出发地的路程y(千米)与乙出发所用时间x(小时)的关系如图,结合图象信息解答下列问题:
(1)甲的速度是
千米/时,a=
,b=
;
(2)求甲出发多少小时两车相距60千米.
26.如图①,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合),在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系;
(2)①将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
②若AB=2,CE=2,在图②的基础上将△CED绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.
27.如图,在平面直角坐标系中,直线y=﹣2x+12与x轴交于点A,与y轴交于点B,与直线y=x交于点C.
(1)求点C的坐标.
(2)若P是x轴上的一个动点,直接写出当△POC是等腰三角形时P的坐标.
(3)在直线AB上是否存在点M,使得△MOC的面积是△AOC面积的2倍?若存在,请求出点M的坐标;若不存在,请说明理由.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:A、是分式方程,故A错误;
B、是二元二次方程,故B错误;
C、a=0时,是一元一次方程,故C错误;
D、是一元二次方程,故D正确;
故选:D.
2.解:A、∵42+52≠62,∴不能构成直角三角形,故A错误;
B、∵12+12=,∴能构成直角三角形,故B正确;
C、∵62+82≠112,∴不能构成直角三角形,故C错误;
D、∵52+122≠232,∴不能构成直角三角形,故D错误.
故选:B.
3.解:∵直线y=kx+b经过一、二、四象限,
∴k<0,b>0,
∴﹣k>0,
∴选项B中图象符合题意.
故选:B.
4.解:两条平行直线被第三条直线所截,内错角相等,所以①错误;
如果∠1和∠2是对顶角,那么∠1=∠2,所以②正确;
三角形的一个外角大于任何一个不相邻的一个内角,所以③错误;
如果x2>0,那么x≠0,所以④错误.
故选:A.
5.解:设∠ABE=x,
根据折叠前后角相等可知,∠C1BE=∠CBE=50°+x,
所以50°+x+x=90°,
解得x=20°.
故选:B.
6.解:A、1.52+22=2.52,即三角形是直角三角形,故本选项正确;
B、42+52≠62,即三角形不是直角三角形,故本选项错误;
C、22+32≠42,即三角形不是直角三角形,故本选项错误;
D、12+()2≠32,即三角形不是直角三角形,故本选项错误;
故选:A.
7.解:根据题意得,△=b2﹣4ac=[﹣(2m﹣1)]2﹣4m2=﹣4m+1≥0,
解得:m≤,
故选:B.
8.解:∵点(﹣4,y1),(2,y2)都在直线y=x+2上,
∴y1=×(﹣4)+2=﹣2+2=0,y2=×2+2=1+2=3,
∵0<3,
∴y1<y2.
故选:C.
9.解:∵四边形ABCD是正方形,
∴AB=AD,
∵△AEF是等边三角形,
∴AE=AF,
在Rt△ABE和Rt△ADF中,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∵BC=DC,
∴BC﹣BE=CD﹣DF,
∴CE=CF,
∴①说法正确;
∵CE=CF,
∴△ECF是等腰直角三角形,
∴∠CEF=45°,
∵∠AEF=60°,
∴∠AEB=75°,
∴②说法正确;
如图,连接AC,交EF于G点,
∴AC⊥EF,且AC平分EF,
∵∠CAF≠∠DAF,
∴DF≠FG,
∴BE+DF≠EF,
∴③说法错误;
∵EF=2,
∴CE=CF=,
设正方形的边长为a,
在Rt△ADF中,
a2+(a﹣)2=4,
解得a=,
则a2=2+,
∴S正方形ABCD=2+,
④说法正确,
∴正确的有①②④.
故选:C.
10.解:根据函数图象可得:明明骑自行车去上学时,上坡路为1千米,速度为1÷6=千米/分,下坡路程为3﹣1=2千米,速度为2÷(10﹣6)=千米/分,放学后如果按原路返回,且往返过程中,上坡速度相同,下坡速度相同,那么他回来时,上坡路程为2千米,速度为千米/分,下坡路程为1千米,速度为千米/分,
因此走这段路所用的时间为2÷+1÷=14分.
故选:D.
二.填空题(共10小题,满分30分,每小题3分)
11.解:由题意得,m2﹣3=1且m﹣2≠0,
解得:m=±2且m≠2,
∴m=﹣2.
故答案为:﹣2.
12.解:把x=﹣2代入x2+3x+a=0得4﹣6+a=0,解得a=2.
故答案为2.
13.解:将线段BA绕点B顺时针旋转90°得到线段BD,
∵B(0,2),A(6,0),
∴D(﹣2,﹣4),
取AD的中点K(2,﹣2),
直线BK与直线y=﹣x﹣1的交点即为点P.
设直线BK的解析式为y=kx+b,
把B和K的坐标代入得:,
解得:k=﹣2,b=2,
则直线BK的解析式是y=﹣2x+2,
由,解得:,
∴点P坐标为(3,﹣4),
故答案为:(3,﹣4).
14.解:作DE⊥AB于E,如图所示:
∵∠A=30°,
∴DE=AD=2,
∴AE=DE=6,BE===2,
∴AB=AE﹣BE=4,或AB=AE+BE=8,
∵四边形ABCD是平行四边形,
∴CD=AB=4或8;
故答案为:4或8.
15.解:∵一次函数y=﹣x+1中k=﹣1<0,b=1>0,
∴此函数的图象经过一、二、四象限,不经过第三象限.
故答案为:三.
16.解:在Rt△OAB中,AB==5
当C点与点或点A重合时,CD的长最大
∴OD=AD=AB=2.5
当DC⊥AO时,线段CD长最小,此时CD是中位线
∴CD=OB=2
∴2≤x≤2.5.
17.解:连接BP,
(cm2),
∴AB=BC==3(cm),
∴(cm2),
∴,
∴(cm),
故答案为:2.
18.解:设平均每次下调的百分率为x,由题意,得
4000(1﹣x)2=2560,
解得:x1=0.2=20%,x2=1.8(舍去).
故答案是:20%.
19.解:连接OP,如图:
∵四边形ABCD是矩形,
∴∠ABC=90°,OA=OC,OB=OD,AC=BD,
∴OA=OB,AC===10,
∴S矩形ABCD=AB?BC=48,S△AOB=S矩形ABCD=12,OA=OB=5,
∴S△AOB=S△AOP+S△BOP=OA?PE+OB?PF=OA(PE+PF)=×5×(PE+PF)=12,
∴PE+PF=;
故答案为:.
20.解:∵关于x的一元二次方程mx2﹣2x﹣1=0无实数根,
∴m≠0且△=(﹣2)2﹣4m(﹣1)<0,
∴m<﹣1且m≠0,
∴一次函数y=mx+m的图象经过第二、三、四象限,不经过第一象限.
故答案为一.
三.解答题(共7小题,满分60分)
21.解:(1)∵x2﹣6x﹣9=0,
∴x2﹣6x=9,
则x2﹣6x+9=9+9,即(x﹣3)2=18,
∴x﹣3=,
∴x1=3+3,x2=3﹣3;
(2)∵9(2x+3)2=16(1﹣3x)2,
∴3(2x+3)=4(1﹣3x)或3(2x+3)=﹣4(1﹣3x),
解得x1=,x2=.
22.解:(1)设l1的函数关系式为y=kx+b,
根据题意得,
解得k=﹣1,
∴直线l1的解析式为:y=﹣x+4;
(2),
解之得;
所以B(2,2);
(3)当y=0,
x+1=0,
解得:x=﹣2,
则C(﹣2,0),
S△ABC的面积=S△ACD的面积﹣S△BCD的面积=×6×4﹣×6×2=6;
(4)由图象可知,当y1>y2时的x的取值范围是x<2.
23.证明:∵四边形ABCD是平行四边形
∴AD=BC,AD∥BC,
∵AE=CF,
∴DE=BF,
又∵DE∥BF,
∴四边形BEDF是平行四边形,
∴BE=DF.
24.解:(1)设经过x秒,使△PBQ的面积等于8cm2,依题意有
(6﹣x)?2x=8,
解得x1=2,x2=4,
经检验,x1,x2均符合题意.
故经过2秒或4秒,△PBQ的面积等于8cm2;
(2)设经过y秒,线段PQ能否将△ABC分成面积相等的两部分,依题意有
△ABC的面积=×6×8=24,
(6﹣y)?2y=12,
y2﹣6y+12=0,
∵△=b2﹣4ac=36﹣4×12=﹣12<0,
∴此方程无实数根,
∴线段PQ不能否将△ABC分成面积相等的两部分;
(3)①点P在线段AB上,点Q在线段CB上(0<x≤4),
设经过m秒,依题意有
(6﹣m)(8﹣2m)=1,
m2﹣10m+23=0,
解得m1=5+,m2=5﹣,
经检验,m1=5+不符合题意,舍去,
∴m=5﹣;
②点P在线段AB上,点Q在射线CB上(4<x≤6),
设经过n秒,依题意有
(6﹣n)(2n﹣8)=1,
n2﹣10n+25=0,
解得n1=n2=5,
经检验,n=5符合题意.
③点P在射线AB上,点Q在射线CB上(x>6),
设经过k秒,依题意有
(k﹣6)(2k﹣8)=1,
k2﹣10k+23=0,
解得k1=5+,k2=5﹣,
经检验,k1=5﹣不符合题意,舍去,
∴k=5+;
综上所述,经过(5﹣)秒,5秒,(5+)秒后,△PBQ的面积为1cm2.
25.解:(1)由题意得:甲比乙先出发1小时,
∴甲的速度为:100÷1=100(千米/小时),
a=(600﹣100)÷100=5(小时),
b=(1200﹣100)÷100=11(小时).
故答案为:100,5,11;
(2)设y甲=kx+b,把(0,100)和(11,1200)代入,
可得:,
解得:,
∴y甲=100x+100,
①当两车到C地即相遇前,即0<x≤5时,设y=mx,
把(5,600)代入,可得5m=600,
解得:m=120,
∴y乙=120x,
∴当100x+100+120x=1200﹣60时,
x=,
+1=,
∴甲出发小时两车相距60千米;
②当乙车停留在C地时,
100x+100﹣600=60,
解得:x=5.6,
1+5.6=6.6(小时),
∴甲出发6.6小时两车相距60千米;
③两车都朝B地行驶时,设y乙=ax+c,
把(6,600)和(11,0)代入,可得:
,
解得:,
∴y乙=﹣120x+1320,
100x+100﹣(﹣120x+1320)=60,
x=
+1=(小时)
答:甲出发小时或6.6小时或小时两车相距60千米.
26.解:(1)如图①中,结论:AF=AE.
理由:∵四边形ABFD是平行四边形,
∴AB=DF,
∵AB=AC,
∴AC=DF,
∵DE=EC,
∴AE=EF,
∵∠DEC=∠AEF=90°,
∴△AEF是等腰直角三角形,
∴AF=AE.
故答案为AF=AE.
(2)①如图②中,结论:AF=AE.
理由:连接EF,DF交BC于K.
∵四边形ABFD是平行四边形,
∴AB∥DF,
∴∠DKE=∠ABC=45°,
∴∠EKF=180°﹣∠DKE=135°,EK=ED,
∵∠ADE=180°﹣∠EDC=180°﹣45°=135°,
∴∠EKF=∠ADE,
∵∠DKC=∠C,
∴DK=DC,
∵DF=AB=AC,
∴KF=AD,
在△EKF和△EDA中,
,
∴△EKF≌△EDA,
∴EF=EA,∠KEF=∠AED,
∴∠FEA=∠BED=90°,
∴△AEF是等腰直角三角形,
∴AF=AE.
②如图③中,当AD=AC时,四边形ABFD是菱形,设AE交CD于H,易知EH=DH=CH=,AH==3,AE=AH+EH=4,
如图④中当AD=AC时,四边形ABFD是菱形,易知AE=AH﹣EH=3﹣=2,
综上所述,满足条件的AE的长为4或2.
27.解:(1)联立两直线解析式成方程组,得:,
解得:,
∴点C的坐标为(4,4);
(2)设点P(m,0),而点C(4,4),点O(0,0);
PC2=(m﹣4)2+16,PO2=m2,OC2=32;
当PC=PO时,(m﹣4)2+16=m2,解得:m=4;
当PC=OC时,同理可得:m=0(舍去)或8;
当PO=OC时,同理可得:m=;
故点P的坐标为:(4,0)或(8,0)或(,0)或(,0);
(3)当y=0时,有0=﹣2x+12,
解得:x=6,
∴点A的坐标为(6,0),
∴OA=6,
∴S△OAC=×6×4=12.
设M(x,y)当M在x轴下方时,△MOC的面积是△AOC面积的2倍,
∴△MOA的面积等于△AOC的面积,
|y|=4
当y=﹣4时,﹣4=﹣2x+12,x=8,
∴M(8,﹣4),
当M在x轴上方时,△MOC的面积是△AOC面积的2倍,
∴△MOA的面积等于△AOC的面积的3倍,
|y|=12;
当y=12时,12=﹣2x+12,x=0,
∴M(0,12),
综上所述,M(8,﹣4)或(0,12).
一.选择题(共10小题,满分30分,每小题3分)
1.下列方程一定是一元二次方程的是( )
A.3x2+﹣1=0
B.5x2﹣6y﹣3=0
C.ax2﹣x+2=0
D.3x2﹣2x﹣1=0
2.下列各组数中,能构成直角三角形的是( )
A.4,5,6
B.1,1,
C.6,8,11
D.5,12,23
3.若直线y=kx+b经过一、二、四象限,则直线y=bx﹣k的图象只能是图中的( )
A.
B.
C.
D.
4.下列四个命题中,真命题有( )
①两条直线被第三条直线所截,内错角相等.
②如果∠1和∠2是对顶角,那么∠1=∠2.
③三角形的一个外角大于任何一个内角.
④如果x2>0,那么x>0.
A.1个
B.2个
C.3个
D.4个
5.如图:将一个矩形纸片ABCD,沿着BE折叠,使C、D点分别落在点C1,D1处.若∠C1BA=50°,则∠ABE的度数为( )
A.15°
B.20°
C.25°
D.30°
6.下列四组线段中,可以构成直角三角形的是( )
A.1.5,2,2.5
B.4,5,6
C.2,3,4
D.1,,3
7.已知关于x的一元二次方程x2﹣(2m﹣1)x+m2=0有实数根,则m的取值范围是( )
A.m≠0
B.m≤
C.m<
D.m>
8.已知点(﹣4,y1),(2,y2)都在直线y=x+2上,则y1和y2的大小关系是( )
A.y1>y2
B.y1=y2
C.y1<y2
D.无法确定
9.如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上.下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+.其中正确的个数为( )
A.1
B.2
C.3
D.4
10.明明骑自行车去上学时,经过一段先上坡后下坡的路,在这段路上所走的路程s(单位:千米)与时间t(单位:分)之间的函数关系如图所示.放学后如果按原路返回,且往返过程中,上坡速度相同,下坡速度相同,那么他回来时,走这段路所用的时间为( )
A.12分
B.10分
C.16分
D.14分
二.填空题(共10小题,满分30分,每小题3分)
11.若函数y=(m﹣2)+2是一次函数,那么m=
.
12.已知关于x的方程x2+3x+a=0有一个根为﹣2,则a=
.
13.如图,在平面直角坐标系中,点A(6,0),点B(0,2),点P是直线y=﹣x﹣1上一点,且∠ABP=45°,则点P的坐标为
.
14.在?ABCD中,∠A=30°,AD=4,连接BD,若BD=4,则线段CD的长为
.
15.一次函数y=﹣x+1的图象不经过第
象限.
16.如图,有一块直角三角形木板AOB,∠O=90°,OA=3,OB=4,一只小蚂蚁在OA边上爬行(可以与O、A重合),设其所处的位置C到AB的中点D的距离为x,则x的取值范围是
.
17.如图,AC是菱形ABCD的对角线,P是AC上的一个动点,过点P分别作AB和BC的垂线,垂足分别是点F和E,若菱形的周长是12cm,面积是6cm2,则PE+PF的值是
cm.
18.由于受“一带一路”国家战略策略的影响,某种商品的进口关税连续两次下调,由4000美元下调至2560美元,则平均每次下调的百分率为
.
19.如图,在矩形ABCD中,AB=8,BC=6,点P为边AB上任意一点,过点P作PE⊥AC,PF⊥BD,垂足分别为E、F,则PE+PF=
.
20.若关于x的一元二次方程mx2﹣2x﹣1=0无实数根,则一次函数y=mx+m的图象不经过第
象限.
三.解答题(共7小题,满分60分)
21.解方程:
(1)x2﹣6x﹣9=0;
(2)9(2x+3)2=16(1﹣3x)2.
22.如图,直线l1过点A(0,4),点D(4,0),直线l2:y2=x+1与x轴交于点C,两直线l1,l2相交于点B.
(1)求直线l1的解析式y1;
(2)求直线l1和直线l2的交点B的坐标;
(3)求△ABC的面积;
(4)直接写出当y1>y2时的x的取值范围.
23.如图,在平行四边形ABCD中,点E,F分别在边AD,BC上,AE=CF,求证:BE=DF.
24.如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
(1)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,经过几秒,使△PBQ的面积等于8cm2?
(2)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
(3)若P点沿射线AB方向从A点出发以1cm/s的速度移动,点Q沿射线CB方向从C点出发以2cm/s的速度移动,P,Q同时出发,问几秒后,△PBQ的面积为1cm2?
25.甲、乙分别从相距1200km的A、B两地驾车相向而行,甲比乙先出发1小时,并以各自的速度匀速行驶,途径C地;乙到达C地停留1小时,因有事按原路原速返回B地,甲从A地直达B地,两车同时到达B地.甲、乙距各自出发地的路程y(千米)与乙出发所用时间x(小时)的关系如图,结合图象信息解答下列问题:
(1)甲的速度是
千米/时,a=
,b=
;
(2)求甲出发多少小时两车相距60千米.
26.如图①,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合),在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系;
(2)①将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
②若AB=2,CE=2,在图②的基础上将△CED绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.
27.如图,在平面直角坐标系中,直线y=﹣2x+12与x轴交于点A,与y轴交于点B,与直线y=x交于点C.
(1)求点C的坐标.
(2)若P是x轴上的一个动点,直接写出当△POC是等腰三角形时P的坐标.
(3)在直线AB上是否存在点M,使得△MOC的面积是△AOC面积的2倍?若存在,请求出点M的坐标;若不存在,请说明理由.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:A、是分式方程,故A错误;
B、是二元二次方程,故B错误;
C、a=0时,是一元一次方程,故C错误;
D、是一元二次方程,故D正确;
故选:D.
2.解:A、∵42+52≠62,∴不能构成直角三角形,故A错误;
B、∵12+12=,∴能构成直角三角形,故B正确;
C、∵62+82≠112,∴不能构成直角三角形,故C错误;
D、∵52+122≠232,∴不能构成直角三角形,故D错误.
故选:B.
3.解:∵直线y=kx+b经过一、二、四象限,
∴k<0,b>0,
∴﹣k>0,
∴选项B中图象符合题意.
故选:B.
4.解:两条平行直线被第三条直线所截,内错角相等,所以①错误;
如果∠1和∠2是对顶角,那么∠1=∠2,所以②正确;
三角形的一个外角大于任何一个不相邻的一个内角,所以③错误;
如果x2>0,那么x≠0,所以④错误.
故选:A.
5.解:设∠ABE=x,
根据折叠前后角相等可知,∠C1BE=∠CBE=50°+x,
所以50°+x+x=90°,
解得x=20°.
故选:B.
6.解:A、1.52+22=2.52,即三角形是直角三角形,故本选项正确;
B、42+52≠62,即三角形不是直角三角形,故本选项错误;
C、22+32≠42,即三角形不是直角三角形,故本选项错误;
D、12+()2≠32,即三角形不是直角三角形,故本选项错误;
故选:A.
7.解:根据题意得,△=b2﹣4ac=[﹣(2m﹣1)]2﹣4m2=﹣4m+1≥0,
解得:m≤,
故选:B.
8.解:∵点(﹣4,y1),(2,y2)都在直线y=x+2上,
∴y1=×(﹣4)+2=﹣2+2=0,y2=×2+2=1+2=3,
∵0<3,
∴y1<y2.
故选:C.
9.解:∵四边形ABCD是正方形,
∴AB=AD,
∵△AEF是等边三角形,
∴AE=AF,
在Rt△ABE和Rt△ADF中,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∵BC=DC,
∴BC﹣BE=CD﹣DF,
∴CE=CF,
∴①说法正确;
∵CE=CF,
∴△ECF是等腰直角三角形,
∴∠CEF=45°,
∵∠AEF=60°,
∴∠AEB=75°,
∴②说法正确;
如图,连接AC,交EF于G点,
∴AC⊥EF,且AC平分EF,
∵∠CAF≠∠DAF,
∴DF≠FG,
∴BE+DF≠EF,
∴③说法错误;
∵EF=2,
∴CE=CF=,
设正方形的边长为a,
在Rt△ADF中,
a2+(a﹣)2=4,
解得a=,
则a2=2+,
∴S正方形ABCD=2+,
④说法正确,
∴正确的有①②④.
故选:C.
10.解:根据函数图象可得:明明骑自行车去上学时,上坡路为1千米,速度为1÷6=千米/分,下坡路程为3﹣1=2千米,速度为2÷(10﹣6)=千米/分,放学后如果按原路返回,且往返过程中,上坡速度相同,下坡速度相同,那么他回来时,上坡路程为2千米,速度为千米/分,下坡路程为1千米,速度为千米/分,
因此走这段路所用的时间为2÷+1÷=14分.
故选:D.
二.填空题(共10小题,满分30分,每小题3分)
11.解:由题意得,m2﹣3=1且m﹣2≠0,
解得:m=±2且m≠2,
∴m=﹣2.
故答案为:﹣2.
12.解:把x=﹣2代入x2+3x+a=0得4﹣6+a=0,解得a=2.
故答案为2.
13.解:将线段BA绕点B顺时针旋转90°得到线段BD,
∵B(0,2),A(6,0),
∴D(﹣2,﹣4),
取AD的中点K(2,﹣2),
直线BK与直线y=﹣x﹣1的交点即为点P.
设直线BK的解析式为y=kx+b,
把B和K的坐标代入得:,
解得:k=﹣2,b=2,
则直线BK的解析式是y=﹣2x+2,
由,解得:,
∴点P坐标为(3,﹣4),
故答案为:(3,﹣4).
14.解:作DE⊥AB于E,如图所示:
∵∠A=30°,
∴DE=AD=2,
∴AE=DE=6,BE===2,
∴AB=AE﹣BE=4,或AB=AE+BE=8,
∵四边形ABCD是平行四边形,
∴CD=AB=4或8;
故答案为:4或8.
15.解:∵一次函数y=﹣x+1中k=﹣1<0,b=1>0,
∴此函数的图象经过一、二、四象限,不经过第三象限.
故答案为:三.
16.解:在Rt△OAB中,AB==5
当C点与点或点A重合时,CD的长最大
∴OD=AD=AB=2.5
当DC⊥AO时,线段CD长最小,此时CD是中位线
∴CD=OB=2
∴2≤x≤2.5.
17.解:连接BP,
(cm2),
∴AB=BC==3(cm),
∴(cm2),
∴,
∴(cm),
故答案为:2.
18.解:设平均每次下调的百分率为x,由题意,得
4000(1﹣x)2=2560,
解得:x1=0.2=20%,x2=1.8(舍去).
故答案是:20%.
19.解:连接OP,如图:
∵四边形ABCD是矩形,
∴∠ABC=90°,OA=OC,OB=OD,AC=BD,
∴OA=OB,AC===10,
∴S矩形ABCD=AB?BC=48,S△AOB=S矩形ABCD=12,OA=OB=5,
∴S△AOB=S△AOP+S△BOP=OA?PE+OB?PF=OA(PE+PF)=×5×(PE+PF)=12,
∴PE+PF=;
故答案为:.
20.解:∵关于x的一元二次方程mx2﹣2x﹣1=0无实数根,
∴m≠0且△=(﹣2)2﹣4m(﹣1)<0,
∴m<﹣1且m≠0,
∴一次函数y=mx+m的图象经过第二、三、四象限,不经过第一象限.
故答案为一.
三.解答题(共7小题,满分60分)
21.解:(1)∵x2﹣6x﹣9=0,
∴x2﹣6x=9,
则x2﹣6x+9=9+9,即(x﹣3)2=18,
∴x﹣3=,
∴x1=3+3,x2=3﹣3;
(2)∵9(2x+3)2=16(1﹣3x)2,
∴3(2x+3)=4(1﹣3x)或3(2x+3)=﹣4(1﹣3x),
解得x1=,x2=.
22.解:(1)设l1的函数关系式为y=kx+b,
根据题意得,
解得k=﹣1,
∴直线l1的解析式为:y=﹣x+4;
(2),
解之得;
所以B(2,2);
(3)当y=0,
x+1=0,
解得:x=﹣2,
则C(﹣2,0),
S△ABC的面积=S△ACD的面积﹣S△BCD的面积=×6×4﹣×6×2=6;
(4)由图象可知,当y1>y2时的x的取值范围是x<2.
23.证明:∵四边形ABCD是平行四边形
∴AD=BC,AD∥BC,
∵AE=CF,
∴DE=BF,
又∵DE∥BF,
∴四边形BEDF是平行四边形,
∴BE=DF.
24.解:(1)设经过x秒,使△PBQ的面积等于8cm2,依题意有
(6﹣x)?2x=8,
解得x1=2,x2=4,
经检验,x1,x2均符合题意.
故经过2秒或4秒,△PBQ的面积等于8cm2;
(2)设经过y秒,线段PQ能否将△ABC分成面积相等的两部分,依题意有
△ABC的面积=×6×8=24,
(6﹣y)?2y=12,
y2﹣6y+12=0,
∵△=b2﹣4ac=36﹣4×12=﹣12<0,
∴此方程无实数根,
∴线段PQ不能否将△ABC分成面积相等的两部分;
(3)①点P在线段AB上,点Q在线段CB上(0<x≤4),
设经过m秒,依题意有
(6﹣m)(8﹣2m)=1,
m2﹣10m+23=0,
解得m1=5+,m2=5﹣,
经检验,m1=5+不符合题意,舍去,
∴m=5﹣;
②点P在线段AB上,点Q在射线CB上(4<x≤6),
设经过n秒,依题意有
(6﹣n)(2n﹣8)=1,
n2﹣10n+25=0,
解得n1=n2=5,
经检验,n=5符合题意.
③点P在射线AB上,点Q在射线CB上(x>6),
设经过k秒,依题意有
(k﹣6)(2k﹣8)=1,
k2﹣10k+23=0,
解得k1=5+,k2=5﹣,
经检验,k1=5﹣不符合题意,舍去,
∴k=5+;
综上所述,经过(5﹣)秒,5秒,(5+)秒后,△PBQ的面积为1cm2.
25.解:(1)由题意得:甲比乙先出发1小时,
∴甲的速度为:100÷1=100(千米/小时),
a=(600﹣100)÷100=5(小时),
b=(1200﹣100)÷100=11(小时).
故答案为:100,5,11;
(2)设y甲=kx+b,把(0,100)和(11,1200)代入,
可得:,
解得:,
∴y甲=100x+100,
①当两车到C地即相遇前,即0<x≤5时,设y=mx,
把(5,600)代入,可得5m=600,
解得:m=120,
∴y乙=120x,
∴当100x+100+120x=1200﹣60时,
x=,
+1=,
∴甲出发小时两车相距60千米;
②当乙车停留在C地时,
100x+100﹣600=60,
解得:x=5.6,
1+5.6=6.6(小时),
∴甲出发6.6小时两车相距60千米;
③两车都朝B地行驶时,设y乙=ax+c,
把(6,600)和(11,0)代入,可得:
,
解得:,
∴y乙=﹣120x+1320,
100x+100﹣(﹣120x+1320)=60,
x=
+1=(小时)
答:甲出发小时或6.6小时或小时两车相距60千米.
26.解:(1)如图①中,结论:AF=AE.
理由:∵四边形ABFD是平行四边形,
∴AB=DF,
∵AB=AC,
∴AC=DF,
∵DE=EC,
∴AE=EF,
∵∠DEC=∠AEF=90°,
∴△AEF是等腰直角三角形,
∴AF=AE.
故答案为AF=AE.
(2)①如图②中,结论:AF=AE.
理由:连接EF,DF交BC于K.
∵四边形ABFD是平行四边形,
∴AB∥DF,
∴∠DKE=∠ABC=45°,
∴∠EKF=180°﹣∠DKE=135°,EK=ED,
∵∠ADE=180°﹣∠EDC=180°﹣45°=135°,
∴∠EKF=∠ADE,
∵∠DKC=∠C,
∴DK=DC,
∵DF=AB=AC,
∴KF=AD,
在△EKF和△EDA中,
,
∴△EKF≌△EDA,
∴EF=EA,∠KEF=∠AED,
∴∠FEA=∠BED=90°,
∴△AEF是等腰直角三角形,
∴AF=AE.
②如图③中,当AD=AC时,四边形ABFD是菱形,设AE交CD于H,易知EH=DH=CH=,AH==3,AE=AH+EH=4,
如图④中当AD=AC时,四边形ABFD是菱形,易知AE=AH﹣EH=3﹣=2,
综上所述,满足条件的AE的长为4或2.
27.解:(1)联立两直线解析式成方程组,得:,
解得:,
∴点C的坐标为(4,4);
(2)设点P(m,0),而点C(4,4),点O(0,0);
PC2=(m﹣4)2+16,PO2=m2,OC2=32;
当PC=PO时,(m﹣4)2+16=m2,解得:m=4;
当PC=OC时,同理可得:m=0(舍去)或8;
当PO=OC时,同理可得:m=;
故点P的坐标为:(4,0)或(8,0)或(,0)或(,0);
(3)当y=0时,有0=﹣2x+12,
解得:x=6,
∴点A的坐标为(6,0),
∴OA=6,
∴S△OAC=×6×4=12.
设M(x,y)当M在x轴下方时,△MOC的面积是△AOC面积的2倍,
∴△MOA的面积等于△AOC的面积,
|y|=4
当y=﹣4时,﹣4=﹣2x+12,x=8,
∴M(8,﹣4),
当M在x轴上方时,△MOC的面积是△AOC面积的2倍,
∴△MOA的面积等于△AOC的面积的3倍,
|y|=12;
当y=12时,12=﹣2x+12,x=0,
∴M(0,12),
综上所述,M(8,﹣4)或(0,12).
同课章节目录
