2020-2021学年人教五四新版六年级下册数学期末练习试题(Word版含解析)
文档属性
| 名称 | 2020-2021学年人教五四新版六年级下册数学期末练习试题(Word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 201.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-17 00:00:00 | ||
图片预览




文档简介
2020-2021学年人教五四新版六年级下册数学期末练习试题
一.选择题(共10小题,满分30分,每小题3分)
1.当A地高于海平面152米时,记作“海拔+152米”,那么B地低于海平面23米时,记作( )
A.海拔23米
B.海拔﹣23米
C.海拔175米
D.海拔129米
2.﹣4的相反数是( )
A.
B.4
C.
D.﹣4
3.下列整式中,单项式是( )
A.3a+1
B.2x﹣y
C.3a
D.
4.下列说法正确的是( )
A.延长直线AB到点C
B.延长射线AB到点C
C.延长线段AB到点C
D.射线AB与射线BA是同一条射线
5.如图所示几何体的左视图正确的是( )
A.
B.
C.
D.
6.在新冠肺炎防控期间,要了解某学校以下情况,其中适合用普查的有( )
①了解学校口罩、洗手液、消毒片的储备情况;
②了解全体师生在寒假期间的离校情况;
③了解全体师生入校时的体温情况;
④了解全体师生对“七步洗手法”的运用情况.
A.1个
B.2个
C.3个
D.4个
7.下列各式中,是5x2y的同类项的是( )
A.3a2b
B.x3
C.﹣x2y
D.5x2yz
8.用四舍五入法对2020.89(精确到十分位)取近似数的结果是( )
A.2020
B.2020.8
C.2020.9
D.2020.89
9.已知有理数a,b在数轴上表示的点如图所示,则下列式子中正确的是( )
A.a+b<0
B.a+b>0
C.a﹣b<0
D.ab>0
10.下列说法中,正确的个数为( )
(1)两点之间,线段最短
(2)多项式ab2﹣3a2+1的次数是5次
(3)若AB=BC,则点B是线段AC的中点
(4)数字0也是单项式.
A.1个
B.2个
C.3个
D.4个
二.填空题(共10小题,满分30分,每小题3分)
11.5G是第五代移动通信技术,其网络下载速度可以达到每秒1300000KB以上,正常下载一部高清电影约需1秒.将1300000用科学记数法表示为
.
12.比较大小:
(用“>或=或<”填空).
13.﹣2x2y单项式的次数是
.
14.如果一个角的补角是这个角的余角的3倍,则这个角是
.
15.为了解无锡市八年级学生的身高情况,从中任意抽取2000名学生的身高进行统计,在这个问题中,样本容量是
.
16.已知M是线段AB的中点,AM=6cm,则AB=
cm.
17.一个多项式加上﹣2a+6等于2a2+a+3,则这个多项式是
.
18.规定?是一种新运算规则:a?b=a2﹣b2,例如:2?3=22﹣32=4﹣9=﹣5,则5?[1?(﹣2)]=
.
19.如图,这是用黑白棋子组成的一组图案,第1个图案由1个黑子组成,第2个图案由1个黑子和6个白子组成,第3个图案由13个黑子和6个白子组成…按照这样的规律排列下去,则第6个图案中共有
个白子.
20.已知,∠AOB=2∠BOC,∠BOC=30°,则∠AOC的度数是
.
三.解答题(共7小题,满分60分)
21.计算:
(1)|﹣|÷(﹣)﹣×(﹣2)3;
(2)(﹣+)÷(﹣).
22.先化简,再求值:3y2﹣x2+2(2x2﹣3xy)﹣3(x2+y2)的值,其中x=1,y=﹣2.
23.如图,已知直线l和直线外三点A,B,C,按下列要求画图,填空:
(1)画射线AB;
(2)连接BC;
(3)延长CB至D,使得BD=BC;
(4)在直线上确定点E,使得AE+CE最小,请写出你作图的依据
.
24.一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:
(单位:米)+5,﹣4,+10,﹣8,﹣6,+13,﹣10.
(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门线最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
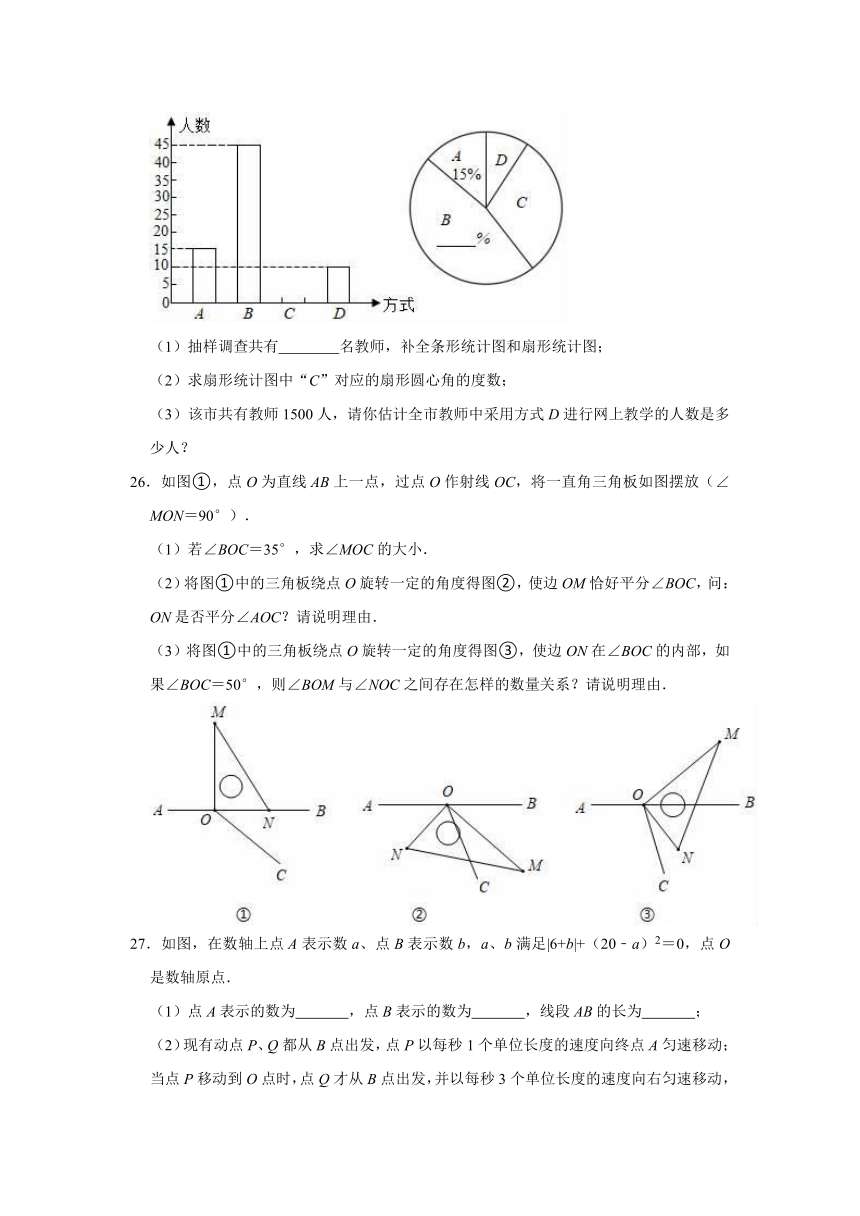
25.2020年3月黑龙江省实现线上教学,教师采用了不同的直播方式.A:用电视投屏加直播讲解;B:用电脑直播加课件演示;C:用手机直播加纸笔板演;D:用视频会议加课件探讨,孩子们领略到新奇的开放的网络课堂.某市教育局为了了解教师的直播方式情况,教育局从全市教师队伍中随机抽取了部分教师进行了一次调查(每位教师只能从四个直播方式中选择一种),并根据调查结果绘制成如图所示的两幅不完整的统计图.请结合图中信息回答下列问题:
(1)抽样调查共有
名教师,补全条形统计图和扇形统计图;
(2)求扇形统计图中“C”对应的扇形圆心角的度数;
(3)该市共有教师1500人,请你估计全市教师中采用方式D进行网上教学的人数是多少人?
26.如图①,点O为直线AB上一点,过点O作射线OC,将一直角三角板如图摆放(∠MON=90°).
(1)若∠BOC=35°,求∠MOC的大小.
(2)将图①中的三角板绕点O旋转一定的角度得图②,使边OM恰好平分∠BOC,问:ON是否平分∠AOC?请说明理由.
(3)将图①中的三角板绕点O旋转一定的角度得图③,使边ON在∠BOC的内部,如果∠BOC=50°,则∠BOM与∠NOC之间存在怎样的数量关系?请说明理由.
27.如图,在数轴上点A表示数a、点B表示数b,a、b满足|6+b|+(20﹣a)2=0,点O是数轴原点.
(1)点A表示的数为
,点B表示的数为
,线段AB的长为
;
(2)现有动点P、Q都从B点出发,点P以每秒1个单位长度的速度向终点A匀速移动;当点P移动到O点时,点Q才从B点出发,并以每秒3个单位长度的速度向右匀速移动,且当点P到达A点时,点Q就停止移动,设点P移动的时间为t秒.
①当t=
时,点P移动到O点;
②求当t为多少时,P、Q两点相距4个单位长度.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:A地高于海平面152米时,记作“海拔+152米”,那么B地低于海平面23米时,记作海拔﹣23米,
故选:B.
2.解:﹣4的相反数是:4.
故选:B.
3.解:A、3a+1是多项式,不是单项式,故本选项不符合题意;
B、2x﹣y是多项式,不是单项式,故本选项不符合题意;
C、3a是单项式,故本选项符合题意;
D、是多项式,不是单项式,故本选项不符合题意;
故选:C.
4.解:A、直线可以沿两个方向无限延伸,故不能说延长直线AB,故本选项不符合题意;
B、射线可沿延伸方向无限延伸,故不能说延长射线AB,故本选项不符合题意;
C、线段不能延伸,可以说延长线段AB到点C,故本选项符合题意;
D、射线AB与射线BA不是同一条射线,故本选项不符合题意;
故选:C.
5.解:从几何体的左面看所得到的图形是:
故选:A.
6.解:①了解学校口罩、洗手液、消毒片的储备情况适合普查;
②了解全体师生在寒假期间的离锡情况适合普查;
③了解全体师生入校时的体温情况适合普查;
④了解全体师生对“七步洗手法”的运用情况适合抽样调查.
故选:C.
7.解:A、5x2y与3a2b,所含的字母不相同,所以它们不是同类项,故本选项不合题意;
B、5x2y与x3,所含的字母不相同,所以它们不是同类项,故本选项不合题意;
C、5x2y与﹣x2y,所含的字母相同,相同字母的指数也相同,是同类项,故本选项符合题意;
D、5x2y与5x2yz,所含的字母不相同,所以它们不是同类项,故本选项不合题意.
故选:C.
8.解:2020.89(精确到十分位)取近似数的结果是2020.9.
故选:C.
9.解:从图上可以看出,b<﹣1<0,0<a<1,
∴a+b<0,故选项A符合题意,选项B不合题意;
a﹣b>0,故选项C不合题意;
ab<0,故选项D不合题意.
故选:A.
10.解:(1)两点之间,线段最短,正确;
(2)多项式ab2﹣3a2+1的次数是3次,故此选项错误;
(3)若AB=BC,则点B是线段AC的中点,错误,A,B,C可能不在同一条直线上,故此选项错误;
(4)数字0也是单项式,正确.
则正确的有2个.
故选:B.
二.填空题(共10小题,满分30分,每小题3分)
11.解:将数据1300000用科学记数法可表示为:1.3×106.
故答案为:1.3×106.
12.解:∵||==,|﹣|==,
∴|﹣|>||;
∴﹣<﹣.
故答案为<.
13.解:﹣2x2y单项式的次数是1+2=3,
故答案为:3.
14.解:设这个角为x,
由题意得,180°﹣x=3(90°﹣x),
解得x=45°,
则这个角是45°,
故答案为:45°.
15.解:为了解无锡市八年级学生的身高情况,从中任意抽取2000名学生的身高进行统计,在这个问题中,样本容量是2000.
故答案为:2000.
16.解:∵M是线段AB的中点,AM=6cm,
∴AB=2AM=2×6=12(cm),
故答案为:12.
17.解:∵一个多项式加上﹣2a+6等于2a2+a+3,
∴这个多项式是:2a2+a+3﹣(﹣2a+6)
=2a2+a+3+2a﹣6
=2a2+3a﹣3.
故答案为:2a2+3a﹣3.
18.解:根据题中的新定义得:原式=5?(1﹣4)=5?(﹣3)=25﹣9=16.
故答案为:16.
19.解:第1个图案由1个黑子组成,
第2个图案由1个黑子和6个白子组成,
第3个图案由1+3×6﹣6=13个黑子和6个白子组成,
第4个图案由13个黑子和6+4×6﹣6=24个白子组成,
第5个图案由13+5×6﹣6=37个黑子和24个白子组成,
第6个图案由37个黑子和24+6×6﹣6=54个白子组成.
故答案为54.
20.解:分两种情况考虑.
当OB在∠AOC中时,如图1所示,
∵∠AOB=2∠BOC=2×30°=60°,
∴∠AOC=∠AOB+∠BOC=60°+30°=90°;
当OC在∠AOB中时,如图2所示,
∵∠AOB=2∠BOC=2×30°=60°,
∴∠AOC=∠AOB﹣∠BOC=60°﹣30°=30°.
故答案为:90°或30°.
三.解答题(共7小题,满分60分)
21.解:(1)|﹣|÷(﹣)﹣×(﹣2)3
=÷(﹣)﹣×(﹣8)
=﹣2+1
=﹣1.
(2)(﹣+)÷(﹣)
=×(﹣24)﹣×(﹣24)+×(﹣24)
=﹣16+18﹣4
=﹣2.
22.解:3y2﹣x2+2(2x2﹣3xy)﹣3(x2+y2)
=3y2﹣x2+4x2﹣6xy﹣3x2﹣3y2
=﹣6xy
当x=1,y=﹣2时,原式=﹣6×1×(﹣2)=12.
23.解:(1)射线AB如图所示.
(2)线段BC如图所示.
(3)线段BD如图所示.
(4)连接AC交直线l于点E,此时AE+EC的值最小.理由:两点之间线段最短.
故答案为两点之间线段最短.
24.解:(1)(+5)+(﹣4)+(+10)+(﹣8)+(﹣6)+(+13)+(﹣10)=0.
答:守门员最后回到了球门线的位置;
(2)
第1次
第2次
第3次
第4次
第5次
第6次
第7次
5
1
11
3
﹣3
10
0
答:在练习过程中,守门员离开球门线最远距离是11米;
(3)|+5|+|﹣4|+|+10|+|﹣8|+|﹣6|+|+13|+|﹣10|
=5+4+10+8+6+13+10
=56(米).
答:守门员全部练习结束后,他共跑了56米.
25.解:(1)15÷15%=100(名),100﹣45﹣15﹣10=30(名),
45÷100=45%,
故答案为:100,补全条形统计图如图所示:
补全扇形统计图如图所示,
(2)360°×=108°,
答:扇形统计图中“C”对应的扇形圆心角的度数为108°;
(3)1500×=150(人),
答:市1500名教师采用方式D进行网上教学的有150人.
26.解:(1)∵∠MON=90°,∠BOC=35°,
∴∠MOC=∠MON+∠BOC=90°+35°=125°.
(2)ON平分∠AOC.理由如下:
∵∠MON=90°,
∴∠BOM+∠AON=90°,∠MOC+∠NOC=90°.
又∵OM平分∠BOC,
∴∠BOM=∠MOC.
∴∠AON=∠NOC.
∴ON平分∠AOC.
(3)∠BOM=∠NOC+40°.理由如下:
∵∠CON+∠NOB=50°,
∴∠NOB=50°﹣∠NOC.
∵∠BOM+∠NOB=90°,
∴∠BOM=90°﹣∠NOB=90°﹣(50°﹣∠NOC)=∠NOC+40°.
27.解:(1)∵|6+b|+(20﹣a)2=0,
∴20﹣a=0,6+b=0,
解得a=20,b=﹣6,
AB=20﹣(﹣6)=26.
故点A表示的数为20,点B表示的数为﹣6,线段AB的长为26.
故答案为:20,﹣6,26;
(2)①依题意有t=0﹣(﹣6),
解得t=6.
故当t=6时,点P移动到O点;
故答案为:6;
②经过t秒后,点P表示的数为t﹣6,点Q表示的数为,
(i)当0<t≤6时,点Q还在点B处,
∴PQ=t﹣6﹣(﹣6)=t=4;
(ii)当6<x≤9时,点P在点Q的右侧,
∴(t﹣6)﹣[3(t﹣6)﹣6]=4,
解得:t=7;
(iii)当9<t≤26时,点P在点Q的左侧,
∴3(t﹣6)﹣6﹣(t﹣6)=4,
解得:t=11.
综上所述:当t为4或7或11时,P、Q两点相距4个单位长度.
一.选择题(共10小题,满分30分,每小题3分)
1.当A地高于海平面152米时,记作“海拔+152米”,那么B地低于海平面23米时,记作( )
A.海拔23米
B.海拔﹣23米
C.海拔175米
D.海拔129米
2.﹣4的相反数是( )
A.
B.4
C.
D.﹣4
3.下列整式中,单项式是( )
A.3a+1
B.2x﹣y
C.3a
D.
4.下列说法正确的是( )
A.延长直线AB到点C
B.延长射线AB到点C
C.延长线段AB到点C
D.射线AB与射线BA是同一条射线
5.如图所示几何体的左视图正确的是( )
A.
B.
C.
D.
6.在新冠肺炎防控期间,要了解某学校以下情况,其中适合用普查的有( )
①了解学校口罩、洗手液、消毒片的储备情况;
②了解全体师生在寒假期间的离校情况;
③了解全体师生入校时的体温情况;
④了解全体师生对“七步洗手法”的运用情况.
A.1个
B.2个
C.3个
D.4个
7.下列各式中,是5x2y的同类项的是( )
A.3a2b
B.x3
C.﹣x2y
D.5x2yz
8.用四舍五入法对2020.89(精确到十分位)取近似数的结果是( )
A.2020
B.2020.8
C.2020.9
D.2020.89
9.已知有理数a,b在数轴上表示的点如图所示,则下列式子中正确的是( )
A.a+b<0
B.a+b>0
C.a﹣b<0
D.ab>0
10.下列说法中,正确的个数为( )
(1)两点之间,线段最短
(2)多项式ab2﹣3a2+1的次数是5次
(3)若AB=BC,则点B是线段AC的中点
(4)数字0也是单项式.
A.1个
B.2个
C.3个
D.4个
二.填空题(共10小题,满分30分,每小题3分)
11.5G是第五代移动通信技术,其网络下载速度可以达到每秒1300000KB以上,正常下载一部高清电影约需1秒.将1300000用科学记数法表示为
.
12.比较大小:
(用“>或=或<”填空).
13.﹣2x2y单项式的次数是
.
14.如果一个角的补角是这个角的余角的3倍,则这个角是
.
15.为了解无锡市八年级学生的身高情况,从中任意抽取2000名学生的身高进行统计,在这个问题中,样本容量是
.
16.已知M是线段AB的中点,AM=6cm,则AB=
cm.
17.一个多项式加上﹣2a+6等于2a2+a+3,则这个多项式是
.
18.规定?是一种新运算规则:a?b=a2﹣b2,例如:2?3=22﹣32=4﹣9=﹣5,则5?[1?(﹣2)]=
.
19.如图,这是用黑白棋子组成的一组图案,第1个图案由1个黑子组成,第2个图案由1个黑子和6个白子组成,第3个图案由13个黑子和6个白子组成…按照这样的规律排列下去,则第6个图案中共有
个白子.
20.已知,∠AOB=2∠BOC,∠BOC=30°,则∠AOC的度数是
.
三.解答题(共7小题,满分60分)
21.计算:
(1)|﹣|÷(﹣)﹣×(﹣2)3;
(2)(﹣+)÷(﹣).
22.先化简,再求值:3y2﹣x2+2(2x2﹣3xy)﹣3(x2+y2)的值,其中x=1,y=﹣2.
23.如图,已知直线l和直线外三点A,B,C,按下列要求画图,填空:
(1)画射线AB;
(2)连接BC;
(3)延长CB至D,使得BD=BC;
(4)在直线上确定点E,使得AE+CE最小,请写出你作图的依据
.
24.一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:
(单位:米)+5,﹣4,+10,﹣8,﹣6,+13,﹣10.
(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门线最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
25.2020年3月黑龙江省实现线上教学,教师采用了不同的直播方式.A:用电视投屏加直播讲解;B:用电脑直播加课件演示;C:用手机直播加纸笔板演;D:用视频会议加课件探讨,孩子们领略到新奇的开放的网络课堂.某市教育局为了了解教师的直播方式情况,教育局从全市教师队伍中随机抽取了部分教师进行了一次调查(每位教师只能从四个直播方式中选择一种),并根据调查结果绘制成如图所示的两幅不完整的统计图.请结合图中信息回答下列问题:
(1)抽样调查共有
名教师,补全条形统计图和扇形统计图;
(2)求扇形统计图中“C”对应的扇形圆心角的度数;
(3)该市共有教师1500人,请你估计全市教师中采用方式D进行网上教学的人数是多少人?
26.如图①,点O为直线AB上一点,过点O作射线OC,将一直角三角板如图摆放(∠MON=90°).
(1)若∠BOC=35°,求∠MOC的大小.
(2)将图①中的三角板绕点O旋转一定的角度得图②,使边OM恰好平分∠BOC,问:ON是否平分∠AOC?请说明理由.
(3)将图①中的三角板绕点O旋转一定的角度得图③,使边ON在∠BOC的内部,如果∠BOC=50°,则∠BOM与∠NOC之间存在怎样的数量关系?请说明理由.
27.如图,在数轴上点A表示数a、点B表示数b,a、b满足|6+b|+(20﹣a)2=0,点O是数轴原点.
(1)点A表示的数为
,点B表示的数为
,线段AB的长为
;
(2)现有动点P、Q都从B点出发,点P以每秒1个单位长度的速度向终点A匀速移动;当点P移动到O点时,点Q才从B点出发,并以每秒3个单位长度的速度向右匀速移动,且当点P到达A点时,点Q就停止移动,设点P移动的时间为t秒.
①当t=
时,点P移动到O点;
②求当t为多少时,P、Q两点相距4个单位长度.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:A地高于海平面152米时,记作“海拔+152米”,那么B地低于海平面23米时,记作海拔﹣23米,
故选:B.
2.解:﹣4的相反数是:4.
故选:B.
3.解:A、3a+1是多项式,不是单项式,故本选项不符合题意;
B、2x﹣y是多项式,不是单项式,故本选项不符合题意;
C、3a是单项式,故本选项符合题意;
D、是多项式,不是单项式,故本选项不符合题意;
故选:C.
4.解:A、直线可以沿两个方向无限延伸,故不能说延长直线AB,故本选项不符合题意;
B、射线可沿延伸方向无限延伸,故不能说延长射线AB,故本选项不符合题意;
C、线段不能延伸,可以说延长线段AB到点C,故本选项符合题意;
D、射线AB与射线BA不是同一条射线,故本选项不符合题意;
故选:C.
5.解:从几何体的左面看所得到的图形是:
故选:A.
6.解:①了解学校口罩、洗手液、消毒片的储备情况适合普查;
②了解全体师生在寒假期间的离锡情况适合普查;
③了解全体师生入校时的体温情况适合普查;
④了解全体师生对“七步洗手法”的运用情况适合抽样调查.
故选:C.
7.解:A、5x2y与3a2b,所含的字母不相同,所以它们不是同类项,故本选项不合题意;
B、5x2y与x3,所含的字母不相同,所以它们不是同类项,故本选项不合题意;
C、5x2y与﹣x2y,所含的字母相同,相同字母的指数也相同,是同类项,故本选项符合题意;
D、5x2y与5x2yz,所含的字母不相同,所以它们不是同类项,故本选项不合题意.
故选:C.
8.解:2020.89(精确到十分位)取近似数的结果是2020.9.
故选:C.
9.解:从图上可以看出,b<﹣1<0,0<a<1,
∴a+b<0,故选项A符合题意,选项B不合题意;
a﹣b>0,故选项C不合题意;
ab<0,故选项D不合题意.
故选:A.
10.解:(1)两点之间,线段最短,正确;
(2)多项式ab2﹣3a2+1的次数是3次,故此选项错误;
(3)若AB=BC,则点B是线段AC的中点,错误,A,B,C可能不在同一条直线上,故此选项错误;
(4)数字0也是单项式,正确.
则正确的有2个.
故选:B.
二.填空题(共10小题,满分30分,每小题3分)
11.解:将数据1300000用科学记数法可表示为:1.3×106.
故答案为:1.3×106.
12.解:∵||==,|﹣|==,
∴|﹣|>||;
∴﹣<﹣.
故答案为<.
13.解:﹣2x2y单项式的次数是1+2=3,
故答案为:3.
14.解:设这个角为x,
由题意得,180°﹣x=3(90°﹣x),
解得x=45°,
则这个角是45°,
故答案为:45°.
15.解:为了解无锡市八年级学生的身高情况,从中任意抽取2000名学生的身高进行统计,在这个问题中,样本容量是2000.
故答案为:2000.
16.解:∵M是线段AB的中点,AM=6cm,
∴AB=2AM=2×6=12(cm),
故答案为:12.
17.解:∵一个多项式加上﹣2a+6等于2a2+a+3,
∴这个多项式是:2a2+a+3﹣(﹣2a+6)
=2a2+a+3+2a﹣6
=2a2+3a﹣3.
故答案为:2a2+3a﹣3.
18.解:根据题中的新定义得:原式=5?(1﹣4)=5?(﹣3)=25﹣9=16.
故答案为:16.
19.解:第1个图案由1个黑子组成,
第2个图案由1个黑子和6个白子组成,
第3个图案由1+3×6﹣6=13个黑子和6个白子组成,
第4个图案由13个黑子和6+4×6﹣6=24个白子组成,
第5个图案由13+5×6﹣6=37个黑子和24个白子组成,
第6个图案由37个黑子和24+6×6﹣6=54个白子组成.
故答案为54.
20.解:分两种情况考虑.
当OB在∠AOC中时,如图1所示,
∵∠AOB=2∠BOC=2×30°=60°,
∴∠AOC=∠AOB+∠BOC=60°+30°=90°;
当OC在∠AOB中时,如图2所示,
∵∠AOB=2∠BOC=2×30°=60°,
∴∠AOC=∠AOB﹣∠BOC=60°﹣30°=30°.
故答案为:90°或30°.
三.解答题(共7小题,满分60分)
21.解:(1)|﹣|÷(﹣)﹣×(﹣2)3
=÷(﹣)﹣×(﹣8)
=﹣2+1
=﹣1.
(2)(﹣+)÷(﹣)
=×(﹣24)﹣×(﹣24)+×(﹣24)
=﹣16+18﹣4
=﹣2.
22.解:3y2﹣x2+2(2x2﹣3xy)﹣3(x2+y2)
=3y2﹣x2+4x2﹣6xy﹣3x2﹣3y2
=﹣6xy
当x=1,y=﹣2时,原式=﹣6×1×(﹣2)=12.
23.解:(1)射线AB如图所示.
(2)线段BC如图所示.
(3)线段BD如图所示.
(4)连接AC交直线l于点E,此时AE+EC的值最小.理由:两点之间线段最短.
故答案为两点之间线段最短.
24.解:(1)(+5)+(﹣4)+(+10)+(﹣8)+(﹣6)+(+13)+(﹣10)=0.
答:守门员最后回到了球门线的位置;
(2)
第1次
第2次
第3次
第4次
第5次
第6次
第7次
5
1
11
3
﹣3
10
0
答:在练习过程中,守门员离开球门线最远距离是11米;
(3)|+5|+|﹣4|+|+10|+|﹣8|+|﹣6|+|+13|+|﹣10|
=5+4+10+8+6+13+10
=56(米).
答:守门员全部练习结束后,他共跑了56米.
25.解:(1)15÷15%=100(名),100﹣45﹣15﹣10=30(名),
45÷100=45%,
故答案为:100,补全条形统计图如图所示:
补全扇形统计图如图所示,
(2)360°×=108°,
答:扇形统计图中“C”对应的扇形圆心角的度数为108°;
(3)1500×=150(人),
答:市1500名教师采用方式D进行网上教学的有150人.
26.解:(1)∵∠MON=90°,∠BOC=35°,
∴∠MOC=∠MON+∠BOC=90°+35°=125°.
(2)ON平分∠AOC.理由如下:
∵∠MON=90°,
∴∠BOM+∠AON=90°,∠MOC+∠NOC=90°.
又∵OM平分∠BOC,
∴∠BOM=∠MOC.
∴∠AON=∠NOC.
∴ON平分∠AOC.
(3)∠BOM=∠NOC+40°.理由如下:
∵∠CON+∠NOB=50°,
∴∠NOB=50°﹣∠NOC.
∵∠BOM+∠NOB=90°,
∴∠BOM=90°﹣∠NOB=90°﹣(50°﹣∠NOC)=∠NOC+40°.
27.解:(1)∵|6+b|+(20﹣a)2=0,
∴20﹣a=0,6+b=0,
解得a=20,b=﹣6,
AB=20﹣(﹣6)=26.
故点A表示的数为20,点B表示的数为﹣6,线段AB的长为26.
故答案为:20,﹣6,26;
(2)①依题意有t=0﹣(﹣6),
解得t=6.
故当t=6时,点P移动到O点;
故答案为:6;
②经过t秒后,点P表示的数为t﹣6,点Q表示的数为,
(i)当0<t≤6时,点Q还在点B处,
∴PQ=t﹣6﹣(﹣6)=t=4;
(ii)当6<x≤9时,点P在点Q的右侧,
∴(t﹣6)﹣[3(t﹣6)﹣6]=4,
解得:t=7;
(iii)当9<t≤26时,点P在点Q的左侧,
∴3(t﹣6)﹣6﹣(t﹣6)=4,
解得:t=11.
综上所述:当t为4或7或11时,P、Q两点相距4个单位长度.
同课章节目录
