人教版六年级数学上册9.2 图形与几何 课件(21张ppt)
文档属性
| 名称 | 人教版六年级数学上册9.2 图形与几何 课件(21张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 965.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-01 00:00:00 | ||
图片预览

文档简介
总 复 习
2 图形与几何
一、回顾整理
确定物体位置的条件
描述并绘制简单的路线图
在平面图上确定物体的位置
想一想,关于位置与方向学了哪些知识?
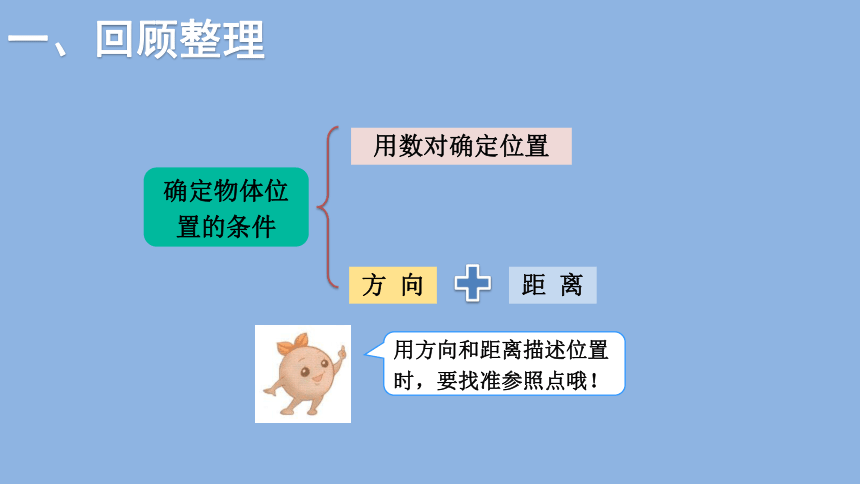
一、回顾整理
确定物体位置的条件
方 向
距 离
用数对确定位置
用方向和距离描述位置时,要找准参照点哦!
再以选定的单位长度确定
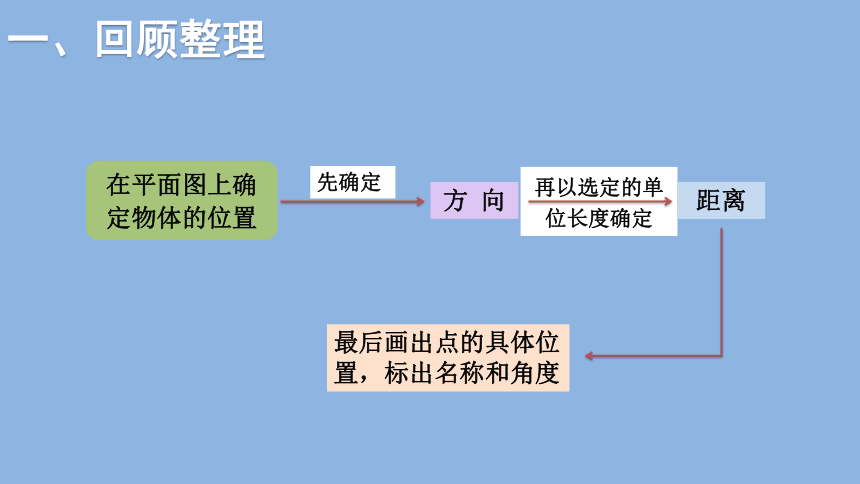
一、回顾整理
在平面图上确定物体的位置
最后画出点的具体位置,标出名称和角度
先确定
方 向
距离
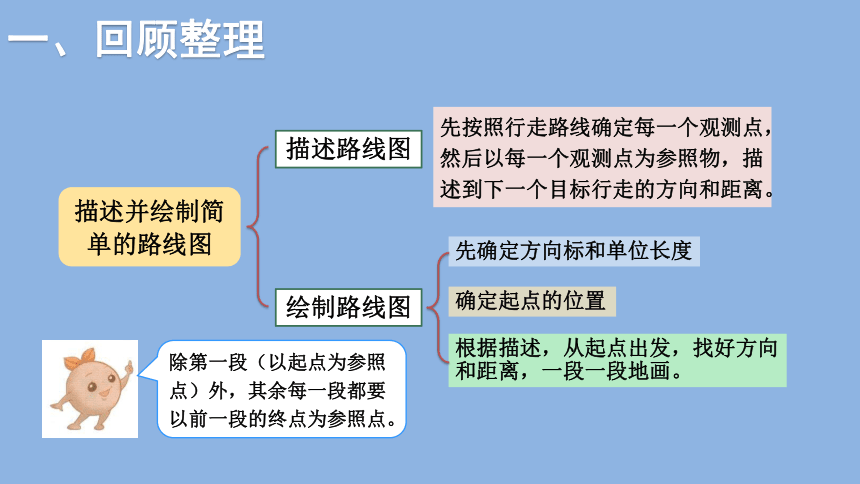
一、回顾整理
描述并绘制简单的路线图
描述路线图
绘制路线图
先按照行走路线确定每一个观测点,然后以每一个观测点为参照物,描述到下一个目标行走的方向和距离。
先确定方向标和单位长度
确定起点的位置
根据描述,从起点出发,找好方向和距离,一段一段地画。
除第一段(以起点为参照点)外,其余每一段都要以前一段的终点为参照点。
一、回顾整理
圆的认识
圆、圆环的面积
圆的周长
想一想,关于圆学了哪些知识?
扇形
一、回顾整理
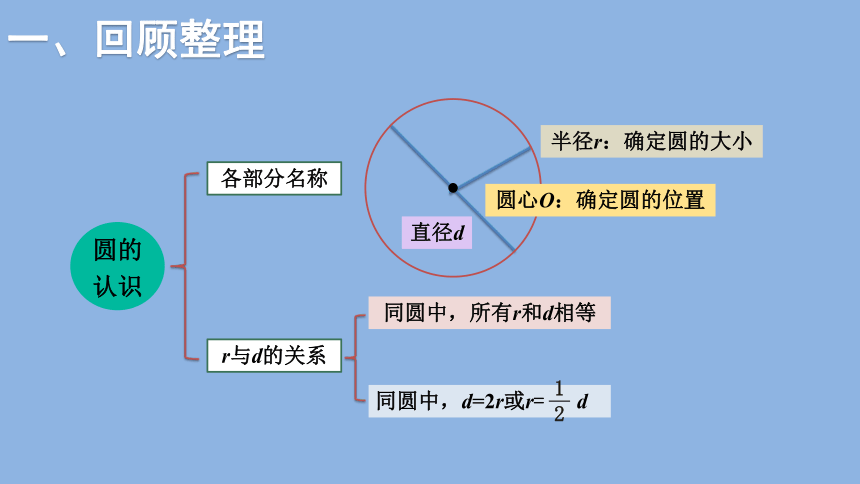
同圆中,所有r和d相等
直径d
圆的认识
各部分名称
r与d的关系
圆心O:确定圆的位置
半径r:确定圆的大小
同圆中,d=2r或r= d
1
2
一、回顾整理
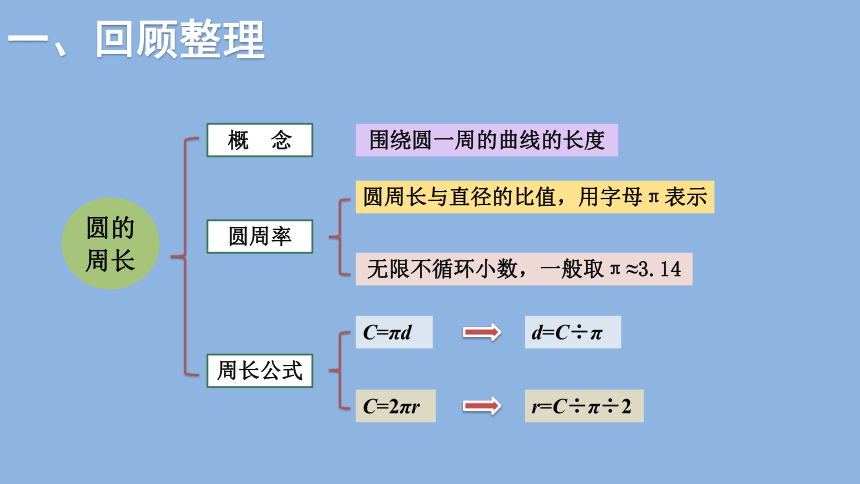
无限不循环小数,一般取π≈3.14
围绕圆一周的曲线的长度
圆周率
周长公式
圆周长与直径的比值,用字母π表示
C=πd
圆的周长
概 念
C=2πr
d=C÷π
r=C÷π÷2
一、回顾整理
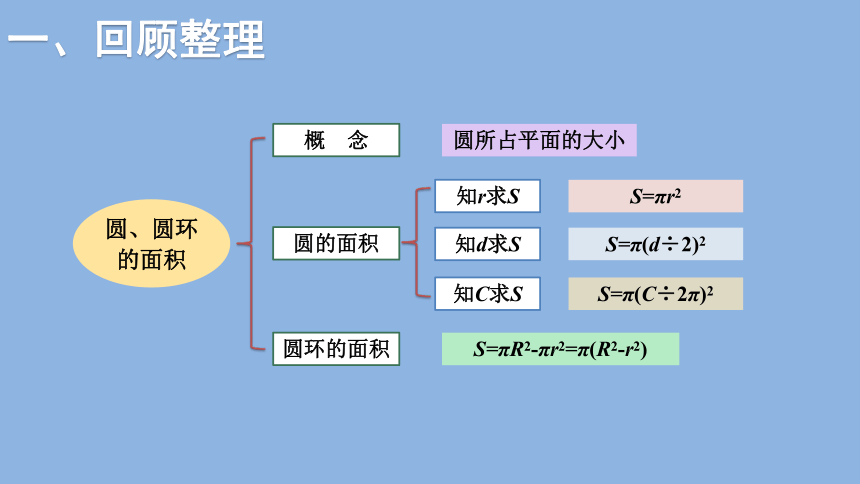
S=πr2
圆所占平面的大小
知r求S
知d求S
S=π(d÷2)2
概 念
S=π(C÷2π)2
知C求S
圆、圆环的面积
圆的面积
圆环的面积
S=πR2-πr2=π(R2-r2)
一、回顾整理
一条弧和经过这条弧两端的半径所围成的图形
概 念
扇形
圆心角
顶点在圆心的角
O
A
B
二、知识应用
4.一个公园是圆形布局,半径长1 km,圆心处设立了一个纪念碑。公园共有四个门,每两个相邻的门之间有一条直的水泥路相通,长约1.41 km。
总复习
(1)这个公园的围墙有多长?
求这个圆形公园的周长
2×3.14×1=6.28(km)
答:这个公园的围墙长6.28 km。
二、知识应用
4.一个公园是圆形布局,半径长1 km,圆心处设立了一个纪念碑。公园共有四个门,每两个相邻的门之间有一条直的水泥路相通,长约1.41 km。
总复习
(2)北门在南门的什么方向?距离南门多远?
北门在南门的正北方,距离南门2 km。
二、知识应用
4.一个公园是圆形布局,半径长1 km,圆心处设立了一个纪念碑。公园共有四个门,每两个相邻的门之间有一条直的水泥路相通,长约1.41 km。
总复习
(3)如果公园里有一个半径为0.2 km的圆形小湖,这个公园的陆地面积是多少平方千米?
3.14×12-3.14×0.22=3.0144(km2)
答:这个公园的陆地面积是3.0144 km2。
二、知识应用
一根绳子的长是37.68 dm,正好绕一棵大树的树干3圈,这棵大树的横截面的周长和面积各是多少?
周长:37.68÷3=12.56(dm)
答:这棵大树的横截面的周长是12.56 dm,面积是12.56 dm2。
知周长求面积
面积:3.14×(12.56÷3.14÷2)2=12.56(dm2)
二、知识应用
在一个直径10 m的圆形水池的周围铺上一条3 m宽的石子小路,这条小路的面积是多少?
答:这条小路的面积是122.46 dm2。
3.14×(10÷2+3)2-3.14×(10÷2)2=122.46(dm2)
三、巩固反馈
14.(1)说一说小动物们居住的位置。
练
习
二
十
三
小猴住在我的……
我要去小鹿家,要先向……
我要去找小熊玩,要走多远呢?
三、巩固反馈
14.(2)请你帮小熊、小象、小鹿解决一下它们提出的问题。
练
习
二
十
三
小猴住在小熊家的南偏东42°方向,距离是400 m。
小象先向南偏西48°方向走300 m到小猴家,再往东走400 m到小鹿家。
小鹿先向西走400 m经过小猴家,然后向北偏西42°走400 m到小熊家。
小猴住在我的……
我要去小鹿家,要先向……
我要去找小熊玩,要走多远呢?
三、巩固反馈
15.写出下面各题的最简单的整数比。
练
习
二
十
三
(1)一个圆的半径和直径的比是_______。
(2)两个圆的半径分别是2 cm和3 cm,它们的直径的比是_____,周长的比是_______,面积的比是_______。
1∶2
2∶3
2∶3
4∶9
三、巩固反馈
16.用三张同样大小的正方形白铁皮(边长1.8m),分别按下面三种方式剪出不同规格的图片。
练
习
二
十
三
图一:3.14×1.8=5.652(m)
图二:3.14×(1.8÷2)=2.826(m)
图三:3.14×(1.8÷3)=1.884(m)
(1)三种圆片的周长分别是多少?
三、巩固反馈
练
习
二
十
三
图一:1.82-3.14×(1.8÷2)2=0.6966(m2)
图二:1.82-3.14×(1.8÷2÷2)2×4=0.6966(m2)
图三:1.82-3.14×(1.8÷3÷2)2×9=0.6966(m2)
(2)剪完圆后,哪张白铁皮剩下的废料多些?
三张白铁皮剩下的废料一样多。
四、课堂小结
通过这节课的复习,你又有哪些收获?
2 图形与几何
一、回顾整理
确定物体位置的条件
描述并绘制简单的路线图
在平面图上确定物体的位置
想一想,关于位置与方向学了哪些知识?
一、回顾整理
确定物体位置的条件
方 向
距 离
用数对确定位置
用方向和距离描述位置时,要找准参照点哦!
再以选定的单位长度确定
一、回顾整理
在平面图上确定物体的位置
最后画出点的具体位置,标出名称和角度
先确定
方 向
距离
一、回顾整理
描述并绘制简单的路线图
描述路线图
绘制路线图
先按照行走路线确定每一个观测点,然后以每一个观测点为参照物,描述到下一个目标行走的方向和距离。
先确定方向标和单位长度
确定起点的位置
根据描述,从起点出发,找好方向和距离,一段一段地画。
除第一段(以起点为参照点)外,其余每一段都要以前一段的终点为参照点。
一、回顾整理
圆的认识
圆、圆环的面积
圆的周长
想一想,关于圆学了哪些知识?
扇形
一、回顾整理
同圆中,所有r和d相等
直径d
圆的认识
各部分名称
r与d的关系
圆心O:确定圆的位置
半径r:确定圆的大小
同圆中,d=2r或r= d
1
2
一、回顾整理
无限不循环小数,一般取π≈3.14
围绕圆一周的曲线的长度
圆周率
周长公式
圆周长与直径的比值,用字母π表示
C=πd
圆的周长
概 念
C=2πr
d=C÷π
r=C÷π÷2
一、回顾整理
S=πr2
圆所占平面的大小
知r求S
知d求S
S=π(d÷2)2
概 念
S=π(C÷2π)2
知C求S
圆、圆环的面积
圆的面积
圆环的面积
S=πR2-πr2=π(R2-r2)
一、回顾整理
一条弧和经过这条弧两端的半径所围成的图形
概 念
扇形
圆心角
顶点在圆心的角
O
A
B
二、知识应用
4.一个公园是圆形布局,半径长1 km,圆心处设立了一个纪念碑。公园共有四个门,每两个相邻的门之间有一条直的水泥路相通,长约1.41 km。
总复习
(1)这个公园的围墙有多长?
求这个圆形公园的周长
2×3.14×1=6.28(km)
答:这个公园的围墙长6.28 km。
二、知识应用
4.一个公园是圆形布局,半径长1 km,圆心处设立了一个纪念碑。公园共有四个门,每两个相邻的门之间有一条直的水泥路相通,长约1.41 km。
总复习
(2)北门在南门的什么方向?距离南门多远?
北门在南门的正北方,距离南门2 km。
二、知识应用
4.一个公园是圆形布局,半径长1 km,圆心处设立了一个纪念碑。公园共有四个门,每两个相邻的门之间有一条直的水泥路相通,长约1.41 km。
总复习
(3)如果公园里有一个半径为0.2 km的圆形小湖,这个公园的陆地面积是多少平方千米?
3.14×12-3.14×0.22=3.0144(km2)
答:这个公园的陆地面积是3.0144 km2。
二、知识应用
一根绳子的长是37.68 dm,正好绕一棵大树的树干3圈,这棵大树的横截面的周长和面积各是多少?
周长:37.68÷3=12.56(dm)
答:这棵大树的横截面的周长是12.56 dm,面积是12.56 dm2。
知周长求面积
面积:3.14×(12.56÷3.14÷2)2=12.56(dm2)
二、知识应用
在一个直径10 m的圆形水池的周围铺上一条3 m宽的石子小路,这条小路的面积是多少?
答:这条小路的面积是122.46 dm2。
3.14×(10÷2+3)2-3.14×(10÷2)2=122.46(dm2)
三、巩固反馈
14.(1)说一说小动物们居住的位置。
练
习
二
十
三
小猴住在我的……
我要去小鹿家,要先向……
我要去找小熊玩,要走多远呢?
三、巩固反馈
14.(2)请你帮小熊、小象、小鹿解决一下它们提出的问题。
练
习
二
十
三
小猴住在小熊家的南偏东42°方向,距离是400 m。
小象先向南偏西48°方向走300 m到小猴家,再往东走400 m到小鹿家。
小鹿先向西走400 m经过小猴家,然后向北偏西42°走400 m到小熊家。
小猴住在我的……
我要去小鹿家,要先向……
我要去找小熊玩,要走多远呢?
三、巩固反馈
15.写出下面各题的最简单的整数比。
练
习
二
十
三
(1)一个圆的半径和直径的比是_______。
(2)两个圆的半径分别是2 cm和3 cm,它们的直径的比是_____,周长的比是_______,面积的比是_______。
1∶2
2∶3
2∶3
4∶9
三、巩固反馈
16.用三张同样大小的正方形白铁皮(边长1.8m),分别按下面三种方式剪出不同规格的图片。
练
习
二
十
三
图一:3.14×1.8=5.652(m)
图二:3.14×(1.8÷2)=2.826(m)
图三:3.14×(1.8÷3)=1.884(m)
(1)三种圆片的周长分别是多少?
三、巩固反馈
练
习
二
十
三
图一:1.82-3.14×(1.8÷2)2=0.6966(m2)
图二:1.82-3.14×(1.8÷2÷2)2×4=0.6966(m2)
图三:1.82-3.14×(1.8÷3÷2)2×9=0.6966(m2)
(2)剪完圆后,哪张白铁皮剩下的废料多些?
三张白铁皮剩下的废料一样多。
四、课堂小结
通过这节课的复习,你又有哪些收获?
