第22章 四边形(一) 单元复习测试-2020-2021学年沪教版(上海)八年级数学下册(机构)(Word版 含答案)
文档属性
| 名称 | 第22章 四边形(一) 单元复习测试-2020-2021学年沪教版(上海)八年级数学下册(机构)(Word版 含答案) | 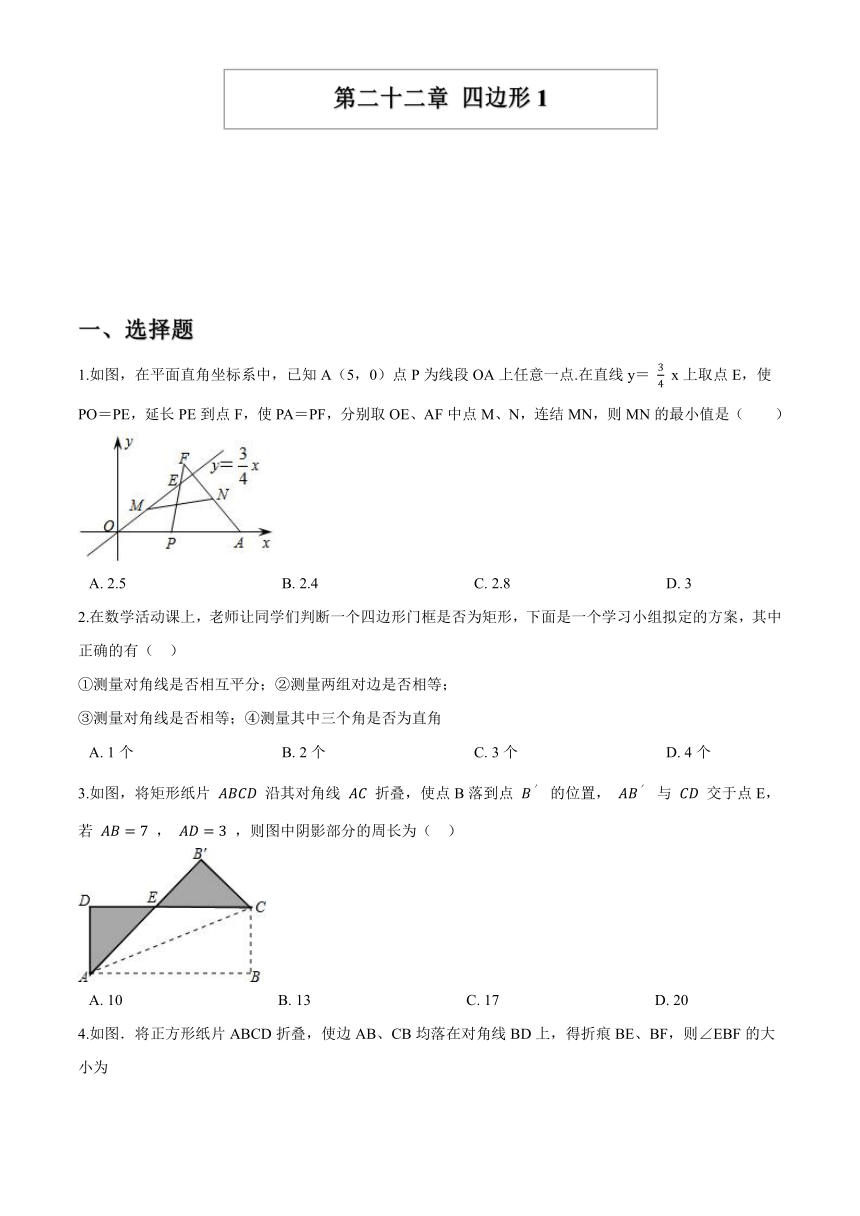 | |
| 格式 | docx | ||
| 文件大小 | 152.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-01 10:50:13 | ||
图片预览



文档简介
1285875-302895第二十二章 四边形1
第二十二章 四边形1
一、选择题
1.如图,在平面直角坐标系中,已知A(5,0)点P为线段OA上任意一点.在直线y= 34 x上取点E,使PO=PE,延长PE到点F,使PA=PF,分别取OE、AF中点M、N,连结MN,则MN的最小值是( )
A.?2.5?????????????????????????????????????????B.?2.4?????????????????????????????????????????C.?2.8?????????????????????????????????????????D.?3
2.在数学活动课上,老师让同学们判断一个四边形门框是否为矩形,下面是一个学习小组拟定的方案,其中正确的有(?? )
①测量对角线是否相互平分;②测量两组对边是否相等;
③测量对角线是否相等;④测量其中三个角是否为直角
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
3.如图,将矩形纸片 ABCD 沿其对角线 AC 折叠,使点B落到点 B′ 的位置, AB′ 与 CD 交于点E,若 AB=7 , AD=3 ,则图中阴影部分的周长为(?? )
A.?10?????????????????????????????????????????B.?13?????????????????????????????????????????C.?17?????????????????????????????????????????D.?20
4.如图.将正方形纸片ABCD折叠,使边AB、CB均落在对角线BD上,得折痕BE、BF,则∠EBF的大小为
A.?15°???????????????????????????????????????B.?30°???????????????????????????????????????C.?45°???????????????????????????????????????D.?60°
5.下列说法正确的是(??? )
A.?有一个角是直角的平行四边形是正方形
B.?对角线互相垂直的矩形是正方形
C.?有一组邻边相等的菱形是正方形
D.?各边都相等的四边形是正方形
6.如图 ∠1,∠2,∠3 是正五边形 ABCDE 的三个外角,若 ∠A+∠B=230°, 则 ∠1+∠2+∠3 =(??? )
A.?140°?????????????????????????????????B.?180°?????????????????????????????????C.?230°?????????????????????????????????D.?320°
7.一个多边形截去一个角后,形成的另一个多边形的内角和是 1620° ,则原来多边形的边数是(??? )
A.?11?????????????????????????????????B.?12?????????????????????????????????C.?11或12?????????????????????????????????D.?10或11或12
8.将一个多边形纸片剪去一个内角后得到一个内角和是外角和4倍的新多边形,则原多边形的边数为(??? )
A.?9????????????????????????????????????B.?10????????????????????????????????????C.?11????????????????????????????????????D.?以上均有可能
9.如图,已知在正方形ABCD中,E是BC上一点,将正方形的边CD沿DE折叠到DF,延长EF交AB于点G,连接DG.现有如下4个结论:①AG=GF;②AG与EC一定不相等;③ ∠GDE=45° ;④ △BGE 的周长是一个定值.其中正确的个数为(??? )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
10.如图,四边形ABCD是平行四边形,下列说法能判定四边形ABCD是菱形的是(?? )
A.?AC⊥BD????????????????????????????B.?BA⊥BD????????????????????????????C.?AB=CD????????????????????????????D.?AD=BC
二、填空题
11.如图1,直角三角形纸片的一条直角边长为1,斜边为3,把它们按图2,拼摆正方形,纸片在结合部分不重叠无缝隙,则图2的中间空白部分,即四边形 ABCD 的面积为________.
12.如图,将5个大小相同的正方形置于平面直角坐标系中,若顶点 M , N 的标分別为 (2,6) 、 (8,6) ,则顶点 A 的坐标为________;
13.如图,在菱形 ABCD 中,O是对角线 BD 上一点, ⊙O 经过点A,B,C,若 ⊙O 的半径为2, OD=4 ,则 BC 的长为________.
14.如图,在四边形 ABCD 中, ∠ABC=150° , BD 平分 ∠ABC ,过 A 点作 AE//BC 交 BD 于点 E , EF⊥BC 于点 F 若 AB=6 ,则 EF 的长为________.
三、计算与解答
15.如图,菱形 ABCD 的对角线 AC 与 BD 相交于 O , E 是 BC 中点,连接 OE 并延长到 F ,使 EF=OE .求证:四边形 OBFC 是矩形.
16.如图A、B是 ⊙O 上的两点, ∠AOB=120? ,C是弧 AB 的中点,求证四边形 OACB 是菱形.
17.一个多边形的内角和是它外角和的两倍,那么它是多少边形?
18.在平面直角坐标系中,己知O为坐标原点,点 BC∩A1B=B ,以点A为旋转中心,把 △ABO 顺时针旋转,得 △ACD .
(Ⅰ)如图①,当旋转后满足 DC//x 轴时,求点C的坐标.
(Ⅱ)如图②,当旋转后点C恰好落在x轴正半轴上时,求点D的坐标.
(Ⅲ)在(Ⅱ)的条件下,边 OB 上的一点P旋转后的对应点为 P′ ,当 DP+AP′ 取得最小值时,求点P的坐标(直接写出结果即可)
参考答案
1.【答案】 B 2.【答案】 C 3.【答案】 D 4.【答案】 C 5.【答案】 B 6.【答案】 C 7.【答案】 D 8.【答案】 D 9.【答案】 C 10.【答案】 A
11.【答案】 9?42 12.【答案】 (10,2) 13.【答案】 23 14.【答案】 3
15.【答案】 证明:∵ E 是 BC 中点,∴ BE=CE ,
∵ EF=OE ,
∴四边形 OBFC 是平行四边形,
∵ 四边形 ABCD 是菱形,
∴ AC⊥BD ,
∴ ∠BOC=90° ,
∴平行四边形 OBFC 是矩形.
16.【答案】 证明:连 OC ,如图,
∵C是 AB 的中点, ∠AOB=120?
∴ ∠AOC=∠BOC=60? ,
又∵ OA =OC=OB ,
∴ △OAC 和 △OBC 都是等边三角形,
∴ AC=OA=OB=BC ,
∴四边形OACB是菱形.
17.【答案】 解:设这个多边形是n边形,依根据题意得:
(n-2)?180°=2×360°,
解得n=6.
∴它是六边形.
18.【答案】 解:(Ⅰ)如图①中,作 CH⊥x 轴于H.
∵ CD//AH,∠D=∠AHC=90° ,
∴ ∠DAH=90° ,
∴四边形 ADCH 是矩形,
∴ AD=OA=CH=2,CD=OB=AH=4 ,
∴ OH=6 ,
∴ C(6,2)
(Ⅱ)如图②中,作 DK⊥AC 于K.
在 Rt△ADC 中,∵ AD=2,CD=4 ,
∴ AC=25 ,
∵ 12?AD?DC=12?AC?DK ,
∴ DK=455,AK=255 ,
∴ OK=2+255 ,
∴ D(2+255,455)
(Ⅲ)如图③中,连接PA、AP′,作点A关于y轴的对称点A′,连接DA′交y轴于P′,连接AP′.
由题意PA=AP′,
∴AP′+PD=PA+PD,
根据两点之间线段最短,可知当点P与点P′重合时,PA+PD的值最小.
∵A′(?2,0),D(2+255,455) ,
∴直线A′D的解析式为 y=45?219x+85?419 ,
点P坐标 (0,85?419)
第二十二章 四边形1
一、选择题
1.如图,在平面直角坐标系中,已知A(5,0)点P为线段OA上任意一点.在直线y= 34 x上取点E,使PO=PE,延长PE到点F,使PA=PF,分别取OE、AF中点M、N,连结MN,则MN的最小值是( )
A.?2.5?????????????????????????????????????????B.?2.4?????????????????????????????????????????C.?2.8?????????????????????????????????????????D.?3
2.在数学活动课上,老师让同学们判断一个四边形门框是否为矩形,下面是一个学习小组拟定的方案,其中正确的有(?? )
①测量对角线是否相互平分;②测量两组对边是否相等;
③测量对角线是否相等;④测量其中三个角是否为直角
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
3.如图,将矩形纸片 ABCD 沿其对角线 AC 折叠,使点B落到点 B′ 的位置, AB′ 与 CD 交于点E,若 AB=7 , AD=3 ,则图中阴影部分的周长为(?? )
A.?10?????????????????????????????????????????B.?13?????????????????????????????????????????C.?17?????????????????????????????????????????D.?20
4.如图.将正方形纸片ABCD折叠,使边AB、CB均落在对角线BD上,得折痕BE、BF,则∠EBF的大小为
A.?15°???????????????????????????????????????B.?30°???????????????????????????????????????C.?45°???????????????????????????????????????D.?60°
5.下列说法正确的是(??? )
A.?有一个角是直角的平行四边形是正方形
B.?对角线互相垂直的矩形是正方形
C.?有一组邻边相等的菱形是正方形
D.?各边都相等的四边形是正方形
6.如图 ∠1,∠2,∠3 是正五边形 ABCDE 的三个外角,若 ∠A+∠B=230°, 则 ∠1+∠2+∠3 =(??? )
A.?140°?????????????????????????????????B.?180°?????????????????????????????????C.?230°?????????????????????????????????D.?320°
7.一个多边形截去一个角后,形成的另一个多边形的内角和是 1620° ,则原来多边形的边数是(??? )
A.?11?????????????????????????????????B.?12?????????????????????????????????C.?11或12?????????????????????????????????D.?10或11或12
8.将一个多边形纸片剪去一个内角后得到一个内角和是外角和4倍的新多边形,则原多边形的边数为(??? )
A.?9????????????????????????????????????B.?10????????????????????????????????????C.?11????????????????????????????????????D.?以上均有可能
9.如图,已知在正方形ABCD中,E是BC上一点,将正方形的边CD沿DE折叠到DF,延长EF交AB于点G,连接DG.现有如下4个结论:①AG=GF;②AG与EC一定不相等;③ ∠GDE=45° ;④ △BGE 的周长是一个定值.其中正确的个数为(??? )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
10.如图,四边形ABCD是平行四边形,下列说法能判定四边形ABCD是菱形的是(?? )
A.?AC⊥BD????????????????????????????B.?BA⊥BD????????????????????????????C.?AB=CD????????????????????????????D.?AD=BC
二、填空题
11.如图1,直角三角形纸片的一条直角边长为1,斜边为3,把它们按图2,拼摆正方形,纸片在结合部分不重叠无缝隙,则图2的中间空白部分,即四边形 ABCD 的面积为________.
12.如图,将5个大小相同的正方形置于平面直角坐标系中,若顶点 M , N 的标分別为 (2,6) 、 (8,6) ,则顶点 A 的坐标为________;
13.如图,在菱形 ABCD 中,O是对角线 BD 上一点, ⊙O 经过点A,B,C,若 ⊙O 的半径为2, OD=4 ,则 BC 的长为________.
14.如图,在四边形 ABCD 中, ∠ABC=150° , BD 平分 ∠ABC ,过 A 点作 AE//BC 交 BD 于点 E , EF⊥BC 于点 F 若 AB=6 ,则 EF 的长为________.
三、计算与解答
15.如图,菱形 ABCD 的对角线 AC 与 BD 相交于 O , E 是 BC 中点,连接 OE 并延长到 F ,使 EF=OE .求证:四边形 OBFC 是矩形.
16.如图A、B是 ⊙O 上的两点, ∠AOB=120? ,C是弧 AB 的中点,求证四边形 OACB 是菱形.
17.一个多边形的内角和是它外角和的两倍,那么它是多少边形?
18.在平面直角坐标系中,己知O为坐标原点,点 BC∩A1B=B ,以点A为旋转中心,把 △ABO 顺时针旋转,得 △ACD .
(Ⅰ)如图①,当旋转后满足 DC//x 轴时,求点C的坐标.
(Ⅱ)如图②,当旋转后点C恰好落在x轴正半轴上时,求点D的坐标.
(Ⅲ)在(Ⅱ)的条件下,边 OB 上的一点P旋转后的对应点为 P′ ,当 DP+AP′ 取得最小值时,求点P的坐标(直接写出结果即可)
参考答案
1.【答案】 B 2.【答案】 C 3.【答案】 D 4.【答案】 C 5.【答案】 B 6.【答案】 C 7.【答案】 D 8.【答案】 D 9.【答案】 C 10.【答案】 A
11.【答案】 9?42 12.【答案】 (10,2) 13.【答案】 23 14.【答案】 3
15.【答案】 证明:∵ E 是 BC 中点,∴ BE=CE ,
∵ EF=OE ,
∴四边形 OBFC 是平行四边形,
∵ 四边形 ABCD 是菱形,
∴ AC⊥BD ,
∴ ∠BOC=90° ,
∴平行四边形 OBFC 是矩形.
16.【答案】 证明:连 OC ,如图,
∵C是 AB 的中点, ∠AOB=120?
∴ ∠AOC=∠BOC=60? ,
又∵ OA =OC=OB ,
∴ △OAC 和 △OBC 都是等边三角形,
∴ AC=OA=OB=BC ,
∴四边形OACB是菱形.
17.【答案】 解:设这个多边形是n边形,依根据题意得:
(n-2)?180°=2×360°,
解得n=6.
∴它是六边形.
18.【答案】 解:(Ⅰ)如图①中,作 CH⊥x 轴于H.
∵ CD//AH,∠D=∠AHC=90° ,
∴ ∠DAH=90° ,
∴四边形 ADCH 是矩形,
∴ AD=OA=CH=2,CD=OB=AH=4 ,
∴ OH=6 ,
∴ C(6,2)
(Ⅱ)如图②中,作 DK⊥AC 于K.
在 Rt△ADC 中,∵ AD=2,CD=4 ,
∴ AC=25 ,
∵ 12?AD?DC=12?AC?DK ,
∴ DK=455,AK=255 ,
∴ OK=2+255 ,
∴ D(2+255,455)
(Ⅲ)如图③中,连接PA、AP′,作点A关于y轴的对称点A′,连接DA′交y轴于P′,连接AP′.
由题意PA=AP′,
∴AP′+PD=PA+PD,
根据两点之间线段最短,可知当点P与点P′重合时,PA+PD的值最小.
∵A′(?2,0),D(2+255,455) ,
∴直线A′D的解析式为 y=45?219x+85?419 ,
点P坐标 (0,85?419)
