第22章 四边形(二) 单元复习测试-2020-2021学年沪教版(上海)八年级数学下册(机构)(Word版 含答案)
文档属性
| 名称 | 第22章 四边形(二) 单元复习测试-2020-2021学年沪教版(上海)八年级数学下册(机构)(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 141.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-01 10:58:24 | ||
图片预览

文档简介
1285875-302895第二十二章 四边形2
第二十二章 四边形2
一、选择题
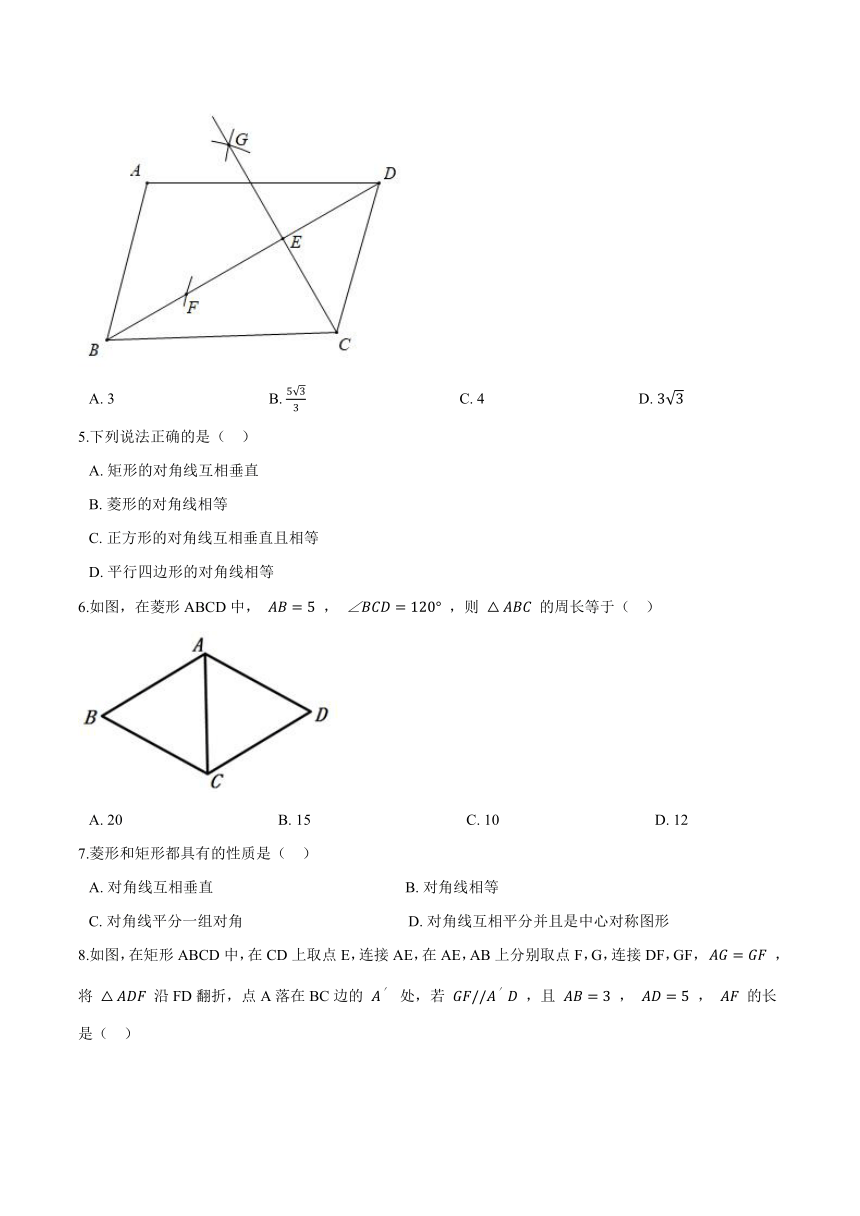
1.如图,在平面直角坐标系中,四边形OABC是矩形,点O是坐标原点,点A、C的坐标分别是 (6,0) , (0,3) ,点B在第一象限,则点B的坐标是(?? )
A.?(3,6)???????????????????????????????????B.?(6,3)???????????????????????????????????C.?(6,6)???????????????????????????????????D.?(3,3)
2.平行四边形、矩形、菱形、正方形共有的性质是(?? ).
A.?对角线互相平分?????????????B.?对角线相等?????????????C.?对角线互相垂直?????????????D.?对角形互相垂直平分
3.如图所示,反比例函数 y=kx ( k≠0 , x≥0 )的图象经过矩形OABC的对角线AC的中点D.若矩形OABC的面积为等于8,则k的值等于(?? )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
4.如图,在 ?ABCD 中, AD=6 , ∠ADB=30° ,按以下步骤作图:①以点 C 为圆心,以 CD 长为半径作弧,交 BD 于点 F ;②分别以点 D , F 为圆心,以 CD 长为半径作弧,两弧相交于点 G ,作射线 CG 交 BD 于点 E ,则 BE 的长为(?? )
A.?3????????????????????????????????????????B.?533????????????????????????????????????????C.?4????????????????????????????????????????D.?33
5.下列说法正确的是(?? )
A.?矩形的对角线互相垂直
B.?菱形的对角线相等
C.?正方形的对角线互相垂直且相等
D.?平行四边形的对角线相等
6.如图,在菱形ABCD中, AB=5 , ∠BCD=120° ,则 △ABC 的周长等于(?? )
A.?20?????????????????????????????????????????B.?15?????????????????????????????????????????C.?10?????????????????????????????????????????D.?12
7.菱形和矩形都具有的性质是(?? )
A.?对角线互相垂直??????????????????????????????????????????????????B.?对角线相等
C.?对角线平分一组对角???????????????????????????????????????????D.?对角线互相平分并且是中心对称图形
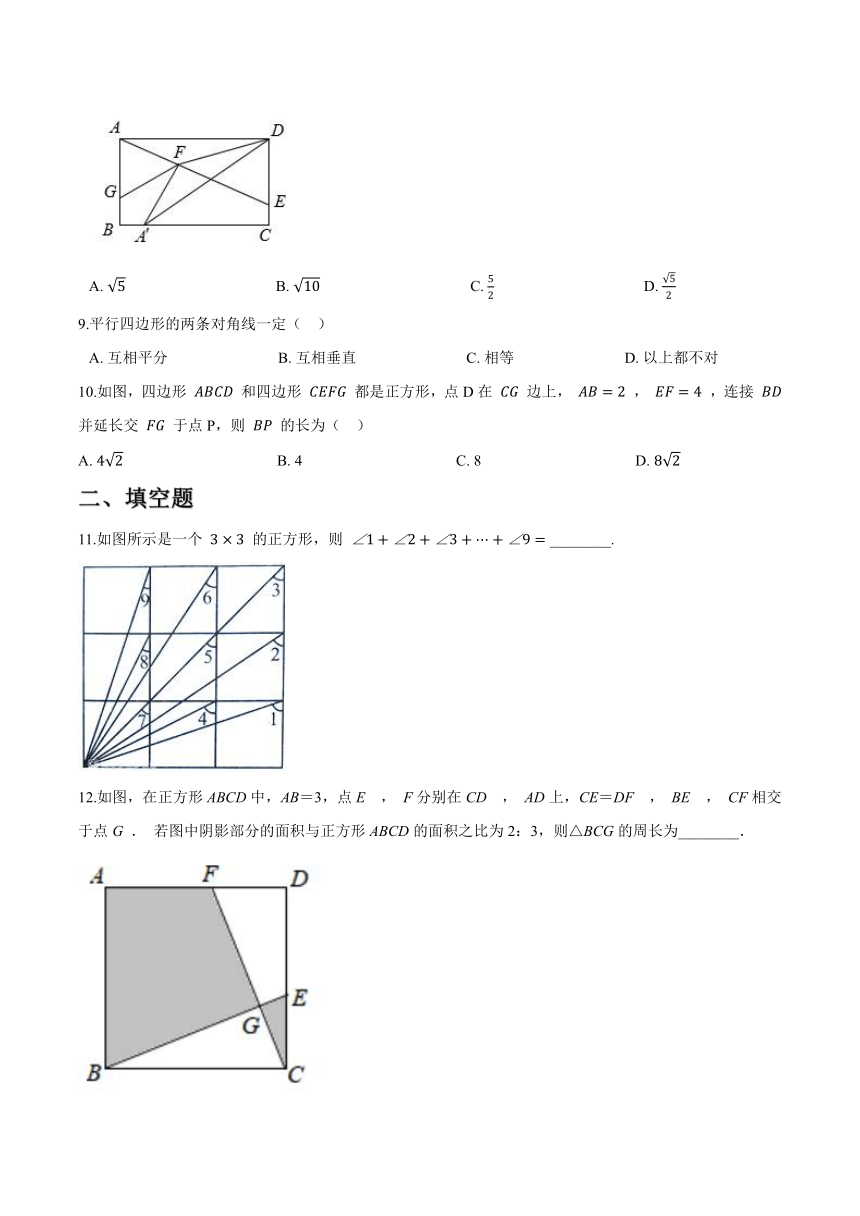
8.如图,在矩形ABCD中,在CD上取点E,连接AE,在AE,AB上分别取点F,G,连接DF,GF, AG=GF ,将 △ADF 沿FD翻折,点A落在BC边的 A′ 处,若 GF//A′D ,且 AB=3 , AD=5 , AF 的长是(?? )
A.?5???????????????????????????????????????B.?10???????????????????????????????????????C.?52???????????????????????????????????????D.?52
9.平行四边形的两条对角线一定(?? )
A.?互相平分?????????????????????????????B.?互相垂直?????????????????????????????C.?相等?????????????????????????????D.?以上都不对
10.如图,四边形 ABCD 和四边形 CEFG 都是正方形,点D在 CG 边上, AB=2 , EF=4 ,连接 BD 并延长交 FG 于点P,则 BP 的长为(?? )A.?42????????????????????????????????????????B.?4????????????????????????????????????????C.?8????????????????????????????????????????D.?82
二、填空题
11.如图所示是一个 3×3 的正方形,则 ∠1+∠2+∠3+?+∠9= ________.
12.如图,在正方形ABCD中,AB=3,点E , F分别在CD , AD上,CE=DF , BE , CF相交于点G . 若图中阴影部分的面积与正方形ABCD的面积之比为2:3,则△BCG的周长为________.
13.如图,对折矩形ABCD,使AB与DC重合,得到折痕EF,将纸片展平再一次折叠,使点D落到G,并使折痕经过点A,已知BC=2.则线段EG的长度为________.
14.如图,已知矩形 ABCD , AB=6 , BC=4 ,点E在 AD 上,连接 EC ,将四边形 ABCE 沿 CE 折叠,得到四边形 A′B′CE ,且 A′B′ 刚好经过点D,则 △CDE 的面积为________.
三、计算与解答
15.如图,在等边△ABC中,点D是AC的中点,点F是BC的中点,以BD为边作等边△BDE , 连结点A、E . 求证:四边形AEBF为矩形.
16.如图是一个凹多边形, ∠A=90? , ∠C=106? , ∠D=119? , ∠E=100? ;求 ∠1+∠2 的值.
17.如图,在平行四边形ABCD中,AB⊥BD , M、N分别为边AD与BC的中点.
求证:四边形BMDN是菱形.
18.如图,两张等宽的纸条交叉重叠在一起,重叠的部分ABCD是菱形吗?为什么?
参考答案
1.【答案】 B 2.【答案】 A 3.【答案】 B 4.【答案】 D 5.【答案】 C 6.【答案】 B 7.【答案】 D 8.【答案】 A 9.【答案】 A 10.【答案】 A
11.【答案】 405° 12.【答案】 15+3 13.【答案】 3 14.【答案】 27?95
15.【答案】 证明:∵在等边△ABC中,点D是AC的中点,点F是BC的中点,
∴AB = BC,∠ADB = ∠AFB= 90°,∠DBC=30°,
∠BAD = ∠ABF = 60°
∴△ABF≌△ABD,
∴BD = AF.
∵△BDE是等边三角形,
∴BD = BE,∠EBD = 60°.
∴AF = BE,∠EBF = ∠EBD + ∠DBC = 90°.
∴∠AFC = ∠EBF.
∴AF∥BE.
∴四边形AEBF是平行四边形.
∵∠EBF=90°,
∴平行四边形AEBF是矩形.
16.【答案】 证明:连接 BF
∵ ∠A=90? ,
∴ ∠AFB+∠ABF=90° ?,
∵ ∠E+∠D+∠C+∠FBC+∠EFB=(5?2)?180°=540° ,
∠C=106? , ∠D=119? , ∠E=100? ,
∴ ∠1+∠2=540??100??119??106??90?=125? .
17.【答案】 证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
又∵M、N是AD、BC的中点,
∴MD∥BN,MD=BN.
∴四边形BNMD是平行四边形.
又∵AB⊥BD,
∴MD=BM,
∴四边形BNMD是菱形.
18.【答案】 依题意可知AB∥CD,AD∥BC.
∴四边形ABCD是平行四边形.
分别作CD,BC边上的高为AE,AF,
∵两纸条相同,所以纸条宽度AE=AF.
∵平行四边形的面积为AE×CD=BC×AF,
∴CD=BC.
∴平行四边形ABCD为菱形;
第二十二章 四边形2
一、选择题
1.如图,在平面直角坐标系中,四边形OABC是矩形,点O是坐标原点,点A、C的坐标分别是 (6,0) , (0,3) ,点B在第一象限,则点B的坐标是(?? )
A.?(3,6)???????????????????????????????????B.?(6,3)???????????????????????????????????C.?(6,6)???????????????????????????????????D.?(3,3)
2.平行四边形、矩形、菱形、正方形共有的性质是(?? ).
A.?对角线互相平分?????????????B.?对角线相等?????????????C.?对角线互相垂直?????????????D.?对角形互相垂直平分
3.如图所示,反比例函数 y=kx ( k≠0 , x≥0 )的图象经过矩形OABC的对角线AC的中点D.若矩形OABC的面积为等于8,则k的值等于(?? )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
4.如图,在 ?ABCD 中, AD=6 , ∠ADB=30° ,按以下步骤作图:①以点 C 为圆心,以 CD 长为半径作弧,交 BD 于点 F ;②分别以点 D , F 为圆心,以 CD 长为半径作弧,两弧相交于点 G ,作射线 CG 交 BD 于点 E ,则 BE 的长为(?? )
A.?3????????????????????????????????????????B.?533????????????????????????????????????????C.?4????????????????????????????????????????D.?33
5.下列说法正确的是(?? )
A.?矩形的对角线互相垂直
B.?菱形的对角线相等
C.?正方形的对角线互相垂直且相等
D.?平行四边形的对角线相等
6.如图,在菱形ABCD中, AB=5 , ∠BCD=120° ,则 △ABC 的周长等于(?? )
A.?20?????????????????????????????????????????B.?15?????????????????????????????????????????C.?10?????????????????????????????????????????D.?12
7.菱形和矩形都具有的性质是(?? )
A.?对角线互相垂直??????????????????????????????????????????????????B.?对角线相等
C.?对角线平分一组对角???????????????????????????????????????????D.?对角线互相平分并且是中心对称图形
8.如图,在矩形ABCD中,在CD上取点E,连接AE,在AE,AB上分别取点F,G,连接DF,GF, AG=GF ,将 △ADF 沿FD翻折,点A落在BC边的 A′ 处,若 GF//A′D ,且 AB=3 , AD=5 , AF 的长是(?? )
A.?5???????????????????????????????????????B.?10???????????????????????????????????????C.?52???????????????????????????????????????D.?52
9.平行四边形的两条对角线一定(?? )
A.?互相平分?????????????????????????????B.?互相垂直?????????????????????????????C.?相等?????????????????????????????D.?以上都不对
10.如图,四边形 ABCD 和四边形 CEFG 都是正方形,点D在 CG 边上, AB=2 , EF=4 ,连接 BD 并延长交 FG 于点P,则 BP 的长为(?? )A.?42????????????????????????????????????????B.?4????????????????????????????????????????C.?8????????????????????????????????????????D.?82
二、填空题
11.如图所示是一个 3×3 的正方形,则 ∠1+∠2+∠3+?+∠9= ________.
12.如图,在正方形ABCD中,AB=3,点E , F分别在CD , AD上,CE=DF , BE , CF相交于点G . 若图中阴影部分的面积与正方形ABCD的面积之比为2:3,则△BCG的周长为________.
13.如图,对折矩形ABCD,使AB与DC重合,得到折痕EF,将纸片展平再一次折叠,使点D落到G,并使折痕经过点A,已知BC=2.则线段EG的长度为________.
14.如图,已知矩形 ABCD , AB=6 , BC=4 ,点E在 AD 上,连接 EC ,将四边形 ABCE 沿 CE 折叠,得到四边形 A′B′CE ,且 A′B′ 刚好经过点D,则 △CDE 的面积为________.
三、计算与解答
15.如图,在等边△ABC中,点D是AC的中点,点F是BC的中点,以BD为边作等边△BDE , 连结点A、E . 求证:四边形AEBF为矩形.
16.如图是一个凹多边形, ∠A=90? , ∠C=106? , ∠D=119? , ∠E=100? ;求 ∠1+∠2 的值.
17.如图,在平行四边形ABCD中,AB⊥BD , M、N分别为边AD与BC的中点.
求证:四边形BMDN是菱形.
18.如图,两张等宽的纸条交叉重叠在一起,重叠的部分ABCD是菱形吗?为什么?
参考答案
1.【答案】 B 2.【答案】 A 3.【答案】 B 4.【答案】 D 5.【答案】 C 6.【答案】 B 7.【答案】 D 8.【答案】 A 9.【答案】 A 10.【答案】 A
11.【答案】 405° 12.【答案】 15+3 13.【答案】 3 14.【答案】 27?95
15.【答案】 证明:∵在等边△ABC中,点D是AC的中点,点F是BC的中点,
∴AB = BC,∠ADB = ∠AFB= 90°,∠DBC=30°,
∠BAD = ∠ABF = 60°
∴△ABF≌△ABD,
∴BD = AF.
∵△BDE是等边三角形,
∴BD = BE,∠EBD = 60°.
∴AF = BE,∠EBF = ∠EBD + ∠DBC = 90°.
∴∠AFC = ∠EBF.
∴AF∥BE.
∴四边形AEBF是平行四边形.
∵∠EBF=90°,
∴平行四边形AEBF是矩形.
16.【答案】 证明:连接 BF
∵ ∠A=90? ,
∴ ∠AFB+∠ABF=90° ?,
∵ ∠E+∠D+∠C+∠FBC+∠EFB=(5?2)?180°=540° ,
∠C=106? , ∠D=119? , ∠E=100? ,
∴ ∠1+∠2=540??100??119??106??90?=125? .
17.【答案】 证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
又∵M、N是AD、BC的中点,
∴MD∥BN,MD=BN.
∴四边形BNMD是平行四边形.
又∵AB⊥BD,
∴MD=BM,
∴四边形BNMD是菱形.
18.【答案】 依题意可知AB∥CD,AD∥BC.
∴四边形ABCD是平行四边形.
分别作CD,BC边上的高为AE,AF,
∵两纸条相同,所以纸条宽度AE=AF.
∵平行四边形的面积为AE×CD=BC×AF,
∴CD=BC.
∴平行四边形ABCD为菱形;
