20.3一次函数的应用 讲义-2020-2021学年沪教版(上海)八年级数学下册(机构)(含答案)
文档属性
| 名称 | 20.3一次函数的应用 讲义-2020-2021学年沪教版(上海)八年级数学下册(机构)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 142.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-01 00:00:00 | ||
图片预览



文档简介
1285875-30289520.3一次函数的应用
20.3一次函数的应用
学习目标
1.能用函数的观点认识一次函数、一次方程(组)与一元一次不等式之间的联系,能直观地用图形(在平面直角坐标系中)来表示方程(或方程组)的解及不等式的解,建立数形结合的思想及转化的思想.
2.能运用一次函数的性质解决简单的不等式问题及实际问题.
要点梳理
要点1
一元一次方程与一次函数
对于一次函数false,由它的函数值false就得到关于false的一元一次方程false,解这个方程得false,于是可以知道一次函数false的图像与false轴的交点坐标为false.
若已知一次函数false的图像与false轴的交点坐标,也可以知道这个交点的横坐标false,其就是一元一次方程false的根.
要点2一元一次不等式与一次函数
由一次函数false的函数值false大于0(或小于0),就得到关于false的一元一次不等式false(或false)的解集.
在一次函数false的图像上且位于false轴上方(或下方)的所有点,它们的横坐标的取值范围就是不等式false(或false)的解集.
典型例题
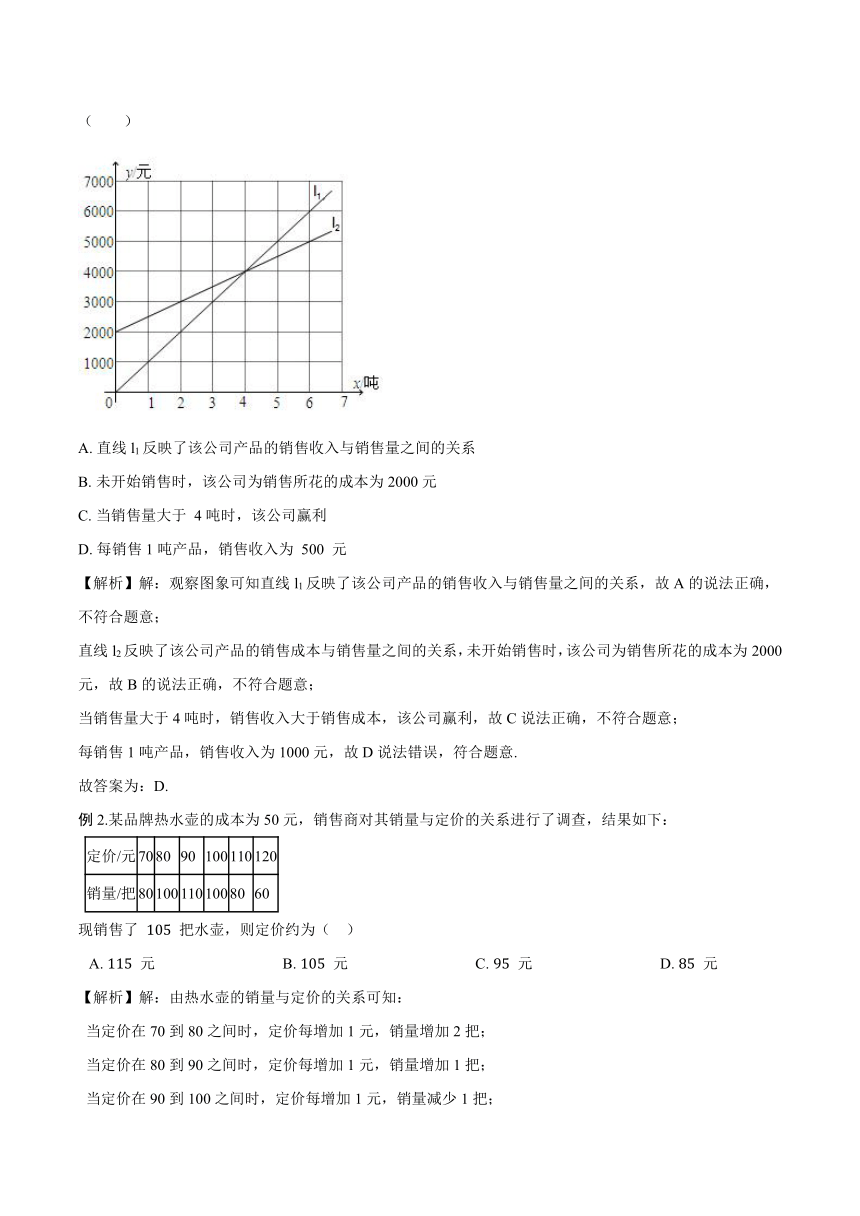
例1.如图所示直线反映了某公司产品的销售成本和销售收入与销售量之间的关系,则下列说法错误的是( )
A.?直线l1反映了该公司产品的销售收入与销售量之间的关系
B.?未开始销售时,该公司为销售所花的成本为2000元
C.?当销售量大于 4吨时,该公司赢利
D.?每销售1吨产品,销售收入为 500 元
【解析】解:观察图象可知直线l1反映了该公司产品的销售收入与销售量之间的关系,故A的说法正确,不符合题意;
直线l2反映了该公司产品的销售成本与销售量之间的关系,未开始销售时,该公司为销售所花的成本为2000元,故B的说法正确,不符合题意;
当销售量大于4吨时,销售收入大于销售成本,该公司赢利,故C说法正确,不符合题意;
每销售1吨产品,销售收入为1000元,故D说法错误,符合题意.
故答案为:D.
例2.某品牌热水壶的成本为50元,销售商对其销量与定价的关系进行了调查,结果如下:
定价/元
70
80
90
100
110
120
销量/把
80
100
110
100
80
60
现销售了 105 把水壶,则定价约为(?? )
A.?115 元?????????????????????????????????B.?105 元?????????????????????????????????C.?95 元?????????????????????????????????D.?85 元
【解析】解:由热水壶的销量与定价的关系可知:
当定价在70到80之间时,定价每增加1元,销量增加2把;
当定价在80到90之间时,定价每增加1元,销量增加1把;
当定价在90到100之间时,定价每增加1元,销量减少1把;
当定价在100到110之间时,定价每增加1元,销量减少2把;
当定价在110到120之间时,定价每增加1元,销量减少2把;
∵100<105<110
由表格可知定价约为
80+(105-100)÷1=80+5=85.
∴定价约为85元.
故答案为:D.
基础巩固
1.港口 A,B,C 依次在同一条直线上,甲、乙两艘船同时分别从 A,B 两港出发,匀速驶向 C 港,甲、乙两船与 B 港的距离 y (海里)与行驶时间 x (小时)之间的函数关系如图所示,则下列说法正确的有(? )
① B,C 两港之间的距离为60海里
②甲、乙两船在途中只相遇了一次
③甲船平均速度比乙船平均速度快30海里/时
④甲船到达 C 港时,乙船还需要一个小时才到达 C 港
⑤点 P 的坐标为 (1,30)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
2.甲、乙两车同时从A地出发,沿同一路线各自匀速向B地行驶,甲到达B地停留1小时后按原路以另一速度匀速返回,直到与乙车相遇.乙车的速度为每小时60千米.两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示,则下列结论错误的是(??? )
A.?行驶3小时后,两车相距120千米????????????????????????B.?甲车从A到B的速度为100千米/小时
C.?甲车返回是行驶的速度为95千米/小时????????????????D.?A,B两地之间的距离为300千米
3.一根蜡烛长20cm , 点燃后每小时燃烧5cm燃烧时剩下的高度h(cm)与时间t(小时)的关系图象表示是( )
A.???????????????B.???????????????C.???????????????D.?
4.甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(单位:km)与甲车行驶时间x(单位:h)之间的函数关系如图所示,根据图象提供的信息,下列结论错误的是(????? )
A.?两城相距480千米???????????????????????????????????????????????B.?乙车比甲车晚出发1小时,却早到1小时
C.?当乙车到达B城时,甲车距离B城80千米?????????????D.?甲车出发后4小时,乙车追上甲车
5.弹簧挂上物体后会伸长,测得一弹簧的长度y (cm)与所挂的物体的质量x(kg)之间有下面的关系:
x/kg
0
1
2
3
4
5
y/cm
10
10.5
11
11.5
12
12.5
下列说法错误的是(???? )
A.?x与y都是变量,且x是自变量,y是因变量???????????B.?弹簧不挂重物时的长度为0 cm
C.?物体质量每增加1 kg,弹簧长度y增加0.5 cm??????D.?所挂物体质量为7 kg时,弹簧长度为13.5 cm
6.在运动会径赛中,甲、乙两人同时起跑,刚跑出200米甲不慎摔倒,他又迅速地爬起来继续投入比赛.他们所跑的路程 y(m) 与比赛时间 x(s) 的关系如图,有下列说法:
①他们进行的是 800m 比赛; ②乙全程的平均速度为 6.4m/s ③甲摔倒之前,乙的速度快:④甲再次投入比赛后的平均速度为 7.5m/s ;⑤甲再次投入比赛后在距离终点300米时追上了乙其中正确的个数有(?? )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
7.甲、乙两车分别从A、B两地同时出发,相向行驶,已知甲车的速度大于乙车的速度,甲车到达B地后马上以另一速度原路返回A地(掉头的时间忽略不计),乙车到达A地以后即停在地等待甲车.如图所示为甲乙两车间的距离y(千米)与甲车的行驶时间t(小时)之间的函数图象,则当乙车到达A地的时候,甲车与A地的距离为________千米.
8.声音在空气中的传播速度 v(ms) 与温度 t(℃) 的关系如表:
温度(℃)
0
5
10
15
20
速度 v(ms)
331
336
341
346
351
若声音在空气中的传播速度 v(ms) 是温度 t(℃) 的一次函数;当 t=25℃ 时,声音的传播速度为________ ms .
9.今年10月1日上午,庆祝中华人民共和国成立70周年阅兵式在天安门正式举行.通常提到的“阅兵”,实际是分为“阅兵式”和“分列式”.阅兵式,就是士兵不动,军委主席坐车来检阅.分列式,就是所有方(梯)队,踏着统一的节奏,依次通过天安门前检阅区.在分列式中,受检阅的距离就是天安门前,东西的两个华表之间,两个华表相隔 96 米.受检阅官兵迈着每步 75 厘米,必需x步走完,若步速每分钟 122 步,需要时间y秒.求出x与y各是多少?若淮北籍东海舰队航空兵副司令员梁旭少将在受检阅时,他走过的路程s步,行走的时间为t秒写出s与t的函数关系(不需要写出自变量的取值范围)
10.医药研究所试验某种新药效时,成人如果按剂量服用,血液中每毫升含药量y(毫克)随时间x的变化如图所示,如果每毫升血液中含药量超过4微克(含4微克)时治疗疾病为有效,那么有效时间是多少小时?
答案解析
1.【答案】 D
【解析】解:通过乙的图象可以看出B、C两港之间距离是90海里,故①错误,
甲从A港出发,经过B港,到达C港,乙从B港出发,到达C港,甲比乙快,所以甲、乙只会相遇一次,故②正确,
甲的速度: 30÷0.5=60 (海里/小时),
乙的速度: 90÷3=30 (海里/小时),
甲比乙快30海里/小时,故③正确,
A港距离C港 30+90=120 (海里),
120÷60=2 (小时),即甲到C港需要2小时,乙需要3小时,故④正确,
30÷(60?30)=1 (小时),即甲追上乙需要1个小时,
1个小时乙行驶了30海里,
∴ P(1,30) ,故⑤正确,
正确的有:②③④⑤.
故答案为:D.
2.【答案】 C
【解析】解:由图象可得:行驶3小时后,两车相距120千米,
∴甲车从A到B的速度= 120+3×603 =100(千米/小时),
∴AB两点距离=3×100=300(千米),
一小时后,两车相距120?60×1=60(千米),
∴甲车返回的速度= 60?60×0.40.4 =90(千米/小时),
故答案为:C.
3.【答案】 C
【解析】解:由题意得: ?=20?5t ,
∵0≤?≤20 ,
∴0≤20?5t≤20 ,
解得 0≤t≤4 ,
即h与t的关系式为 ?=20?5t(0≤t≤4) ,是一次函数图象的一部分,且h随t的增大而减小,
观察四个选项可知,只有选项C符合,
故答案为:C.
4.【答案】 C
【解析】A.由图形可知:当t=7时,乙到达B城,t=8时,甲到达B城,对应纵坐标为:780,所以两城相距780km,
故:A不符合题意;
B.因为乙车在t=1时出发,t=7时到达B城,
故:B不符合题意;
C.由图可知:甲车的速度为:480÷8=60km/h,所以t=7时,甲走的路程为:60×7=420km,此时乙所走的路程为480km,
即:480-420=60km,当乙车到达B城时,甲车距离B城60千米,故:C符合题意;
D.设甲车离开A城的距离y与行驶时间之间的函数关系为: y甲=k1t ,将(8,480)代入可求得k=60,
∴ y甲=60t ;
设乙车离开A城的距离y与行驶时间之间的函数关系为: y乙=k2t+b ,将(1,0)和(7,480)代入 y乙=k2t+b 得: {k2+b=07k2+b=480 ,
解得: {k2=80b=?80
∴ y乙=80t?80 ,
令 y甲=y乙 得:60t=80t-80,解得:t=4,
即甲车出发后4小时,乙车追上甲车,故:D不符合题意.
5.【答案】 B
【解析】A.y随x的增加而增加,x是自变量,y是因变量,故A选项不符合题意;
B. 弹簧不挂重物时的长度为10cm , 故B选项符合题意;
C. 物体质量每增加1kg , 弹簧长度y增加0.5cm , 故C选项不符合题意;
D. 由C知,y=10+0.5x , 则当x=7时,y=13.5,即所挂物体质量为7kg时,弹簧长度为13.5cm , 故D选项不符合题意;
故答案为:B.
6.【答案】 C
【解析】解:由图可知,
他们进行的是800m比赛,故①正确;
乙全程的平均速度为:800÷125=6.4m/s,故②正确;
甲摔倒之前,由图象可知甲的速度快,故③错误;
甲再次投入比赛后的平均速度为:(800?200)÷(120?40)=600÷80=7.5m/s,故④正确;
设甲乙第二次相遇的时间为ts,
6.4t=200+(t?40)×7.5,得t= 100011 ,
则甲再次投入比赛后在距离终点800?6.4× 100011 = 240011 米时追上了乙,故⑤错误.
故答案为:C.
7.【答案】 630
【解析】解:设甲车,乙车的速度分别为x千米/时,y千米/时,
甲车与乙车相向而行5小时相遇,则5(x+y)=900,解得x+y=180,
相遇后当甲车到达B地时两车相距720千米,所需时间为720÷180=4小时,
则甲车从A地到B需要9小时,故甲车的速度为900÷9=100千米/时,乙车的速度为180-100=80千米/时,
乙车行驶900-720=180千米所需时间为180÷80=2.25小时,
甲车从B地到A地的速度为900÷(16.5-5-4)=120千米/时.
所以甲车从B地向A地行驶了120×2.25=270千米,
当乙车到达A地时,甲车离A地的距离为900-270=630千米.
8.【答案】 356
【解析】解:∵声音在空气中的传播速度 v(ms) 是温度 t(℃) 的一次函数,
设 v=kt+b ,由题意得 t=0 时, v=331 ; t=5 时, v=336 ,
∴ {b=3315k+b=336 ,解得 {b=331k=1 ,
∴声音在空气中的传播速度 v(ms) 与温度 t(℃) 的函数关系式为: v=t+331 ,
当 t=25℃ 时, v=25+331=356 ,
∴当 t=25℃ 时,声音的传播速度为356 ms .
故答案为:356.
9.【答案】 解: ∵96m=9600cm ∴x=960075=128
∵122 步/分= 6130 步/秒∴y=128÷6130=384061
由题意可得 s=6130t
答: x=128 , y=384061 ,s与t的函数关系为 s=6130t .
10.【答案】 解:当 x≤2 时,设 y=kx ,
把 (2,?6) 代入上式,得 k=3 ,
∴ x≤2 时, y=3x ;
当 x≥2 时,设 y=k1x+b ,
把 (2,?6) , (10,?3) 代入上式,得 k1=?38 , b=274 ,
∴ y=?38x+274 ,
把y=4代入 y=3x ,得 x1=43 ,
把y=4代入 y=?38x+274 ,得 x2=223 ,
则 x2?x1=6 小时.
∴这个有效时间为 6 小时,
20.3一次函数的应用
学习目标
1.能用函数的观点认识一次函数、一次方程(组)与一元一次不等式之间的联系,能直观地用图形(在平面直角坐标系中)来表示方程(或方程组)的解及不等式的解,建立数形结合的思想及转化的思想.
2.能运用一次函数的性质解决简单的不等式问题及实际问题.
要点梳理
要点1
一元一次方程与一次函数
对于一次函数false,由它的函数值false就得到关于false的一元一次方程false,解这个方程得false,于是可以知道一次函数false的图像与false轴的交点坐标为false.
若已知一次函数false的图像与false轴的交点坐标,也可以知道这个交点的横坐标false,其就是一元一次方程false的根.
要点2一元一次不等式与一次函数
由一次函数false的函数值false大于0(或小于0),就得到关于false的一元一次不等式false(或false)的解集.
在一次函数false的图像上且位于false轴上方(或下方)的所有点,它们的横坐标的取值范围就是不等式false(或false)的解集.
典型例题
例1.如图所示直线反映了某公司产品的销售成本和销售收入与销售量之间的关系,则下列说法错误的是( )
A.?直线l1反映了该公司产品的销售收入与销售量之间的关系
B.?未开始销售时,该公司为销售所花的成本为2000元
C.?当销售量大于 4吨时,该公司赢利
D.?每销售1吨产品,销售收入为 500 元
【解析】解:观察图象可知直线l1反映了该公司产品的销售收入与销售量之间的关系,故A的说法正确,不符合题意;
直线l2反映了该公司产品的销售成本与销售量之间的关系,未开始销售时,该公司为销售所花的成本为2000元,故B的说法正确,不符合题意;
当销售量大于4吨时,销售收入大于销售成本,该公司赢利,故C说法正确,不符合题意;
每销售1吨产品,销售收入为1000元,故D说法错误,符合题意.
故答案为:D.
例2.某品牌热水壶的成本为50元,销售商对其销量与定价的关系进行了调查,结果如下:
定价/元
70
80
90
100
110
120
销量/把
80
100
110
100
80
60
现销售了 105 把水壶,则定价约为(?? )
A.?115 元?????????????????????????????????B.?105 元?????????????????????????????????C.?95 元?????????????????????????????????D.?85 元
【解析】解:由热水壶的销量与定价的关系可知:
当定价在70到80之间时,定价每增加1元,销量增加2把;
当定价在80到90之间时,定价每增加1元,销量增加1把;
当定价在90到100之间时,定价每增加1元,销量减少1把;
当定价在100到110之间时,定价每增加1元,销量减少2把;
当定价在110到120之间时,定价每增加1元,销量减少2把;
∵100<105<110
由表格可知定价约为
80+(105-100)÷1=80+5=85.
∴定价约为85元.
故答案为:D.
基础巩固
1.港口 A,B,C 依次在同一条直线上,甲、乙两艘船同时分别从 A,B 两港出发,匀速驶向 C 港,甲、乙两船与 B 港的距离 y (海里)与行驶时间 x (小时)之间的函数关系如图所示,则下列说法正确的有(? )
① B,C 两港之间的距离为60海里
②甲、乙两船在途中只相遇了一次
③甲船平均速度比乙船平均速度快30海里/时
④甲船到达 C 港时,乙船还需要一个小时才到达 C 港
⑤点 P 的坐标为 (1,30)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
2.甲、乙两车同时从A地出发,沿同一路线各自匀速向B地行驶,甲到达B地停留1小时后按原路以另一速度匀速返回,直到与乙车相遇.乙车的速度为每小时60千米.两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示,则下列结论错误的是(??? )
A.?行驶3小时后,两车相距120千米????????????????????????B.?甲车从A到B的速度为100千米/小时
C.?甲车返回是行驶的速度为95千米/小时????????????????D.?A,B两地之间的距离为300千米
3.一根蜡烛长20cm , 点燃后每小时燃烧5cm燃烧时剩下的高度h(cm)与时间t(小时)的关系图象表示是( )
A.???????????????B.???????????????C.???????????????D.?
4.甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(单位:km)与甲车行驶时间x(单位:h)之间的函数关系如图所示,根据图象提供的信息,下列结论错误的是(????? )
A.?两城相距480千米???????????????????????????????????????????????B.?乙车比甲车晚出发1小时,却早到1小时
C.?当乙车到达B城时,甲车距离B城80千米?????????????D.?甲车出发后4小时,乙车追上甲车
5.弹簧挂上物体后会伸长,测得一弹簧的长度y (cm)与所挂的物体的质量x(kg)之间有下面的关系:
x/kg
0
1
2
3
4
5
y/cm
10
10.5
11
11.5
12
12.5
下列说法错误的是(???? )
A.?x与y都是变量,且x是自变量,y是因变量???????????B.?弹簧不挂重物时的长度为0 cm
C.?物体质量每增加1 kg,弹簧长度y增加0.5 cm??????D.?所挂物体质量为7 kg时,弹簧长度为13.5 cm
6.在运动会径赛中,甲、乙两人同时起跑,刚跑出200米甲不慎摔倒,他又迅速地爬起来继续投入比赛.他们所跑的路程 y(m) 与比赛时间 x(s) 的关系如图,有下列说法:
①他们进行的是 800m 比赛; ②乙全程的平均速度为 6.4m/s ③甲摔倒之前,乙的速度快:④甲再次投入比赛后的平均速度为 7.5m/s ;⑤甲再次投入比赛后在距离终点300米时追上了乙其中正确的个数有(?? )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
7.甲、乙两车分别从A、B两地同时出发,相向行驶,已知甲车的速度大于乙车的速度,甲车到达B地后马上以另一速度原路返回A地(掉头的时间忽略不计),乙车到达A地以后即停在地等待甲车.如图所示为甲乙两车间的距离y(千米)与甲车的行驶时间t(小时)之间的函数图象,则当乙车到达A地的时候,甲车与A地的距离为________千米.
8.声音在空气中的传播速度 v(ms) 与温度 t(℃) 的关系如表:
温度(℃)
0
5
10
15
20
速度 v(ms)
331
336
341
346
351
若声音在空气中的传播速度 v(ms) 是温度 t(℃) 的一次函数;当 t=25℃ 时,声音的传播速度为________ ms .
9.今年10月1日上午,庆祝中华人民共和国成立70周年阅兵式在天安门正式举行.通常提到的“阅兵”,实际是分为“阅兵式”和“分列式”.阅兵式,就是士兵不动,军委主席坐车来检阅.分列式,就是所有方(梯)队,踏着统一的节奏,依次通过天安门前检阅区.在分列式中,受检阅的距离就是天安门前,东西的两个华表之间,两个华表相隔 96 米.受检阅官兵迈着每步 75 厘米,必需x步走完,若步速每分钟 122 步,需要时间y秒.求出x与y各是多少?若淮北籍东海舰队航空兵副司令员梁旭少将在受检阅时,他走过的路程s步,行走的时间为t秒写出s与t的函数关系(不需要写出自变量的取值范围)
10.医药研究所试验某种新药效时,成人如果按剂量服用,血液中每毫升含药量y(毫克)随时间x的变化如图所示,如果每毫升血液中含药量超过4微克(含4微克)时治疗疾病为有效,那么有效时间是多少小时?
答案解析
1.【答案】 D
【解析】解:通过乙的图象可以看出B、C两港之间距离是90海里,故①错误,
甲从A港出发,经过B港,到达C港,乙从B港出发,到达C港,甲比乙快,所以甲、乙只会相遇一次,故②正确,
甲的速度: 30÷0.5=60 (海里/小时),
乙的速度: 90÷3=30 (海里/小时),
甲比乙快30海里/小时,故③正确,
A港距离C港 30+90=120 (海里),
120÷60=2 (小时),即甲到C港需要2小时,乙需要3小时,故④正确,
30÷(60?30)=1 (小时),即甲追上乙需要1个小时,
1个小时乙行驶了30海里,
∴ P(1,30) ,故⑤正确,
正确的有:②③④⑤.
故答案为:D.
2.【答案】 C
【解析】解:由图象可得:行驶3小时后,两车相距120千米,
∴甲车从A到B的速度= 120+3×603 =100(千米/小时),
∴AB两点距离=3×100=300(千米),
一小时后,两车相距120?60×1=60(千米),
∴甲车返回的速度= 60?60×0.40.4 =90(千米/小时),
故答案为:C.
3.【答案】 C
【解析】解:由题意得: ?=20?5t ,
∵0≤?≤20 ,
∴0≤20?5t≤20 ,
解得 0≤t≤4 ,
即h与t的关系式为 ?=20?5t(0≤t≤4) ,是一次函数图象的一部分,且h随t的增大而减小,
观察四个选项可知,只有选项C符合,
故答案为:C.
4.【答案】 C
【解析】A.由图形可知:当t=7时,乙到达B城,t=8时,甲到达B城,对应纵坐标为:780,所以两城相距780km,
故:A不符合题意;
B.因为乙车在t=1时出发,t=7时到达B城,
故:B不符合题意;
C.由图可知:甲车的速度为:480÷8=60km/h,所以t=7时,甲走的路程为:60×7=420km,此时乙所走的路程为480km,
即:480-420=60km,当乙车到达B城时,甲车距离B城60千米,故:C符合题意;
D.设甲车离开A城的距离y与行驶时间之间的函数关系为: y甲=k1t ,将(8,480)代入可求得k=60,
∴ y甲=60t ;
设乙车离开A城的距离y与行驶时间之间的函数关系为: y乙=k2t+b ,将(1,0)和(7,480)代入 y乙=k2t+b 得: {k2+b=07k2+b=480 ,
解得: {k2=80b=?80
∴ y乙=80t?80 ,
令 y甲=y乙 得:60t=80t-80,解得:t=4,
即甲车出发后4小时,乙车追上甲车,故:D不符合题意.
5.【答案】 B
【解析】A.y随x的增加而增加,x是自变量,y是因变量,故A选项不符合题意;
B. 弹簧不挂重物时的长度为10cm , 故B选项符合题意;
C. 物体质量每增加1kg , 弹簧长度y增加0.5cm , 故C选项不符合题意;
D. 由C知,y=10+0.5x , 则当x=7时,y=13.5,即所挂物体质量为7kg时,弹簧长度为13.5cm , 故D选项不符合题意;
故答案为:B.
6.【答案】 C
【解析】解:由图可知,
他们进行的是800m比赛,故①正确;
乙全程的平均速度为:800÷125=6.4m/s,故②正确;
甲摔倒之前,由图象可知甲的速度快,故③错误;
甲再次投入比赛后的平均速度为:(800?200)÷(120?40)=600÷80=7.5m/s,故④正确;
设甲乙第二次相遇的时间为ts,
6.4t=200+(t?40)×7.5,得t= 100011 ,
则甲再次投入比赛后在距离终点800?6.4× 100011 = 240011 米时追上了乙,故⑤错误.
故答案为:C.
7.【答案】 630
【解析】解:设甲车,乙车的速度分别为x千米/时,y千米/时,
甲车与乙车相向而行5小时相遇,则5(x+y)=900,解得x+y=180,
相遇后当甲车到达B地时两车相距720千米,所需时间为720÷180=4小时,
则甲车从A地到B需要9小时,故甲车的速度为900÷9=100千米/时,乙车的速度为180-100=80千米/时,
乙车行驶900-720=180千米所需时间为180÷80=2.25小时,
甲车从B地到A地的速度为900÷(16.5-5-4)=120千米/时.
所以甲车从B地向A地行驶了120×2.25=270千米,
当乙车到达A地时,甲车离A地的距离为900-270=630千米.
8.【答案】 356
【解析】解:∵声音在空气中的传播速度 v(ms) 是温度 t(℃) 的一次函数,
设 v=kt+b ,由题意得 t=0 时, v=331 ; t=5 时, v=336 ,
∴ {b=3315k+b=336 ,解得 {b=331k=1 ,
∴声音在空气中的传播速度 v(ms) 与温度 t(℃) 的函数关系式为: v=t+331 ,
当 t=25℃ 时, v=25+331=356 ,
∴当 t=25℃ 时,声音的传播速度为356 ms .
故答案为:356.
9.【答案】 解: ∵96m=9600cm ∴x=960075=128
∵122 步/分= 6130 步/秒∴y=128÷6130=384061
由题意可得 s=6130t
答: x=128 , y=384061 ,s与t的函数关系为 s=6130t .
10.【答案】 解:当 x≤2 时,设 y=kx ,
把 (2,?6) 代入上式,得 k=3 ,
∴ x≤2 时, y=3x ;
当 x≥2 时,设 y=k1x+b ,
把 (2,?6) , (10,?3) 代入上式,得 k1=?38 , b=274 ,
∴ y=?38x+274 ,
把y=4代入 y=3x ,得 x1=43 ,
把y=4代入 y=?38x+274 ,得 x2=223 ,
则 x2?x1=6 小时.
∴这个有效时间为 6 小时,
