22.3梯形 讲义-2020-2021学年沪教版(上海)八年级数学下册(机构)(word版含解析)
文档属性
| 名称 | 22.3梯形 讲义-2020-2021学年沪教版(上海)八年级数学下册(机构)(word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 100.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-01 00:00:00 | ||
图片预览




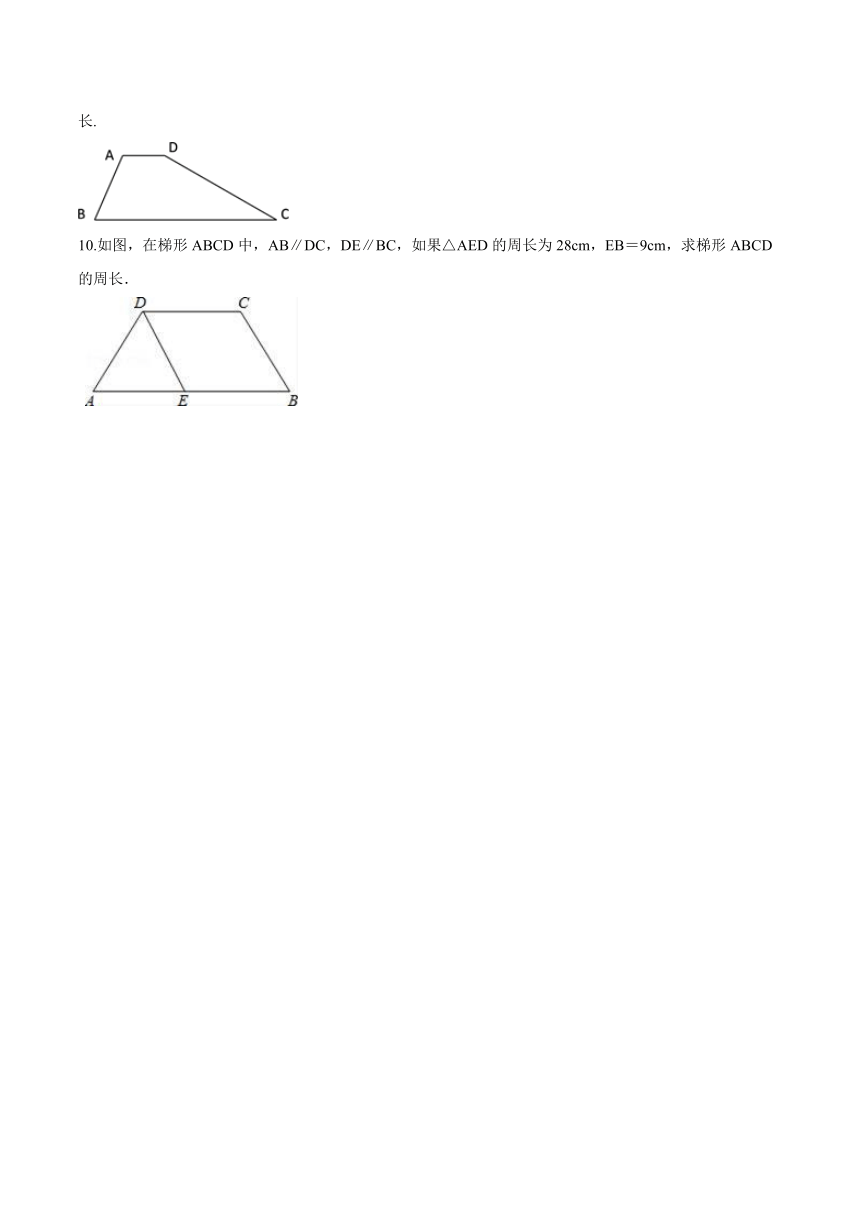
文档简介
1285875-30289522.3梯形
22.3梯形
学习目标
1.熟练掌握特殊梯形的证明;
2.灵活的运用中位线的相关性质解决边和角的相关数量问题.
要点梳理
一、梯形及梯形的有关概念
(1)梯形:一组对边平行而另一组对边不平行的四边形叫做梯形.
底:平行的两边叫做底,其中较长的是下底,较短的叫上底.
腰:不平行的两边叫做腰.
高:梯形两底之间的距离叫做高.
(2)特殊梯形
396240113030
624840333375 直角梯形:一腰垂直于底的梯形叫做直角梯形.
特殊梯形
等腰梯形:两腰相等的梯形叫做等腰梯形.
思考讨论:若上面两个条件同时成立是否是梯形?
交流:如果同时具备直角梯形和等腰梯形的特征,那么该图形是矩形.
【等腰梯形性质】
等腰梯形性质定理1等腰梯形在同一底上的两个内角相等.
等腰梯形性质定理2等腰梯形的两条对角线相等.
另外:等腰梯形是轴对称图形;
【等腰梯形判定】
等腰梯形判定定理1在同一底边上的两个内角相等的梯形是等腰梯形.
等腰梯形判定定理2对角线相等的梯形是等腰梯形.
典型例题
例1.如图,D、E分别是△ABC的边AB、AC的中点,若BC=6,则DE=(? )
A.?2???????????????????????????????????????????B.?3???????????????????????????????????????????C.?4???????????????????????????????????????????D.?5
【解析】解:∵D、E分别是△ABC的边AB、AC的中点,
∴DE是△ABC的中位线,
∴DE= 12 BC=3,
故答案为:B.
例2.下列四个命题中,假命题是(?????? )
A.?有两个内角相等的梯形是等腰梯形??????????????????????B.?等腰梯形一定有两个内角相等
C.?两条对角线相等的梯形是等腰梯形??????????????????????D.?等腰梯形的两条对角线相等
【解析】解:A、有两个内角相等的梯形是等腰梯形,如:直角梯形,故这个命题为假命题;
B、等腰梯形一定有两个内角相等,这个命题为真命题;
C、两条对角线相等的梯形是等腰梯形,这个命题为真命题;
D、等腰梯形的两条对角线相等,这个命题为真命题.
故答案为:A.
基础巩固
1.如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,如果△ABC的周长为20,那么△DEF的周长是( ??)
A.?20?????????????????????????????????????????B.?15?????????????????????????????????????????C.?10?????????????????????????????????????????D.?5
2.在梯形 ABCD 中, AD // BC ,那么下列条件中,不能判断它是等腰梯形的是(???? )
A.?AB=DC????????????????B.?∠DAB=∠ABC????????????????C.?∠ABC=∠DCB????????????????D.?AC=DB
3.在课外活动课上,教师让同学们作一个对角线完全垂直的等腰梯形形状的风筝,其面积为800平方厘米,则对角线所用的竹条至少需(?? )
A.?40 2 cm?????????????????????????????B.?40cm?????????????????????????????C.?80cm?????????????????????????????D.?80 2 cm
4.如图,在等腰梯形ABCD中,AD∥BC,对角线AC.BD相交于点O,下列结论不一定正确的是(? )
A.?AC=BD???????????????????????B.?OB=OC???????????????????????C.?∠BCD=∠BDC???????????????????????D.?∠ABD=∠ACD
5.如图,在梯形ABCD中,AD∥BC,EF是梯形ABCD的中位线,若△BEF的面积为4cm2 , 则梯形ABCD的面积为(?? )
A.?8cm2????????????????????????????????B.?12cm2????????????????????????????????C.?16cm2????????????????????????????????D.?20cm2
6.如图,边长为1的正方形EFGH在边长为3的正方形ABCD所在平面上移动,始终保持EF∥AB.线段CF的中点为M,DH的中点为N,则线段MN的长为(?????? )
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
7.如图,直线 l1⊥x 轴于点 (1?,??0) ,直线 l2⊥x 轴于点 (2?,??0) ,直线 l3⊥x 轴于点 (3?,??0) ,…,直线 ln⊥x 轴于点 (n?,??0) (其中 n 为正整数).函数 y=x 的图象与直线 l1 , l2 , l3 ,…, ln 分别交于点 A1 , A2 , A3 ,…, An ;函数 y=2x 的图象与直线 l1 , l2 , l3 ,…, ln 分别交于点 B1 , B2 , B3 ,…, Bn ,如果 △OA1B1 的面积记作 S1 ,四边形 A1A2B2B1 的面积记作 S2 ,四边形 A2A3B3B2 的面积记作 S3 ,…,四边形 An?1AnBnBn?1 的面积记作 Sn ,那么 S2015= ________.
8.已知点A、B到直线l的距离分别为4与6,O是线段AB的中点,那么点O到直线l的距离是________.
9.已知:如图,梯形ABCD中,AD∥BC,∠B=60°,∠C=30°,AD=4,BC=10.求:梯形两腰AB、CD的长.
10.如图,在梯形ABCD中,AB∥DC,DE∥BC,如果△AED的周长为28cm,EB=9cm,求梯形ABCD的周长.
答案解析
1.【答案】 C
【解析】∵D、E分别是△ABC的边BC、AB的中点,
∴DE= 12 AC,同理 EF= 12 BC,DF= 12 AB,∴C△DEF=DE+EF+DF= 12 (AC+BC+AB)= 12 ×20=10.
故答案为:C.
2.【答案】 B
【解析】解:A、∵四边形ABCD为梯形,且 AD // BC , AB=DC ,∴四边形ABCD是等腰梯形,故本选项不符合题意;
B、∠DAB=∠ABC,不能推出四边形ABCD是等腰梯形,故本选项符合题意;
C、∵四边形ABCD为梯形,且 AD // BC ,∠ABC=∠DCB,∴四边形ABCD是等腰梯形,故本选项不符合题意;
D、∵四边形ABCD为梯形,且 AD // BC , AC=DB ,∴四边形ABCD是等腰梯形,故本选项不符合题意.
故答案为:B.
3.【答案】 B
【解析】解:∵四边形是等腰梯形
∴梯形的两条对角线相等
∵对角线相互垂直,设对角线长度为a,根据面积公式得: S=12·a·a
即:800= 12a2 ,解得:a=40
故答案为:B
4.【答案】 C
【解析】解:A.∵四边形ABCD是等腰梯形,∴AC=BD,故本选项不符合题意.
B.∵四边形ABCD是等腰梯形,∴AB=DC,∠ABC=∠DCB,
∵在△ABC和△DCB中,AB=DC,∠ABC=∠DCB,BC=CB,
∴△ABC≌△DCB(SAS).∴∠ACB=∠DBC.∴OB=OC.故本选项不符合题意.
C.∵BC和BD不一定相等,∴∠BCD与∠BDC不一定相等,故本选项符合题意.
D.∵∠ABC=∠DCB,∠ACB=∠DBC,∴∠ABD=∠ACD.故本选项不符合题意.
故答案为:C.
5.【答案】 C
【解析】解:如图,过A作AN⊥BC于N,交EF于M,
∵EF是梯形ABCD的中位线,
∴AD+BC=2EF,EF∥AD∥BC,
∴AM⊥EF,AM=MN,
∵△BEF的面积为4cm2 ,
∴ 12 EF×AM=4,
∴EF×AM=8,
∴梯形ABCD的面积为 12 (AD+BC)×AN= 12 ×2EF×2AM=2EF×AM=16cm2 ,
故答案为:C.
6.【答案】 B
【解析】解:如图,将正方形EFGH的位置特殊化,使点H与点A重合,过点M作MO⊥ED于点O,则MO是梯形CDEF的中位线,
∴EO=OD=2,MO=12(EF+CD)=2.
∵点M、N分别是FC、AD的中点,
∴AN=ND=32 ,
∴ON=OD-ND=2-32=12.
在Rt△MON中,MN2=MO2+ON2 , 即MN=22+122=172.
故答案为:B.
7.【答案】 2014.5
【解析】解:∵ ln?1 ⊥x轴, ln ⊥x轴,
∴An﹣1Bn﹣1∥AnBn , 且 ln?1 与 ln 的距离为1,
∴四边形 An?1AnBnBn?1 是梯形,An(n,n),Bn(n,2n),
根据题意,AnBn=2n﹣n=n,An﹣1Bn﹣1=n﹣1,
∴四边形 An?1AnBnBn?1 的面积 Sn = 12 (n+n﹣1)×1= 12 (2n﹣1),
∴当n=2015时, S2015 = 12 ×(2×2015﹣1)=2014.5,
故答案为:2014.5.
8.【答案】 5或1
【解析】解:如图一,作AD⊥l于D , BC⊥l于C , OF⊥l于F .
∵AD⊥l于D , BC⊥l , OF⊥l于F ,
∴AD∥OF∥BC ,
∴ABCD是直角梯形,
∵O是AB的中点,AD=4,BC=6,
∴DF=CF ,
∴OF= 12 (AD+BC)= 12 (4+6)=5.
如图二,作AD⊥l于D , BC⊥l于C , OF⊥l于F .
∵AD⊥l于D , BC⊥l , OF⊥l于F ,
∴AD∥OF∥BC ,
连接DO并延长,交BC于G , 则易得△AOD≌△BOG ,
∴BG=AD=4,DO=GO ,
又∵BC=6,
∴CG=6﹣4=2,
∵OF∥CG ,
∴DF=CF ,
∴OF= 12 CG=1,
故答案为:5或1.
9.【答案】 解:作DE∥AB交BC于点E,则四边形ABED是平行四边形.
∴AB=DE,AD=BE,∠DEC=∠B=60°,
∵∠C=30°,
∴∠EDC=180°-60°-30°=90°,
∵CE=BC-BE=BC-AD=6,
∴DE=3,CD=3 3 ,
即AB=3,CD=3 3 .
故答案为:AB=3,CD=3 3 .
10.【答案】 梯形ABCD的周长是46cm.
【解析】∵AB∥DC,DE∥CB(已知),∴四边形DEBC是平行四边形(两组对边互相平行的四边形是平行四边形);
∴CD=BE=9cm,DE=BC(平行四边形的对边相等),∴梯形ABCD的周长
=AD+AB+BC+CD=AD+AE+DE+BE+CD=△ADE的周长+BE+CD=28cm+9cm+9cm=46cm,即梯形ABCD的周长是46cm.
22.3梯形
学习目标
1.熟练掌握特殊梯形的证明;
2.灵活的运用中位线的相关性质解决边和角的相关数量问题.
要点梳理
一、梯形及梯形的有关概念
(1)梯形:一组对边平行而另一组对边不平行的四边形叫做梯形.
底:平行的两边叫做底,其中较长的是下底,较短的叫上底.
腰:不平行的两边叫做腰.
高:梯形两底之间的距离叫做高.
(2)特殊梯形
396240113030
624840333375 直角梯形:一腰垂直于底的梯形叫做直角梯形.
特殊梯形
等腰梯形:两腰相等的梯形叫做等腰梯形.
思考讨论:若上面两个条件同时成立是否是梯形?
交流:如果同时具备直角梯形和等腰梯形的特征,那么该图形是矩形.
【等腰梯形性质】
等腰梯形性质定理1等腰梯形在同一底上的两个内角相等.
等腰梯形性质定理2等腰梯形的两条对角线相等.
另外:等腰梯形是轴对称图形;
【等腰梯形判定】
等腰梯形判定定理1在同一底边上的两个内角相等的梯形是等腰梯形.
等腰梯形判定定理2对角线相等的梯形是等腰梯形.
典型例题
例1.如图,D、E分别是△ABC的边AB、AC的中点,若BC=6,则DE=(? )
A.?2???????????????????????????????????????????B.?3???????????????????????????????????????????C.?4???????????????????????????????????????????D.?5
【解析】解:∵D、E分别是△ABC的边AB、AC的中点,
∴DE是△ABC的中位线,
∴DE= 12 BC=3,
故答案为:B.
例2.下列四个命题中,假命题是(?????? )
A.?有两个内角相等的梯形是等腰梯形??????????????????????B.?等腰梯形一定有两个内角相等
C.?两条对角线相等的梯形是等腰梯形??????????????????????D.?等腰梯形的两条对角线相等
【解析】解:A、有两个内角相等的梯形是等腰梯形,如:直角梯形,故这个命题为假命题;
B、等腰梯形一定有两个内角相等,这个命题为真命题;
C、两条对角线相等的梯形是等腰梯形,这个命题为真命题;
D、等腰梯形的两条对角线相等,这个命题为真命题.
故答案为:A.
基础巩固
1.如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,如果△ABC的周长为20,那么△DEF的周长是( ??)
A.?20?????????????????????????????????????????B.?15?????????????????????????????????????????C.?10?????????????????????????????????????????D.?5
2.在梯形 ABCD 中, AD // BC ,那么下列条件中,不能判断它是等腰梯形的是(???? )
A.?AB=DC????????????????B.?∠DAB=∠ABC????????????????C.?∠ABC=∠DCB????????????????D.?AC=DB
3.在课外活动课上,教师让同学们作一个对角线完全垂直的等腰梯形形状的风筝,其面积为800平方厘米,则对角线所用的竹条至少需(?? )
A.?40 2 cm?????????????????????????????B.?40cm?????????????????????????????C.?80cm?????????????????????????????D.?80 2 cm
4.如图,在等腰梯形ABCD中,AD∥BC,对角线AC.BD相交于点O,下列结论不一定正确的是(? )
A.?AC=BD???????????????????????B.?OB=OC???????????????????????C.?∠BCD=∠BDC???????????????????????D.?∠ABD=∠ACD
5.如图,在梯形ABCD中,AD∥BC,EF是梯形ABCD的中位线,若△BEF的面积为4cm2 , 则梯形ABCD的面积为(?? )
A.?8cm2????????????????????????????????B.?12cm2????????????????????????????????C.?16cm2????????????????????????????????D.?20cm2
6.如图,边长为1的正方形EFGH在边长为3的正方形ABCD所在平面上移动,始终保持EF∥AB.线段CF的中点为M,DH的中点为N,则线段MN的长为(?????? )
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
7.如图,直线 l1⊥x 轴于点 (1?,??0) ,直线 l2⊥x 轴于点 (2?,??0) ,直线 l3⊥x 轴于点 (3?,??0) ,…,直线 ln⊥x 轴于点 (n?,??0) (其中 n 为正整数).函数 y=x 的图象与直线 l1 , l2 , l3 ,…, ln 分别交于点 A1 , A2 , A3 ,…, An ;函数 y=2x 的图象与直线 l1 , l2 , l3 ,…, ln 分别交于点 B1 , B2 , B3 ,…, Bn ,如果 △OA1B1 的面积记作 S1 ,四边形 A1A2B2B1 的面积记作 S2 ,四边形 A2A3B3B2 的面积记作 S3 ,…,四边形 An?1AnBnBn?1 的面积记作 Sn ,那么 S2015= ________.
8.已知点A、B到直线l的距离分别为4与6,O是线段AB的中点,那么点O到直线l的距离是________.
9.已知:如图,梯形ABCD中,AD∥BC,∠B=60°,∠C=30°,AD=4,BC=10.求:梯形两腰AB、CD的长.
10.如图,在梯形ABCD中,AB∥DC,DE∥BC,如果△AED的周长为28cm,EB=9cm,求梯形ABCD的周长.
答案解析
1.【答案】 C
【解析】∵D、E分别是△ABC的边BC、AB的中点,
∴DE= 12 AC,同理 EF= 12 BC,DF= 12 AB,∴C△DEF=DE+EF+DF= 12 (AC+BC+AB)= 12 ×20=10.
故答案为:C.
2.【答案】 B
【解析】解:A、∵四边形ABCD为梯形,且 AD // BC , AB=DC ,∴四边形ABCD是等腰梯形,故本选项不符合题意;
B、∠DAB=∠ABC,不能推出四边形ABCD是等腰梯形,故本选项符合题意;
C、∵四边形ABCD为梯形,且 AD // BC ,∠ABC=∠DCB,∴四边形ABCD是等腰梯形,故本选项不符合题意;
D、∵四边形ABCD为梯形,且 AD // BC , AC=DB ,∴四边形ABCD是等腰梯形,故本选项不符合题意.
故答案为:B.
3.【答案】 B
【解析】解:∵四边形是等腰梯形
∴梯形的两条对角线相等
∵对角线相互垂直,设对角线长度为a,根据面积公式得: S=12·a·a
即:800= 12a2 ,解得:a=40
故答案为:B
4.【答案】 C
【解析】解:A.∵四边形ABCD是等腰梯形,∴AC=BD,故本选项不符合题意.
B.∵四边形ABCD是等腰梯形,∴AB=DC,∠ABC=∠DCB,
∵在△ABC和△DCB中,AB=DC,∠ABC=∠DCB,BC=CB,
∴△ABC≌△DCB(SAS).∴∠ACB=∠DBC.∴OB=OC.故本选项不符合题意.
C.∵BC和BD不一定相等,∴∠BCD与∠BDC不一定相等,故本选项符合题意.
D.∵∠ABC=∠DCB,∠ACB=∠DBC,∴∠ABD=∠ACD.故本选项不符合题意.
故答案为:C.
5.【答案】 C
【解析】解:如图,过A作AN⊥BC于N,交EF于M,
∵EF是梯形ABCD的中位线,
∴AD+BC=2EF,EF∥AD∥BC,
∴AM⊥EF,AM=MN,
∵△BEF的面积为4cm2 ,
∴ 12 EF×AM=4,
∴EF×AM=8,
∴梯形ABCD的面积为 12 (AD+BC)×AN= 12 ×2EF×2AM=2EF×AM=16cm2 ,
故答案为:C.
6.【答案】 B
【解析】解:如图,将正方形EFGH的位置特殊化,使点H与点A重合,过点M作MO⊥ED于点O,则MO是梯形CDEF的中位线,
∴EO=OD=2,MO=12(EF+CD)=2.
∵点M、N分别是FC、AD的中点,
∴AN=ND=32 ,
∴ON=OD-ND=2-32=12.
在Rt△MON中,MN2=MO2+ON2 , 即MN=22+122=172.
故答案为:B.
7.【答案】 2014.5
【解析】解:∵ ln?1 ⊥x轴, ln ⊥x轴,
∴An﹣1Bn﹣1∥AnBn , 且 ln?1 与 ln 的距离为1,
∴四边形 An?1AnBnBn?1 是梯形,An(n,n),Bn(n,2n),
根据题意,AnBn=2n﹣n=n,An﹣1Bn﹣1=n﹣1,
∴四边形 An?1AnBnBn?1 的面积 Sn = 12 (n+n﹣1)×1= 12 (2n﹣1),
∴当n=2015时, S2015 = 12 ×(2×2015﹣1)=2014.5,
故答案为:2014.5.
8.【答案】 5或1
【解析】解:如图一,作AD⊥l于D , BC⊥l于C , OF⊥l于F .
∵AD⊥l于D , BC⊥l , OF⊥l于F ,
∴AD∥OF∥BC ,
∴ABCD是直角梯形,
∵O是AB的中点,AD=4,BC=6,
∴DF=CF ,
∴OF= 12 (AD+BC)= 12 (4+6)=5.
如图二,作AD⊥l于D , BC⊥l于C , OF⊥l于F .
∵AD⊥l于D , BC⊥l , OF⊥l于F ,
∴AD∥OF∥BC ,
连接DO并延长,交BC于G , 则易得△AOD≌△BOG ,
∴BG=AD=4,DO=GO ,
又∵BC=6,
∴CG=6﹣4=2,
∵OF∥CG ,
∴DF=CF ,
∴OF= 12 CG=1,
故答案为:5或1.
9.【答案】 解:作DE∥AB交BC于点E,则四边形ABED是平行四边形.
∴AB=DE,AD=BE,∠DEC=∠B=60°,
∵∠C=30°,
∴∠EDC=180°-60°-30°=90°,
∵CE=BC-BE=BC-AD=6,
∴DE=3,CD=3 3 ,
即AB=3,CD=3 3 .
故答案为:AB=3,CD=3 3 .
10.【答案】 梯形ABCD的周长是46cm.
【解析】∵AB∥DC,DE∥CB(已知),∴四边形DEBC是平行四边形(两组对边互相平行的四边形是平行四边形);
∴CD=BE=9cm,DE=BC(平行四边形的对边相等),∴梯形ABCD的周长
=AD+AB+BC+CD=AD+AE+DE+BE+CD=△ADE的周长+BE+CD=28cm+9cm+9cm=46cm,即梯形ABCD的周长是46cm.
