22.2平行四边形 讲义-2020-2021学年沪教版(上海)八年级数学下册(机构)(含答案)
文档属性
| 名称 | 22.2平行四边形 讲义-2020-2021学年沪教版(上海)八年级数学下册(机构)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 112.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 00:00:00 | ||
图片预览


文档简介
1285875-30289522.2平行四边形
22.2平行四边形
学习目标
1.理解平行四边形的概念,掌握平行四边形的性质定理,并会应用平行四边形的性质定理和判定定理解决简单的几何证明和几何计算问题.
要点梳理
两组对边分别平行的四边形叫做平行四边形.平行四边形用符号“false”表示,
如:falseABCD.
2、平行四边形性质定理
①如果一个四边形是平行四边形,那么这个四边形的两组对边分别相等.
简述为:平行四边形的对边相等.
②如果一个四边形是平行四边形,那么这个四边形的两组对角分别相等.
简述为:平行四边形的对角相等.
③如果一个四边形是平行四边形,那么这个四边形的两条对角线互相平分.
简述为:平行四边形的两条对角线互相平分.
④平行四边形是中心对称图形,对称中心是两条对角线的交点.
⑤推论:夹在两条平行线间的平行线段相等.
典型例题
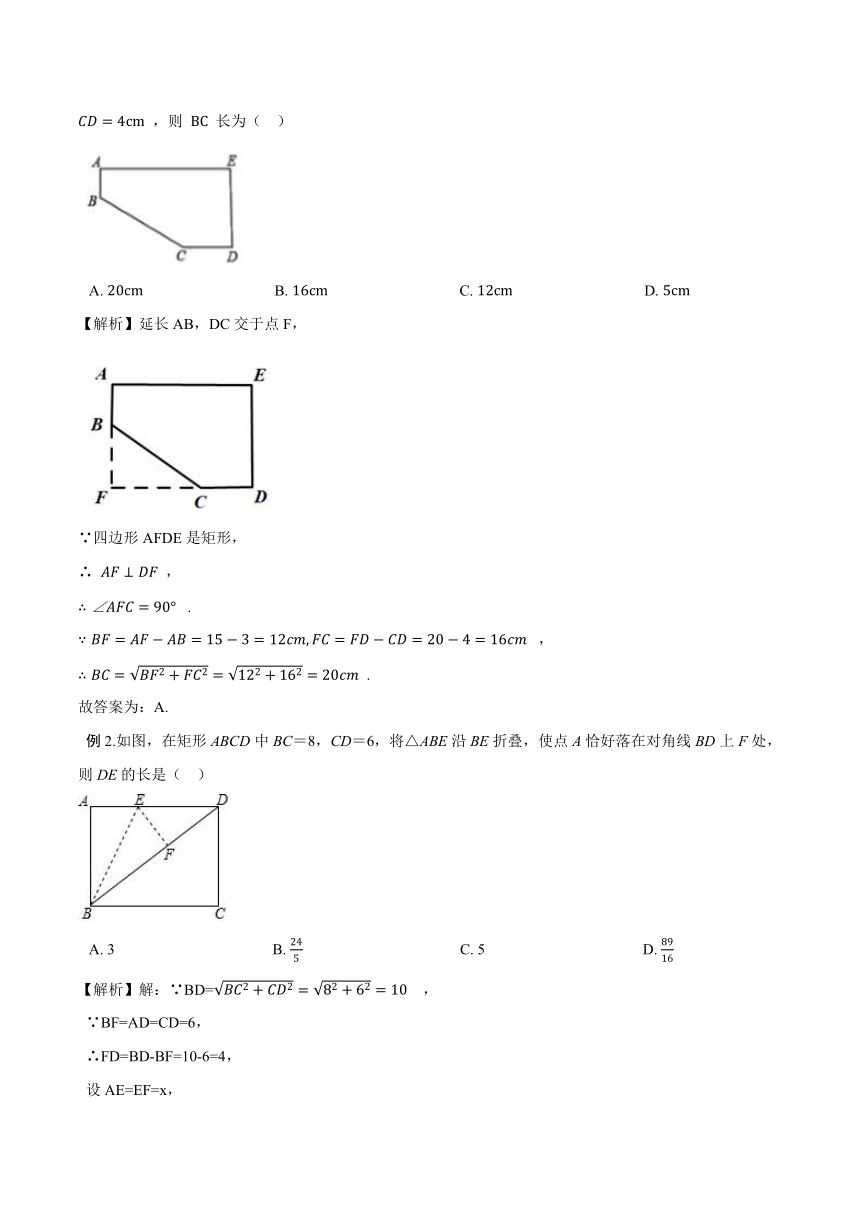
例1.如图,小明将一张长为 20cm ,宽为 15cm 的长方形纸 (AE>DE) 剪去了一角,量得 AB=3cm , CD=4cm ,则 BC 长为(?? )
A.?20cm??????????????????????????????????B.?16cm??????????????????????????????????C.?12cm??????????????????????????????????D.?5cm
【解析】延长AB,DC交于点F,
∵四边形AFDE是矩形,
∴ AF⊥DF ,
∴∠AFC=90° ?.
∵BF=AF?AB=15?3=12cm,FC=FD?CD=20?4=16cm ?,
∴BC=BF2+FC2=122+162=20cm .
故答案为:A.
例2.如图,在矩形ABCD中BC=8,CD=6,将△ABE沿BE折叠,使点A恰好落在对角线BD上F处,则DE的长是(?? )
A.?3?????????????????????????????????????????B.?245?????????????????????????????????????????C.?5?????????????????????????????????????????D.?8916
【解析】解:∵BD=BC2+CD2=82+62=10 ,
∵BF=AD=CD=6,
∴FD=BD-BF=10-6=4,
设AE=EF=x,
∴DE=AD-AE=8-x,
∵EF2+FD2=ED2 ,
∴x2+42=(8-x)2 ,
解得x=3,
∴DE=AD-AE=8-3=5,
故答案为:C.
基础巩固
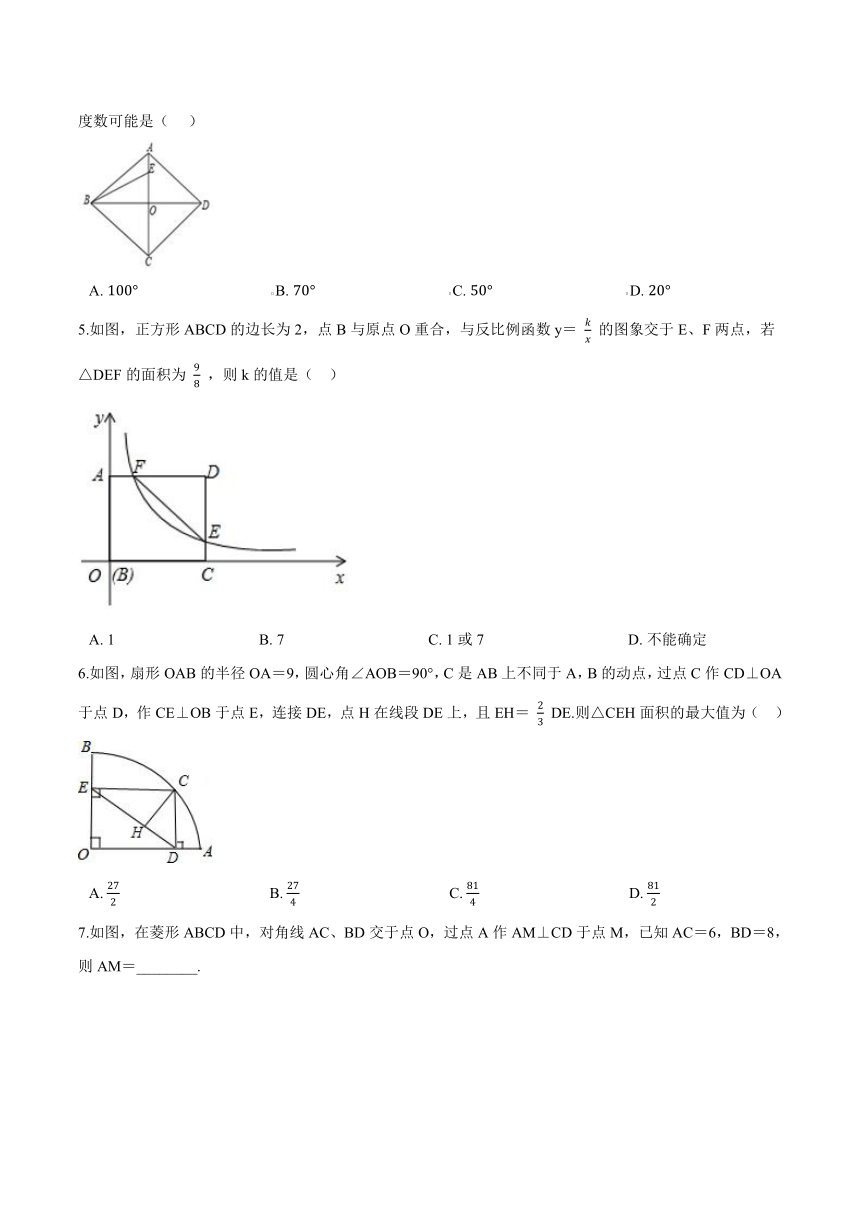
1.如图,矩形 ABCD 中, AB=2 ,点 E 在边 AD 上, EB 平分 ∠AEC , ∠DCE=45° ,则 AE 长(?? )
A.?2????????????????????????????????????B.?22?2????????????????????????????????????C.?2?2????????????????????????????????????D.?2
2.如图,菱形ABCD的面积为24,对角线AG与BD交于点O,E是BC边的中点, EF⊥BD 于点F, EG⊥AC 于点G,则四边形EFOG的面积为(?? )
A.?3???????????????????????????????????????????B.?5???????????????????????????????????????????C.?6???????????????????????????????????????????D.?8
3.如图所示,在平行四边形ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则EC等于(???? )
A.?2 cm???????????????????????????????????B.?3 cm???????????????????????????????????C.?4 cm???????????????????????????????????D.?5 cm
4.如图,在菱形 ABCD 中, AC、BD 相交于 O , ∠ABC=70° , E 是线段 AO 上一点,则 ∠BEC 的度数可能是(??? )
A.?100°???????????????????????????????????B.?70°???????????????????????????????????C.?50°???????????????????????????????????D.?20°
5.如图,正方形ABCD的边长为2,点B与原点O重合,与反比例函数y= kx 的图象交于E、F两点,若△DEF的面积为 98 ,则k的值是(?? )
A.?1??????????????????????????????????????B.?7??????????????????????????????????????C.?1或7??????????????????????????????????????D.?不能确定
6.如图,扇形OAB的半径OA=9,圆心角∠AOB=90°,C是AB上不同于A,B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连接DE,点H在线段DE上,且EH= 23 DE.则△CEH面积的最大值为(?? )
A.?272???????????????????????????????????????B.?274???????????????????????????????????????C.?814???????????????????????????????????????D.?812
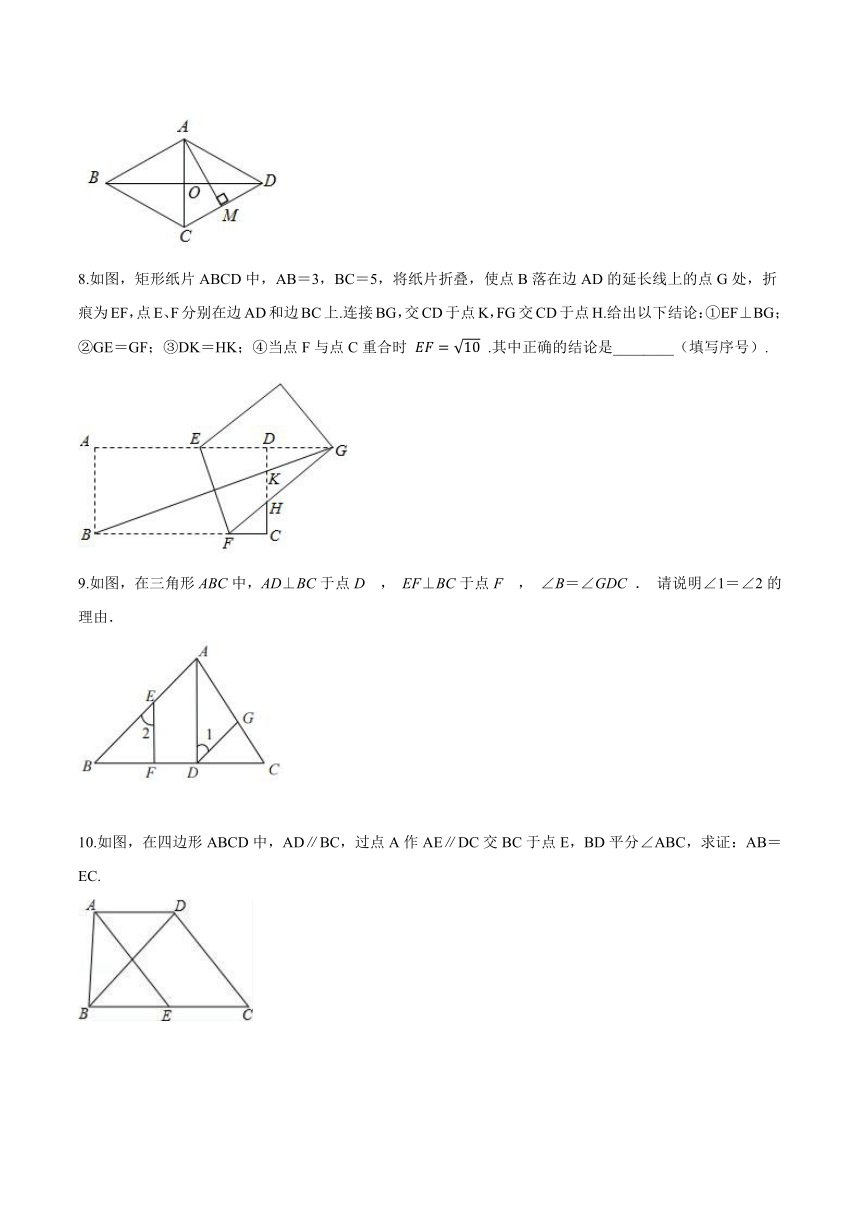
7.如图,在菱形ABCD中,对角线AC、BD交于点O,过点A作AM⊥CD于点M,已知AC=6,BD=8,则AM=________.
8.如图,矩形纸片ABCD中,AB=3,BC=5,将纸片折叠,使点B落在边AD的延长线上的点G处,折痕为EF,点E、F分别在边AD和边BC上.连接BG,交CD于点K,FG交CD于点H.给出以下结论:①EF⊥BG;②GE=GF;③DK=HK;④当点F与点C重合时 EF=10 .其中正确的结论是________(填写序号).
9.如图,在三角形ABC中,AD⊥BC于点D , EF⊥BC于点F , ∠B=∠GDC . 请说明∠1=∠2的理由.
?
10.如图,在四边形ABCD中,AD∥BC,过点A作AE∥DC交BC于点E,BD平分∠ABC,求证:AB=EC.
答案解析
1.【答案】 B
【解析】解:∵四边形ABCD是矩形, ∴AB=CD=2,∠A=∠D=∠DCB=90°,
∵∠DCE=45°,∴DE=DC=2,∴EC=2 2 ,
∵∠DCE=45°,∴∠DEC=45°,∵EB平分∠AEC,
∴∠AEB=∠BEC= 12 ∠AEC= 180°?45°2 =67.5°,∵AD∥BC∴∠AEB=∠EBC,
∴∠BEC=∠EBC,∴BC=CE=2 2 ,∴AD=BC=2 2 ,∴AE=AD-DE=2 2 -2,
故答案为:B.
2.【答案】 A
【解析】解: ∵ 四边形 ABCD 是菱形,
∴OA=OC=12AC , OB=OD=12BD , AC⊥BD ,
∵EF⊥BD 于 F , EG⊥AC 于 G ,
∴ 四边形 EFOG 是矩形, EF//OC , EG//OB ,
∵ 点 E 是线段 BC 的中点,
∴EF 、 EG 都是 △OBC 的中位线,
∴EF=12OC=14AC , EG=12OB=14BD ,
∴ 矩形 EFOG 的面积 =EF×EG=116AC·BD ;
又∵菱形ABCD的面积为= 12AC·BD=24 ,
∴ AC·BD=48
∴矩形 EFOG 的面积= 18×24=3 .
故答案为:A.
3.【答案】 A
【解析】∵在□ABCD中,AE平分∠BAD,
∴∠DAE=∠BAE,∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∵AD=5cm,AB=3cm,
∴BE=3cm,BC=5cm,
∴EC=5-3=2cm,
故答案为:A.
4.【答案】 B
【解析】∵在菱形 ABCD 中,
∴ AC⊥BD ,即:∠AOB=90°,
∴ ∠BEC <90°,
∵ ∠ABC=70° ,
∴∠ABO= 12∠ABC=12×70°=35° ,
∴∠BAO=55°,
∵ ∠BEC =∠BAO+∠ABE,
∴ ∠BEC >55°,
即:55°< ∠BEC <90°.
故答案为:B.
5.【答案】 A
【解析】解:设AF=a(a<2),则F(a,2),E(2,a),
∴FD=DE=2-a,
∴S △DEF =12DF×DE=12(2-a)2=98 ,
解得a=12或72(舍去),
∴k=2a=1,
故答案为:A.
6.【答案】 A
【解析】解:连接OC,
∵∠AOB=90°,CD⊥OA,CE⊥OB,
∴四边形ODCE是矩形,
∴DE=OC=9,
∴ CD=DE2?CE2=9?x2 ,
∵ EH=23DE ,
∴△CEH的面积为 y=23×12×EC×DC=13x×9?x2=13?(x2?812)2+(812)2
当 x2=812 时,△CEH的面积 y 有最大值,最大值为: 13×812=272
故答案为:A.
7.【答案】 245
【解析】解:∵四边形是ABCD菱形,
∴AC⊥BD, OD=12BD=4 , OC=12AC=3 , S菱形ABCD=12AC·BD=12×6×8=24 ,
∴△DOC是直角三角形,
∴ CD=OD2+OC2=5 ,
∵AM⊥CD,
∴ S菱形ABCD=AM·CD ,
∴ AM=245 .
故答案为: 245
8.【答案】 ①②④
【解析】解:连接BE,由折叠可知BO=GO,
∵EG//BF,
∴∠EGO=∠FBO,
在△EOG和△FOB中,
{∠EGO=∠FBO∠EOG=∠FOBBO=GO ,
∴△EOG≌△FOB(AAS) ,
∴EG=BF,
∴四边形EBFG是平行四边形,
由折叠可知BE=EG,
则四边形EBFG为菱形,
故EF⊥BG,GE=GF,
∴①②正确;
∵四边形EBFG为菱形,
过K作kM⊥FG于M,???????????????????????
∴KG平分∠DGH,KD⊥EG,
∴KD=KM,
在Rt△KMH中,KH为斜边,
∴KH > KM=KD,
∴③错误;
当点F与点C重合时,BE=BF=BC=5,AB=3,
在Rt△ABE中,由勾股定理AE= BE2?AB2=52?32=4 ,
∴ED=AD-AE=5-4=1,
在Rt△EDC中,由勾股定理EF= CD2+ED2=32+12=10 ,
∴④正确.
综合,正确的为①②④.
故答案为:①②④.
9.【答案】 证明:∵∠B=∠GDC,
∴DG∥AB,
∴∠1=∠BAD,
∵AD⊥BC,EF⊥BC,
∴AD∥EF,
∴∠2=∠BAD,
∴∠1=∠2.
10.【答案】 证明:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵AD∥BC,
∴∠ADB=∠CBD,
∴∠ABD=∠ADB,
∴AB=AD,
∵AD∥CE AE∥CD,
∴四边形AECD是平行四边形,
∴AD=CE,
∵AD=AB.
∴AB=CE.
22.2平行四边形
学习目标
1.理解平行四边形的概念,掌握平行四边形的性质定理,并会应用平行四边形的性质定理和判定定理解决简单的几何证明和几何计算问题.
要点梳理
两组对边分别平行的四边形叫做平行四边形.平行四边形用符号“false”表示,
如:falseABCD.
2、平行四边形性质定理
①如果一个四边形是平行四边形,那么这个四边形的两组对边分别相等.
简述为:平行四边形的对边相等.
②如果一个四边形是平行四边形,那么这个四边形的两组对角分别相等.
简述为:平行四边形的对角相等.
③如果一个四边形是平行四边形,那么这个四边形的两条对角线互相平分.
简述为:平行四边形的两条对角线互相平分.
④平行四边形是中心对称图形,对称中心是两条对角线的交点.
⑤推论:夹在两条平行线间的平行线段相等.
典型例题
例1.如图,小明将一张长为 20cm ,宽为 15cm 的长方形纸 (AE>DE) 剪去了一角,量得 AB=3cm , CD=4cm ,则 BC 长为(?? )
A.?20cm??????????????????????????????????B.?16cm??????????????????????????????????C.?12cm??????????????????????????????????D.?5cm
【解析】延长AB,DC交于点F,
∵四边形AFDE是矩形,
∴ AF⊥DF ,
∴∠AFC=90° ?.
∵BF=AF?AB=15?3=12cm,FC=FD?CD=20?4=16cm ?,
∴BC=BF2+FC2=122+162=20cm .
故答案为:A.
例2.如图,在矩形ABCD中BC=8,CD=6,将△ABE沿BE折叠,使点A恰好落在对角线BD上F处,则DE的长是(?? )
A.?3?????????????????????????????????????????B.?245?????????????????????????????????????????C.?5?????????????????????????????????????????D.?8916
【解析】解:∵BD=BC2+CD2=82+62=10 ,
∵BF=AD=CD=6,
∴FD=BD-BF=10-6=4,
设AE=EF=x,
∴DE=AD-AE=8-x,
∵EF2+FD2=ED2 ,
∴x2+42=(8-x)2 ,
解得x=3,
∴DE=AD-AE=8-3=5,
故答案为:C.
基础巩固
1.如图,矩形 ABCD 中, AB=2 ,点 E 在边 AD 上, EB 平分 ∠AEC , ∠DCE=45° ,则 AE 长(?? )
A.?2????????????????????????????????????B.?22?2????????????????????????????????????C.?2?2????????????????????????????????????D.?2
2.如图,菱形ABCD的面积为24,对角线AG与BD交于点O,E是BC边的中点, EF⊥BD 于点F, EG⊥AC 于点G,则四边形EFOG的面积为(?? )
A.?3???????????????????????????????????????????B.?5???????????????????????????????????????????C.?6???????????????????????????????????????????D.?8
3.如图所示,在平行四边形ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则EC等于(???? )
A.?2 cm???????????????????????????????????B.?3 cm???????????????????????????????????C.?4 cm???????????????????????????????????D.?5 cm
4.如图,在菱形 ABCD 中, AC、BD 相交于 O , ∠ABC=70° , E 是线段 AO 上一点,则 ∠BEC 的度数可能是(??? )
A.?100°???????????????????????????????????B.?70°???????????????????????????????????C.?50°???????????????????????????????????D.?20°
5.如图,正方形ABCD的边长为2,点B与原点O重合,与反比例函数y= kx 的图象交于E、F两点,若△DEF的面积为 98 ,则k的值是(?? )
A.?1??????????????????????????????????????B.?7??????????????????????????????????????C.?1或7??????????????????????????????????????D.?不能确定
6.如图,扇形OAB的半径OA=9,圆心角∠AOB=90°,C是AB上不同于A,B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连接DE,点H在线段DE上,且EH= 23 DE.则△CEH面积的最大值为(?? )
A.?272???????????????????????????????????????B.?274???????????????????????????????????????C.?814???????????????????????????????????????D.?812
7.如图,在菱形ABCD中,对角线AC、BD交于点O,过点A作AM⊥CD于点M,已知AC=6,BD=8,则AM=________.
8.如图,矩形纸片ABCD中,AB=3,BC=5,将纸片折叠,使点B落在边AD的延长线上的点G处,折痕为EF,点E、F分别在边AD和边BC上.连接BG,交CD于点K,FG交CD于点H.给出以下结论:①EF⊥BG;②GE=GF;③DK=HK;④当点F与点C重合时 EF=10 .其中正确的结论是________(填写序号).
9.如图,在三角形ABC中,AD⊥BC于点D , EF⊥BC于点F , ∠B=∠GDC . 请说明∠1=∠2的理由.
?
10.如图,在四边形ABCD中,AD∥BC,过点A作AE∥DC交BC于点E,BD平分∠ABC,求证:AB=EC.
答案解析
1.【答案】 B
【解析】解:∵四边形ABCD是矩形, ∴AB=CD=2,∠A=∠D=∠DCB=90°,
∵∠DCE=45°,∴DE=DC=2,∴EC=2 2 ,
∵∠DCE=45°,∴∠DEC=45°,∵EB平分∠AEC,
∴∠AEB=∠BEC= 12 ∠AEC= 180°?45°2 =67.5°,∵AD∥BC∴∠AEB=∠EBC,
∴∠BEC=∠EBC,∴BC=CE=2 2 ,∴AD=BC=2 2 ,∴AE=AD-DE=2 2 -2,
故答案为:B.
2.【答案】 A
【解析】解: ∵ 四边形 ABCD 是菱形,
∴OA=OC=12AC , OB=OD=12BD , AC⊥BD ,
∵EF⊥BD 于 F , EG⊥AC 于 G ,
∴ 四边形 EFOG 是矩形, EF//OC , EG//OB ,
∵ 点 E 是线段 BC 的中点,
∴EF 、 EG 都是 △OBC 的中位线,
∴EF=12OC=14AC , EG=12OB=14BD ,
∴ 矩形 EFOG 的面积 =EF×EG=116AC·BD ;
又∵菱形ABCD的面积为= 12AC·BD=24 ,
∴ AC·BD=48
∴矩形 EFOG 的面积= 18×24=3 .
故答案为:A.
3.【答案】 A
【解析】∵在□ABCD中,AE平分∠BAD,
∴∠DAE=∠BAE,∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∵AD=5cm,AB=3cm,
∴BE=3cm,BC=5cm,
∴EC=5-3=2cm,
故答案为:A.
4.【答案】 B
【解析】∵在菱形 ABCD 中,
∴ AC⊥BD ,即:∠AOB=90°,
∴ ∠BEC <90°,
∵ ∠ABC=70° ,
∴∠ABO= 12∠ABC=12×70°=35° ,
∴∠BAO=55°,
∵ ∠BEC =∠BAO+∠ABE,
∴ ∠BEC >55°,
即:55°< ∠BEC <90°.
故答案为:B.
5.【答案】 A
【解析】解:设AF=a(a<2),则F(a,2),E(2,a),
∴FD=DE=2-a,
∴S △DEF =12DF×DE=12(2-a)2=98 ,
解得a=12或72(舍去),
∴k=2a=1,
故答案为:A.
6.【答案】 A
【解析】解:连接OC,
∵∠AOB=90°,CD⊥OA,CE⊥OB,
∴四边形ODCE是矩形,
∴DE=OC=9,
∴ CD=DE2?CE2=9?x2 ,
∵ EH=23DE ,
∴△CEH的面积为 y=23×12×EC×DC=13x×9?x2=13?(x2?812)2+(812)2
当 x2=812 时,△CEH的面积 y 有最大值,最大值为: 13×812=272
故答案为:A.
7.【答案】 245
【解析】解:∵四边形是ABCD菱形,
∴AC⊥BD, OD=12BD=4 , OC=12AC=3 , S菱形ABCD=12AC·BD=12×6×8=24 ,
∴△DOC是直角三角形,
∴ CD=OD2+OC2=5 ,
∵AM⊥CD,
∴ S菱形ABCD=AM·CD ,
∴ AM=245 .
故答案为: 245
8.【答案】 ①②④
【解析】解:连接BE,由折叠可知BO=GO,
∵EG//BF,
∴∠EGO=∠FBO,
在△EOG和△FOB中,
{∠EGO=∠FBO∠EOG=∠FOBBO=GO ,
∴△EOG≌△FOB(AAS) ,
∴EG=BF,
∴四边形EBFG是平行四边形,
由折叠可知BE=EG,
则四边形EBFG为菱形,
故EF⊥BG,GE=GF,
∴①②正确;
∵四边形EBFG为菱形,
过K作kM⊥FG于M,???????????????????????
∴KG平分∠DGH,KD⊥EG,
∴KD=KM,
在Rt△KMH中,KH为斜边,
∴KH > KM=KD,
∴③错误;
当点F与点C重合时,BE=BF=BC=5,AB=3,
在Rt△ABE中,由勾股定理AE= BE2?AB2=52?32=4 ,
∴ED=AD-AE=5-4=1,
在Rt△EDC中,由勾股定理EF= CD2+ED2=32+12=10 ,
∴④正确.
综合,正确的为①②④.
故答案为:①②④.
9.【答案】 证明:∵∠B=∠GDC,
∴DG∥AB,
∴∠1=∠BAD,
∵AD⊥BC,EF⊥BC,
∴AD∥EF,
∴∠2=∠BAD,
∴∠1=∠2.
10.【答案】 证明:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵AD∥BC,
∴∠ADB=∠CBD,
∴∠ABD=∠ADB,
∴AB=AD,
∵AD∥CE AE∥CD,
∴四边形AECD是平行四边形,
∴AD=CE,
∵AD=AB.
∴AB=CE.
