勾股定理
图片预览




文档简介
(共20张PPT)
14.1勾股定理(4)
1、在Rt△ABC中,∠C=90°,
①若a=5,b=12,则c=______;
②若c=61,b=60,则a=_____;
③若a∶b=3∶4,c=10则 SRt△ABC=_____。
13
11
24
基础过关
勾股定理的应用
当今世界上许多科学家正在试探着寻找“外星人”,人们为了与外星人取得联系,想了很多办法。我国数学家华罗庚也曾提出,若要沟通两个不同星球之间的信息交流,最好在太空飞船中带去这样的图形。
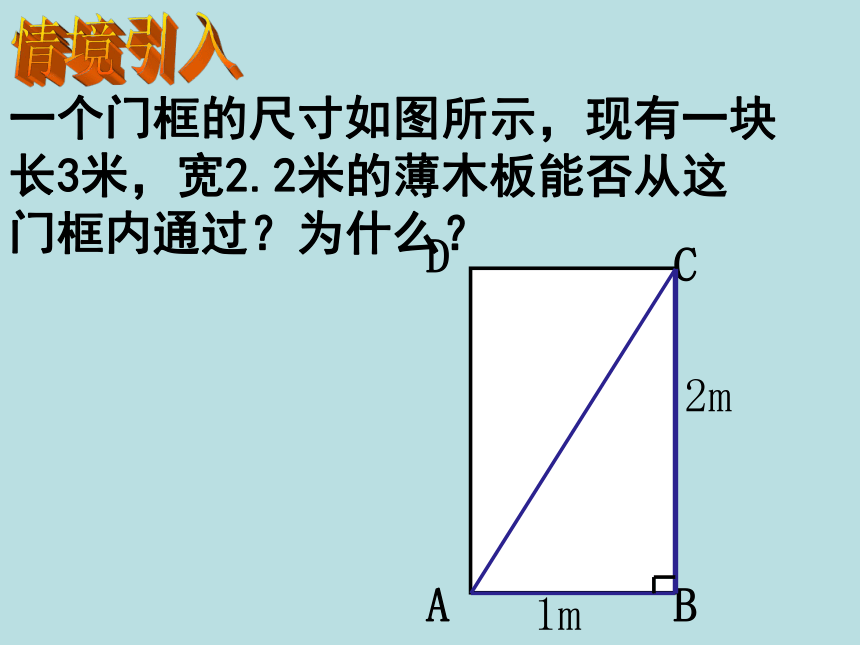
一个门框的尺寸如图所示,现有一块长3米,宽2.2米的薄木板能否从这门框内通过?为什么?
A
C
B
D
1m
2m
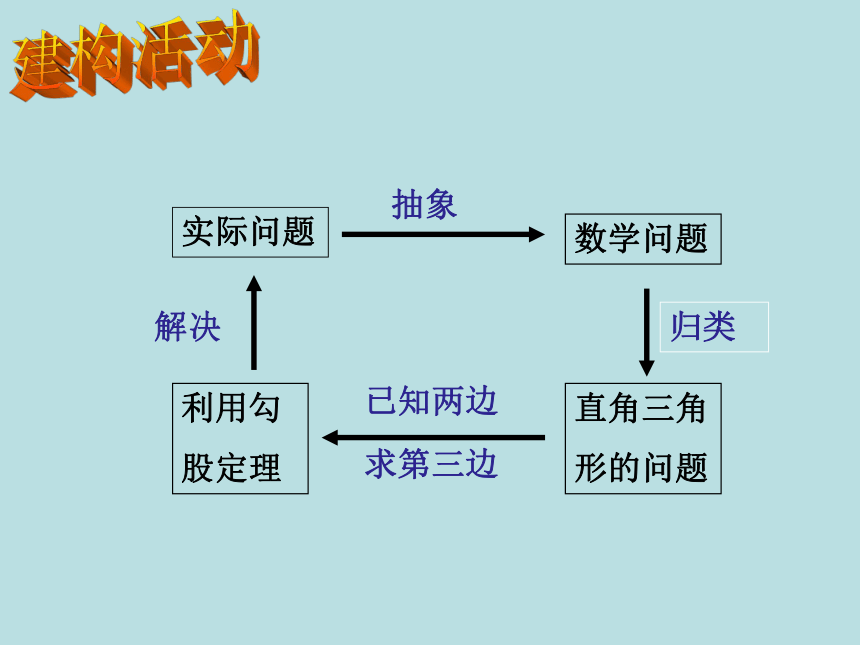
实际问题
直角三角
形的问题
数学问题
利用勾
股定理
已知两边
求第三边
抽象
归类
解决
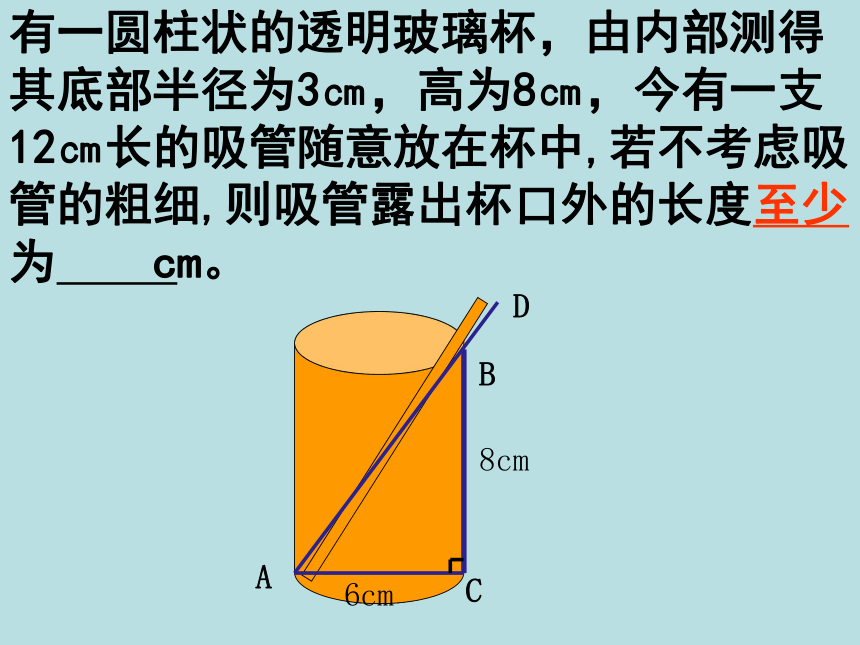
有一圆柱状的透明玻璃杯,由内部测得其底部半径为3㎝,高为8㎝,今有一支12㎝长的吸管随意放在杯中,若不考虑吸管的粗细,则吸管露出杯口外的长度至少为 cm。
A
C
B
D
6cm
8cm
例2.如图一个5米长的梯子AB,斜靠在
一竖直的墙AO上,这时AO的距离为4
米,如果将梯子的顶端A沿墙下滑2米,
那么梯子的底端也外移2米吗?
B
A
C
D
O
巩固
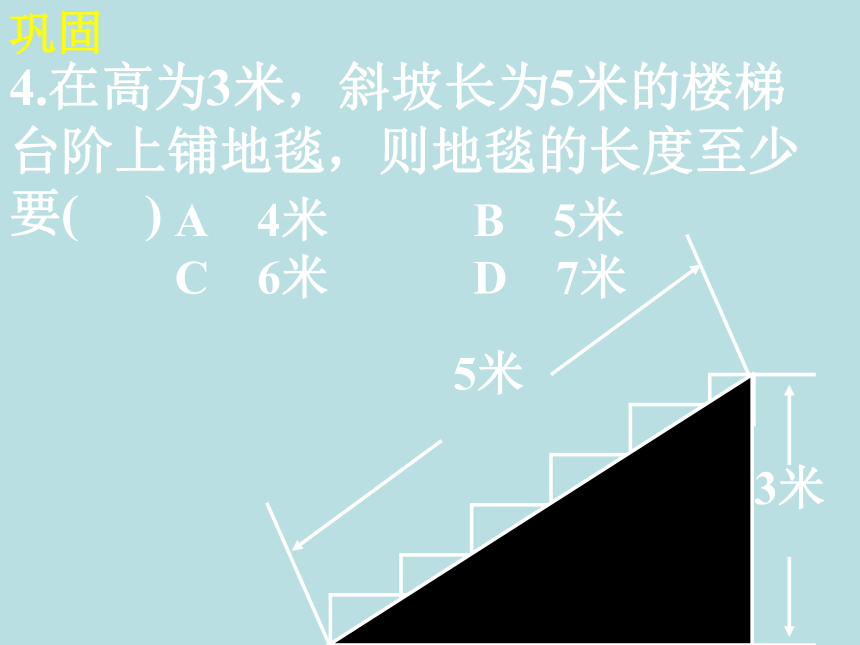
4.在高为3米,斜坡长为5米的楼梯台阶上铺地毯,则地毯的长度至少要( )
A 4米 B 5米
C 6米 D 7米
3米
5米
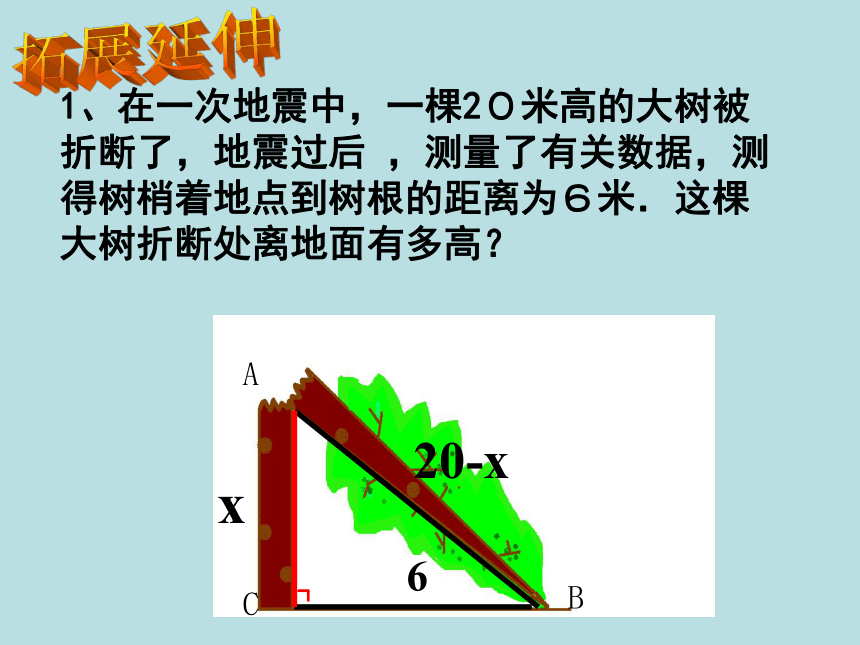
1、在一次地震中,一棵20米高的大树被折断了,地震过后 ,测量了有关数据,测得树梢着地点到树根的距离为6米.这棵大树折断处离地面有多高?
A
C
B
6
x
20-x
与古人比一比
6、 在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
A
D
B
C
x
1
X+1
5
A
B
我怎么走
会最近呢
1.有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B , 蚂蚁沿着圆柱侧面爬行的最短路程是多少 (π的值取3)
B
A
高
12cm
B
A
长18cm (π的值取3)
9cm
∵ AB2=92+122=81+144=225=
∴ AB=15(cm)
答:蚂蚁爬行的最短路程是15厘米.
152
解:将圆柱如图侧面展开.在Rt△ABC中,根据勾股定理
C
巩固
2.如图,以A点环绕油罐建梯子,使它正好落到A点的正上方B点处,问梯子最短要多少米?(已知油罐底面周长为12m,AB为5m)
A
B
1.如图,将一根25㎝长的细木棒放入长、宽、高分别为8㎝、6㎝和10㎝的长方体无盖盒子中,则细木棒露在盒外面的最短长度是多少㎝.(保留1位小数)
A
B
C
D
实际问题
直角三角
形的问题
数学问题
利用勾
股定理
已知两边求第三边
抽象
归类
解决
已知一边设未知数列方程
1、课本10页: 4 、 5、 10
2、课堂练习:4页:
A
C
B
A’
C’
0.4m
(
梯子长度不变
2)如果梯子上端A向下滑动0.4米到A′处,则
梯子的底端C向C′是否也滑动了0.4米,如果是,
请说明理由;如果不是,请说出滑动了多少米?
实际应用
5、如图,将长为2.5米的梯子AC斜靠在墙上,
BC长为0.7米,
求:(1)梯子上端A到墙的底端B的距离AB。
滑动时,三角形的面积不变,对吗?
8m
2m
8m
A
B
C
实际应用
2、有两棵树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了( )
A.7m B.8m C.9m D.10m
3、如图所示,要修一个种植蔬菜的育苗大棚,棚宽a=2m,高b=1.5m,长d=12m,则修盖在顶上的塑料薄膜需要的面积为多少
a
b
c
d
帮一帮农民
4、一大楼发生火灾,消防车立即赶到距大楼9米处,升起云梯到失火的窗口,已知发生火灾的窗口距地面有14.2米,云梯底部距地面2.2米,问云梯至少需要搭出多少米可以够到失火的窗口
A
B
C
E
D
帮一帮消防员
14.1勾股定理(4)
1、在Rt△ABC中,∠C=90°,
①若a=5,b=12,则c=______;
②若c=61,b=60,则a=_____;
③若a∶b=3∶4,c=10则 SRt△ABC=_____。
13
11
24
基础过关
勾股定理的应用
当今世界上许多科学家正在试探着寻找“外星人”,人们为了与外星人取得联系,想了很多办法。我国数学家华罗庚也曾提出,若要沟通两个不同星球之间的信息交流,最好在太空飞船中带去这样的图形。
一个门框的尺寸如图所示,现有一块长3米,宽2.2米的薄木板能否从这门框内通过?为什么?
A
C
B
D
1m
2m
实际问题
直角三角
形的问题
数学问题
利用勾
股定理
已知两边
求第三边
抽象
归类
解决
有一圆柱状的透明玻璃杯,由内部测得其底部半径为3㎝,高为8㎝,今有一支12㎝长的吸管随意放在杯中,若不考虑吸管的粗细,则吸管露出杯口外的长度至少为 cm。
A
C
B
D
6cm
8cm
例2.如图一个5米长的梯子AB,斜靠在
一竖直的墙AO上,这时AO的距离为4
米,如果将梯子的顶端A沿墙下滑2米,
那么梯子的底端也外移2米吗?
B
A
C
D
O
巩固
4.在高为3米,斜坡长为5米的楼梯台阶上铺地毯,则地毯的长度至少要( )
A 4米 B 5米
C 6米 D 7米
3米
5米
1、在一次地震中,一棵20米高的大树被折断了,地震过后 ,测量了有关数据,测得树梢着地点到树根的距离为6米.这棵大树折断处离地面有多高?
A
C
B
6
x
20-x
与古人比一比
6、 在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
A
D
B
C
x
1
X+1
5
A
B
我怎么走
会最近呢
1.有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B , 蚂蚁沿着圆柱侧面爬行的最短路程是多少 (π的值取3)
B
A
高
12cm
B
A
长18cm (π的值取3)
9cm
∵ AB2=92+122=81+144=225=
∴ AB=15(cm)
答:蚂蚁爬行的最短路程是15厘米.
152
解:将圆柱如图侧面展开.在Rt△ABC中,根据勾股定理
C
巩固
2.如图,以A点环绕油罐建梯子,使它正好落到A点的正上方B点处,问梯子最短要多少米?(已知油罐底面周长为12m,AB为5m)
A
B
1.如图,将一根25㎝长的细木棒放入长、宽、高分别为8㎝、6㎝和10㎝的长方体无盖盒子中,则细木棒露在盒外面的最短长度是多少㎝.(保留1位小数)
A
B
C
D
实际问题
直角三角
形的问题
数学问题
利用勾
股定理
已知两边求第三边
抽象
归类
解决
已知一边设未知数列方程
1、课本10页: 4 、 5、 10
2、课堂练习:4页:
A
C
B
A’
C’
0.4m
(
梯子长度不变
2)如果梯子上端A向下滑动0.4米到A′处,则
梯子的底端C向C′是否也滑动了0.4米,如果是,
请说明理由;如果不是,请说出滑动了多少米?
实际应用
5、如图,将长为2.5米的梯子AC斜靠在墙上,
BC长为0.7米,
求:(1)梯子上端A到墙的底端B的距离AB。
滑动时,三角形的面积不变,对吗?
8m
2m
8m
A
B
C
实际应用
2、有两棵树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了( )
A.7m B.8m C.9m D.10m
3、如图所示,要修一个种植蔬菜的育苗大棚,棚宽a=2m,高b=1.5m,长d=12m,则修盖在顶上的塑料薄膜需要的面积为多少
a
b
c
d
帮一帮农民
4、一大楼发生火灾,消防车立即赶到距大楼9米处,升起云梯到失火的窗口,已知发生火灾的窗口距地面有14.2米,云梯底部距地面2.2米,问云梯至少需要搭出多少米可以够到失火的窗口
A
B
C
E
D
帮一帮消防员
