矩形
图片预览


文档简介
(共16张PPT)
§19.2.1 矩形
人教版八年级下册第十九章
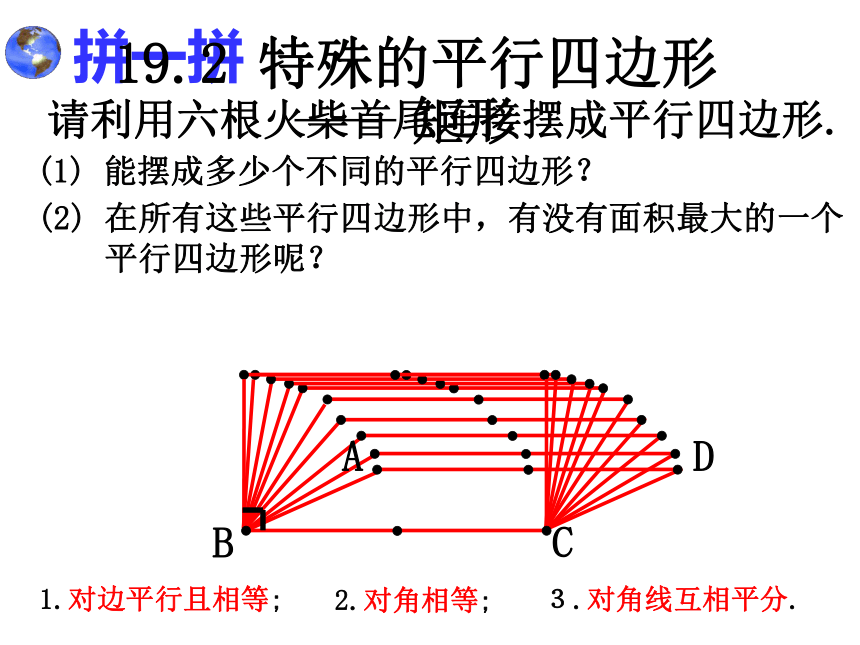
拼一拼
请利用六根火柴首尾连接摆成平行四边形.
(1) 能摆成多少个不同的平行四边形?
A
C
B
D
(2) 在所有这些平行四边形中,有没有面积最大的一个
平行四边形呢?
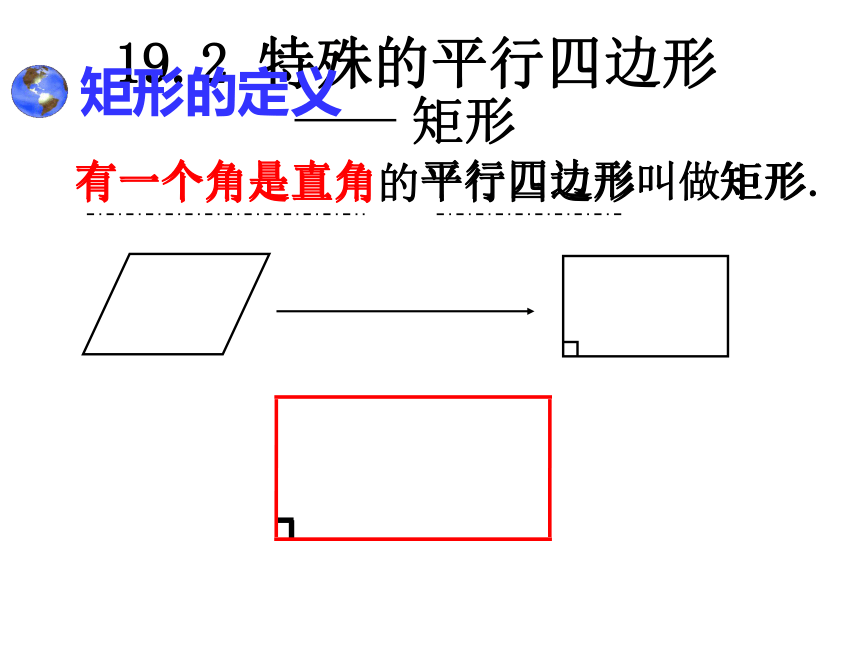
19.2 特殊的平行四边形
矩形
1.对边平行且相等;
2.对角相等;
3.对角线互相平分.
平行四边形
19.2 特殊的平行四边形
有一个角是直角的平行四边形
矩形的定义
叫做矩形.
矩形
有一个角是直角
矩形
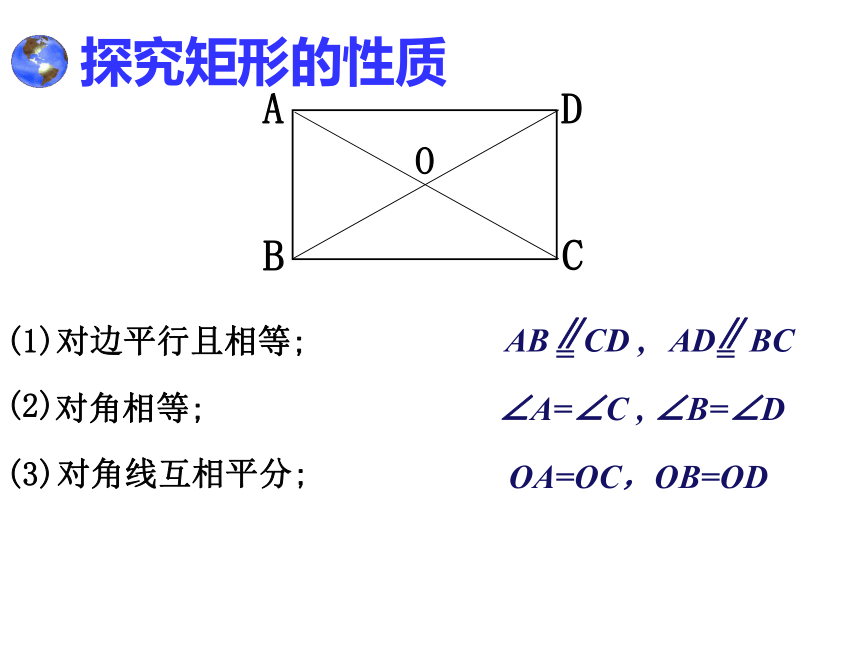
探究矩形的性质
A
C
B
D
O
(1)对边平行且相等;
(2)
(3)
AB CD ,
=
∥
AD BC
=
∥
∠A=∠C , ∠B=∠D
OA=OC,OB=OD
对角相等;
对角线互相平分;
OA=OC,OB=OD
OA=OC=OB=OD
∠BAD=∠BCD =∠ABC=∠ADC= 90°
矩形的性质
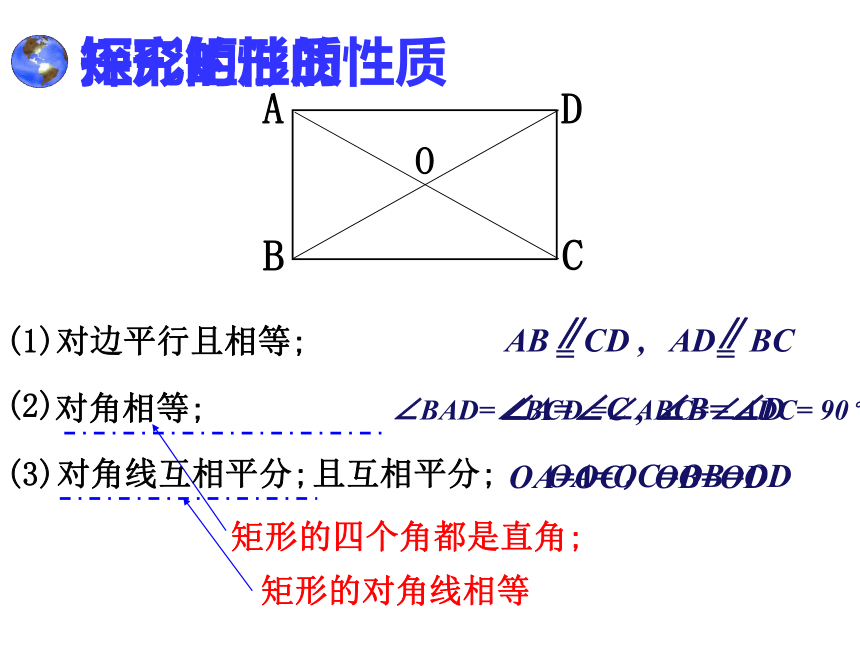
探究矩形的性质
A
C
B
D
O
(1)对边平行且相等;
(2)
(3)
AB CD ,
=
∥
AD BC
=
∥
∠A=∠C , ∠B=∠D
矩形的四个角都是直角;
矩形的对角线相等
对角相等;
对角线互相平分;
且互相平分;
试一试
1.矩形具有而一般平行四边形不具有的性
质是……………………………( )
A.对角相等 B.对边相等
C.对角线相等 D.对角线互相平分
C
试一试
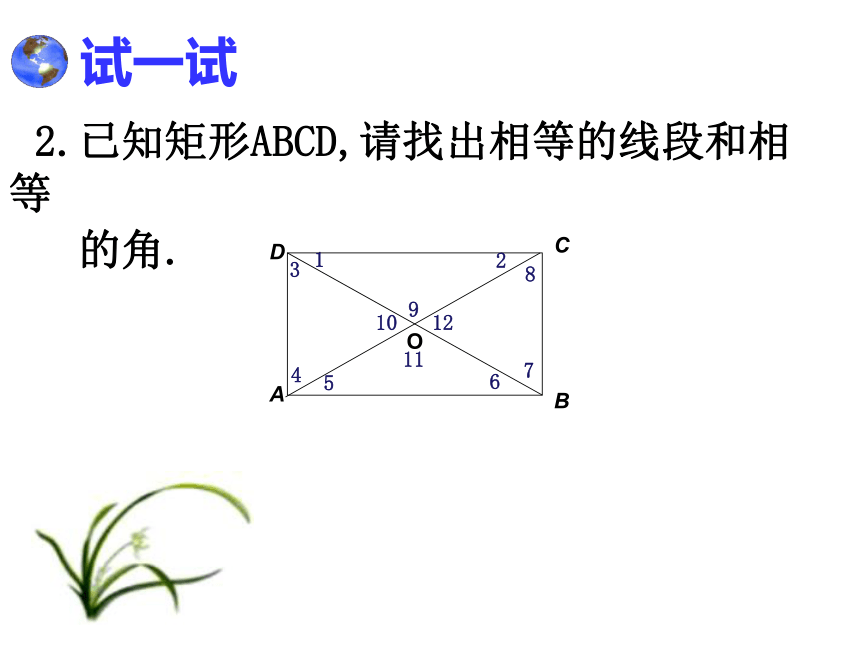
2.已知矩形ABCD,请找出相等的线段和相等
的角.
A
B
C
D
O
1
2
3
4
5
6
7
8
9
10
11
12
共同练习
如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4cm,求矩形对角线的长.
B
C
D
A
O
矩形的问题可以转化到直角三角形或等腰(边)三角形的问题来解决.
投圈游戏
三位学生正在做投圈游戏,他们分别站在一个直角三角形的三个顶点处,目标物放在斜边的中点处,这样的队形对每个人公平吗
O
A
B
C
在直角三角形中斜边上的中线等于斜边的一半.
D
A
B
C
O
A
B
C
O
练一练
D
C
B
A
┓
已知△ABC是Rt△,∠ABC=900,BD是斜边AC上的中线.
(1)若BD=3㎝,则AC=______ ㎝;
(2)若∠C=30°,AB=5㎝,则AC=_____㎝,
BD=_____㎝.
6
5
10
用一用
某学校因地制宜:先向北量6m,再向东量8m,接着向南量6m,最后向西量8m,在圈出的这块空地上建一个草坪.
(1)圈出的空地是什么形状
(2)考虑到护理草坪,学校购置了一台自动喷水器, 这台机器的最大喷水距离为5m,问这台机器能对整个草坪进行护理吗 若能,则喷水器应安放在何处;若不能,请说明理由.
1.有一个角是直角的平行四边形是矩形.
A
B
C
D
O
2.矩形的性质
矩形的四个角均为直角
矩形的对角线互相平分且相等
矩形的对边平行且相等
3.直角三角形斜边上的中线等于斜边的
一半.
北
西
东
南
6
8
6
8
(3)直角三角形的一个重要性质:斜边上的中线
等于斜边的一半;
(1)矩形定义:
有一个角是直角的平行四边形叫矩形
矩形的对边平行且相等
矩形的四个角均为直角
(2)矩形
矩形的对角线互相平分且相等
课堂小结
1.知识小结
2.学法小结
(1)用类比的方法探究矩形的性质,先找共性再找特殊性,
并注意性质的整合;
(2)矩形的问题常可以转化为直角三角形或等腰三角形
的问题来解决.
(必做题)作业本习题;
(备选题)矩形ABCD中,AB= 4,BC=2,E是边CD
上的一点,AE=AB.求∠BEC的度数.
A
B
C
D
E
课后作业
脸蛋方方是矩形,例如黑板和窗门。
对角线段皆相等,相互交叉且平分。
内有直角三角形,斜边中线半斜边。
若要牢记其定义,直角平行四边形。
矩形之歌
再见
探究矩形的性质
A
C
B
D
O
A
C
B
D
O
观察由平行四边形变到矩形的过程,对角线与内角发生了什么变化?从而你还能发现矩形的什么性质呢
§19.2.1 矩形
人教版八年级下册第十九章
拼一拼
请利用六根火柴首尾连接摆成平行四边形.
(1) 能摆成多少个不同的平行四边形?
A
C
B
D
(2) 在所有这些平行四边形中,有没有面积最大的一个
平行四边形呢?
19.2 特殊的平行四边形
矩形
1.对边平行且相等;
2.对角相等;
3.对角线互相平分.
平行四边形
19.2 特殊的平行四边形
有一个角是直角的平行四边形
矩形的定义
叫做矩形.
矩形
有一个角是直角
矩形
探究矩形的性质
A
C
B
D
O
(1)对边平行且相等;
(2)
(3)
AB CD ,
=
∥
AD BC
=
∥
∠A=∠C , ∠B=∠D
OA=OC,OB=OD
对角相等;
对角线互相平分;
OA=OC,OB=OD
OA=OC=OB=OD
∠BAD=∠BCD =∠ABC=∠ADC= 90°
矩形的性质
探究矩形的性质
A
C
B
D
O
(1)对边平行且相等;
(2)
(3)
AB CD ,
=
∥
AD BC
=
∥
∠A=∠C , ∠B=∠D
矩形的四个角都是直角;
矩形的对角线相等
对角相等;
对角线互相平分;
且互相平分;
试一试
1.矩形具有而一般平行四边形不具有的性
质是……………………………( )
A.对角相等 B.对边相等
C.对角线相等 D.对角线互相平分
C
试一试
2.已知矩形ABCD,请找出相等的线段和相等
的角.
A
B
C
D
O
1
2
3
4
5
6
7
8
9
10
11
12
共同练习
如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4cm,求矩形对角线的长.
B
C
D
A
O
矩形的问题可以转化到直角三角形或等腰(边)三角形的问题来解决.
投圈游戏
三位学生正在做投圈游戏,他们分别站在一个直角三角形的三个顶点处,目标物放在斜边的中点处,这样的队形对每个人公平吗
O
A
B
C
在直角三角形中斜边上的中线等于斜边的一半.
D
A
B
C
O
A
B
C
O
练一练
D
C
B
A
┓
已知△ABC是Rt△,∠ABC=900,BD是斜边AC上的中线.
(1)若BD=3㎝,则AC=______ ㎝;
(2)若∠C=30°,AB=5㎝,则AC=_____㎝,
BD=_____㎝.
6
5
10
用一用
某学校因地制宜:先向北量6m,再向东量8m,接着向南量6m,最后向西量8m,在圈出的这块空地上建一个草坪.
(1)圈出的空地是什么形状
(2)考虑到护理草坪,学校购置了一台自动喷水器, 这台机器的最大喷水距离为5m,问这台机器能对整个草坪进行护理吗 若能,则喷水器应安放在何处;若不能,请说明理由.
1.有一个角是直角的平行四边形是矩形.
A
B
C
D
O
2.矩形的性质
矩形的四个角均为直角
矩形的对角线互相平分且相等
矩形的对边平行且相等
3.直角三角形斜边上的中线等于斜边的
一半.
北
西
东
南
6
8
6
8
(3)直角三角形的一个重要性质:斜边上的中线
等于斜边的一半;
(1)矩形定义:
有一个角是直角的平行四边形叫矩形
矩形的对边平行且相等
矩形的四个角均为直角
(2)矩形
矩形的对角线互相平分且相等
课堂小结
1.知识小结
2.学法小结
(1)用类比的方法探究矩形的性质,先找共性再找特殊性,
并注意性质的整合;
(2)矩形的问题常可以转化为直角三角形或等腰三角形
的问题来解决.
(必做题)作业本习题;
(备选题)矩形ABCD中,AB= 4,BC=2,E是边CD
上的一点,AE=AB.求∠BEC的度数.
A
B
C
D
E
课后作业
脸蛋方方是矩形,例如黑板和窗门。
对角线段皆相等,相互交叉且平分。
内有直角三角形,斜边中线半斜边。
若要牢记其定义,直角平行四边形。
矩形之歌
再见
探究矩形的性质
A
C
B
D
O
A
C
B
D
O
观察由平行四边形变到矩形的过程,对角线与内角发生了什么变化?从而你还能发现矩形的什么性质呢
