19.2.2一次函数图像与性质提升复习-2020-2021学年人教版八年级数学下册培优训练(Word版 含答案)
文档属性
| 名称 | 19.2.2一次函数图像与性质提升复习-2020-2021学年人教版八年级数学下册培优训练(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 229.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 09:15:28 | ||
图片预览


文档简介
一次函数图象和性质练习与反馈:
练习一:
1、函数y=3x-6的图象中:
(1)随着x的增大,y将 (填“增大”或“减小”)
(2)它的图象从左到右 (填“上升”或“下降”)
(3)图象与x轴的交点坐标是 ,与y轴的交点坐标是
2、已知函数y=(m-3)x-false.
当m取何值时,y随x的增大而增大?
当m取何值时,y随x的增大而减小?
3、直线y=4x-2与x轴的交点坐标是 ,与y轴的交点坐标是
4、直线y=false与x轴的交点坐标是 ,与y轴的交点坐标是
5、写出一条与直线y=2x-3平行的直线
6、写出一条与直线y=2x-3平行,且经过点(2,7)的直线
7、直线y=-5x+7可以看作是由直线y=-5x-1向 平移 个单位得到的
8. 已知函数轴交点的纵坐标为,且当,则此函数的解析式为 .
9. 在函数中,函数随着的增大而 ,此函数的图象经过点,则 .
10. 如图,表示一次函数与正比例函数(为常数,且
)图象的是( )
13335078105O
x
y
x
y
O
x
y
O
x
y
O
A.
B.
C.
D.
O
x
y
x
y
O
x
y
O
x
y
O
A.
B.
C.
D.
11. 在下列四个函数中,的值随值的增大而减小的是( )
A. B. C. D.
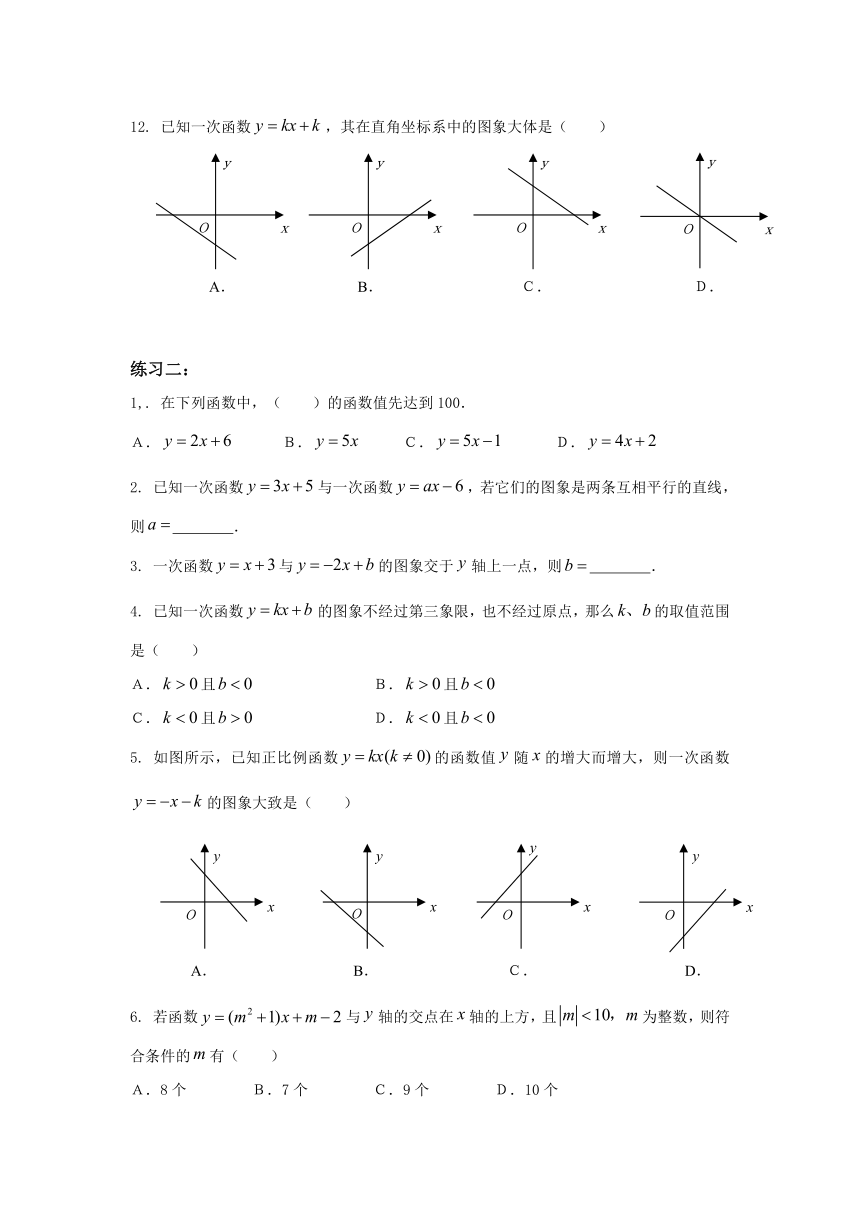
12. 已知一次函数,其在直角坐标系中的图象大体是( )
2286000O
y
x
O
y
x
O
y
x
O
y
x
D.
C.
B.
A.
O
y
x
O
y
x
O
y
x
O
y
x
D.
C.
B.
A.
练习二:
1,. 在下列函数中,( )的函数值先达到100.
A. B. C. D.
2. 已知一次函数与一次函数,若它们的图象是两条互相平行的直线,则 .
3. 一次函数与的图象交于轴上一点,则 .
4. 已知一次函数的图象不经过第三象限,也不经过原点,那么的取值范围是( )
A.且 B.且
C.且 D.且
5. 如图所示,已知正比例函数的函数值随的增大而增大,则一次函数的图象大致是( )
26670070485O
x
y
O
x
y
O
x
y
O
x
y
D.
C.
B.
A.
O
x
y
O
x
y
O
x
y
O
x
y
D.
C.
B.
A.
6. 若函数与轴的交点在轴的上方,且为整数,则符合条件的有( )
A.8个 B.7个 C.9个 D.10个
函数,随的增大而 .
8. 已知一次函数的图象经过一、二、四象限,求的取值范围.
9.如图,A、B分别是x轴上位于原点左右两侧的点,点P(2,p)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,△AOP的面积为6;
335534033655(1)求△COP的面积;
(2)求点A的坐标及p的值;
(3)若△BOP与△DOP的面积相等,求直线BD的函数解析式。
一次函数图象和性质练习与反馈:
练习一:
1、函数y=3x-6的图象中:
(1)随着x的增大,y将 (填“增大”或“减小”)
(2)它的图象从左到右 (填“上升”或“下降”)
(3)图象与x轴的交点坐标是 ,与y轴的交点坐标是
答案:增大;上升;(2,0);(0,-6)
2、已知函数y=(m-3)x-false.
当m取何值时,y随x的增大而增大?
当m取何值时,y随x的增大而减小?
答案:m>3;m<3
3、直线y=4x-2与x轴的交点坐标是 ,与y轴的交点坐标是
答案:(12,0);(0,-2)
4、直线y=false与x轴的交点坐标是 ,与y轴的交点坐标是
答案:(3,0);(0,-2)
5、写出一条与直线y=2x-3平行的直线
答案:y=2x(k值相同均可)
6、写出一条与直线y=2x-3平行,且经过点(2,7)的直线
答案:y=2x+3
7、直线y=-5x+7可以看作是由直线y=-5x-1向 平移 个单位得到的
答案:下;8
8. 已知函数轴交点的纵坐标为,且当,则此函数的解析式为 .
答案:y=7x-5
9. 在函数中,函数随着的增大而 ,此函数的图象经过点,则 .
答案:增大;5
10. 如图,表示一次函数与正比例函数(为常数,且
)图象的是( )
13335078105O
x
y
x
y
O
x
y
O
x
y
O
A.
B.
C.
D.
O
x
y
x
y
O
x
y
O
x
y
O
A.
B.
C.
D.
答案:A
11. 在下列四个函数中,的值随值的增大而减小的是( )
A. B. C. D.
答案:C
12. 已知一次函数,其在直角坐标系中的图象大体是( )
2286000O
y
x
O
y
x
O
y
x
O
y
x
D.
C.
B.
A.
O
y
x
O
y
x
O
y
x
O
y
x
D.
C.
B.
A.
答案:A
练习二:
1,. 在下列函数中,( )的函数值先达到100.
A. B. C. D.
答案:B
2. 已知一次函数与一次函数,若它们的图象是两条互相平行的直线,则 .
答案:3
3. 一次函数与的图象交于轴上一点,则 .
答案:3
4. 已知一次函数的图象不经过第三象限,也不经过原点,那么的取值范围是( )
A.且 B.且
C.且 D.且
答案:C
5. 如图所示,已知正比例函数的函数值随的增大而增大,则一次函数的图象大致是( )
26670070485O
x
y
O
x
y
O
x
y
O
x
y
D.
C.
B.
A.
O
x
y
O
x
y
O
x
y
O
x
y
D.
C.
B.
A.
答案:B
6. 若函数与轴的交点在轴的上方,且为整数,则符合条件的有( )
A.8个 B.7个 C.9个 D.10个
答案:B
函数,随的增大而 .
答案:减小
8. 已知一次函数的图象经过一、二、四象限,求的取值范围.
解:由题意可得:m-3<0;2m-1>0
∴解得m<3;m>12
∴12<m<3
9.如图,A、B分别是x轴上位于原点左右两侧的点,点P(2,p)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,△AOP的面积为6;
335534033655(1)求△COP的面积;
(2)求点A的坐标及p的值;
(3)若△BOP与△DOP的面积相等,求直线BD的函数解析式。
解:(1)作PE⊥y轴于E,
∵P的横坐标是2,则PE=2.
∴S△COP=12OC×PE=12×2×2=2;
2)∵S△AOC=S△AOP-S△COP=6-2=4,
∴S△AOC=12OA×OC=4,即
12×OA×2=4,
∴OA=4,
∴A的坐标是(-4,0).
设直线AP的解析式是y=kx+b,则
0=?4k+b2=b,
解得:
k=12b=2.
则直线的解析式是y=12x+2.
当x=2时,y=3,即p=3;
(3)∵S△AOP=S△BOP,
∴OB=OA=4,则B的坐标是(4,0),
设直线BD的解析式是y=mx+n,则0=4m+n3=2m+n,
,
解得m=?32n=6,
∴y=?32x+6
练习一:
1、函数y=3x-6的图象中:
(1)随着x的增大,y将 (填“增大”或“减小”)
(2)它的图象从左到右 (填“上升”或“下降”)
(3)图象与x轴的交点坐标是 ,与y轴的交点坐标是
2、已知函数y=(m-3)x-false.
当m取何值时,y随x的增大而增大?
当m取何值时,y随x的增大而减小?
3、直线y=4x-2与x轴的交点坐标是 ,与y轴的交点坐标是
4、直线y=false与x轴的交点坐标是 ,与y轴的交点坐标是
5、写出一条与直线y=2x-3平行的直线
6、写出一条与直线y=2x-3平行,且经过点(2,7)的直线
7、直线y=-5x+7可以看作是由直线y=-5x-1向 平移 个单位得到的
8. 已知函数轴交点的纵坐标为,且当,则此函数的解析式为 .
9. 在函数中,函数随着的增大而 ,此函数的图象经过点,则 .
10. 如图,表示一次函数与正比例函数(为常数,且
)图象的是( )
13335078105O
x
y
x
y
O
x
y
O
x
y
O
A.
B.
C.
D.
O
x
y
x
y
O
x
y
O
x
y
O
A.
B.
C.
D.
11. 在下列四个函数中,的值随值的增大而减小的是( )
A. B. C. D.
12. 已知一次函数,其在直角坐标系中的图象大体是( )
2286000O
y
x
O
y
x
O
y
x
O
y
x
D.
C.
B.
A.
O
y
x
O
y
x
O
y
x
O
y
x
D.
C.
B.
A.
练习二:
1,. 在下列函数中,( )的函数值先达到100.
A. B. C. D.
2. 已知一次函数与一次函数,若它们的图象是两条互相平行的直线,则 .
3. 一次函数与的图象交于轴上一点,则 .
4. 已知一次函数的图象不经过第三象限,也不经过原点,那么的取值范围是( )
A.且 B.且
C.且 D.且
5. 如图所示,已知正比例函数的函数值随的增大而增大,则一次函数的图象大致是( )
26670070485O
x
y
O
x
y
O
x
y
O
x
y
D.
C.
B.
A.
O
x
y
O
x
y
O
x
y
O
x
y
D.
C.
B.
A.
6. 若函数与轴的交点在轴的上方,且为整数,则符合条件的有( )
A.8个 B.7个 C.9个 D.10个
函数,随的增大而 .
8. 已知一次函数的图象经过一、二、四象限,求的取值范围.
9.如图,A、B分别是x轴上位于原点左右两侧的点,点P(2,p)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,△AOP的面积为6;
335534033655(1)求△COP的面积;
(2)求点A的坐标及p的值;
(3)若△BOP与△DOP的面积相等,求直线BD的函数解析式。
一次函数图象和性质练习与反馈:
练习一:
1、函数y=3x-6的图象中:
(1)随着x的增大,y将 (填“增大”或“减小”)
(2)它的图象从左到右 (填“上升”或“下降”)
(3)图象与x轴的交点坐标是 ,与y轴的交点坐标是
答案:增大;上升;(2,0);(0,-6)
2、已知函数y=(m-3)x-false.
当m取何值时,y随x的增大而增大?
当m取何值时,y随x的增大而减小?
答案:m>3;m<3
3、直线y=4x-2与x轴的交点坐标是 ,与y轴的交点坐标是
答案:(12,0);(0,-2)
4、直线y=false与x轴的交点坐标是 ,与y轴的交点坐标是
答案:(3,0);(0,-2)
5、写出一条与直线y=2x-3平行的直线
答案:y=2x(k值相同均可)
6、写出一条与直线y=2x-3平行,且经过点(2,7)的直线
答案:y=2x+3
7、直线y=-5x+7可以看作是由直线y=-5x-1向 平移 个单位得到的
答案:下;8
8. 已知函数轴交点的纵坐标为,且当,则此函数的解析式为 .
答案:y=7x-5
9. 在函数中,函数随着的增大而 ,此函数的图象经过点,则 .
答案:增大;5
10. 如图,表示一次函数与正比例函数(为常数,且
)图象的是( )
13335078105O
x
y
x
y
O
x
y
O
x
y
O
A.
B.
C.
D.
O
x
y
x
y
O
x
y
O
x
y
O
A.
B.
C.
D.
答案:A
11. 在下列四个函数中,的值随值的增大而减小的是( )
A. B. C. D.
答案:C
12. 已知一次函数,其在直角坐标系中的图象大体是( )
2286000O
y
x
O
y
x
O
y
x
O
y
x
D.
C.
B.
A.
O
y
x
O
y
x
O
y
x
O
y
x
D.
C.
B.
A.
答案:A
练习二:
1,. 在下列函数中,( )的函数值先达到100.
A. B. C. D.
答案:B
2. 已知一次函数与一次函数,若它们的图象是两条互相平行的直线,则 .
答案:3
3. 一次函数与的图象交于轴上一点,则 .
答案:3
4. 已知一次函数的图象不经过第三象限,也不经过原点,那么的取值范围是( )
A.且 B.且
C.且 D.且
答案:C
5. 如图所示,已知正比例函数的函数值随的增大而增大,则一次函数的图象大致是( )
26670070485O
x
y
O
x
y
O
x
y
O
x
y
D.
C.
B.
A.
O
x
y
O
x
y
O
x
y
O
x
y
D.
C.
B.
A.
答案:B
6. 若函数与轴的交点在轴的上方,且为整数,则符合条件的有( )
A.8个 B.7个 C.9个 D.10个
答案:B
函数,随的增大而 .
答案:减小
8. 已知一次函数的图象经过一、二、四象限,求的取值范围.
解:由题意可得:m-3<0;2m-1>0
∴解得m<3;m>12
∴12<m<3
9.如图,A、B分别是x轴上位于原点左右两侧的点,点P(2,p)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,△AOP的面积为6;
335534033655(1)求△COP的面积;
(2)求点A的坐标及p的值;
(3)若△BOP与△DOP的面积相等,求直线BD的函数解析式。
解:(1)作PE⊥y轴于E,
∵P的横坐标是2,则PE=2.
∴S△COP=12OC×PE=12×2×2=2;
2)∵S△AOC=S△AOP-S△COP=6-2=4,
∴S△AOC=12OA×OC=4,即
12×OA×2=4,
∴OA=4,
∴A的坐标是(-4,0).
设直线AP的解析式是y=kx+b,则
0=?4k+b2=b,
解得:
k=12b=2.
则直线的解析式是y=12x+2.
当x=2时,y=3,即p=3;
(3)∵S△AOP=S△BOP,
∴OB=OA=4,则B的坐标是(4,0),
设直线BD的解析式是y=mx+n,则0=4m+n3=2m+n,
,
解得m=?32n=6,
∴y=?32x+6
