第9章 中心对称图形 单元测试-2020-2021学年苏科版八年级数学下册(Word版 含答案)
文档属性
| 名称 | 第9章 中心对称图形 单元测试-2020-2021学年苏科版八年级数学下册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 667.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 09:17:17 | ||
图片预览




文档简介
八下中心对称图形单元测试
一、单选题(1-10题,每题3分,共30分)
1.下列图案中既是中心对称图形,又是轴对称图形的是( )
A. B. C. D.
2.在四边形false中,给出下列条件:①false;②false;③false;④false.从以上选择两个条件使四边形false为平行四边形的选法有( )
A.3种 B.4种 C.5种 D.6种
3.如图:在平行四边形ABCD中,AB=5,AD=10,BF=3,过BC的中点E作EF⊥AB,垂足为点F.连接DF,求DF的长( )
A.10 B.9 C.8false D.7false
4.如图,在等边△ABC中,BC=8cm,射线AGfalseBC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以3cm/s的速度运动.设运动时间为t(s),当t=( )s时,以A、C、E、F为顶点的四边形是平行四边形.
A.1或2 B.2 C.2或3 D.2或4
5.如图,点E是△ABC内一点,∠AEB=90°,AE平分∠BAC,D是边AB的中点,延长线段DE交边BC于点F,若AB=6,EF=1,则线段AC的长为( )
A.7 B.false C.8 D.9
6.如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F.将△DEF沿EF折叠,点D恰好落在BE上的M点处,延长BC,EF交于点N,下列四个结论不正确的是( )
A.DF=CF B.BF⊥EN
C.△BEN是等边三角形 D.S△BEF=3S△DEF
7.如图,在四边形false中,E,F分别为false、false的中点,G是false的中点,则false与false的关系是( )
A.false B.false C.false D.不确定
8.如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
A.2 B.2false C.3 D.4
9.如图,在四边形ABCD中,AC=BD=6,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2的值为( )
A.9 B.18 C.36 D.48
10.如图,在false中,false,点false分别是边false上的动点,连接false,点false分别为false的中点,连接false,则false的最小值为( ).
A.false B.false C.false D.1
二、填空题(11-18题,每题2分,共16分)
11.若点false和false关于原点对称,则false的值是___________.
12.如图,平行四边形false中,false、false相交于点false,若false,则false的周长为________.
13.如图,平行四边形false的对角线相较于点false,且false,过false作false,交false于点false,若平行四边形false的周长为false,则false的周长为______false.
14.在平面直角坐标系中,已知平行四边形的三个顶点坐标分别是false,则平行四边形第四个顶点D的坐标为__________.
15.已知平行四边形false中,点false和点false分别是边false和false上的点,false,false,将false沿false翻折,点false落在点false处,false交false于点false,则false______.
16.在平面直角坐标系中,平行四边形false的边false落在false轴的正半轴上,且点false,直线false以每秒2个单位的速度向下平移,经过______秒该直线可将平行四边形false的面积平分.
17.如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中:①△ABD≌△BCF;②四边形BDEF是平行四边形;③S四边形BDEF=false;④S△AEF=false.其中正确的有_____.
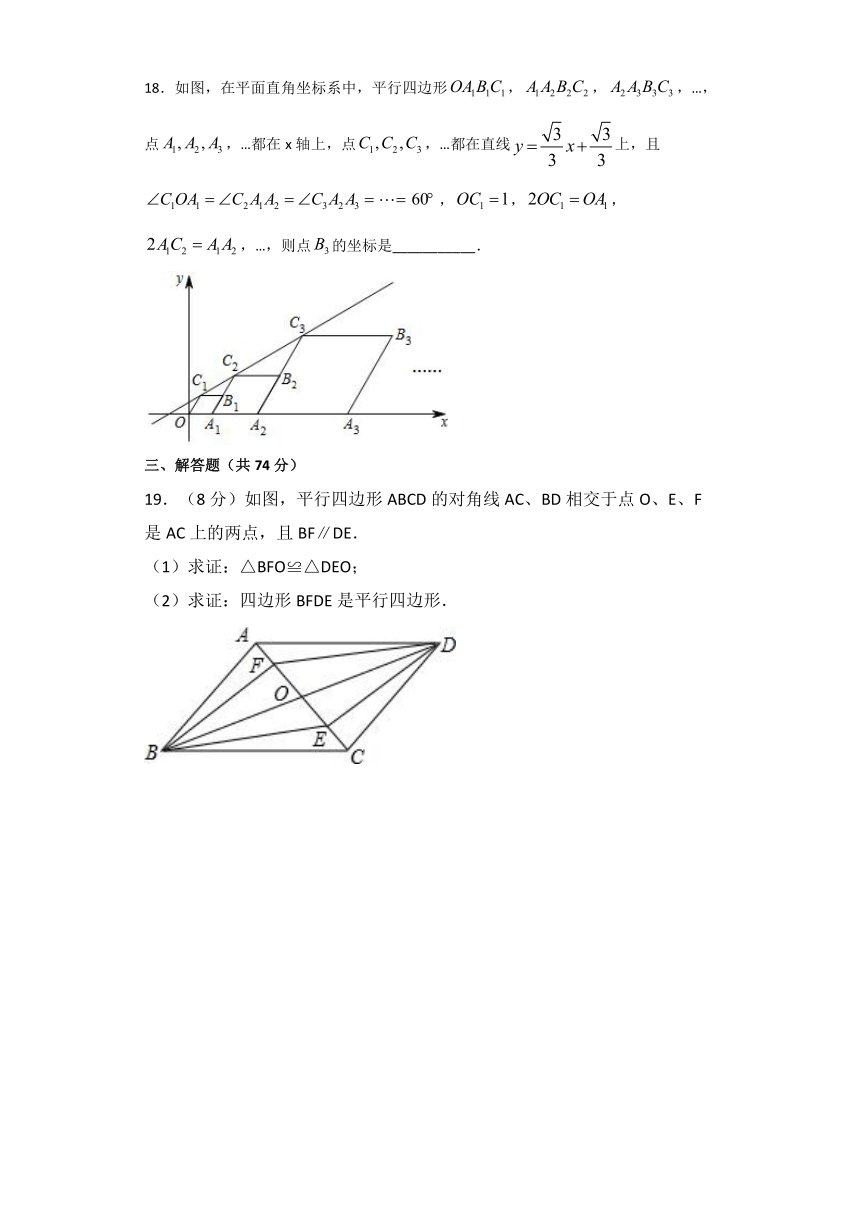
18.如图,在平面直角坐标系中,平行四边形false,false,false,…,点false,…都在x轴上,点false,…都在直线false上,且false,false,false,false,…,则点false的坐标是___________.
三、解答题(共74分)
19.(8分)如图,平行四边形ABCD的对角线AC、BD相交于点O、E、F是AC上的两点,且BF∥DE.
(1)求证:△BFO≌△DEO;
(2)求证:四边形BFDE是平行四边形.
20.(6分)如图,正方形网格中,false均为格点,小正方形的边长为1.请利用正方形网格及无刻度直尺分别画出符合条件的图形.
(1)以false为中心对称点,画一个平行四边形false.
(2)画平行四边形false,使点false到平行四边形false一组邻边的距离相等.
(3)过点false画false的平行线false,并求两平行线之间的距离.
21.(8分)如图,在平行四边形false中,连接false,且false,过点 false作false于点,过点false作false于点 false,且直线false与false之间的距离为false,在false的延长线上取一点 false满足false,求 false的长度.
22.(10分)如图,在false中,false是false边上的高线,false是false边上的中线,false于false.
(1)求证:false.
(2)已知false,求点false到线段false的距离.
(3)在(2)的基础上,求线段false的长度.
23.(10分)点E、F分别在菱形false的边false、false上,false,作false,交false的延长线于点G,连接false、false.
(1)如图1,求证:四边形false是菱形;
(2)如图2,当false平分false时,在不添加辅助线及字母的情况下,请直接写出图中所有的等腰三角形(不包括腰长等于false的等腰三角形)
24.(10分)如图,在四边形false中,false,对角线false交于点false平分false,过点false作false交false的延长线于点false,连接false.
(1)求证:false;
(2)求证:四边形false是菱形;
(3)若false,求false的长.
25.(10分)如图,在平面直角坐标系中,直线l:false 与x轴、y轴分别交于点M,N,高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移,在平移过程中,得到△A1B1C1,当点B1与原点重合时,解答下列问题:
(1)求出点A1的坐标,并判断点A1是否在直线l上;
(2)求出边A1C1所在直线的解析式;
(3)在坐标平面内找一点P,使得以P、A1、C1、M为顶点的四边形是平行四边形,请直接写出P点坐标.
26.(12分)△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF,
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为: ;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE,若已知AB=2false,CD=falseBC,请求出GE的长.
八下中心对称图形单元测试参考答案
1.C
2.B
3.C
4.D
5.C
6.C
7.C
8.D
9.C
10.A
11.-3.
12.14
13.24.
14.(3,6),(-1,-2),(7,2)
15.false
16.6
17.①②③
18.(false,false)
19.(1)见解析;(2)见解析
解:(1)证明:∵四边形ABCD是平行四边形,
∴OB=OD,
∵BF∥DE,
∴∠OFB=∠OED,
在△BFO和△DEO中,
false ,
∴△BFO≌△DEO(AAS);
(2)证明:∵△BFO≌△DEO,
∴OE=OF,
又false OB=OD,
∴四边形BFDE是平行四边形.
20.(1)见解析;(2)见解析;(3)画图见解析,false
解:(1)如图,四边形ABMN即为所画;
(2)如图,四边形ABGH即为所画;
(3)如图,CD即为所画;
AB=false,BP=2,
设点P到AB的距离为h,在△ABP中,
false,
∴点P到AB的距离为h=false=false.
21.8.
解:在平行四边形false中,false,
∵false
false
false
false
false
false之间的距离为false
false
false
false(外角)
又false
false
false
false中,false
false
false
false
22.(1)见解析;(2)3;(3)false
解:(1)连接false,
false是false边上的高线,
false是直角三角形,
false是false边上的中线,
false是false的中点,
即false是false斜边false上的中线,
false,
false,
false,
false,
false;
(2)作false于点false,
false,false,
false,
false,false,
false,
false,
false,
false点false到线段false的距离为3;
(3)false在直角false中,false,false,false,
false.
23.(1)证明见解析;(2)△AEG、△AFG、△CEG、△CFG.
(1)证明:∵ABCD为菱形,
∴AB=AD,∠B=∠D,∠BAC=∠DAC,
∵BE=DF,
∴△ABE≌△ADF,
∴AE=AF,∠BAE=∠DAF,
∴∠EAG=∠FAG,
∵FG//AE,
∴∠EAG=∠FGA,
∴∠FAG=∠FGA,
∴FG=AF=AE,
∵FG//AE,
∴四边形 AEGF是平行四边形,
又AE=AF,
∴四边形 AEGF 是菱形;
(2)由(1)及菱形的性质可得△AEG、△AFG是等腰三角形,
∴∠FAC=∠FGA,
由已知∠DAC=2∠FAC,
∴∠DAC=2∠FGA,
又AD=DC,
∴∠DAC=∠DCA,
∵∠DCA=∠FGA+∠CFG,
∴2∠FGA=∠FGA+∠CFG,
∴∠FGA=∠CFG,
∴△CFG是等腰三角形,
同理可得△CEG也是等腰三角形,
∴符合要求的等腰三角形为△AEG、△AFG、△CEG、△CFG.
24.(1)见解析;(2)见解析;(3)2
解:(1)证明:∵AB//DC,
∴∠OAB=∠DCA,
∵AC平分∠BAD,
∴∠OAB=∠DAC,
∴∠DAC=∠DCA;
(2)证明:∵∠DAC=∠DCA,AB=AD,
∴CD=AD=AB,
∵AB∥DC,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴?ABCD是菱形;
(3)解:∵四边形ABCD是菱形,
∴OA=OC,OB=OD,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=2,
∴OB=falseBD=1,
在Rt△AOB中,由勾股定理得:false,
∴OE=OA=2.
25.(1)A1(false,3),在直线上;(2)false;(3)P1(false,3),P2(false,﹣3),P3(﹣false,3).
解:
(1)
如图,过点A1作A1D⊥OM,垂足为D.
∵△A1B1C1是等边三角形,A1D⊥OM,
∴∠B1A1D=30°,
∴在Rt△A1DB1中,false,
∵A1D=3,
∴在Rt△A1DB1中,false,
∴false,false.
∴点A1的坐标为(false, 3).
由直线l的解析式,得
当x=false时,false,
∴点A1在直线l上.
(2) ∵△A1B1C1是等边三角形,false,
∴false.
∴点C1的坐标为(false, 0).
设直线A1C1的解析式为y=kx+b (k≠0).
将点A1 (false, 3),点C1 (false, 0)的坐标分别代入直线A1C1的解析式,得
false,
解之,得
false,
∴直线A1C1的解析式为false.
(3) 点P的坐标为(false, 3),(false, 3)或(false, -3). 求解过程如下.
根据题意,分别对下面三种情况进行讨论.
①若以∠A1C1M为平行四边形的一个内角,则所求平行四边形为平行四边形A1C1MP.
如图①,过点A1作A1E⊥ON,垂足为E.
由直线l的解析式,得
当y=0时,false,
∴x=false.
∴点M的坐标为(false, 0).
∴OM=false.
∵false,
∴false,
∴false.
∵△A1B1C1是等边三角形,
∴∠A1B1C1=60°,
∴∠A1B1E=90°-∠A1B1C1=90°-60°=30°.
∴在Rt△A1EB1中,false,false.
∵A1P∥C1M,A1E⊥ON,
∴点E,A1,P在同一条直线上,
∴false.
∴点P的坐标为(false, 3).
②若以∠A1MC1为平行四边形的一个内角,则所求平行四边形为平行四边形PC1MA1.
∵A1P∥C1M,
∴A1F⊥ON,
∴在Rt△A1FB1中,false,false.
∵false,
∴false.
∴点P的坐标为(false, 3).
③若以∠C1A1M为平行四边形的一个内角,则所求平行四边形为平行四边形A1C1PM.
如图③,过点P作PG⊥OM,垂足为G.
∵△A1B1C1是等边三角形,
∴∠A1C1B1=60°,
∴∠A1C1M=180°-∠A1C1B1=180°-60°=120°,
∵A1C1∥PM,
∴∠PMC1=∠A1C1M=120°,
∴∠PMG=180°-∠PMC1=180°-120°=60°,
∴在Rt△PMG中,∠MPG=90°-∠PMG=90°-60°=30°.
∵false,
∴在Rt△PGM中,false,
false.
∵OM=false,
∴false.
∴点P的坐标为(false, -3).
综上所述,点P的坐标为(false, 3),(false, 3)或(false, -3).
26.(1)CF⊥BD,BC=CF+CD;(2)成立,证明详见解析;(3).
解:(1)①正方形ADEF中,AD=AF,
∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF,
在△DAB与△FAC中,,
∴△DAB≌△FAC,
∴∠B=∠ACF,
∴∠ACB+∠ACF=90°,即CF⊥BD;
②△DAB≌△FAC,
∴CF=BD,
∵BC=BD+CD,
∴BC=CF+CD;
(2)成立,
∵正方形ADEF中,AD=AF,
∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF,
在△DAB与△FAC中,,
∴△DAB≌△FAC,
∴∠B=∠ACF,CF=BD
∴∠ACB+∠ACF=90°,即CF⊥BD;
∵BC=BD+CD,
∴BC=CF+CD;
(3)解:过A作AH⊥BC于H,过E作EM⊥BD于M,EN⊥CF于N,
∵∠BAC=90°,AB=AC,
∴BC=AB=4,AH=BC=2,
∴CD=BC=1,CH=BC=2,
∴DH=3,
由(2)证得BC⊥CF,CF=BD=5,
∵四边形ADEF是正方形,
∴AD=DE,∠ADE=90°,
∵BC⊥CF,EM⊥BD,EN⊥CF,
∴四边形CMEN是矩形,
∴NE=CM,EM=CN,
∵∠AHD=∠ADC=∠EMD=90°,
∴∠ADH+∠EDM=∠EDM+∠DEM=90°,
∴∠ADH=∠DEM,
在△ADH与△DEM中,,
∴△ADH≌△DEM,
∴EM=DH=3,DM=AH=2,
∴CN=EM=3,EN=CM=3,
∵∠ABC=45°,
∴∠BGC=45°,
∴△BCG是等腰直角三角形,
∴CG=BC=4,
∴GN=1,
∴EG==.
一、单选题(1-10题,每题3分,共30分)
1.下列图案中既是中心对称图形,又是轴对称图形的是( )
A. B. C. D.
2.在四边形false中,给出下列条件:①false;②false;③false;④false.从以上选择两个条件使四边形false为平行四边形的选法有( )
A.3种 B.4种 C.5种 D.6种
3.如图:在平行四边形ABCD中,AB=5,AD=10,BF=3,过BC的中点E作EF⊥AB,垂足为点F.连接DF,求DF的长( )
A.10 B.9 C.8false D.7false
4.如图,在等边△ABC中,BC=8cm,射线AGfalseBC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以3cm/s的速度运动.设运动时间为t(s),当t=( )s时,以A、C、E、F为顶点的四边形是平行四边形.
A.1或2 B.2 C.2或3 D.2或4
5.如图,点E是△ABC内一点,∠AEB=90°,AE平分∠BAC,D是边AB的中点,延长线段DE交边BC于点F,若AB=6,EF=1,则线段AC的长为( )
A.7 B.false C.8 D.9
6.如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F.将△DEF沿EF折叠,点D恰好落在BE上的M点处,延长BC,EF交于点N,下列四个结论不正确的是( )
A.DF=CF B.BF⊥EN
C.△BEN是等边三角形 D.S△BEF=3S△DEF
7.如图,在四边形false中,E,F分别为false、false的中点,G是false的中点,则false与false的关系是( )
A.false B.false C.false D.不确定
8.如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
A.2 B.2false C.3 D.4
9.如图,在四边形ABCD中,AC=BD=6,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2的值为( )
A.9 B.18 C.36 D.48
10.如图,在false中,false,点false分别是边false上的动点,连接false,点false分别为false的中点,连接false,则false的最小值为( ).
A.false B.false C.false D.1
二、填空题(11-18题,每题2分,共16分)
11.若点false和false关于原点对称,则false的值是___________.
12.如图,平行四边形false中,false、false相交于点false,若false,则false的周长为________.
13.如图,平行四边形false的对角线相较于点false,且false,过false作false,交false于点false,若平行四边形false的周长为false,则false的周长为______false.
14.在平面直角坐标系中,已知平行四边形的三个顶点坐标分别是false,则平行四边形第四个顶点D的坐标为__________.
15.已知平行四边形false中,点false和点false分别是边false和false上的点,false,false,将false沿false翻折,点false落在点false处,false交false于点false,则false______.
16.在平面直角坐标系中,平行四边形false的边false落在false轴的正半轴上,且点false,直线false以每秒2个单位的速度向下平移,经过______秒该直线可将平行四边形false的面积平分.
17.如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中:①△ABD≌△BCF;②四边形BDEF是平行四边形;③S四边形BDEF=false;④S△AEF=false.其中正确的有_____.
18.如图,在平面直角坐标系中,平行四边形false,false,false,…,点false,…都在x轴上,点false,…都在直线false上,且false,false,false,false,…,则点false的坐标是___________.
三、解答题(共74分)
19.(8分)如图,平行四边形ABCD的对角线AC、BD相交于点O、E、F是AC上的两点,且BF∥DE.
(1)求证:△BFO≌△DEO;
(2)求证:四边形BFDE是平行四边形.
20.(6分)如图,正方形网格中,false均为格点,小正方形的边长为1.请利用正方形网格及无刻度直尺分别画出符合条件的图形.
(1)以false为中心对称点,画一个平行四边形false.
(2)画平行四边形false,使点false到平行四边形false一组邻边的距离相等.
(3)过点false画false的平行线false,并求两平行线之间的距离.
21.(8分)如图,在平行四边形false中,连接false,且false,过点 false作false于点,过点false作false于点 false,且直线false与false之间的距离为false,在false的延长线上取一点 false满足false,求 false的长度.
22.(10分)如图,在false中,false是false边上的高线,false是false边上的中线,false于false.
(1)求证:false.
(2)已知false,求点false到线段false的距离.
(3)在(2)的基础上,求线段false的长度.
23.(10分)点E、F分别在菱形false的边false、false上,false,作false,交false的延长线于点G,连接false、false.
(1)如图1,求证:四边形false是菱形;
(2)如图2,当false平分false时,在不添加辅助线及字母的情况下,请直接写出图中所有的等腰三角形(不包括腰长等于false的等腰三角形)
24.(10分)如图,在四边形false中,false,对角线false交于点false平分false,过点false作false交false的延长线于点false,连接false.
(1)求证:false;
(2)求证:四边形false是菱形;
(3)若false,求false的长.
25.(10分)如图,在平面直角坐标系中,直线l:false 与x轴、y轴分别交于点M,N,高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移,在平移过程中,得到△A1B1C1,当点B1与原点重合时,解答下列问题:
(1)求出点A1的坐标,并判断点A1是否在直线l上;
(2)求出边A1C1所在直线的解析式;
(3)在坐标平面内找一点P,使得以P、A1、C1、M为顶点的四边形是平行四边形,请直接写出P点坐标.
26.(12分)△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF,
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为: ;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE,若已知AB=2false,CD=falseBC,请求出GE的长.
八下中心对称图形单元测试参考答案
1.C
2.B
3.C
4.D
5.C
6.C
7.C
8.D
9.C
10.A
11.-3.
12.14
13.24.
14.(3,6),(-1,-2),(7,2)
15.false
16.6
17.①②③
18.(false,false)
19.(1)见解析;(2)见解析
解:(1)证明:∵四边形ABCD是平行四边形,
∴OB=OD,
∵BF∥DE,
∴∠OFB=∠OED,
在△BFO和△DEO中,
false ,
∴△BFO≌△DEO(AAS);
(2)证明:∵△BFO≌△DEO,
∴OE=OF,
又false OB=OD,
∴四边形BFDE是平行四边形.
20.(1)见解析;(2)见解析;(3)画图见解析,false
解:(1)如图,四边形ABMN即为所画;
(2)如图,四边形ABGH即为所画;
(3)如图,CD即为所画;
AB=false,BP=2,
设点P到AB的距离为h,在△ABP中,
false,
∴点P到AB的距离为h=false=false.
21.8.
解:在平行四边形false中,false,
∵false
false
false
false
false
false之间的距离为false
false
false
false(外角)
又false
false
false
false中,false
false
false
false
22.(1)见解析;(2)3;(3)false
解:(1)连接false,
false是false边上的高线,
false是直角三角形,
false是false边上的中线,
false是false的中点,
即false是false斜边false上的中线,
false,
false,
false,
false,
false;
(2)作false于点false,
false,false,
false,
false,false,
false,
false,
false,
false点false到线段false的距离为3;
(3)false在直角false中,false,false,false,
false.
23.(1)证明见解析;(2)△AEG、△AFG、△CEG、△CFG.
(1)证明:∵ABCD为菱形,
∴AB=AD,∠B=∠D,∠BAC=∠DAC,
∵BE=DF,
∴△ABE≌△ADF,
∴AE=AF,∠BAE=∠DAF,
∴∠EAG=∠FAG,
∵FG//AE,
∴∠EAG=∠FGA,
∴∠FAG=∠FGA,
∴FG=AF=AE,
∵FG//AE,
∴四边形 AEGF是平行四边形,
又AE=AF,
∴四边形 AEGF 是菱形;
(2)由(1)及菱形的性质可得△AEG、△AFG是等腰三角形,
∴∠FAC=∠FGA,
由已知∠DAC=2∠FAC,
∴∠DAC=2∠FGA,
又AD=DC,
∴∠DAC=∠DCA,
∵∠DCA=∠FGA+∠CFG,
∴2∠FGA=∠FGA+∠CFG,
∴∠FGA=∠CFG,
∴△CFG是等腰三角形,
同理可得△CEG也是等腰三角形,
∴符合要求的等腰三角形为△AEG、△AFG、△CEG、△CFG.
24.(1)见解析;(2)见解析;(3)2
解:(1)证明:∵AB//DC,
∴∠OAB=∠DCA,
∵AC平分∠BAD,
∴∠OAB=∠DAC,
∴∠DAC=∠DCA;
(2)证明:∵∠DAC=∠DCA,AB=AD,
∴CD=AD=AB,
∵AB∥DC,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴?ABCD是菱形;
(3)解:∵四边形ABCD是菱形,
∴OA=OC,OB=OD,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=2,
∴OB=falseBD=1,
在Rt△AOB中,由勾股定理得:false,
∴OE=OA=2.
25.(1)A1(false,3),在直线上;(2)false;(3)P1(false,3),P2(false,﹣3),P3(﹣false,3).
解:
(1)
如图,过点A1作A1D⊥OM,垂足为D.
∵△A1B1C1是等边三角形,A1D⊥OM,
∴∠B1A1D=30°,
∴在Rt△A1DB1中,false,
∵A1D=3,
∴在Rt△A1DB1中,false,
∴false,false.
∴点A1的坐标为(false, 3).
由直线l的解析式,得
当x=false时,false,
∴点A1在直线l上.
(2) ∵△A1B1C1是等边三角形,false,
∴false.
∴点C1的坐标为(false, 0).
设直线A1C1的解析式为y=kx+b (k≠0).
将点A1 (false, 3),点C1 (false, 0)的坐标分别代入直线A1C1的解析式,得
false,
解之,得
false,
∴直线A1C1的解析式为false.
(3) 点P的坐标为(false, 3),(false, 3)或(false, -3). 求解过程如下.
根据题意,分别对下面三种情况进行讨论.
①若以∠A1C1M为平行四边形的一个内角,则所求平行四边形为平行四边形A1C1MP.
如图①,过点A1作A1E⊥ON,垂足为E.
由直线l的解析式,得
当y=0时,false,
∴x=false.
∴点M的坐标为(false, 0).
∴OM=false.
∵false,
∴false,
∴false.
∵△A1B1C1是等边三角形,
∴∠A1B1C1=60°,
∴∠A1B1E=90°-∠A1B1C1=90°-60°=30°.
∴在Rt△A1EB1中,false,false.
∵A1P∥C1M,A1E⊥ON,
∴点E,A1,P在同一条直线上,
∴false.
∴点P的坐标为(false, 3).
②若以∠A1MC1为平行四边形的一个内角,则所求平行四边形为平行四边形PC1MA1.
∵A1P∥C1M,
∴A1F⊥ON,
∴在Rt△A1FB1中,false,false.
∵false,
∴false.
∴点P的坐标为(false, 3).
③若以∠C1A1M为平行四边形的一个内角,则所求平行四边形为平行四边形A1C1PM.
如图③,过点P作PG⊥OM,垂足为G.
∵△A1B1C1是等边三角形,
∴∠A1C1B1=60°,
∴∠A1C1M=180°-∠A1C1B1=180°-60°=120°,
∵A1C1∥PM,
∴∠PMC1=∠A1C1M=120°,
∴∠PMG=180°-∠PMC1=180°-120°=60°,
∴在Rt△PMG中,∠MPG=90°-∠PMG=90°-60°=30°.
∵false,
∴在Rt△PGM中,false,
false.
∵OM=false,
∴false.
∴点P的坐标为(false, -3).
综上所述,点P的坐标为(false, 3),(false, 3)或(false, -3).
26.(1)CF⊥BD,BC=CF+CD;(2)成立,证明详见解析;(3).
解:(1)①正方形ADEF中,AD=AF,
∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF,
在△DAB与△FAC中,,
∴△DAB≌△FAC,
∴∠B=∠ACF,
∴∠ACB+∠ACF=90°,即CF⊥BD;
②△DAB≌△FAC,
∴CF=BD,
∵BC=BD+CD,
∴BC=CF+CD;
(2)成立,
∵正方形ADEF中,AD=AF,
∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF,
在△DAB与△FAC中,,
∴△DAB≌△FAC,
∴∠B=∠ACF,CF=BD
∴∠ACB+∠ACF=90°,即CF⊥BD;
∵BC=BD+CD,
∴BC=CF+CD;
(3)解:过A作AH⊥BC于H,过E作EM⊥BD于M,EN⊥CF于N,
∵∠BAC=90°,AB=AC,
∴BC=AB=4,AH=BC=2,
∴CD=BC=1,CH=BC=2,
∴DH=3,
由(2)证得BC⊥CF,CF=BD=5,
∵四边形ADEF是正方形,
∴AD=DE,∠ADE=90°,
∵BC⊥CF,EM⊥BD,EN⊥CF,
∴四边形CMEN是矩形,
∴NE=CM,EM=CN,
∵∠AHD=∠ADC=∠EMD=90°,
∴∠ADH+∠EDM=∠EDM+∠DEM=90°,
∴∠ADH=∠DEM,
在△ADH与△DEM中,,
∴△ADH≌△DEM,
∴EM=DH=3,DM=AH=2,
∴CN=EM=3,EN=CM=3,
∵∠ABC=45°,
∴∠BGC=45°,
∴△BCG是等腰直角三角形,
∴CG=BC=4,
∴GN=1,
∴EG==.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
