8.3理想气体的状态方程 同步一节一练(word版含答案)
文档属性
| 名称 | 8.3理想气体的状态方程 同步一节一练(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 403.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-06-01 00:00:00 | ||
图片预览

文档简介
8.3理想气体的状态方程
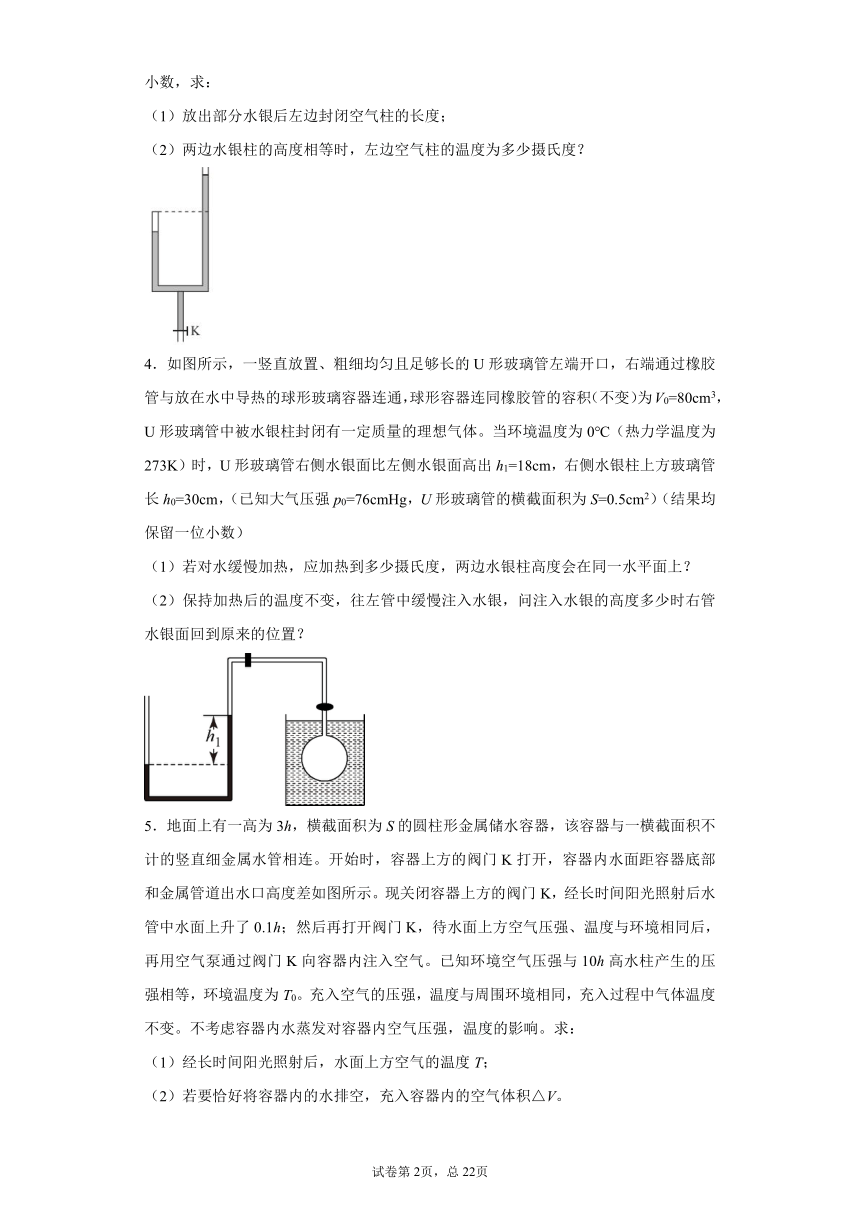
1.如图所示,一导热性良好的汽缸内用活塞封住一定量的气体(不计活塞与缸壁摩擦),温度升高时,下列物理量发生变化的是( )
A.活塞高度h B.汽缸高度H
C.气体压强p D.弹簧长度L
2.某同学设计了如图所示测量液体密度的装置:左侧为上端开口的圆柱形玻璃缸右侧为上端封闭、高为L0=52cm的玻璃管,两容器底部用细管相连,且左侧玻璃缸横截面积远远大于右侧玻璃管横截面积,两容器导热性能良好。环境温度T=300K。现向左侧玻璃缸缓慢注入待测液体,将原长为L0的空气柱封闭在玻璃管中,当左侧液面高度h1=52cm时,右管内液柱高度h2=2cm。已知大气压强p0=1.0×105Pa,重力加速度g取10m/s2
①求待测液体的密度;
②将右侧玻璃管内气体温度缓慢升高,当右管内液体刚好全部挤出时,求管内空气的温度。(计算结果保留三位有效数字)
3.如图所示,一粗细均匀的U形细玻璃管竖直放置并盛有水银,左端封闭一定质量、长度为L=5.0cm的空气,右端足够长且上端开口与大气相通。玻璃管底部有一处于关闭状态的绝热开关K,此时右侧管中的水银面比左侧管中的水银面高h1=16.0cm,现将开关K打开,从玻璃管中缓慢放出部分水银,当左侧水银面比右侧水银面高h2=10.0cm时,将开关K关闭,此时玻璃管内左边空气柱的温度为27℃,并对左侧玻璃管内的空气加热至两边水银柱等高。已知大气压强p0=75.0cmHg。取T=t+273℃,计算结果保留一位小数,求:
(1)放出部分水银后左边封闭空气柱的长度;
(2)两边水银柱的高度相等时,左边空气柱的温度为多少摄氏度?
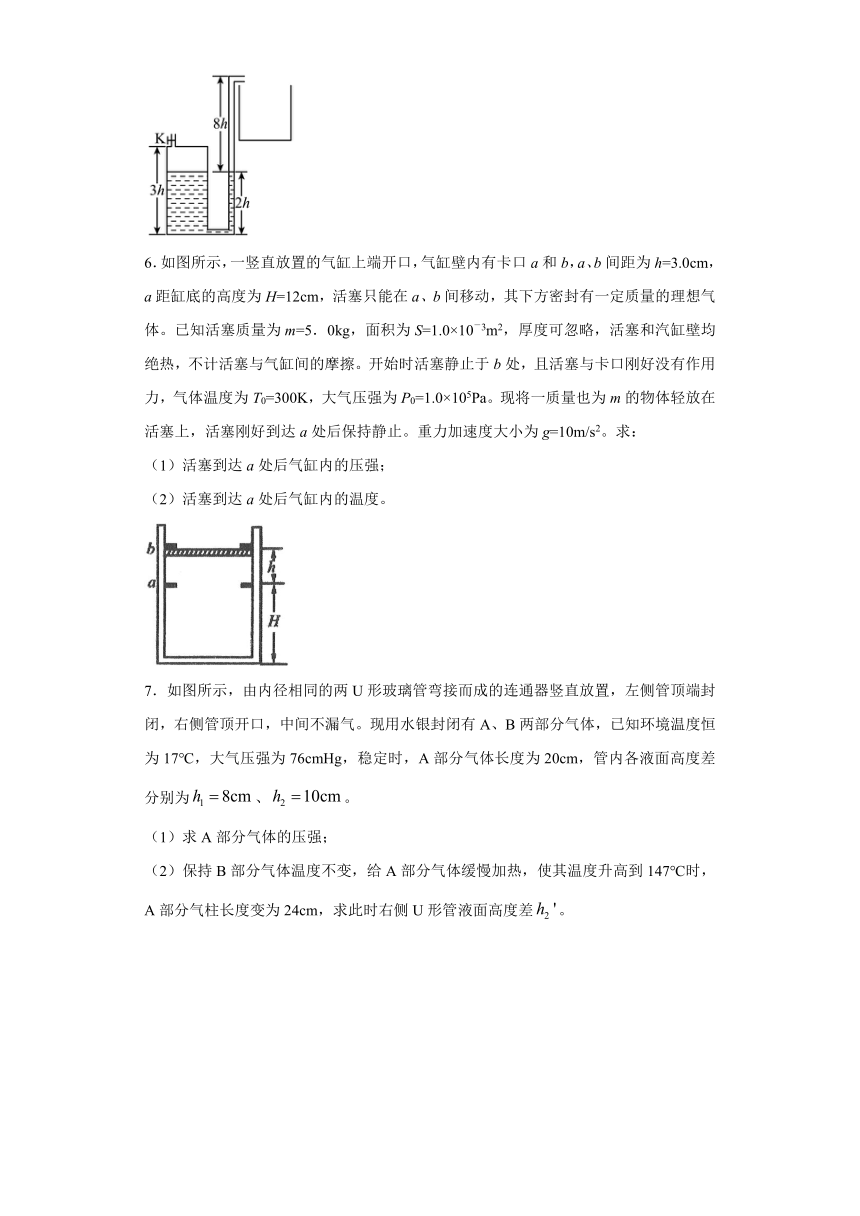
4.如图所示,一竖直放置、粗细均匀且足够长的U形玻璃管左端开口,右端通过橡胶管与放在水中导热的球形玻璃容器连通,球形容器连同橡胶管的容积(不变)为V0=80cm3,U形玻璃管中被水银柱封闭有一定质量的理想气体。当环境温度为0℃(热力学温度为273K)时,U形玻璃管右侧水银面比左侧水银面高出h1=18cm,右侧水银柱上方玻璃管长h0=30cm,(已知大气压强p0=76cmHg,U形玻璃管的横截面积为S=0.5cm2)(结果均保留一位小数)
(1)若对水缓慢加热,应加热到多少摄氏度,两边水银柱高度会在同一水平面上?
(2)保持加热后的温度不变,往左管中缓慢注入水银,问注入水银的高度多少时右管水银面回到原来的位置?
5.地面上有一高为3h,横截面积为S的圆柱形金属储水容器,该容器与一横截面积不计的竖直细金属水管相连。开始时,容器上方的阀门K打开,容器内水面距容器底部和金属管道出水口高度差如图所示。现关闭容器上方的阀门K,经长时间阳光照射后水管中水面上升了0.1h;然后再打开阀门K,待水面上方空气压强、温度与环境相同后,再用空气泵通过阀门K向容器内注入空气。已知环境空气压强与10h高水柱产生的压强相等,环境温度为T0。充入空气的压强,温度与周围环境相同,充入过程中气体温度不变。不考虑容器内水蒸发对容器内空气压强,温度的影响。求:
(1)经长时间阳光照射后,水面上方空气的温度T;
(2)若要恰好将容器内的水排空,充入容器内的空气体积△V。
6.如图所示,一竖直放置的气缸上端开口,气缸壁内有卡口a和b,a、b间距为h=3.0cm,a距缸底的高度为H=12cm,活塞只能在a、b间移动,其下方密封有一定质量的理想气体。已知活塞质量为m=5.0kg,面积为S=1.0×10-3m2,厚度可忽略,活塞和汽缸壁均绝热,不计活塞与气缸间的摩擦。开始时活塞静止于b处,且活塞与卡口刚好没有作用力,气体温度为T0=300K,大气压强为P0=1.0×105Pa。现将一质量也为m的物体轻放在活塞上,活塞刚好到达a处后保持静止。重力加速度大小为g=10m/s2。求:
(1)活塞到达a处后气缸内的压强;
(2)活塞到达a处后气缸内的温度。
7.如图所示,由内径相同的两U形玻璃管弯接而成的连通器竖直放置,左侧管顶端封闭,右侧管顶开口,中间不漏气。现用水银封闭有A、B两部分气体,已知环境温度恒为17℃,大气压强为76cmHg,稳定时,A部分气体长度为20cm,管内各液面高度差分别为false、false。
(1)求A部分气体的压强;
(2)保持B部分气体温度不变,给A部分气体缓慢加热,使其温度升高到147℃时,A部分气柱长度变为24cm,求此时右侧U形管液面高度差false。
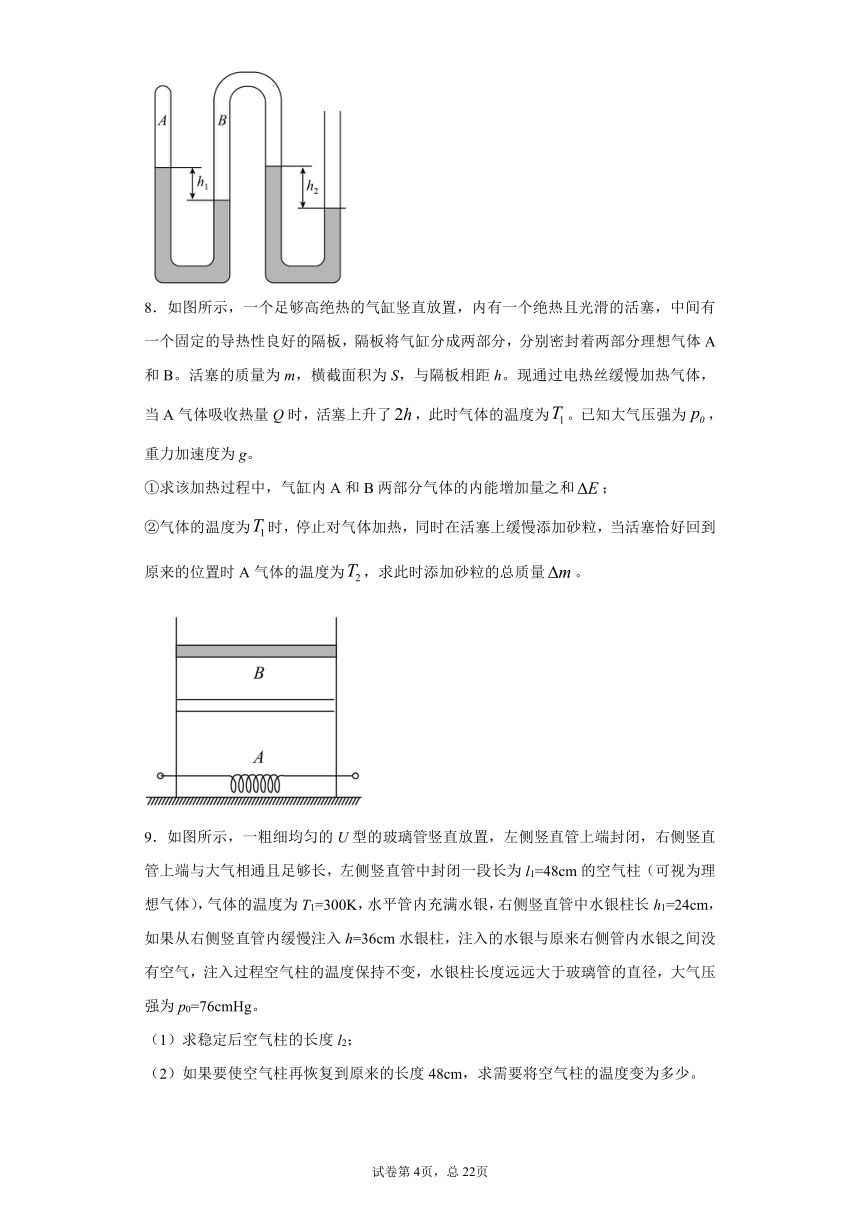
8.如图所示,一个足够高绝热的气缸竖直放置,内有一个绝热且光滑的活塞,中间有一个固定的导热性良好的隔板,隔板将气缸分成两部分,分别密封着两部分理想气体A和B。活塞的质量为m,横截面积为S,与隔板相距h。现通过电热丝缓慢加热气体,当A气体吸收热量Q时,活塞上升了false,此时气体的温度为false。已知大气压强为false,重力加速度为g。
①求该加热过程中,气缸内A和B两部分气体的内能增加量之和false;
②气体的温度为false时,停止对气体加热,同时在活塞上缓慢添加砂粒,当活塞恰好回到原来的位置时A气体的温度为false,求此时添加砂粒的总质量false。
9.如图所示,一粗细均匀的U型的玻璃管竖直放置,左侧竖直管上端封闭,右侧竖直管上端与大气相通且足够长,左侧竖直管中封闭一段长为l1=48cm的空气柱(可视为理想气体),气体的温度为T1=300K,水平管内充满水银,右侧竖直管中水银柱长h1=24cm,如果从右侧竖直管内缓慢注入h=36cm水银柱,注入的水银与原来右侧管内水银之间没有空气,注入过程空气柱的温度保持不变,水银柱长度远远大于玻璃管的直径,大气压强为p0=76cmHg。
(1)求稳定后空气柱的长度l2;
(2)如果要使空气柱再恢复到原来的长度48cm,求需要将空气柱的温度变为多少。
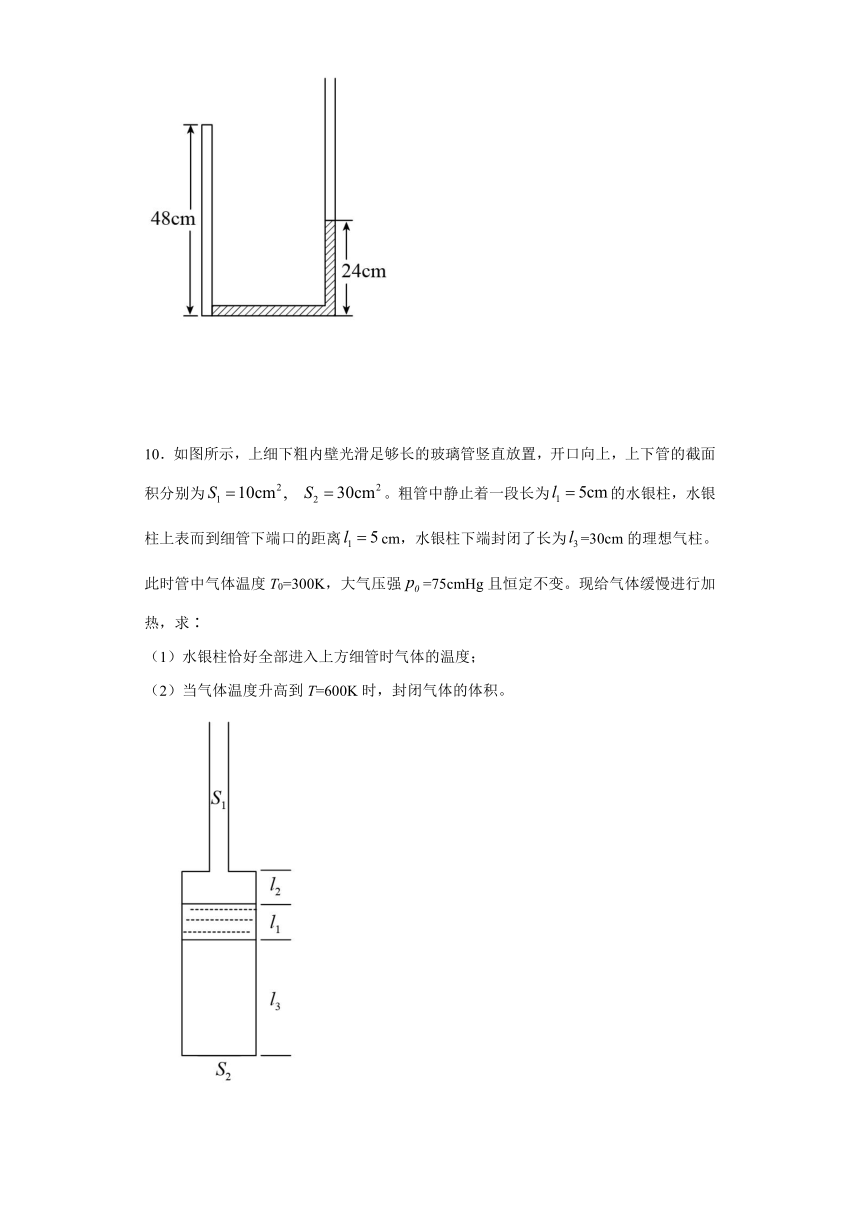
10.如图所示,上细下粗内壁光滑足够长的玻璃管竖直放置,开口向上,上下管的截面积分别为false。粗管中静止着一段长为false的水银柱,水银柱上表而到细管下端口的距离falsecm,水银柱下端封闭了长为false=30cm的理想气柱。此时管中气体温度T0=300K,大气压强false=75cmHg且恒定不变。现给气体缓慢进行加热,求∶
(1)水银柱恰好全部进入上方细管时气体的温度;
(2)当气体温度升高到T=600K时,封闭气体的体积。
11.肺活量是常用来衡量人体心肺功能的重要指标。肺活量是指在标准大气压false下人一次尽力吸气后,再尽力呼出的气体体积总量。某同学在学习气体实验定律后,设计了一个吹气球实验来粗测自己肺活量。该同学先尽最大努力吸气,然后通过气球口尽力向气球内吹气,气球没有被吹爆,此时气球可近似看成球形,过一段时间稳定后测得气球的直径falsecm。已知气球橡胶薄膜产生的附加压强false,其中false为薄膜的等效表面张力系数,R为气球充气后的半径。如图为该气球的等效表面张力系数false随气球半径R的变化曲线。吹气前气球内部的空气可忽略不计,空气可看作理想气体,人的体温为37℃,环境温度为27℃,大气压强false,false。求:
(1)吹气后稳定时气球内气体的压强;
(2)该同学的肺活量为多少毫升。
12.导热良好、粗细均匀的U形玻璃管竖直放置,左端封闭,右端开口初始时,管内水银柱及空气柱长度如图所示,下方水银柱足够长且左、右两侧水银面等高。已知大气压强false保持不变,环境初始温度为false。现缓慢将玻璃管处环境温度提升至false。求:
(1)右侧空气柱长度;
(2)左侧管内水银面下降的高度。
13.如图所示,上端开口的内壁光滑圆柱形汽缸固定在倾角为30°的斜面上,一上端固定的轻弹簧与横截面积为40cm2的活塞相连接,汽缸内封闭一定质量的理想气体。在汽缸内距缸底60cm处有卡环,活塞只能向上滑动。开始时活塞搁在卡环上,且弹簧处于原长,缸内气体的压强等于大气压强p0=1.0×105Pa,温度为300 K。现对汽缸内的气体缓慢加热,当温度增加30K时,活塞恰好离开卡环,当温度增加到480K时,活塞移动了20cm。已知g=10m/s2,求:
(1)活塞的质量;
(2)弹簧的劲度系数k。
8.3理想气体的状态方程
1.如图所示,一导热性良好的汽缸内用活塞封住一定量的气体(不计活塞与缸壁摩擦),温度升高时,下列物理量发生变化的是( )
A.活塞高度h B.汽缸高度H
C.气体压强p D.弹簧长度L
【答案】B
【解析】AD.根据整体法分析可知,弹簧的拉力大小等于活塞、汽缸以及气体重力之和,所以当温度升高时,弹簧拉力大小不变,根据胡克定律可知弹簧伸长量不变,即弹簧长度L不变,根据长度关系分析可知,活塞高度h也不变,故AD不符合题意;
C.对活塞单独进行受力分析,由题意及上述分析可知活塞受力情况不变,则气体压强p不变,故C不符合题意;
B.根据理想气体状态方程false=C可知,当T增大且p不变时,气体体积V增大,所以汽缸将向下运动,则汽缸高度H减小,故B符合题意。
故选B。
2.某同学设计了如图所示测量液体密度的装置:左侧为上端开口的圆柱形玻璃缸右侧为上端封闭、高为L0=52cm的玻璃管,两容器底部用细管相连,且左侧玻璃缸横截面积远远大于右侧玻璃管横截面积,两容器导热性能良好。环境温度T=300K。现向左侧玻璃缸缓慢注入待测液体,将原长为L0的空气柱封闭在玻璃管中,当左侧液面高度h1=52cm时,右管内液柱高度h2=2cm。已知大气压强p0=1.0×105Pa,重力加速度g取10m/s2
①求待测液体的密度;
②将右侧玻璃管内气体温度缓慢升高,当右管内液体刚好全部挤出时,求管内空气的温度。(计算结果保留三位有效数字)
【答案】(1)8×102kg/m3;(2)312K
【解析】①设右管横截面积为S,对右管内的气体,由玻意耳定律
p0V0=p1V1
其中
V0=L0S
V1=(L0-h2)S
解得
p1=1.04×105Pa
又
p1=p0+ρg(h1-h2)
解得
ρ=8×102kg/m3
②对右管内的气体,根据理想气体状态方程
false
其中
p2=p0+ρgh1
解得
T′=312K
3.如图所示,一粗细均匀的U形细玻璃管竖直放置并盛有水银,左端封闭一定质量、长度为L=5.0cm的空气,右端足够长且上端开口与大气相通。玻璃管底部有一处于关闭状态的绝热开关K,此时右侧管中的水银面比左侧管中的水银面高h1=16.0cm,现将开关K打开,从玻璃管中缓慢放出部分水银,当左侧水银面比右侧水银面高h2=10.0cm时,将开关K关闭,此时玻璃管内左边空气柱的温度为27℃,并对左侧玻璃管内的空气加热至两边水银柱等高。已知大气压强p0=75.0cmHg。取T=t+273℃,计算结果保留一位小数,求:
(1)放出部分水银后左边封闭空气柱的长度;
(2)两边水银柱的高度相等时,左边空气柱的温度为多少摄氏度?
【答案】(1)7.0cm;(2)320.4℃
【解析】(1)设玻璃管的横截面积为S,放出部分水银后封闭空气柱的长度为L1,压强为p,由玻意耳定律可知
false
由平衡条件可知
false
打开开关K放出部分水银后
false
联立解得
L1=7.0cm
(2)由加热后左右两边水银柱相平可知,左边封闭空气柱的压强
false
加热后左边空气柱的长度
false
根据理想气体状态变化方程可知
false
即
false
解得
false
即
false
4.如图所示,一竖直放置、粗细均匀且足够长的U形玻璃管左端开口,右端通过橡胶管与放在水中导热的球形玻璃容器连通,球形容器连同橡胶管的容积(不变)为V0=80cm3,U形玻璃管中被水银柱封闭有一定质量的理想气体。当环境温度为0℃(热力学温度为273K)时,U形玻璃管右侧水银面比左侧水银面高出h1=18cm,右侧水银柱上方玻璃管长h0=30cm,(已知大气压强p0=76cmHg,U形玻璃管的横截面积为S=0.5cm2)(结果均保留一位小数)
(1)若对水缓慢加热,应加热到多少摄氏度,两边水银柱高度会在同一水平面上?
(2)保持加热后的温度不变,往左管中缓慢注入水银,问注入水银的高度多少时右管水银面回到原来的位置?
【答案】(1)t=118.6℃;(2)25.2cm
【解析】(1)对封闭的气体分析,初状态有
p1=p0-18cmHg=58cmHg
V1=V0+h0S
T1=273K
末状态有
p2=p0
V2=V1+falseS
T2=(273+t)K
由理想气体状态方程有
false
代入数据得
t=118.6℃
(2)当往左管注入水银后,末状态压强为p,体积为
V1=V0+h0S
由玻意耳定律有
p2V2=pV1
解得
p=83.2cmHg
可知往左管注入水银的高度为
h=h1+△h=25.2cm
5.地面上有一高为3h,横截面积为S的圆柱形金属储水容器,该容器与一横截面积不计的竖直细金属水管相连。开始时,容器上方的阀门K打开,容器内水面距容器底部和金属管道出水口高度差如图所示。现关闭容器上方的阀门K,经长时间阳光照射后水管中水面上升了0.1h;然后再打开阀门K,待水面上方空气压强、温度与环境相同后,再用空气泵通过阀门K向容器内注入空气。已知环境空气压强与10h高水柱产生的压强相等,环境温度为T0。充入空气的压强,温度与周围环境相同,充入过程中气体温度不变。不考虑容器内水蒸发对容器内空气压强,温度的影响。求:
(1)经长时间阳光照射后,水面上方空气的温度T;
(2)若要恰好将容器内的水排空,充入容器内的空气体积△V。
【答案】(1)1.01false;(2)false
【解析】(1)由题可知
false
光照后
false
所以
false
金属管横截面积不计属于等体积变化,由查理定律得
false
解得
false
(2)因为水恰好排空,所以最终气体体积
false
false
由理想气体状态方程可得
false
其中
false
所以
false
6.如图所示,一竖直放置的气缸上端开口,气缸壁内有卡口a和b,a、b间距为h=3.0cm,a距缸底的高度为H=12cm,活塞只能在a、b间移动,其下方密封有一定质量的理想气体。已知活塞质量为m=5.0kg,面积为S=1.0×10-3m2,厚度可忽略,活塞和汽缸壁均绝热,不计活塞与气缸间的摩擦。开始时活塞静止于b处,且活塞与卡口刚好没有作用力,气体温度为T0=300K,大气压强为P0=1.0×105Pa。现将一质量也为m的物体轻放在活塞上,活塞刚好到达a处后保持静止。重力加速度大小为g=10m/s2。求:
(1)活塞到达a处后气缸内的压强;
(2)活塞到达a处后气缸内的温度。
【答案】(1)false(2)false
【解析】(1)活塞恰好静止在a处,由平衡得
false
解得
false
同理可得活塞恰好静止在b处
false
解得
false
(2)由理想气体状态方程
false
解得
false
7.如图所示,由内径相同的两U形玻璃管弯接而成的连通器竖直放置,左侧管顶端封闭,右侧管顶开口,中间不漏气。现用水银封闭有A、B两部分气体,已知环境温度恒为17℃,大气压强为76cmHg,稳定时,A部分气体长度为20cm,管内各液面高度差分别为false、false。
(1)求A部分气体的压强;
(2)保持B部分气体温度不变,给A部分气体缓慢加热,使其温度升高到147℃时,A部分气柱长度变为24cm,求此时右侧U形管液面高度差false。
【答案】(1)false;(2)false
【解析】(1)中间B气体压强
false
A部分气体压强
false
(2)A部分气体加热后,有
false
得
false
由于左边水银高度相等,则中间B气体的压强
false
解得
false
8.如图所示,一个足够高绝热的气缸竖直放置,内有一个绝热且光滑的活塞,中间有一个固定的导热性良好的隔板,隔板将气缸分成两部分,分别密封着两部分理想气体A和B。活塞的质量为m,横截面积为S,与隔板相距h。现通过电热丝缓慢加热气体,当A气体吸收热量Q时,活塞上升了false,此时气体的温度为false。已知大气压强为false,重力加速度为g。
①求该加热过程中,气缸内A和B两部分气体的内能增加量之和false;
②气体的温度为false时,停止对气体加热,同时在活塞上缓慢添加砂粒,当活塞恰好回到原来的位置时A气体的温度为false,求此时添加砂粒的总质量false。
【答案】①false;②false
【解析】①气体B的压强为
false
B气体对外做的功
false
由热力学第一定律得
false
解得
false
②B气体的初状态
压强
false
体积
false
温度false
B气体末状态
压强
false
体积
false
温度false
由理想气体状态方程
false
解得
false
9.如图所示,一粗细均匀的U型的玻璃管竖直放置,左侧竖直管上端封闭,右侧竖直管上端与大气相通且足够长,左侧竖直管中封闭一段长为l1=48cm的空气柱(可视为理想气体),气体的温度为T1=300K,水平管内充满水银,右侧竖直管中水银柱长h1=24cm,如果从右侧竖直管内缓慢注入h=36cm水银柱,注入的水银与原来右侧管内水银之间没有空气,注入过程空气柱的温度保持不变,水银柱长度远远大于玻璃管的直径,大气压强为p0=76cmHg。
(1)求稳定后空气柱的长度l2;
(2)如果要使空气柱再恢复到原来的长度48cm,求需要将空气柱的温度变为多少。
【答案】(1)40cm;(2)408K
【解析】(1)初始状态下气体的压强为
false
空气柱长度
false
设玻璃管横截面积为S,气体的体积为
false
设注入水银后水平管进入左侧竖直管内水银长度为x,则气体的压强为
false
气体的体积为
false
注入过程气体温度不变,根据玻意耳定律得
false
解得
false
则稳定后空气柱的长度
false
(2)要使空气柱变为原来长度则气体压强变为
false
根据查理定律
false
解得空气柱的温度变为
false
10.如图所示,上细下粗内壁光滑足够长的玻璃管竖直放置,开口向上,上下管的截面积分别为false。粗管中静止着一段长为false的水银柱,水银柱上表而到细管下端口的距离falsecm,水银柱下端封闭了长为false=30cm的理想气柱。此时管中气体温度T0=300K,大气压强false=75cmHg且恒定不变。现给气体缓慢进行加热,求∶
(1)水银柱恰好全部进入上方细管时气体的温度;
(2)当气体温度升高到T=600K时,封闭气体的体积。
【答案】(1)450K;(2)1600cm3
【解析】(1)气体初态压强
p1=p0+ρgl1=80cmHg
末态压强
p2=p0+ρgl4
其中
l1S1=l4S2
气体满足
false
联立解得
T1=450K
(2)继续升温,气体压强保持不变,有
false
解得
V=1600cm3
11.肺活量是常用来衡量人体心肺功能的重要指标。肺活量是指在标准大气压false下人一次尽力吸气后,再尽力呼出的气体体积总量。某同学在学习气体实验定律后,设计了一个吹气球实验来粗测自己肺活量。该同学先尽最大努力吸气,然后通过气球口尽力向气球内吹气,气球没有被吹爆,此时气球可近似看成球形,过一段时间稳定后测得气球的直径falsecm。已知气球橡胶薄膜产生的附加压强false,其中false为薄膜的等效表面张力系数,R为气球充气后的半径。如图为该气球的等效表面张力系数false随气球半径R的变化曲线。吹气前气球内部的空气可忽略不计,空气可看作理想气体,人的体温为37℃,环境温度为27℃,大气压强false,false。求:
(1)吹气后稳定时气球内气体的压强;
(2)该同学的肺活量为多少毫升。
【答案】(1)false;(2)false
【解析】(1)由图像可知气球半径
false
则气球橡胶薄膜的等效表面张力系数
false
吹气后稳定时气球内气体的压强
false
解得
false
(2)设该同学的肺活量为false,由理想气体状态方程得
false
false
解得:
false
12.导热良好、粗细均匀的U形玻璃管竖直放置,左端封闭,右端开口初始时,管内水银柱及空气柱长度如图所示,下方水银柱足够长且左、右两侧水银面等高。已知大气压强false保持不变,环境初始温度为false。现缓慢将玻璃管处环境温度提升至false。求:
(1)右侧空气柱长度;
(2)左侧管内水银面下降的高度。
【答案】(1)5.5cm;(2)1.83cm
【解析】(1) 对右侧气体,初态
false?=90cmHg,false,false
末态
false,false,false
根据
false
解得
false
(2)对左侧气体
false?=90cmHg,false,false
末态
false,false,false
根据理想气体状态方程
false
左侧管内水银面下降的高度
false
13.如图所示,上端开口的内壁光滑圆柱形汽缸固定在倾角为30°的斜面上,一上端固定的轻弹簧与横截面积为40cm2的活塞相连接,汽缸内封闭一定质量的理想气体。在汽缸内距缸底60cm处有卡环,活塞只能向上滑动。开始时活塞搁在卡环上,且弹簧处于原长,缸内气体的压强等于大气压强p0=1.0×105Pa,温度为300 K。现对汽缸内的气体缓慢加热,当温度增加30K时,活塞恰好离开卡环,当温度增加到480K时,活塞移动了20cm。已知g=10m/s2,求:
(1)活塞的质量;
(2)弹簧的劲度系数k。
【答案】(1)8kg;(2)200N/m
【解析】(1)气体温度从300K增加到330K的过程中,经历等容变化,则有
false
解得:false;
此时,活塞恰好离开卡环,可得:
false
解得:false;
(2)气体温度从330K增加到480K的过程中,则
false
解得:false;
对活塞受力分析可得
false
解得:false。
1.如图所示,一导热性良好的汽缸内用活塞封住一定量的气体(不计活塞与缸壁摩擦),温度升高时,下列物理量发生变化的是( )
A.活塞高度h B.汽缸高度H
C.气体压强p D.弹簧长度L
2.某同学设计了如图所示测量液体密度的装置:左侧为上端开口的圆柱形玻璃缸右侧为上端封闭、高为L0=52cm的玻璃管,两容器底部用细管相连,且左侧玻璃缸横截面积远远大于右侧玻璃管横截面积,两容器导热性能良好。环境温度T=300K。现向左侧玻璃缸缓慢注入待测液体,将原长为L0的空气柱封闭在玻璃管中,当左侧液面高度h1=52cm时,右管内液柱高度h2=2cm。已知大气压强p0=1.0×105Pa,重力加速度g取10m/s2
①求待测液体的密度;
②将右侧玻璃管内气体温度缓慢升高,当右管内液体刚好全部挤出时,求管内空气的温度。(计算结果保留三位有效数字)
3.如图所示,一粗细均匀的U形细玻璃管竖直放置并盛有水银,左端封闭一定质量、长度为L=5.0cm的空气,右端足够长且上端开口与大气相通。玻璃管底部有一处于关闭状态的绝热开关K,此时右侧管中的水银面比左侧管中的水银面高h1=16.0cm,现将开关K打开,从玻璃管中缓慢放出部分水银,当左侧水银面比右侧水银面高h2=10.0cm时,将开关K关闭,此时玻璃管内左边空气柱的温度为27℃,并对左侧玻璃管内的空气加热至两边水银柱等高。已知大气压强p0=75.0cmHg。取T=t+273℃,计算结果保留一位小数,求:
(1)放出部分水银后左边封闭空气柱的长度;
(2)两边水银柱的高度相等时,左边空气柱的温度为多少摄氏度?
4.如图所示,一竖直放置、粗细均匀且足够长的U形玻璃管左端开口,右端通过橡胶管与放在水中导热的球形玻璃容器连通,球形容器连同橡胶管的容积(不变)为V0=80cm3,U形玻璃管中被水银柱封闭有一定质量的理想气体。当环境温度为0℃(热力学温度为273K)时,U形玻璃管右侧水银面比左侧水银面高出h1=18cm,右侧水银柱上方玻璃管长h0=30cm,(已知大气压强p0=76cmHg,U形玻璃管的横截面积为S=0.5cm2)(结果均保留一位小数)
(1)若对水缓慢加热,应加热到多少摄氏度,两边水银柱高度会在同一水平面上?
(2)保持加热后的温度不变,往左管中缓慢注入水银,问注入水银的高度多少时右管水银面回到原来的位置?
5.地面上有一高为3h,横截面积为S的圆柱形金属储水容器,该容器与一横截面积不计的竖直细金属水管相连。开始时,容器上方的阀门K打开,容器内水面距容器底部和金属管道出水口高度差如图所示。现关闭容器上方的阀门K,经长时间阳光照射后水管中水面上升了0.1h;然后再打开阀门K,待水面上方空气压强、温度与环境相同后,再用空气泵通过阀门K向容器内注入空气。已知环境空气压强与10h高水柱产生的压强相等,环境温度为T0。充入空气的压强,温度与周围环境相同,充入过程中气体温度不变。不考虑容器内水蒸发对容器内空气压强,温度的影响。求:
(1)经长时间阳光照射后,水面上方空气的温度T;
(2)若要恰好将容器内的水排空,充入容器内的空气体积△V。
6.如图所示,一竖直放置的气缸上端开口,气缸壁内有卡口a和b,a、b间距为h=3.0cm,a距缸底的高度为H=12cm,活塞只能在a、b间移动,其下方密封有一定质量的理想气体。已知活塞质量为m=5.0kg,面积为S=1.0×10-3m2,厚度可忽略,活塞和汽缸壁均绝热,不计活塞与气缸间的摩擦。开始时活塞静止于b处,且活塞与卡口刚好没有作用力,气体温度为T0=300K,大气压强为P0=1.0×105Pa。现将一质量也为m的物体轻放在活塞上,活塞刚好到达a处后保持静止。重力加速度大小为g=10m/s2。求:
(1)活塞到达a处后气缸内的压强;
(2)活塞到达a处后气缸内的温度。
7.如图所示,由内径相同的两U形玻璃管弯接而成的连通器竖直放置,左侧管顶端封闭,右侧管顶开口,中间不漏气。现用水银封闭有A、B两部分气体,已知环境温度恒为17℃,大气压强为76cmHg,稳定时,A部分气体长度为20cm,管内各液面高度差分别为false、false。
(1)求A部分气体的压强;
(2)保持B部分气体温度不变,给A部分气体缓慢加热,使其温度升高到147℃时,A部分气柱长度变为24cm,求此时右侧U形管液面高度差false。
8.如图所示,一个足够高绝热的气缸竖直放置,内有一个绝热且光滑的活塞,中间有一个固定的导热性良好的隔板,隔板将气缸分成两部分,分别密封着两部分理想气体A和B。活塞的质量为m,横截面积为S,与隔板相距h。现通过电热丝缓慢加热气体,当A气体吸收热量Q时,活塞上升了false,此时气体的温度为false。已知大气压强为false,重力加速度为g。
①求该加热过程中,气缸内A和B两部分气体的内能增加量之和false;
②气体的温度为false时,停止对气体加热,同时在活塞上缓慢添加砂粒,当活塞恰好回到原来的位置时A气体的温度为false,求此时添加砂粒的总质量false。
9.如图所示,一粗细均匀的U型的玻璃管竖直放置,左侧竖直管上端封闭,右侧竖直管上端与大气相通且足够长,左侧竖直管中封闭一段长为l1=48cm的空气柱(可视为理想气体),气体的温度为T1=300K,水平管内充满水银,右侧竖直管中水银柱长h1=24cm,如果从右侧竖直管内缓慢注入h=36cm水银柱,注入的水银与原来右侧管内水银之间没有空气,注入过程空气柱的温度保持不变,水银柱长度远远大于玻璃管的直径,大气压强为p0=76cmHg。
(1)求稳定后空气柱的长度l2;
(2)如果要使空气柱再恢复到原来的长度48cm,求需要将空气柱的温度变为多少。
10.如图所示,上细下粗内壁光滑足够长的玻璃管竖直放置,开口向上,上下管的截面积分别为false。粗管中静止着一段长为false的水银柱,水银柱上表而到细管下端口的距离falsecm,水银柱下端封闭了长为false=30cm的理想气柱。此时管中气体温度T0=300K,大气压强false=75cmHg且恒定不变。现给气体缓慢进行加热,求∶
(1)水银柱恰好全部进入上方细管时气体的温度;
(2)当气体温度升高到T=600K时,封闭气体的体积。
11.肺活量是常用来衡量人体心肺功能的重要指标。肺活量是指在标准大气压false下人一次尽力吸气后,再尽力呼出的气体体积总量。某同学在学习气体实验定律后,设计了一个吹气球实验来粗测自己肺活量。该同学先尽最大努力吸气,然后通过气球口尽力向气球内吹气,气球没有被吹爆,此时气球可近似看成球形,过一段时间稳定后测得气球的直径falsecm。已知气球橡胶薄膜产生的附加压强false,其中false为薄膜的等效表面张力系数,R为气球充气后的半径。如图为该气球的等效表面张力系数false随气球半径R的变化曲线。吹气前气球内部的空气可忽略不计,空气可看作理想气体,人的体温为37℃,环境温度为27℃,大气压强false,false。求:
(1)吹气后稳定时气球内气体的压强;
(2)该同学的肺活量为多少毫升。
12.导热良好、粗细均匀的U形玻璃管竖直放置,左端封闭,右端开口初始时,管内水银柱及空气柱长度如图所示,下方水银柱足够长且左、右两侧水银面等高。已知大气压强false保持不变,环境初始温度为false。现缓慢将玻璃管处环境温度提升至false。求:
(1)右侧空气柱长度;
(2)左侧管内水银面下降的高度。
13.如图所示,上端开口的内壁光滑圆柱形汽缸固定在倾角为30°的斜面上,一上端固定的轻弹簧与横截面积为40cm2的活塞相连接,汽缸内封闭一定质量的理想气体。在汽缸内距缸底60cm处有卡环,活塞只能向上滑动。开始时活塞搁在卡环上,且弹簧处于原长,缸内气体的压强等于大气压强p0=1.0×105Pa,温度为300 K。现对汽缸内的气体缓慢加热,当温度增加30K时,活塞恰好离开卡环,当温度增加到480K时,活塞移动了20cm。已知g=10m/s2,求:
(1)活塞的质量;
(2)弹簧的劲度系数k。
8.3理想气体的状态方程
1.如图所示,一导热性良好的汽缸内用活塞封住一定量的气体(不计活塞与缸壁摩擦),温度升高时,下列物理量发生变化的是( )
A.活塞高度h B.汽缸高度H
C.气体压强p D.弹簧长度L
【答案】B
【解析】AD.根据整体法分析可知,弹簧的拉力大小等于活塞、汽缸以及气体重力之和,所以当温度升高时,弹簧拉力大小不变,根据胡克定律可知弹簧伸长量不变,即弹簧长度L不变,根据长度关系分析可知,活塞高度h也不变,故AD不符合题意;
C.对活塞单独进行受力分析,由题意及上述分析可知活塞受力情况不变,则气体压强p不变,故C不符合题意;
B.根据理想气体状态方程false=C可知,当T增大且p不变时,气体体积V增大,所以汽缸将向下运动,则汽缸高度H减小,故B符合题意。
故选B。
2.某同学设计了如图所示测量液体密度的装置:左侧为上端开口的圆柱形玻璃缸右侧为上端封闭、高为L0=52cm的玻璃管,两容器底部用细管相连,且左侧玻璃缸横截面积远远大于右侧玻璃管横截面积,两容器导热性能良好。环境温度T=300K。现向左侧玻璃缸缓慢注入待测液体,将原长为L0的空气柱封闭在玻璃管中,当左侧液面高度h1=52cm时,右管内液柱高度h2=2cm。已知大气压强p0=1.0×105Pa,重力加速度g取10m/s2
①求待测液体的密度;
②将右侧玻璃管内气体温度缓慢升高,当右管内液体刚好全部挤出时,求管内空气的温度。(计算结果保留三位有效数字)
【答案】(1)8×102kg/m3;(2)312K
【解析】①设右管横截面积为S,对右管内的气体,由玻意耳定律
p0V0=p1V1
其中
V0=L0S
V1=(L0-h2)S
解得
p1=1.04×105Pa
又
p1=p0+ρg(h1-h2)
解得
ρ=8×102kg/m3
②对右管内的气体,根据理想气体状态方程
false
其中
p2=p0+ρgh1
解得
T′=312K
3.如图所示,一粗细均匀的U形细玻璃管竖直放置并盛有水银,左端封闭一定质量、长度为L=5.0cm的空气,右端足够长且上端开口与大气相通。玻璃管底部有一处于关闭状态的绝热开关K,此时右侧管中的水银面比左侧管中的水银面高h1=16.0cm,现将开关K打开,从玻璃管中缓慢放出部分水银,当左侧水银面比右侧水银面高h2=10.0cm时,将开关K关闭,此时玻璃管内左边空气柱的温度为27℃,并对左侧玻璃管内的空气加热至两边水银柱等高。已知大气压强p0=75.0cmHg。取T=t+273℃,计算结果保留一位小数,求:
(1)放出部分水银后左边封闭空气柱的长度;
(2)两边水银柱的高度相等时,左边空气柱的温度为多少摄氏度?
【答案】(1)7.0cm;(2)320.4℃
【解析】(1)设玻璃管的横截面积为S,放出部分水银后封闭空气柱的长度为L1,压强为p,由玻意耳定律可知
false
由平衡条件可知
false
打开开关K放出部分水银后
false
联立解得
L1=7.0cm
(2)由加热后左右两边水银柱相平可知,左边封闭空气柱的压强
false
加热后左边空气柱的长度
false
根据理想气体状态变化方程可知
false
即
false
解得
false
即
false
4.如图所示,一竖直放置、粗细均匀且足够长的U形玻璃管左端开口,右端通过橡胶管与放在水中导热的球形玻璃容器连通,球形容器连同橡胶管的容积(不变)为V0=80cm3,U形玻璃管中被水银柱封闭有一定质量的理想气体。当环境温度为0℃(热力学温度为273K)时,U形玻璃管右侧水银面比左侧水银面高出h1=18cm,右侧水银柱上方玻璃管长h0=30cm,(已知大气压强p0=76cmHg,U形玻璃管的横截面积为S=0.5cm2)(结果均保留一位小数)
(1)若对水缓慢加热,应加热到多少摄氏度,两边水银柱高度会在同一水平面上?
(2)保持加热后的温度不变,往左管中缓慢注入水银,问注入水银的高度多少时右管水银面回到原来的位置?
【答案】(1)t=118.6℃;(2)25.2cm
【解析】(1)对封闭的气体分析,初状态有
p1=p0-18cmHg=58cmHg
V1=V0+h0S
T1=273K
末状态有
p2=p0
V2=V1+falseS
T2=(273+t)K
由理想气体状态方程有
false
代入数据得
t=118.6℃
(2)当往左管注入水银后,末状态压强为p,体积为
V1=V0+h0S
由玻意耳定律有
p2V2=pV1
解得
p=83.2cmHg
可知往左管注入水银的高度为
h=h1+△h=25.2cm
5.地面上有一高为3h,横截面积为S的圆柱形金属储水容器,该容器与一横截面积不计的竖直细金属水管相连。开始时,容器上方的阀门K打开,容器内水面距容器底部和金属管道出水口高度差如图所示。现关闭容器上方的阀门K,经长时间阳光照射后水管中水面上升了0.1h;然后再打开阀门K,待水面上方空气压强、温度与环境相同后,再用空气泵通过阀门K向容器内注入空气。已知环境空气压强与10h高水柱产生的压强相等,环境温度为T0。充入空气的压强,温度与周围环境相同,充入过程中气体温度不变。不考虑容器内水蒸发对容器内空气压强,温度的影响。求:
(1)经长时间阳光照射后,水面上方空气的温度T;
(2)若要恰好将容器内的水排空,充入容器内的空气体积△V。
【答案】(1)1.01false;(2)false
【解析】(1)由题可知
false
光照后
false
所以
false
金属管横截面积不计属于等体积变化,由查理定律得
false
解得
false
(2)因为水恰好排空,所以最终气体体积
false
false
由理想气体状态方程可得
false
其中
false
所以
false
6.如图所示,一竖直放置的气缸上端开口,气缸壁内有卡口a和b,a、b间距为h=3.0cm,a距缸底的高度为H=12cm,活塞只能在a、b间移动,其下方密封有一定质量的理想气体。已知活塞质量为m=5.0kg,面积为S=1.0×10-3m2,厚度可忽略,活塞和汽缸壁均绝热,不计活塞与气缸间的摩擦。开始时活塞静止于b处,且活塞与卡口刚好没有作用力,气体温度为T0=300K,大气压强为P0=1.0×105Pa。现将一质量也为m的物体轻放在活塞上,活塞刚好到达a处后保持静止。重力加速度大小为g=10m/s2。求:
(1)活塞到达a处后气缸内的压强;
(2)活塞到达a处后气缸内的温度。
【答案】(1)false(2)false
【解析】(1)活塞恰好静止在a处,由平衡得
false
解得
false
同理可得活塞恰好静止在b处
false
解得
false
(2)由理想气体状态方程
false
解得
false
7.如图所示,由内径相同的两U形玻璃管弯接而成的连通器竖直放置,左侧管顶端封闭,右侧管顶开口,中间不漏气。现用水银封闭有A、B两部分气体,已知环境温度恒为17℃,大气压强为76cmHg,稳定时,A部分气体长度为20cm,管内各液面高度差分别为false、false。
(1)求A部分气体的压强;
(2)保持B部分气体温度不变,给A部分气体缓慢加热,使其温度升高到147℃时,A部分气柱长度变为24cm,求此时右侧U形管液面高度差false。
【答案】(1)false;(2)false
【解析】(1)中间B气体压强
false
A部分气体压强
false
(2)A部分气体加热后,有
false
得
false
由于左边水银高度相等,则中间B气体的压强
false
解得
false
8.如图所示,一个足够高绝热的气缸竖直放置,内有一个绝热且光滑的活塞,中间有一个固定的导热性良好的隔板,隔板将气缸分成两部分,分别密封着两部分理想气体A和B。活塞的质量为m,横截面积为S,与隔板相距h。现通过电热丝缓慢加热气体,当A气体吸收热量Q时,活塞上升了false,此时气体的温度为false。已知大气压强为false,重力加速度为g。
①求该加热过程中,气缸内A和B两部分气体的内能增加量之和false;
②气体的温度为false时,停止对气体加热,同时在活塞上缓慢添加砂粒,当活塞恰好回到原来的位置时A气体的温度为false,求此时添加砂粒的总质量false。
【答案】①false;②false
【解析】①气体B的压强为
false
B气体对外做的功
false
由热力学第一定律得
false
解得
false
②B气体的初状态
压强
false
体积
false
温度false
B气体末状态
压强
false
体积
false
温度false
由理想气体状态方程
false
解得
false
9.如图所示,一粗细均匀的U型的玻璃管竖直放置,左侧竖直管上端封闭,右侧竖直管上端与大气相通且足够长,左侧竖直管中封闭一段长为l1=48cm的空气柱(可视为理想气体),气体的温度为T1=300K,水平管内充满水银,右侧竖直管中水银柱长h1=24cm,如果从右侧竖直管内缓慢注入h=36cm水银柱,注入的水银与原来右侧管内水银之间没有空气,注入过程空气柱的温度保持不变,水银柱长度远远大于玻璃管的直径,大气压强为p0=76cmHg。
(1)求稳定后空气柱的长度l2;
(2)如果要使空气柱再恢复到原来的长度48cm,求需要将空气柱的温度变为多少。
【答案】(1)40cm;(2)408K
【解析】(1)初始状态下气体的压强为
false
空气柱长度
false
设玻璃管横截面积为S,气体的体积为
false
设注入水银后水平管进入左侧竖直管内水银长度为x,则气体的压强为
false
气体的体积为
false
注入过程气体温度不变,根据玻意耳定律得
false
解得
false
则稳定后空气柱的长度
false
(2)要使空气柱变为原来长度则气体压强变为
false
根据查理定律
false
解得空气柱的温度变为
false
10.如图所示,上细下粗内壁光滑足够长的玻璃管竖直放置,开口向上,上下管的截面积分别为false。粗管中静止着一段长为false的水银柱,水银柱上表而到细管下端口的距离falsecm,水银柱下端封闭了长为false=30cm的理想气柱。此时管中气体温度T0=300K,大气压强false=75cmHg且恒定不变。现给气体缓慢进行加热,求∶
(1)水银柱恰好全部进入上方细管时气体的温度;
(2)当气体温度升高到T=600K时,封闭气体的体积。
【答案】(1)450K;(2)1600cm3
【解析】(1)气体初态压强
p1=p0+ρgl1=80cmHg
末态压强
p2=p0+ρgl4
其中
l1S1=l4S2
气体满足
false
联立解得
T1=450K
(2)继续升温,气体压强保持不变,有
false
解得
V=1600cm3
11.肺活量是常用来衡量人体心肺功能的重要指标。肺活量是指在标准大气压false下人一次尽力吸气后,再尽力呼出的气体体积总量。某同学在学习气体实验定律后,设计了一个吹气球实验来粗测自己肺活量。该同学先尽最大努力吸气,然后通过气球口尽力向气球内吹气,气球没有被吹爆,此时气球可近似看成球形,过一段时间稳定后测得气球的直径falsecm。已知气球橡胶薄膜产生的附加压强false,其中false为薄膜的等效表面张力系数,R为气球充气后的半径。如图为该气球的等效表面张力系数false随气球半径R的变化曲线。吹气前气球内部的空气可忽略不计,空气可看作理想气体,人的体温为37℃,环境温度为27℃,大气压强false,false。求:
(1)吹气后稳定时气球内气体的压强;
(2)该同学的肺活量为多少毫升。
【答案】(1)false;(2)false
【解析】(1)由图像可知气球半径
false
则气球橡胶薄膜的等效表面张力系数
false
吹气后稳定时气球内气体的压强
false
解得
false
(2)设该同学的肺活量为false,由理想气体状态方程得
false
false
解得:
false
12.导热良好、粗细均匀的U形玻璃管竖直放置,左端封闭,右端开口初始时,管内水银柱及空气柱长度如图所示,下方水银柱足够长且左、右两侧水银面等高。已知大气压强false保持不变,环境初始温度为false。现缓慢将玻璃管处环境温度提升至false。求:
(1)右侧空气柱长度;
(2)左侧管内水银面下降的高度。
【答案】(1)5.5cm;(2)1.83cm
【解析】(1) 对右侧气体,初态
false?=90cmHg,false,false
末态
false,false,false
根据
false
解得
false
(2)对左侧气体
false?=90cmHg,false,false
末态
false,false,false
根据理想气体状态方程
false
左侧管内水银面下降的高度
false
13.如图所示,上端开口的内壁光滑圆柱形汽缸固定在倾角为30°的斜面上,一上端固定的轻弹簧与横截面积为40cm2的活塞相连接,汽缸内封闭一定质量的理想气体。在汽缸内距缸底60cm处有卡环,活塞只能向上滑动。开始时活塞搁在卡环上,且弹簧处于原长,缸内气体的压强等于大气压强p0=1.0×105Pa,温度为300 K。现对汽缸内的气体缓慢加热,当温度增加30K时,活塞恰好离开卡环,当温度增加到480K时,活塞移动了20cm。已知g=10m/s2,求:
(1)活塞的质量;
(2)弹簧的劲度系数k。
【答案】(1)8kg;(2)200N/m
【解析】(1)气体温度从300K增加到330K的过程中,经历等容变化,则有
false
解得:false;
此时,活塞恰好离开卡环,可得:
false
解得:false;
(2)气体温度从330K增加到480K的过程中,则
false
解得:false;
对活塞受力分析可得
false
解得:false。
