第5章生活中的轴对称 期末综合复习训练2-2020-2021学年北师大版七年级数学下册(word版含答案)
文档属性
| 名称 | 第5章生活中的轴对称 期末综合复习训练2-2020-2021学年北师大版七年级数学下册(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 311.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 18:50:58 | ||
图片预览


文档简介
2021年北师大版七年级数学下册《第5章生活中的轴对称》期末综合复习训练2(附答案)
1.到三角形三边的距离相等的是( )
A.三条中线交点 B.三条角平分线的交点
C.三条高的交点 D.三条中垂线的交点
2.如图,在△ABC中,点D在边BC上,且满足AB=AD=DC,过点D作DE⊥AD,交AC于点E.设∠BAD=α,∠CAD=β,∠CDE=γ,则( )
A.2α+3β=180° B.3α+2β=180° C.β+2γ=90° D.2β+γ=90°
3.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,CF⊥AB,交AB于点F,交BE于点D,若BC=8cm,DF=3cm,则△CDB的面积为( )
A.12cm2 B.8cm2 C.6cm2 D.4cm2
4.如图,阴影部分是由3个小正方形组成的一个图形,若在图中剩余的方格中涂黑一个正方形,使整个阴影部分成为轴对称图形,涂法有( )
A.2种 B.3种 C.4种 D.5种
5.如图,四边形ABCD中,CD=3,AD=5,AC的垂直平分线交AD于E,则△CDE的周长是( )
A.6 B.8 C.9 D.10
6.下列图案不是轴对称图形的是( )
A. B. C. D.
7.下面4个汉字中,是轴对称图形的是( )
A. B. C. D.
8.已知等腰三角形的两边长分别为2和5,则该等腰三角形的周长为( )
A.7 B.9 C.9或12 D.12
9.将矩形ABCD按如图方式折叠:BE,EG,FG为折痕,若顶点A,C,D都落在点O处,且点B,O,G在同一直线上,同时点E,O,F在另一条直线上.请完成下列探究:
(1)∠BEG的大小为 ;
(2)若AD=4,则四边形BEGF的面积为 .
10.如图,等腰△ABC的底边BC长为4,面积是16,腰AB的垂直平分线EF分别交AB、AC于点F、E,若点D为BC边上的中点,M为线段EF上一动点,则△BDM的周长的最小值是 .
11.在△ABC中,∠B=80°,过点A作一条直线,将△ABC分成两个新的三角形,若这两个三角形都是等腰三角形,则∠C的度数为 .
12.如图,△ABD和△ABC关于直线AD对称,若S△ABC=12,则图中阴影部分面积为 .
13.等腰△ABC中,BD是AC边上的高,且BD=AC,则等腰△ABC底角的度数为 .
14.在△ABC中,D、E是边BC上的两点,DC=DA,EA=EB,∠DAE=40°,则∠BAC的度数是 .
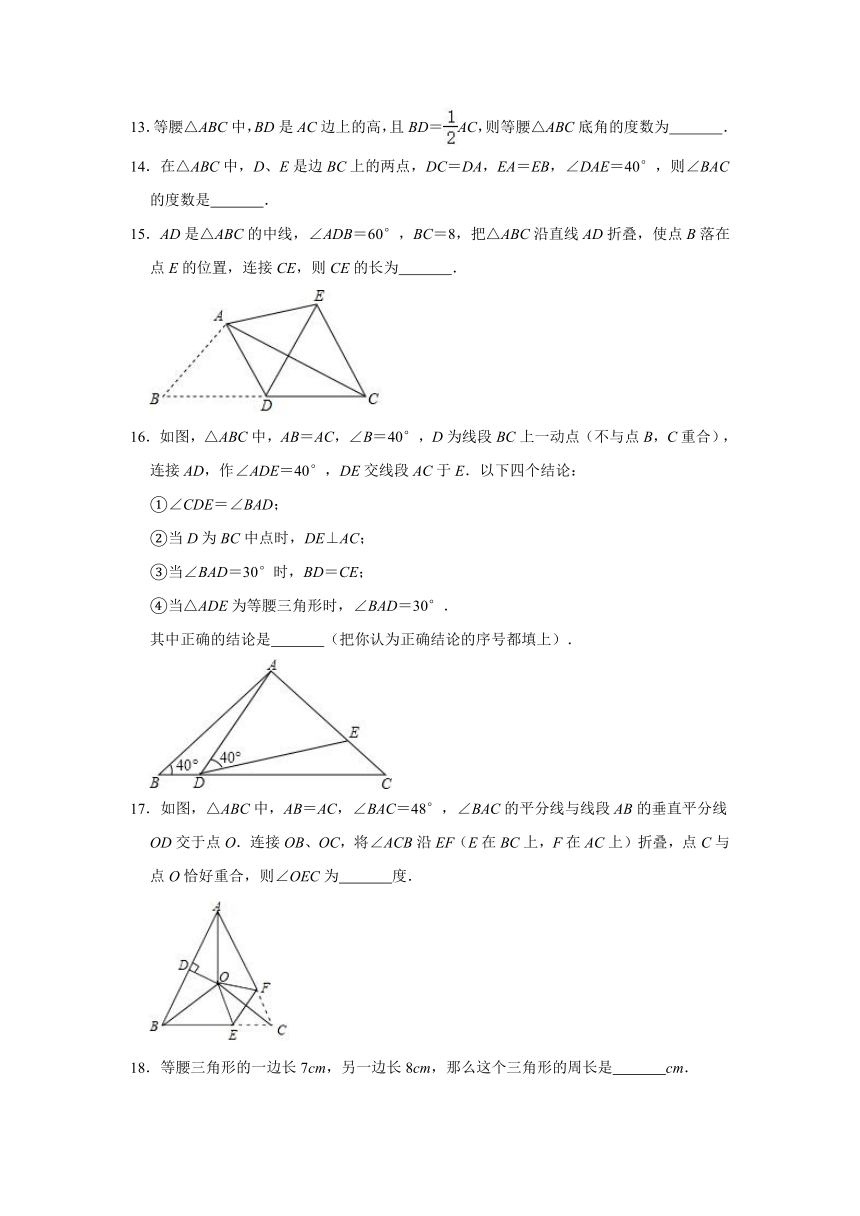
15.AD是△ABC的中线,∠ADB=60°,BC=8,把△ABC沿直线AD折叠,使点B落在点E的位置,连接CE,则CE的长为 .
16.如图,△ABC中,AB=AC,∠B=40°,D为线段BC上一动点(不与点B,C重合),连接AD,作∠ADE=40°,DE交线段AC于E.以下四个结论:
①∠CDE=∠BAD;
②当D为BC中点时,DE⊥AC;
③当∠BAD=30°时,BD=CE;
④当△ADE为等腰三角形时,∠BAD=30°.
其中正确的结论是 (把你认为正确结论的序号都填上).
17.如图,△ABC中,AB=AC,∠BAC=48°,∠BAC的平分线与线段AB的垂直平分线OD交于点O.连接OB、OC,将∠ACB沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为 度.
18.等腰三角形的一边长7cm,另一边长8cm,那么这个三角形的周长是 cm.
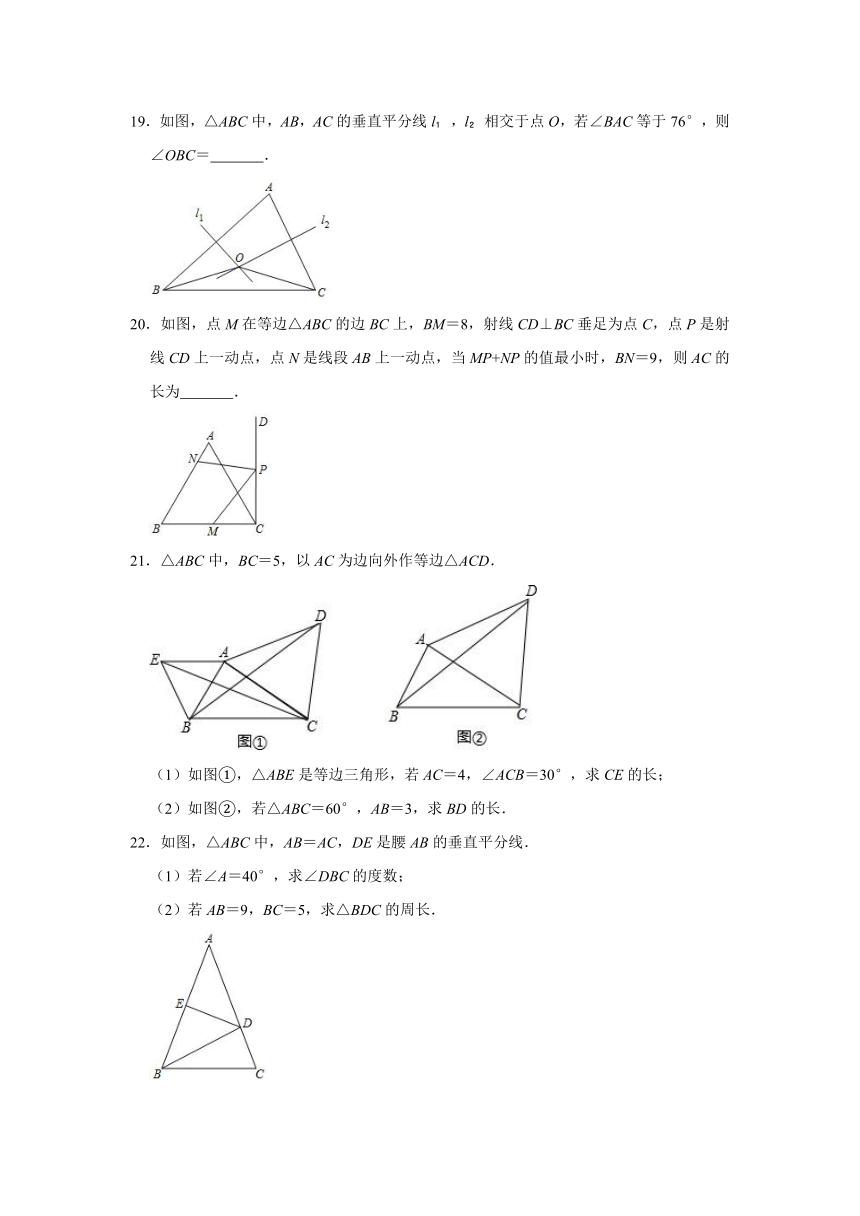
19.如图,△ABC中,AB,AC的垂直平分线l?,l?相交于点O,若∠BAC等于76°,则∠OBC= .
20.如图,点M在等边△ABC的边BC上,BM=8,射线CD⊥BC垂足为点C,点P是射线CD上一动点,点N是线段AB上一动点,当MP+NP的值最小时,BN=9,则AC的长为 .
21.△ABC中,BC=5,以AC为边向外作等边△ACD.
(1)如图①,△ABE是等边三角形,若AC=4,∠ACB=30°,求CE的长;
(2)如图②,若△ABC=60°,AB=3,求BD的长.
22.如图,△ABC中,AB=AC,DE是腰AB的垂直平分线.
(1)若∠A=40°,求∠DBC的度数;
(2)若AB=9,BC=5,求△BDC的周长.
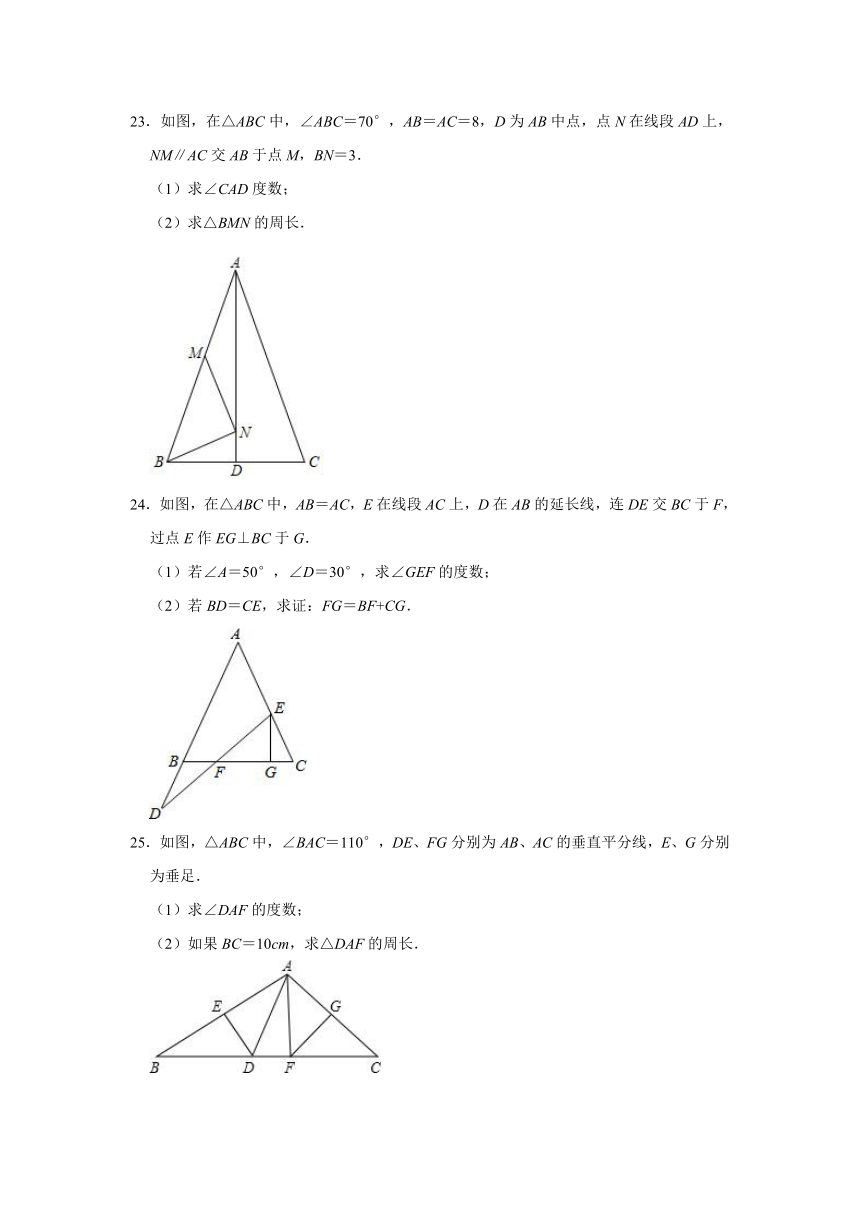
23.如图,在△ABC中,∠ABC=70°,AB=AC=8,D为AB中点,点N在线段AD上,NM∥AC交AB于点M,BN=3.
(1)求∠CAD度数;
(2)求△BMN的周长.
24.如图,在△ABC中,AB=AC,E在线段AC上,D在AB的延长线,连DE交BC于F,过点E作EG⊥BC于G.
(1)若∠A=50°,∠D=30°,求∠GEF的度数;
(2)若BD=CE,求证:FG=BF+CG.
25.如图,△ABC中,∠BAC=110°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.
(1)求∠DAF的度数;
(2)如果BC=10cm,求△DAF的周长.
26.如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
(1)说明BE=CF的理由;
(2)如果AB=5,AC=3,求AE、BE的长.
27.如图,已知在△ABC中,AB=AC,D是BC边上任意一点,E在AC边上,且AD=AE.
(1)若∠BAD=40°,求∠EDC的度数;
(2)若∠EDC=15°,求∠BAD的度数;
(3)根据上述两小题的答案,试探索∠EDC与∠BAD的关系.
28.如图所示,△ABC中,AB=BC,DE⊥AB于点E,DF⊥BC于点D,交AC于F.
(1)若∠AFD=155°,求∠EDF的度数;
(2)若点F是AC的中点,求证:∠CFD=∠B.
参考答案
1.解:在三角形内部,到三角形三边距离相等的点是三角形三条角平分线的交点,
故选:B.
2.解:∵AB=AD=DC,∠BAD=α,
∴∠B=∠ADB,∠C=∠CAD=β,
∵DE⊥AD,
∴∠ADE=90°,
∴∠CAD+∠AED=90°,
∵∠CDE=γ,∠AED=∠C+∠CDE,
∴∠AED=γ+β,
∴2β+γ=90°,
故选:D.
3.解:作DH⊥BC与点H,如图:
∵BE平分∠ABC,CF⊥AB,DH⊥BC.
∴DH=DF.
∵DF=3cm.
∴DH=3cm.
∵BC=8cm.
∴△CDB的面积为:=12cm2.
故选:A.
4.解:如图所示:在图中剩余的方格中涂黑一个正方形,使整个阴影部分成为轴对称图形,只要将1,2,3,4处涂黑,都是符合题意的图形.
故选:C.
5.解:∵AC的垂直平分线交AD于E,
∴AE=CE,
∴△CDE的周长是:DE+DE+CE=DC+DE+AE=DC+AD=3+5=8.
故选:B.
6.解:A、不是轴对称图形,故此选项符合题意;
B、是轴对称图形,故此选项不合题意;
C、是轴对称图形,故此选项不合题意;
D、是轴对称图形,故此选项不符合题意;
故选:A.
7.解:A、“爱”字不是轴对称图形;
B、“国”字不是轴对称图形;
C、“敬”字不是轴对称图形;
D、“业”字是轴对称图形;
故选:D.
8.解:当2为腰时,三边为2,2,5,由三角形三边关系定理可知,不能构成三角形,
当5为腰时,三边为5,5,2,符合三角形三边关系定理,周长为:5+5+2=12.
故选:D.
9.解:(1)由折叠可得:∠AEB=∠BEO,∠DEG=∠GEO,
∵∠AEB=∠BEO+∠DEG=∠GEO=180°,
∴∠BEG=90°,
故答案为90°;
(2)由折叠可得,AE=OE=DE,CG=OG=DG,
∴E,G分别为AD,CD的中点,
设DG=CG=a,则AB=2a=OB,DG=OG=CG=a,BG=3a,BC=AD=4,
∵∠C=90°,
∴Rt△BCG中,CG2+BC2=BG2,
∴a2+42=(3a)2,
∴a=,
∴DG=CG=,
∴BG=OB+OG=2+=3,
由折叠可得∠EGD=∠EGO,∠OGF=∠FGC,
∴∠EGF=90°,
∴∠EGD+∠FGC=90°,
∵∠EGD+∠DEG=90°,
∴∠FGC=∠DEG,
∵∠EDG=∠GCF=90°,
∴CF=1,
∴FO=1,
∴EF=3,
∵点B,O,G在同一条直线上,
∴EF⊥BG,
∴S四边形EBFG=×BG×EF=×3×3=.
故答案为:.
10.解:如图,连接AD.
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=?BC?AD=×4×AD=16.
∴AD=8.
∵EF是线段AB的垂直平分线,
∴点B关于直线EF的对称点为点A,
∴AD的长为BM+MD的最小值,
∴△BDM的周长最短=(BM+MD)+BD=AD+BC=6+×8=10.
故答案为:10.
11.解:设过点A且将△ABC分成两个等腰三角形的直线交BC于点D,分三种情况讨论.
①当∠B为等腰△ADB的顶角时,如图1,
∵∠BAD=∠BDA=×(180°﹣80°)=50°,
又∵△ADC是等腰三角形,DA=DC,
∴∠C=∠ADB=25°;
②当∠ADB为等腰△ADB的顶角时,如图2,
∵AD=BD,∠B=80°,
∴∠BAD=∠B=80°,
∴∠ADB=180°﹣80°×2=20°,
又∵△ADC是等腰三角形,DA=DC,
∴∠C=∠ADB=10°;
③当∠DAB为等腰△ADB的顶角时,如图3,
则∠ADB=∠B=80°,
又∵△ADC是等腰三角形,DA=DC,
∴∠C=∠ADB=40°.
故答案为:10°或25°或40°.
12.解:∵△ABD和△ABC关于直线AD对称,
∴S△BEF=S△CEF,
∴S阴=S△ADC=S△ABC=6.
故答案为:6.
13.解:①如图1,当点B是顶角顶点时,
∵AB=BC,BD⊥AC,
∴AD=CD,
∵BD=AC,
∴BD=AD=CD,
在Rt△ABD中,∠A=∠ABD=×(180°﹣90°)=45°;
②如图2,当点B是底角顶点,且BD在△ABC外部时,
∵BD=AC,AC=BC,
∴BD=BC,
∴∠BCD=30°,
∴∠ABC=∠BAC=×30°=15°;
③如图3,当点B是底角顶点,且BD在△ABC内部时,
∵BD=AC,AC=BC,
∴BD=BC,
∴∠C=30°,
∴∠ABC=∠BAC=(180°﹣30°)=75°;
故答案为:15°或45°或75°.
14.解:如图1,∵DC=DA,EA=EB,
∴∠EAB=∠B,∠DAC=∠C,
∠EAB+∠B+∠DAC+∠C+∠DAE=180°,
则2(∠B+∠C)=140°,
解得,∠B+∠C=70°,
∴∠BAC=110°;
如图2,∵DC=DA,EA=EB,∠DAE=40°,
∴∠EAB=∠B,∠DAC=∠C,
∠EAB+∠B+∠DAC+∠C﹣∠DAE=180°,
则2(∠B+∠C)=220°,
解得,∠B+∠C=110°,
∴∠BAC=70°,
故答案为:70°或110°.
15.解:由翻折可知,DB=DE,∠ADB=∠ADE=60°,
∴∠EDC=180°﹣2×60°=60°
∵BD=DC=BC=4,
∴DE=DC,
∴△EDC是等边三角形,
∴CE=CD=4,
故答案为4.
16.解:①∵AB=AC,
∴∠B=∠C=40°,
∴∠BAD=180°﹣40°﹣∠ADB,∠CDE=180°﹣40°﹣∠ADB,
∴∠BAD=∠CDE;故①正确;
②∵D为BC中点,AB=AC,
∴AD⊥BC,
∴∠ADC=90°,
∴∠CDE=50°,
∵∠C=40°,
∴∠DEC=90°,
∴DE⊥AC,故②正确;
③∵∠BAD=30°,
∴∠CDE=30°,
∴∠ADC=70°,
∴∠CAD=180°﹣70°﹣40°=70°,
∴∠DAC=∠ADC,
∴CD=AC,
∵AB=AC,
∴CD=AB,
∴△ABD≌△DCE(ASA),
∴BD=CE;故③正确;
④∵∠C=40°,
∴∠AED>40°,
∴∠ADE≠∠AED,
∵△ADE为等腰三角形,
∴AE=DE,
∴∠DAE=∠ADE=40°,
∵∠BAC=180°﹣40°﹣40°=100°,
∴∠BAD=60°,故④错误,
故答案为:①②③.
17.解:∵∠BAC=48°,AO为∠BAC的平分线,
∴∠BAO=∠BAC=×48°=24°,
∵AB=AC,
∴∠ABC=(180°﹣∠BAC)=(180°﹣48°)=66°,
∵DO是AB的垂直平分线,
∴OA=OB,
∴∠ABO=∠BAO=24°,
∴∠OBC=∠ABC﹣∠ABO=66°﹣24°=42°,
在△AOB和△AOC中,
∴△AOB≌△AOC(SAS),
∴OB=OC,
∴∠OCB=∠OBC=42°,
由折叠的性质可知,OE=CE,
∴∠COE=∠OCB=42°,
在△OCE中,∠OEC=180°﹣∠COE﹣∠OCB=180°﹣42°﹣42°=96°,
故答案为:96.
18.解:分两种情况讨论:
当这个三角形的底边是7cm时,三角形的三边分别是7cm、8cm、8cm,能组成三角形,则三角形的周长是23cm;
当这个三角形的底边是8cm时,三角形的三边分别是7cm、7cm、8cm,能组成三角形,则三角形的周长是22cm.
故等腰三角形的周长是22cm或23cm.
故答案为:22或23.
19.解:连接OA,
∵AB,AC的垂直平分线l?,l?相交于点O,
∴OA=OB,OA=OC,
∴∠OBA=∠OAB,∠OCA=∠OAC,OB=OC,
∴∠OBA+∠OCA=∠BAC=76°,
∴∠OBC+∠OCB=180°﹣∠BAC﹣(∠OBA+∠OCA)=28°,
∵OB=OC,
∴∠OBC=∠OCB=14°,
故答案为:14°.
20.解:∵△ABC是等边三角形,
∴AC=BC,∠B=60°,
作点M关于直线CD的对称点G,过G作GN⊥AB于N,交CD于P,
则此时,MP+PN的值最小,
∵∠B=60°,∠BNG=90°,
∴∠G=30°,
∵BN=9,
∴BG=2BN=18,
∴MG=10,
∴CM=CG=5,
∴AC=BC=13,
故答案为:13.
21.解:(1)∵△ABE与△ACD是等边三角形,
∴AC=AD,AB=AE,
∴∠DCA=∠CAD=∠EAB=60°,
∴∠EAB+∠BAC=∠CAD+∠BAC,
即∠EAC=∠BAD.
在△EAC和△BAD中,
,
∴△EAC≌△BAD(SAS).
∴EC=BD,
又∵∠ACB=30°,
∴∠DCB=∠ACB+∠DCA=90°,
∵CD=AC=4,BC=5,
∴BD===.
∴CE=BD=.
(2)以AB为边向外作等边三角形△ABE,连接线段CE,作EK垂直于CB延长线于点K.
∵△ABE与△ACD是等边三角形,
∴AC=AD,AB=AE,
∴∠DCA=∠CAD=∠EAB=60°,
∴∠EAB+∠BAC=∠CAD+∠BAC,
即∠EAC=∠BAD.
在△EAC和△BAD中,
,
∴△EAC≌△BAD(SAS).
∴EC=BD,
∵∠EBA=∠ABC=60°,
∴∠EBC=∠EBA+∠ABC=120°,
∴∠EBK=180°﹣∠EBC=60°,
∴EK=3×=,
∴KB=3×=,
∴KC=KB+BC=+5=,
在Rt△EKC中,根据勾股定理得,
EC===7.
∴BD=EC=7.
22.解:(1)∵△ABC中,AB=AC,∠A=40°,
∴∠ABC==70°.
∵DE是腰AB的垂直平分线,
∴AD=BD,∠DBA=∠A=40°,
∴∠DBC=70°﹣40°=30°;
(2)由(1)得:AD=BD,
∴△BDC的周长=BD+CD+BC=AD+CD+BC=AC+BC=AB+BC=9+5=14.
答:△BDC的周长是14.
23.解:(1)∵AB=AC,
∴△ABC是等腰三角形,
又∵∠ABC=70°,
∴∠BAC=180°﹣70°×2=40°,
又∵D为AB中点,
∴AD平分∠BAC,
∴∠CAD=∠BAD=∠BAC=×40°=20°,
故∠CAD度数为20°.
(2)∵NM∥AC,
∴∠ANM=∠CAD,
又∵∠CAD=∠BAD,
∴∠ANM=∠BAD,
∴AM=NM,
∴△BMN的周长=MB+BN+NM=AB+BN,
∵AB=8,BN=3,
∴△BMN的周长=8+3=11.
故△BMN的周长为11.
24.(1)解:∵∠A=50°,
∴∠C=(180°﹣∠A)=(180°﹣50°)=65°,
∵EG⊥BC,
∴∠CEG=90°﹣∠C=90°﹣65°=25°,
∵∠A=50°,∠D=30°,
∴∠CEF=∠A+∠D=50°+30°=80°,
∴∠GEF=∠CEF﹣∠CEG=80°﹣25°=55°;
(2)证明:过点E作EH∥AB交BC于H,
则∠ABC=∠EHC,∠D=∠FEH,
∵AB=AC,
∴∠ABC=∠C,
∴∠EHC=∠C,
∴EC=EH,
∵BD=CE,
∴BD=EH,
在△BDF和△HEF中,
,
∴△BDF≌△HEF(AAS),
∴BF=FH,
又∵EC=EH,EG⊥BC,
∴CG=HG,
∴FG=FH+HG=BF+CG.
25.解:(1)设∠B=x,∠C=y.
∵∠BAC+∠B+∠C=180°,
∴110°+∠B+∠C=180°,
∴x+y=70°.
∵AB、AC的垂直平分线分别交BA于E、交AC于G,
∴DA=BD,FA=FC,
∴∠EAD=∠B,∠FAC=∠C.
∴∠DAF=∠BAC﹣(x+y)=110°﹣70°=40°.
(2)∵AB、AC的垂直平分线分别交BA于E、交AC于G,
∴DA=BD,FA=FC,
∴△DAF的周长为:AD+DF+AF=BD+DF+FC=BC=10(cm).
26.(1)证明:连接BD,CD,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠BED=∠CFD=90°,
∵DG⊥BC且平分BC,
∴BD=CD,
在Rt△BED与Rt△CFD中,
,
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF;
(2)解:在△AED和△AFD中,
,
∴△AED≌△AFD(AAS),
∴AE=AF,
设BE=x,则CF=x,
∵AB=5,AC=3,AE=AB﹣BE,AF=AC+CF,
∴5﹣x=3+x,
解得:x=1,
∴BE=1,AE=AB﹣BE=5﹣1=4.
27.解:(1)∵AB=AC,
∴∠B=∠C=(180°﹣∠BAC)=90°﹣∠BAC,
∴∠ADC=∠B+∠BAD=90°﹣∠BAC+40°=130°﹣∠BAC,
∵∠DAC=∠BAC﹣∠BAD=∠BAC﹣40°,
∴∠ADE=∠AED=(180°﹣∠DAC)=110°﹣∠BAC,
∴∠EDC=∠ADC﹣∠ADE=(130°﹣∠BAC)﹣(110°﹣∠BAC)=20°,
故∠EDC的度数是20°.
(2)∠AED=∠EDC+∠C,∠ADC=∠B+∠BAD,
∵AD=AE,
∴∠AED=∠ADE,
∵AB=AC,
∴∠B=∠C,
∴∠B+∠BAD=∠EDC+∠C+∠EDC,
即∠BAD=2∠EDC,
∵∠EDC=15°,
∴∠BAD=30°.
(3)∠EDC与∠BAD的数量关系是∠EDC=∠BAD.
28.解:(1)∵∠AFD=155°,
∴∠DFC=25°,
∵DF⊥BC,DE⊥AB,
∴∠FDC=∠AED=90°,
在Rt△FDC中,
∴∠C=90°﹣25°=65°,
∵AB=BC,
∴∠C=∠A=65°,
∴∠EDF=360°﹣65°﹣155°﹣90°=50°.
(2)连接BF
∵AB=BC,且点F是AC的中点,
∴BF⊥AC,∠ABF=∠CBF=∠ABC,
∴∠CFD+∠BFD=90°,
∠CBF+∠BFD=90°,
∴∠CFD=∠CBF,
∴∠CFD=∠ABC.
1.到三角形三边的距离相等的是( )
A.三条中线交点 B.三条角平分线的交点
C.三条高的交点 D.三条中垂线的交点
2.如图,在△ABC中,点D在边BC上,且满足AB=AD=DC,过点D作DE⊥AD,交AC于点E.设∠BAD=α,∠CAD=β,∠CDE=γ,则( )
A.2α+3β=180° B.3α+2β=180° C.β+2γ=90° D.2β+γ=90°
3.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,CF⊥AB,交AB于点F,交BE于点D,若BC=8cm,DF=3cm,则△CDB的面积为( )
A.12cm2 B.8cm2 C.6cm2 D.4cm2
4.如图,阴影部分是由3个小正方形组成的一个图形,若在图中剩余的方格中涂黑一个正方形,使整个阴影部分成为轴对称图形,涂法有( )
A.2种 B.3种 C.4种 D.5种
5.如图,四边形ABCD中,CD=3,AD=5,AC的垂直平分线交AD于E,则△CDE的周长是( )
A.6 B.8 C.9 D.10
6.下列图案不是轴对称图形的是( )
A. B. C. D.
7.下面4个汉字中,是轴对称图形的是( )
A. B. C. D.
8.已知等腰三角形的两边长分别为2和5,则该等腰三角形的周长为( )
A.7 B.9 C.9或12 D.12
9.将矩形ABCD按如图方式折叠:BE,EG,FG为折痕,若顶点A,C,D都落在点O处,且点B,O,G在同一直线上,同时点E,O,F在另一条直线上.请完成下列探究:
(1)∠BEG的大小为 ;
(2)若AD=4,则四边形BEGF的面积为 .
10.如图,等腰△ABC的底边BC长为4,面积是16,腰AB的垂直平分线EF分别交AB、AC于点F、E,若点D为BC边上的中点,M为线段EF上一动点,则△BDM的周长的最小值是 .
11.在△ABC中,∠B=80°,过点A作一条直线,将△ABC分成两个新的三角形,若这两个三角形都是等腰三角形,则∠C的度数为 .
12.如图,△ABD和△ABC关于直线AD对称,若S△ABC=12,则图中阴影部分面积为 .
13.等腰△ABC中,BD是AC边上的高,且BD=AC,则等腰△ABC底角的度数为 .
14.在△ABC中,D、E是边BC上的两点,DC=DA,EA=EB,∠DAE=40°,则∠BAC的度数是 .
15.AD是△ABC的中线,∠ADB=60°,BC=8,把△ABC沿直线AD折叠,使点B落在点E的位置,连接CE,则CE的长为 .
16.如图,△ABC中,AB=AC,∠B=40°,D为线段BC上一动点(不与点B,C重合),连接AD,作∠ADE=40°,DE交线段AC于E.以下四个结论:
①∠CDE=∠BAD;
②当D为BC中点时,DE⊥AC;
③当∠BAD=30°时,BD=CE;
④当△ADE为等腰三角形时,∠BAD=30°.
其中正确的结论是 (把你认为正确结论的序号都填上).
17.如图,△ABC中,AB=AC,∠BAC=48°,∠BAC的平分线与线段AB的垂直平分线OD交于点O.连接OB、OC,将∠ACB沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为 度.
18.等腰三角形的一边长7cm,另一边长8cm,那么这个三角形的周长是 cm.
19.如图,△ABC中,AB,AC的垂直平分线l?,l?相交于点O,若∠BAC等于76°,则∠OBC= .
20.如图,点M在等边△ABC的边BC上,BM=8,射线CD⊥BC垂足为点C,点P是射线CD上一动点,点N是线段AB上一动点,当MP+NP的值最小时,BN=9,则AC的长为 .
21.△ABC中,BC=5,以AC为边向外作等边△ACD.
(1)如图①,△ABE是等边三角形,若AC=4,∠ACB=30°,求CE的长;
(2)如图②,若△ABC=60°,AB=3,求BD的长.
22.如图,△ABC中,AB=AC,DE是腰AB的垂直平分线.
(1)若∠A=40°,求∠DBC的度数;
(2)若AB=9,BC=5,求△BDC的周长.
23.如图,在△ABC中,∠ABC=70°,AB=AC=8,D为AB中点,点N在线段AD上,NM∥AC交AB于点M,BN=3.
(1)求∠CAD度数;
(2)求△BMN的周长.
24.如图,在△ABC中,AB=AC,E在线段AC上,D在AB的延长线,连DE交BC于F,过点E作EG⊥BC于G.
(1)若∠A=50°,∠D=30°,求∠GEF的度数;
(2)若BD=CE,求证:FG=BF+CG.
25.如图,△ABC中,∠BAC=110°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.
(1)求∠DAF的度数;
(2)如果BC=10cm,求△DAF的周长.
26.如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
(1)说明BE=CF的理由;
(2)如果AB=5,AC=3,求AE、BE的长.
27.如图,已知在△ABC中,AB=AC,D是BC边上任意一点,E在AC边上,且AD=AE.
(1)若∠BAD=40°,求∠EDC的度数;
(2)若∠EDC=15°,求∠BAD的度数;
(3)根据上述两小题的答案,试探索∠EDC与∠BAD的关系.
28.如图所示,△ABC中,AB=BC,DE⊥AB于点E,DF⊥BC于点D,交AC于F.
(1)若∠AFD=155°,求∠EDF的度数;
(2)若点F是AC的中点,求证:∠CFD=∠B.
参考答案
1.解:在三角形内部,到三角形三边距离相等的点是三角形三条角平分线的交点,
故选:B.
2.解:∵AB=AD=DC,∠BAD=α,
∴∠B=∠ADB,∠C=∠CAD=β,
∵DE⊥AD,
∴∠ADE=90°,
∴∠CAD+∠AED=90°,
∵∠CDE=γ,∠AED=∠C+∠CDE,
∴∠AED=γ+β,
∴2β+γ=90°,
故选:D.
3.解:作DH⊥BC与点H,如图:
∵BE平分∠ABC,CF⊥AB,DH⊥BC.
∴DH=DF.
∵DF=3cm.
∴DH=3cm.
∵BC=8cm.
∴△CDB的面积为:=12cm2.
故选:A.
4.解:如图所示:在图中剩余的方格中涂黑一个正方形,使整个阴影部分成为轴对称图形,只要将1,2,3,4处涂黑,都是符合题意的图形.
故选:C.
5.解:∵AC的垂直平分线交AD于E,
∴AE=CE,
∴△CDE的周长是:DE+DE+CE=DC+DE+AE=DC+AD=3+5=8.
故选:B.
6.解:A、不是轴对称图形,故此选项符合题意;
B、是轴对称图形,故此选项不合题意;
C、是轴对称图形,故此选项不合题意;
D、是轴对称图形,故此选项不符合题意;
故选:A.
7.解:A、“爱”字不是轴对称图形;
B、“国”字不是轴对称图形;
C、“敬”字不是轴对称图形;
D、“业”字是轴对称图形;
故选:D.
8.解:当2为腰时,三边为2,2,5,由三角形三边关系定理可知,不能构成三角形,
当5为腰时,三边为5,5,2,符合三角形三边关系定理,周长为:5+5+2=12.
故选:D.
9.解:(1)由折叠可得:∠AEB=∠BEO,∠DEG=∠GEO,
∵∠AEB=∠BEO+∠DEG=∠GEO=180°,
∴∠BEG=90°,
故答案为90°;
(2)由折叠可得,AE=OE=DE,CG=OG=DG,
∴E,G分别为AD,CD的中点,
设DG=CG=a,则AB=2a=OB,DG=OG=CG=a,BG=3a,BC=AD=4,
∵∠C=90°,
∴Rt△BCG中,CG2+BC2=BG2,
∴a2+42=(3a)2,
∴a=,
∴DG=CG=,
∴BG=OB+OG=2+=3,
由折叠可得∠EGD=∠EGO,∠OGF=∠FGC,
∴∠EGF=90°,
∴∠EGD+∠FGC=90°,
∵∠EGD+∠DEG=90°,
∴∠FGC=∠DEG,
∵∠EDG=∠GCF=90°,
∴CF=1,
∴FO=1,
∴EF=3,
∵点B,O,G在同一条直线上,
∴EF⊥BG,
∴S四边形EBFG=×BG×EF=×3×3=.
故答案为:.
10.解:如图,连接AD.
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=?BC?AD=×4×AD=16.
∴AD=8.
∵EF是线段AB的垂直平分线,
∴点B关于直线EF的对称点为点A,
∴AD的长为BM+MD的最小值,
∴△BDM的周长最短=(BM+MD)+BD=AD+BC=6+×8=10.
故答案为:10.
11.解:设过点A且将△ABC分成两个等腰三角形的直线交BC于点D,分三种情况讨论.
①当∠B为等腰△ADB的顶角时,如图1,
∵∠BAD=∠BDA=×(180°﹣80°)=50°,
又∵△ADC是等腰三角形,DA=DC,
∴∠C=∠ADB=25°;
②当∠ADB为等腰△ADB的顶角时,如图2,
∵AD=BD,∠B=80°,
∴∠BAD=∠B=80°,
∴∠ADB=180°﹣80°×2=20°,
又∵△ADC是等腰三角形,DA=DC,
∴∠C=∠ADB=10°;
③当∠DAB为等腰△ADB的顶角时,如图3,
则∠ADB=∠B=80°,
又∵△ADC是等腰三角形,DA=DC,
∴∠C=∠ADB=40°.
故答案为:10°或25°或40°.
12.解:∵△ABD和△ABC关于直线AD对称,
∴S△BEF=S△CEF,
∴S阴=S△ADC=S△ABC=6.
故答案为:6.
13.解:①如图1,当点B是顶角顶点时,
∵AB=BC,BD⊥AC,
∴AD=CD,
∵BD=AC,
∴BD=AD=CD,
在Rt△ABD中,∠A=∠ABD=×(180°﹣90°)=45°;
②如图2,当点B是底角顶点,且BD在△ABC外部时,
∵BD=AC,AC=BC,
∴BD=BC,
∴∠BCD=30°,
∴∠ABC=∠BAC=×30°=15°;
③如图3,当点B是底角顶点,且BD在△ABC内部时,
∵BD=AC,AC=BC,
∴BD=BC,
∴∠C=30°,
∴∠ABC=∠BAC=(180°﹣30°)=75°;
故答案为:15°或45°或75°.
14.解:如图1,∵DC=DA,EA=EB,
∴∠EAB=∠B,∠DAC=∠C,
∠EAB+∠B+∠DAC+∠C+∠DAE=180°,
则2(∠B+∠C)=140°,
解得,∠B+∠C=70°,
∴∠BAC=110°;
如图2,∵DC=DA,EA=EB,∠DAE=40°,
∴∠EAB=∠B,∠DAC=∠C,
∠EAB+∠B+∠DAC+∠C﹣∠DAE=180°,
则2(∠B+∠C)=220°,
解得,∠B+∠C=110°,
∴∠BAC=70°,
故答案为:70°或110°.
15.解:由翻折可知,DB=DE,∠ADB=∠ADE=60°,
∴∠EDC=180°﹣2×60°=60°
∵BD=DC=BC=4,
∴DE=DC,
∴△EDC是等边三角形,
∴CE=CD=4,
故答案为4.
16.解:①∵AB=AC,
∴∠B=∠C=40°,
∴∠BAD=180°﹣40°﹣∠ADB,∠CDE=180°﹣40°﹣∠ADB,
∴∠BAD=∠CDE;故①正确;
②∵D为BC中点,AB=AC,
∴AD⊥BC,
∴∠ADC=90°,
∴∠CDE=50°,
∵∠C=40°,
∴∠DEC=90°,
∴DE⊥AC,故②正确;
③∵∠BAD=30°,
∴∠CDE=30°,
∴∠ADC=70°,
∴∠CAD=180°﹣70°﹣40°=70°,
∴∠DAC=∠ADC,
∴CD=AC,
∵AB=AC,
∴CD=AB,
∴△ABD≌△DCE(ASA),
∴BD=CE;故③正确;
④∵∠C=40°,
∴∠AED>40°,
∴∠ADE≠∠AED,
∵△ADE为等腰三角形,
∴AE=DE,
∴∠DAE=∠ADE=40°,
∵∠BAC=180°﹣40°﹣40°=100°,
∴∠BAD=60°,故④错误,
故答案为:①②③.
17.解:∵∠BAC=48°,AO为∠BAC的平分线,
∴∠BAO=∠BAC=×48°=24°,
∵AB=AC,
∴∠ABC=(180°﹣∠BAC)=(180°﹣48°)=66°,
∵DO是AB的垂直平分线,
∴OA=OB,
∴∠ABO=∠BAO=24°,
∴∠OBC=∠ABC﹣∠ABO=66°﹣24°=42°,
在△AOB和△AOC中,
∴△AOB≌△AOC(SAS),
∴OB=OC,
∴∠OCB=∠OBC=42°,
由折叠的性质可知,OE=CE,
∴∠COE=∠OCB=42°,
在△OCE中,∠OEC=180°﹣∠COE﹣∠OCB=180°﹣42°﹣42°=96°,
故答案为:96.
18.解:分两种情况讨论:
当这个三角形的底边是7cm时,三角形的三边分别是7cm、8cm、8cm,能组成三角形,则三角形的周长是23cm;
当这个三角形的底边是8cm时,三角形的三边分别是7cm、7cm、8cm,能组成三角形,则三角形的周长是22cm.
故等腰三角形的周长是22cm或23cm.
故答案为:22或23.
19.解:连接OA,
∵AB,AC的垂直平分线l?,l?相交于点O,
∴OA=OB,OA=OC,
∴∠OBA=∠OAB,∠OCA=∠OAC,OB=OC,
∴∠OBA+∠OCA=∠BAC=76°,
∴∠OBC+∠OCB=180°﹣∠BAC﹣(∠OBA+∠OCA)=28°,
∵OB=OC,
∴∠OBC=∠OCB=14°,
故答案为:14°.
20.解:∵△ABC是等边三角形,
∴AC=BC,∠B=60°,
作点M关于直线CD的对称点G,过G作GN⊥AB于N,交CD于P,
则此时,MP+PN的值最小,
∵∠B=60°,∠BNG=90°,
∴∠G=30°,
∵BN=9,
∴BG=2BN=18,
∴MG=10,
∴CM=CG=5,
∴AC=BC=13,
故答案为:13.
21.解:(1)∵△ABE与△ACD是等边三角形,
∴AC=AD,AB=AE,
∴∠DCA=∠CAD=∠EAB=60°,
∴∠EAB+∠BAC=∠CAD+∠BAC,
即∠EAC=∠BAD.
在△EAC和△BAD中,
,
∴△EAC≌△BAD(SAS).
∴EC=BD,
又∵∠ACB=30°,
∴∠DCB=∠ACB+∠DCA=90°,
∵CD=AC=4,BC=5,
∴BD===.
∴CE=BD=.
(2)以AB为边向外作等边三角形△ABE,连接线段CE,作EK垂直于CB延长线于点K.
∵△ABE与△ACD是等边三角形,
∴AC=AD,AB=AE,
∴∠DCA=∠CAD=∠EAB=60°,
∴∠EAB+∠BAC=∠CAD+∠BAC,
即∠EAC=∠BAD.
在△EAC和△BAD中,
,
∴△EAC≌△BAD(SAS).
∴EC=BD,
∵∠EBA=∠ABC=60°,
∴∠EBC=∠EBA+∠ABC=120°,
∴∠EBK=180°﹣∠EBC=60°,
∴EK=3×=,
∴KB=3×=,
∴KC=KB+BC=+5=,
在Rt△EKC中,根据勾股定理得,
EC===7.
∴BD=EC=7.
22.解:(1)∵△ABC中,AB=AC,∠A=40°,
∴∠ABC==70°.
∵DE是腰AB的垂直平分线,
∴AD=BD,∠DBA=∠A=40°,
∴∠DBC=70°﹣40°=30°;
(2)由(1)得:AD=BD,
∴△BDC的周长=BD+CD+BC=AD+CD+BC=AC+BC=AB+BC=9+5=14.
答:△BDC的周长是14.
23.解:(1)∵AB=AC,
∴△ABC是等腰三角形,
又∵∠ABC=70°,
∴∠BAC=180°﹣70°×2=40°,
又∵D为AB中点,
∴AD平分∠BAC,
∴∠CAD=∠BAD=∠BAC=×40°=20°,
故∠CAD度数为20°.
(2)∵NM∥AC,
∴∠ANM=∠CAD,
又∵∠CAD=∠BAD,
∴∠ANM=∠BAD,
∴AM=NM,
∴△BMN的周长=MB+BN+NM=AB+BN,
∵AB=8,BN=3,
∴△BMN的周长=8+3=11.
故△BMN的周长为11.
24.(1)解:∵∠A=50°,
∴∠C=(180°﹣∠A)=(180°﹣50°)=65°,
∵EG⊥BC,
∴∠CEG=90°﹣∠C=90°﹣65°=25°,
∵∠A=50°,∠D=30°,
∴∠CEF=∠A+∠D=50°+30°=80°,
∴∠GEF=∠CEF﹣∠CEG=80°﹣25°=55°;
(2)证明:过点E作EH∥AB交BC于H,
则∠ABC=∠EHC,∠D=∠FEH,
∵AB=AC,
∴∠ABC=∠C,
∴∠EHC=∠C,
∴EC=EH,
∵BD=CE,
∴BD=EH,
在△BDF和△HEF中,
,
∴△BDF≌△HEF(AAS),
∴BF=FH,
又∵EC=EH,EG⊥BC,
∴CG=HG,
∴FG=FH+HG=BF+CG.
25.解:(1)设∠B=x,∠C=y.
∵∠BAC+∠B+∠C=180°,
∴110°+∠B+∠C=180°,
∴x+y=70°.
∵AB、AC的垂直平分线分别交BA于E、交AC于G,
∴DA=BD,FA=FC,
∴∠EAD=∠B,∠FAC=∠C.
∴∠DAF=∠BAC﹣(x+y)=110°﹣70°=40°.
(2)∵AB、AC的垂直平分线分别交BA于E、交AC于G,
∴DA=BD,FA=FC,
∴△DAF的周长为:AD+DF+AF=BD+DF+FC=BC=10(cm).
26.(1)证明:连接BD,CD,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠BED=∠CFD=90°,
∵DG⊥BC且平分BC,
∴BD=CD,
在Rt△BED与Rt△CFD中,
,
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF;
(2)解:在△AED和△AFD中,
,
∴△AED≌△AFD(AAS),
∴AE=AF,
设BE=x,则CF=x,
∵AB=5,AC=3,AE=AB﹣BE,AF=AC+CF,
∴5﹣x=3+x,
解得:x=1,
∴BE=1,AE=AB﹣BE=5﹣1=4.
27.解:(1)∵AB=AC,
∴∠B=∠C=(180°﹣∠BAC)=90°﹣∠BAC,
∴∠ADC=∠B+∠BAD=90°﹣∠BAC+40°=130°﹣∠BAC,
∵∠DAC=∠BAC﹣∠BAD=∠BAC﹣40°,
∴∠ADE=∠AED=(180°﹣∠DAC)=110°﹣∠BAC,
∴∠EDC=∠ADC﹣∠ADE=(130°﹣∠BAC)﹣(110°﹣∠BAC)=20°,
故∠EDC的度数是20°.
(2)∠AED=∠EDC+∠C,∠ADC=∠B+∠BAD,
∵AD=AE,
∴∠AED=∠ADE,
∵AB=AC,
∴∠B=∠C,
∴∠B+∠BAD=∠EDC+∠C+∠EDC,
即∠BAD=2∠EDC,
∵∠EDC=15°,
∴∠BAD=30°.
(3)∠EDC与∠BAD的数量关系是∠EDC=∠BAD.
28.解:(1)∵∠AFD=155°,
∴∠DFC=25°,
∵DF⊥BC,DE⊥AB,
∴∠FDC=∠AED=90°,
在Rt△FDC中,
∴∠C=90°﹣25°=65°,
∵AB=BC,
∴∠C=∠A=65°,
∴∠EDF=360°﹣65°﹣155°﹣90°=50°.
(2)连接BF
∵AB=BC,且点F是AC的中点,
∴BF⊥AC,∠ABF=∠CBF=∠ABC,
∴∠CFD+∠BFD=90°,
∠CBF+∠BFD=90°,
∴∠CFD=∠CBF,
∴∠CFD=∠ABC.
同课章节目录
