2020-2021学年湘教新版八年级下册数学期末练习试题(Word版有答案)
文档属性
| 名称 | 2020-2021学年湘教新版八年级下册数学期末练习试题(Word版有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 342.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 08:53:47 | ||
图片预览

文档简介
2020-2021学年湘教新版八年级下册数学期末练习试题
一.选择题(共10小题,满分40分,每小题4分)
1.下列各组线段中,不能构成直角三角形的是( )
A.1、、
B.、、
C.2、、
D.1、2、
2.下列图形中,是中心对称图形的是( )
A.
B.
C.
D.
3.下列一次函数中,y随x值增大而增大的是( )
A.y=8x﹣7
B.y=6﹣5x
C.y=﹣8﹣x
D.y=(﹣)x
4.社会主义核心价值观知识竞赛成绩结果统计如下表:成绩在91~100分的为优胜者,则优胜者的频率是( )
分段数(分)
61~70
71~80
81~90
91~100
人数(人)
1
19
22
18
A.35%
B.30%
C.20%
D.10%
5.已知点P(a﹣3,a+2)在x轴上,则a=( )
A.﹣2
B.3
C.﹣5
D.5
6.如图,在平行四边形ABCD中,∠C=120°,AD=4,AB=2,点H、G分别是边CD、BC上的动点.连接AH、HG,点E为AH的中点,点F为GH的中点,连接EF.则EF的最大值与最小值的差为( )
A.1
B.﹣1
C.
D.2﹣
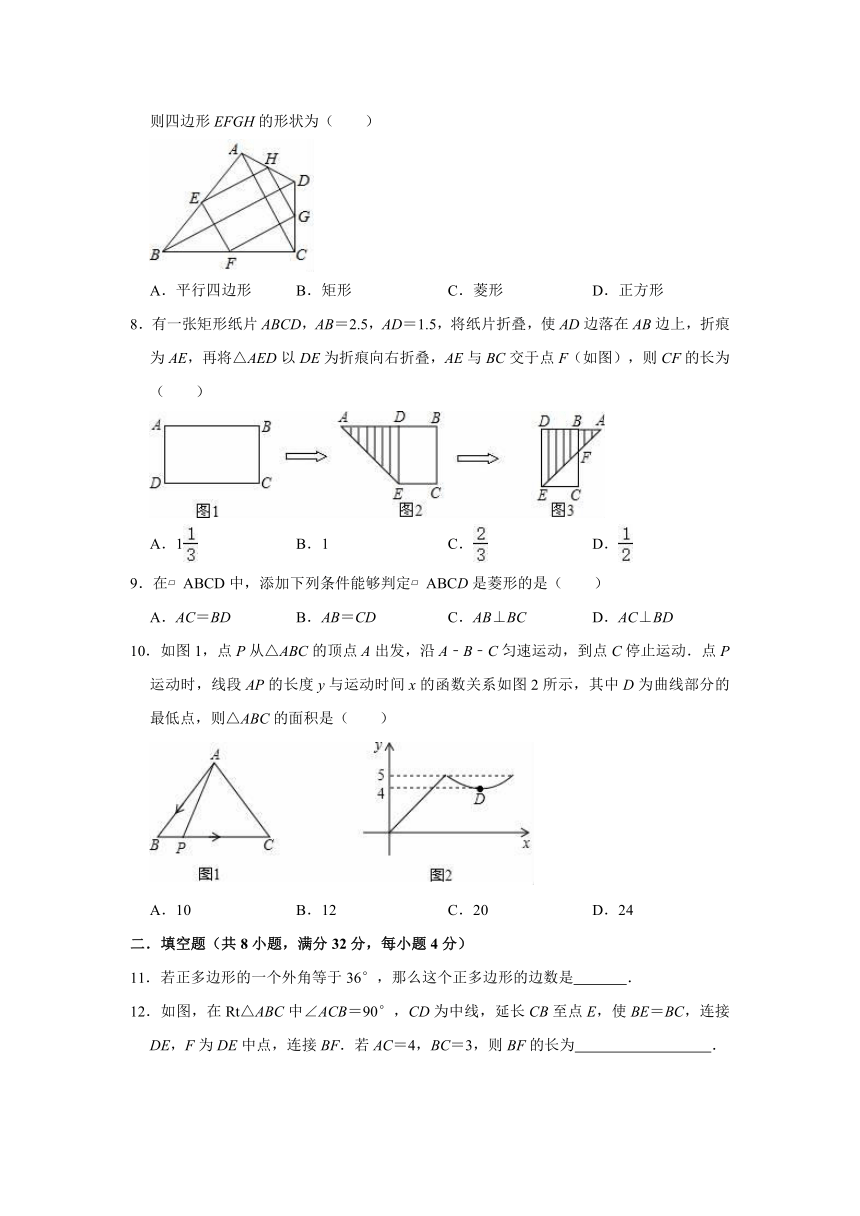
7.如图,点E,F,G,H分别是四边形ABCD边AB,BC,CD,DA的中点.若AC⊥BD,则四边形EFGH的形状为( )
A.平行四边形
B.矩形
C.菱形
D.正方形
8.有一张矩形纸片ABCD,AB=2.5,AD=1.5,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F(如图),则CF的长为( )
A.1
B.1
C.
D.
9.在?ABCD中,添加下列条件能够判定?ABCD是菱形的是( )
A.AC=BD
B.AB=CD
C.AB⊥BC
D.AC⊥BD
10.如图1,点P从△ABC的顶点A出发,沿A﹣B﹣C匀速运动,到点C停止运动.点P运动时,线段AP的长度y与运动时间x的函数关系如图2所示,其中D为曲线部分的最低点,则△ABC的面积是( )
A.10
B.12
C.20
D.24
二.填空题(共8小题,满分32分,每小题4分)
11.若正多边形的一个外角等于36°,那么这个正多边形的边数是
.
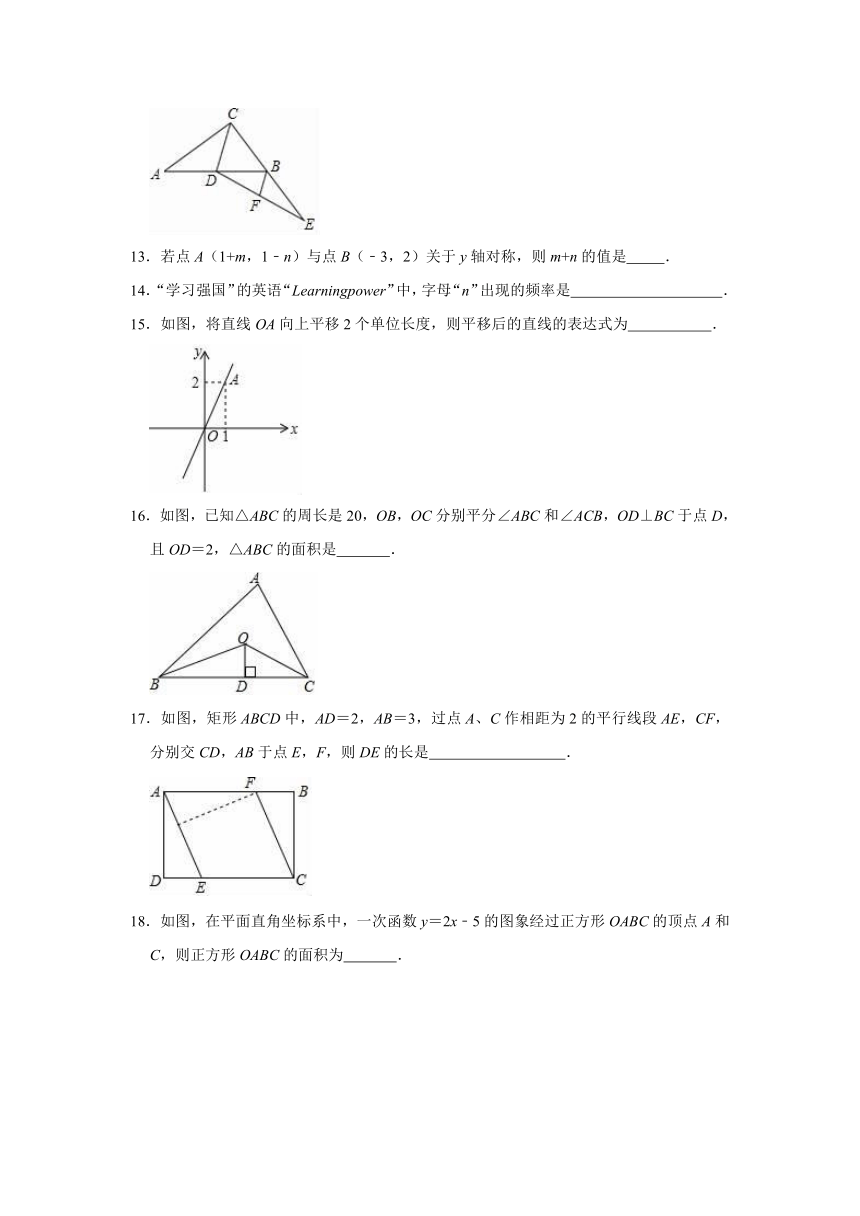
12.如图,在Rt△ABC中∠ACB=90°,CD为中线,延长CB至点E,使BE=BC,连接DE,F为DE中点,连接BF.若AC=4,BC=3,则BF的长为
.
13.若点A(1+m,1﹣n)与点B(﹣3,2)关于y轴对称,则m+n的值是
.
14.“学习强国”的英语“Learningpower”中,字母“n”出现的频率是
.
15.如图,将直线OA向上平移2个单位长度,则平移后的直线的表达式为
.
16.如图,已知△ABC的周长是20,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=2,△ABC的面积是
.
17.如图,矩形ABCD中,AD=2,AB=3,过点A、C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DE的长是
.
18.如图,在平面直角坐标系中,一次函数y=2x﹣5的图象经过正方形OABC的顶点A和C,则正方形OABC的面积为
.
三.解答题(共8小题,满分78分)
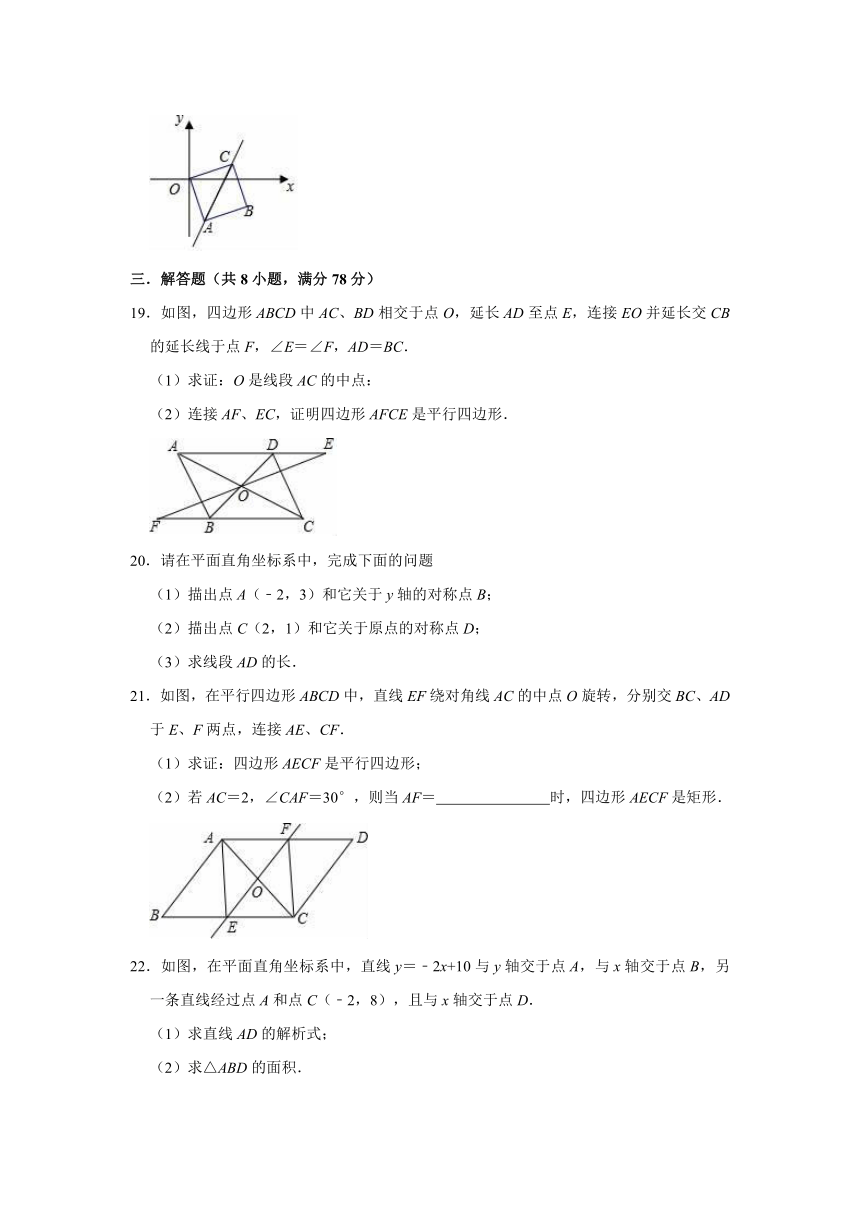
19.如图,四边形ABCD中AC、BD相交于点O,延长AD至点E,连接EO并延长交CB的延长线于点F,∠E=∠F,AD=BC.
(1)求证:O是线段AC的中点:
(2)连接AF、EC,证明四边形AFCE是平行四边形.
20.请在平面直角坐标系中,完成下面的问题
(1)描出点A(﹣2,3)和它关于y轴的对称点B;
(2)描出点C(2,1)和它关于原点的对称点D;
(3)求线段AD的长.
21.如图,在平行四边形ABCD中,直线EF绕对角线AC的中点O旋转,分别交BC、AD于E、F两点,连接AE、CF.
(1)求证:四边形AECF是平行四边形;
(2)若AC=2,∠CAF=30°,则当AF=
时,四边形AECF是矩形.
22.如图,在平面直角坐标系中,直线y=﹣2x+10与y轴交于点A,与x轴交于点B,另一条直线经过点A和点C(﹣2,8),且与x轴交于点D.
(1)求直线AD的解析式;
(2)求△ABD的面积.
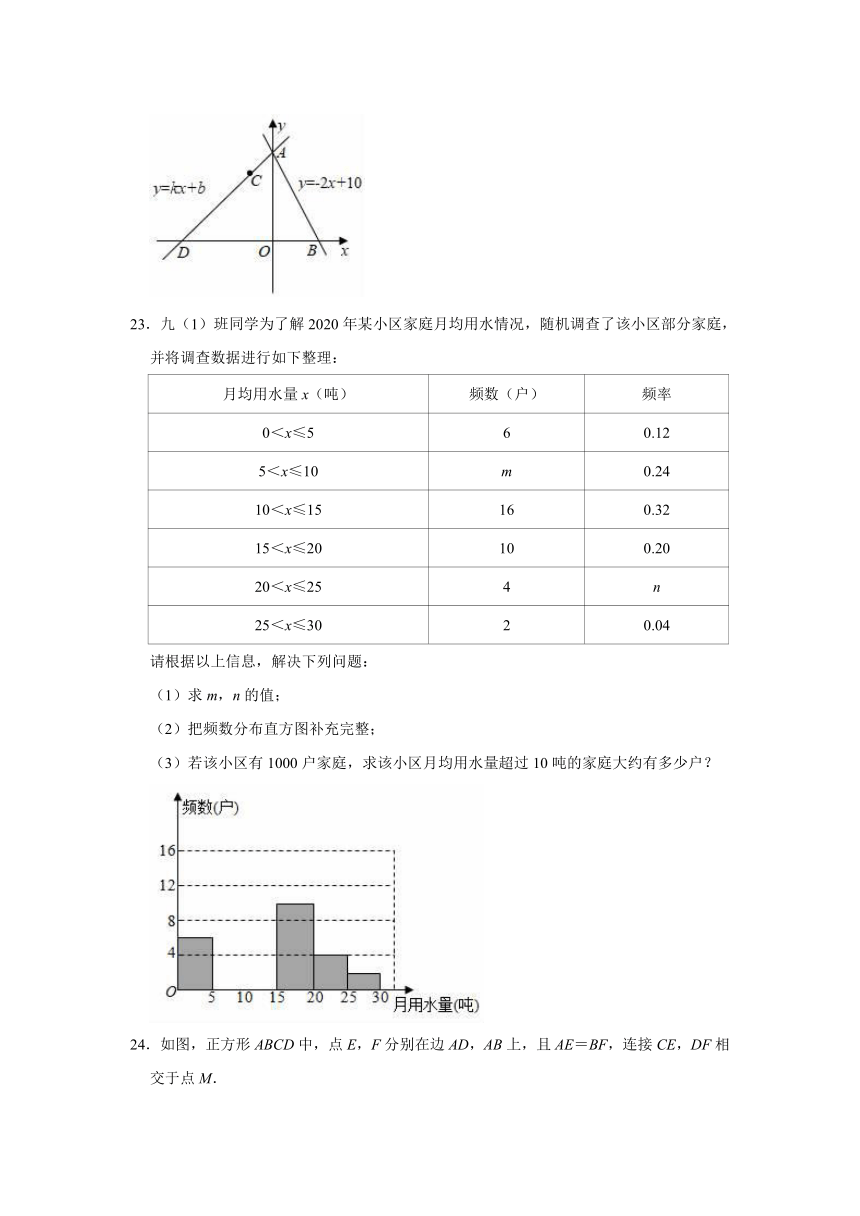
23.九(1)班同学为了解2020年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理:
月均用水量x(吨)
频数(户)
频率
0<x≤5
6
0.12
5<x≤10
m
0.24
10<x≤15
16
0.32
15<x≤20
10
0.20
20<x≤25
4
n
25<x≤30
2
0.04
请根据以上信息,解决下列问题:
(1)求m,n的值;
(2)把频数分布直方图补充完整;
(3)若该小区有1000户家庭,求该小区月均用水量超过10吨的家庭大约有多少户?
24.如图,正方形ABCD中,点E,F分别在边AD,AB上,且AE=BF,连接CE,DF相交于点M.
(1)当∠ADF=36°时,∠DCE=
°;
(2)判断CE,DF的位置关系,并证明.
25.甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地的距离y(千米)与时间x(时)之间的函数关系,请根据图象解答下列问题:
(1)轿车到达乙地时,求货车与甲地的距离;
(2)求线段CD对应的函数表达式;
(3)在轿车行进过程,轿车行驶多少时间,两车相距15千米.
26.如图,点E是矩形ABCD的边CB延长线上一点,点F是AE的中点.
(1)如图①,若点G,H分别是ED,BC的中点;
①判断FG和HC之间的关系,并说明理由;
②求证:∠DEH=∠FHE;
(2)如图②,若CE=AC,连接BF,DF.求证:BF⊥DF.
参考答案与试题解析
一.选择题(共10小题,满分40分,每小题4分)
1.解:A、12+()2=()2,故能构成直角三角形;
B、()2+()2=()2,故能构成直角三角形;
C、22+()2≠()2,故不能构成直角三角形;
D、12+()2=22,故能构成直角三角形.
故选:C.
2.解:A、不是中心对称图形,故本选项不符合题意;
B、不是中心对称图形,故本选项不符合题意;
C、是中心对称图形,故本选项符合题意;
D、不是中心对称图形,故本选项不符合题意.
故选:C.
3.解:设该一次函数为y=kx+b(k≠0),
由于该一次函数的图象是y随x值增大而增大,
所以k>0.
观察选项,只有选项A符合题意.
故选:A.
4.解:优胜者的频率是18÷(1+19+22+18)=0.3=30%,
故选:B.
5.解:∵点P(a﹣3,a+2)在x轴上,
∴a+2=0,
∴a=﹣2.
故选:A.
6.解:如图,取AD的中点M,连接CM、AG、AC,作AN⊥BC于N.
∵四边形ABCD是平行四边形,∠BCD=120°,
∴∠D=180°﹣∠BCD=60°,AB=CD=2,
∵AM=DM=DC=2,
∴△CDM是等边三角形,
∴∠DMC=∠MCD=60°,CM=DM=AM,
∴∠MAC=∠MCA=30°,
∴∠ACD=90°,
∴AC=2,
在Rt△ACN中,∵AC=2,∠ACN=∠DAC=30°,
∴AN=AC=,
∵AE=EH,GF=FH,
∴EF=AG,
易知AG的最大值为AC的长,最小值为AN的长,
∴AG的最大值为2,最小值为,
∴EF的最大值为,最小值为,
∴EF的最大值与最小值的差为.
故选:C.
7.解:∵点E、F、G、H分别为四边形ABCD的边AB、BC、CD、DA的中点,
∴EF是△ABC的中位线,GH是△ACD的中位线,FG是△BCD的中位线,EH是△ABD的中位线,
∴EF∥AC,GH∥AC,FG∥BD,EH∥BD,
∴EF∥GH,FG∥EH,
∴四边形EFGH是平行四边形,
又∵AC⊥BD,
∴EF⊥FG,
∴∠EFG=90°,
∴四边形EFGH是矩形;
故选:B.
8.解:如图2,根据题意得:BD=AB﹣AD=2.5﹣1.5=1,
如图3,AB=AD﹣BD=1.5﹣1=0.5,
∵BC∥DE,
∴△ABF∽△ADE,
∴=,
即,
∴BF=0.5,
∴CF=BC﹣BF=1.5﹣0.5=1.
故选:B.
9.解:∵四边形ABCD是平行四边形,
∵AC⊥BD,
∴平行四边形ABCD是菱形,
故选:D.
10.解:根据图象可知,点P在AB上运动时,此时AP不断增大,
由图象可知:点P从A向B运动时,AP的最大值为5,即AB=5,
点P从B向C运动时,AP的最小值为4,
即BC边上的高为4,
∴当AP⊥BC,AP=4,
此时,由勾股定理可知:BP=3,
由于图象的曲线部分是轴对称图形,
∴PC=3,
∴BC=6,
∴△ABC的面积为:×4×6=12,
故选:B.
二.填空题(共8小题,满分32分,每小题4分)
11.解:正多边形的一个外角等于36°,且外角和为360°,
则这个正多边形的边数是:360°÷36°=10.
故答案为:10.
12.解:∵在Rt△ABC中,∠ACB=90°,AC=4,BC=3,
∴AB===5,
又∵CD为中线,
∴CD=AB=.
∵F为DE中点,BE=BC,即点B是EC的中点,
∴BF是△CDE的中位线,则BF=CD=.
故答案为:.
13.解:∵点A(1+m,1﹣n)与点B(﹣3,2)关于y轴对称,
∴1+m=3、1﹣n=2,
解得:m=2、n=﹣1,
所以m+n=2﹣1=1,
故答案为:1.
14.解:∵“学习强国”的英语“Learningpower”中,一共有13个字母,n有2个,
∴字母“n”出现的频率是:.
故答案为:.
15.解:设直线OA的解析式为:y=kx,
把(1,2)代入,得k=2,
则直线OA解析式是:y=2x.
将其上平移2个单位长度,则平移后的直线的表达式为:y=2x+2.
故答案是:y=2x+2.
16.解:如图,连接OA,过O作OE⊥AB于E,OF⊥AC于F,
∵OB、OC分别平分∠ABC和∠ACB,
∴OE=OF=OD=2,
∵△ABC的周长是20,OD⊥BC于D,且OD=2,
∴S△ABC=×AB×OE+×BC×OD+×AC×OF
=×(AB+BC+AC)×2
=×20×2
=20,
故答案为:20.
17.解:∵四边形ABCD是矩形,
∴AB∥CD,
∴∠FAH=∠AED,
∵∠ADE=∠AHF=∠DAF=90°,AD=2,FH=2,
∴AD=FH,
∴△ADE≌△FAH(AAS),
∴AF=AE,
∵AE∥CF,AF∥EC,
∴四边形AECF是平行四边形,
∵AF=AE,
∴四边形AECF是菱形,
设DE=x,则BF=x,CE=CF=3﹣x,
在Rt△BCF中,(3﹣x)2=x2+22,
解得x=;
故答案为:.
18.解:过点C作CM⊥x轴于点M,过点A作AN⊥y轴于点N,
∵∠COM+∠MOA=∠MOA+∠NOA=90°,
∴∠NOA=∠COM,
又因为OA=OC,
∴Rt△OCM≌Rt△OAN(ASA),
∴OM=ON,CM=AN,
设点C
(a,b),
∵点A在函数y=2x﹣5的图象上,
∴b=2a﹣5,
∴CM=AN=2a﹣5,OM=ON=a,
∴A(2a﹣5,﹣a),
∴﹣a=2(2a﹣5)﹣5,
∴a=3,
∴A(1,﹣3),
在直角三角形OCM中,由勾股定理可求得OA=,
∴正方形OABC的面积是10,
故答案为10.
三.解答题(共8小题,满分78分)
19.证明:(1)∵∠E=∠F,
∴AD∥BC,
∵AD=BC,
∴四边形ABCD是平行四边形,
∴AC,BD互相平分;
即O是线段AC的中点.
(2)∵AD∥BC,
∴∠EAC=∠FCA,
在△OAE和△OCF中,
,
∴△OAE≌△OCF(ASA).
∴OE=OF,
∴四边形AFCE是平行四边形.
20.解:(1)如图,点B为所作;
(2)如图,点D为所作;
(3)因为A(﹣2,3),D(﹣2,﹣1),
线段AD的长=3﹣(﹣1)=4.
21.证明:(1)在平行四边形ABCD中,AD∥BC,
∴∠CAF=∠ACE,
∵点O是平行四边形ABCD对角线的中点,
∴OA=OC,
在△AOF和△COE中,
∵,
∴△AOF≌△COE(ASA),
∴AF=CE,
∵AF∥CE,
∴四边形AECF是平行四边形;
(2)∵四边形AECF是矩形,
∴∠AFC=90°,
在Rt△ACF中,∠CAF=30°,AC=2,
∴CF=1,AF=.
故答案为:.
22.解:(1)∵直线y=﹣2x+10与y轴交于点A,
∴A(0,10).
设直线AD的解析式为y=kx+b,
∵直线AD过A(0,10),C(﹣2,8),
∴,解得,
∴直线AD的解析式为y=x+10;
(2)∵直线y=﹣2x+10与x轴交于点B,
∴B(5,0),
∵直线AD与x轴交于点D,
∴D(﹣10,0),
∴BD=15,
∵A(0,10),
∴△ABD的面积=BD?OA=×15×10=75.
23.解:(1)6÷0.12=50(户),
m=50×0.24=12(户),
n=4÷50=0.08,
(2)补全频数分布直方图;
(3)1000×(0.32+0.20+0.08+0.04)=640(户)
答:该小区月均用水量超过10吨的家庭大约有640户.
24.解:(1)∵四边形ABCD是正方形,
∴CD=AD=AB,∠CDE=∠DAF=90°,
又∵AE=BF,
∴DE=AF,
在△CDE和△DAF中,
,
∴△CDE≌△DAF(SAS),
∴∠DCE=∠ADF,
∵∠ADF=36°,
∴∠DCE=36°,
故答案为:36;
(2)CE,DF的位置关系互相垂直,
证明:由(1)知∠DCE=∠ADF,
∵∠ADF+∠MDC=∠CDE=90°,
∴∠DCE+∠MDC=90°,
∴∠DMC=90°,
∴CE⊥DF,
即CE,DF的位置关系互相垂直.
25.解:(1)由图象可得,
货车的速度为300÷5=60(千米/小时),
则轿车到达乙地时,货车与甲地的距离是60×4.5=270(千米),
即轿车到达乙地时,货车与甲地的距离是270千米;
(2)设线段CD对应的函数表达式是y=kx+b,
∵点C(2.5,80),点D(4.5,300),
∴,
解得,
即线段CD对应的函数表达式是y=110x﹣195(2.5≤x≤4.5);
(3)当x=2.5时,两车之间的距离为:60×2.5﹣80=70,
∵70>15,
∴在轿车行进过程,两车相距15千米时间是在2.5~4.5之间,
由图象可得,线段OA对应的函数解析式为y=60x,
则|60x﹣(110x﹣195)|=15,
解得x1=3.6,x2=4.2,
∵轿车比货车晚出发1.5小时,3.6﹣1.5=2.1(小时),4.2﹣1.5=2.7(小时),
∴在轿车行进过程,轿车行驶2.1小时或2.7小时,两车相距15千米,
答:在轿车行进过程,轿车行驶2.1小时或2.7小时,两车相距15千米.
26.(1)①解:判断:FG=HC,FG∥HC;理由如下:
∵点F,G分别是AE,DE的中点,
∴FG是△AED的中位线,
∴FG=AD,FG∥AD,
∵H是BC的中点,
∴CH=BC,
∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,
∴FG=HC,FG∥HC;
②证明:∵四边形ABCD是矩形,
∴∠BCD=90°
∵G是DE的中点,
∴CG=DE=GE,
∴∠GEH=∠GCE,
∵FG=HC,FG∥HC,
∴四边形FHCG是平行四边形,
∴FH∥GC,
∴∠FHE=∠GCE,
∴∠GEH=∠FHE,即∠DEH=∠FHE;
(2)证明:连接FC,如图②所示:
∵四边形ABCD是矩形,
∴∠BAD=∠ABC=90°,AD=BC,
∴∠ABE=90°
∵F是AE的中点,
∴BF=AE=AF,
∴∠FBA=∠FAB,
∴∠FBC=∠FAD,
在△BFC和△AFD中,,
∴△BFC≌△AFD(SAS)
∴∠BFC=∠AFD
∵CE=AC,F是AE的中点,
∴CF⊥AE,
∴∠CFD+∠AFD=90°,
∴∠CFD+∠BFC=90°,
∴BF⊥DF.
一.选择题(共10小题,满分40分,每小题4分)
1.下列各组线段中,不能构成直角三角形的是( )
A.1、、
B.、、
C.2、、
D.1、2、
2.下列图形中,是中心对称图形的是( )
A.
B.
C.
D.
3.下列一次函数中,y随x值增大而增大的是( )
A.y=8x﹣7
B.y=6﹣5x
C.y=﹣8﹣x
D.y=(﹣)x
4.社会主义核心价值观知识竞赛成绩结果统计如下表:成绩在91~100分的为优胜者,则优胜者的频率是( )
分段数(分)
61~70
71~80
81~90
91~100
人数(人)
1
19
22
18
A.35%
B.30%
C.20%
D.10%
5.已知点P(a﹣3,a+2)在x轴上,则a=( )
A.﹣2
B.3
C.﹣5
D.5
6.如图,在平行四边形ABCD中,∠C=120°,AD=4,AB=2,点H、G分别是边CD、BC上的动点.连接AH、HG,点E为AH的中点,点F为GH的中点,连接EF.则EF的最大值与最小值的差为( )
A.1
B.﹣1
C.
D.2﹣
7.如图,点E,F,G,H分别是四边形ABCD边AB,BC,CD,DA的中点.若AC⊥BD,则四边形EFGH的形状为( )
A.平行四边形
B.矩形
C.菱形
D.正方形
8.有一张矩形纸片ABCD,AB=2.5,AD=1.5,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F(如图),则CF的长为( )
A.1
B.1
C.
D.
9.在?ABCD中,添加下列条件能够判定?ABCD是菱形的是( )
A.AC=BD
B.AB=CD
C.AB⊥BC
D.AC⊥BD
10.如图1,点P从△ABC的顶点A出发,沿A﹣B﹣C匀速运动,到点C停止运动.点P运动时,线段AP的长度y与运动时间x的函数关系如图2所示,其中D为曲线部分的最低点,则△ABC的面积是( )
A.10
B.12
C.20
D.24
二.填空题(共8小题,满分32分,每小题4分)
11.若正多边形的一个外角等于36°,那么这个正多边形的边数是
.
12.如图,在Rt△ABC中∠ACB=90°,CD为中线,延长CB至点E,使BE=BC,连接DE,F为DE中点,连接BF.若AC=4,BC=3,则BF的长为
.
13.若点A(1+m,1﹣n)与点B(﹣3,2)关于y轴对称,则m+n的值是
.
14.“学习强国”的英语“Learningpower”中,字母“n”出现的频率是
.
15.如图,将直线OA向上平移2个单位长度,则平移后的直线的表达式为
.
16.如图,已知△ABC的周长是20,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=2,△ABC的面积是
.
17.如图,矩形ABCD中,AD=2,AB=3,过点A、C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DE的长是
.
18.如图,在平面直角坐标系中,一次函数y=2x﹣5的图象经过正方形OABC的顶点A和C,则正方形OABC的面积为
.
三.解答题(共8小题,满分78分)
19.如图,四边形ABCD中AC、BD相交于点O,延长AD至点E,连接EO并延长交CB的延长线于点F,∠E=∠F,AD=BC.
(1)求证:O是线段AC的中点:
(2)连接AF、EC,证明四边形AFCE是平行四边形.
20.请在平面直角坐标系中,完成下面的问题
(1)描出点A(﹣2,3)和它关于y轴的对称点B;
(2)描出点C(2,1)和它关于原点的对称点D;
(3)求线段AD的长.
21.如图,在平行四边形ABCD中,直线EF绕对角线AC的中点O旋转,分别交BC、AD于E、F两点,连接AE、CF.
(1)求证:四边形AECF是平行四边形;
(2)若AC=2,∠CAF=30°,则当AF=
时,四边形AECF是矩形.
22.如图,在平面直角坐标系中,直线y=﹣2x+10与y轴交于点A,与x轴交于点B,另一条直线经过点A和点C(﹣2,8),且与x轴交于点D.
(1)求直线AD的解析式;
(2)求△ABD的面积.
23.九(1)班同学为了解2020年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理:
月均用水量x(吨)
频数(户)
频率
0<x≤5
6
0.12
5<x≤10
m
0.24
10<x≤15
16
0.32
15<x≤20
10
0.20
20<x≤25
4
n
25<x≤30
2
0.04
请根据以上信息,解决下列问题:
(1)求m,n的值;
(2)把频数分布直方图补充完整;
(3)若该小区有1000户家庭,求该小区月均用水量超过10吨的家庭大约有多少户?
24.如图,正方形ABCD中,点E,F分别在边AD,AB上,且AE=BF,连接CE,DF相交于点M.
(1)当∠ADF=36°时,∠DCE=
°;
(2)判断CE,DF的位置关系,并证明.
25.甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地的距离y(千米)与时间x(时)之间的函数关系,请根据图象解答下列问题:
(1)轿车到达乙地时,求货车与甲地的距离;
(2)求线段CD对应的函数表达式;
(3)在轿车行进过程,轿车行驶多少时间,两车相距15千米.
26.如图,点E是矩形ABCD的边CB延长线上一点,点F是AE的中点.
(1)如图①,若点G,H分别是ED,BC的中点;
①判断FG和HC之间的关系,并说明理由;
②求证:∠DEH=∠FHE;
(2)如图②,若CE=AC,连接BF,DF.求证:BF⊥DF.
参考答案与试题解析
一.选择题(共10小题,满分40分,每小题4分)
1.解:A、12+()2=()2,故能构成直角三角形;
B、()2+()2=()2,故能构成直角三角形;
C、22+()2≠()2,故不能构成直角三角形;
D、12+()2=22,故能构成直角三角形.
故选:C.
2.解:A、不是中心对称图形,故本选项不符合题意;
B、不是中心对称图形,故本选项不符合题意;
C、是中心对称图形,故本选项符合题意;
D、不是中心对称图形,故本选项不符合题意.
故选:C.
3.解:设该一次函数为y=kx+b(k≠0),
由于该一次函数的图象是y随x值增大而增大,
所以k>0.
观察选项,只有选项A符合题意.
故选:A.
4.解:优胜者的频率是18÷(1+19+22+18)=0.3=30%,
故选:B.
5.解:∵点P(a﹣3,a+2)在x轴上,
∴a+2=0,
∴a=﹣2.
故选:A.
6.解:如图,取AD的中点M,连接CM、AG、AC,作AN⊥BC于N.
∵四边形ABCD是平行四边形,∠BCD=120°,
∴∠D=180°﹣∠BCD=60°,AB=CD=2,
∵AM=DM=DC=2,
∴△CDM是等边三角形,
∴∠DMC=∠MCD=60°,CM=DM=AM,
∴∠MAC=∠MCA=30°,
∴∠ACD=90°,
∴AC=2,
在Rt△ACN中,∵AC=2,∠ACN=∠DAC=30°,
∴AN=AC=,
∵AE=EH,GF=FH,
∴EF=AG,
易知AG的最大值为AC的长,最小值为AN的长,
∴AG的最大值为2,最小值为,
∴EF的最大值为,最小值为,
∴EF的最大值与最小值的差为.
故选:C.
7.解:∵点E、F、G、H分别为四边形ABCD的边AB、BC、CD、DA的中点,
∴EF是△ABC的中位线,GH是△ACD的中位线,FG是△BCD的中位线,EH是△ABD的中位线,
∴EF∥AC,GH∥AC,FG∥BD,EH∥BD,
∴EF∥GH,FG∥EH,
∴四边形EFGH是平行四边形,
又∵AC⊥BD,
∴EF⊥FG,
∴∠EFG=90°,
∴四边形EFGH是矩形;
故选:B.
8.解:如图2,根据题意得:BD=AB﹣AD=2.5﹣1.5=1,
如图3,AB=AD﹣BD=1.5﹣1=0.5,
∵BC∥DE,
∴△ABF∽△ADE,
∴=,
即,
∴BF=0.5,
∴CF=BC﹣BF=1.5﹣0.5=1.
故选:B.
9.解:∵四边形ABCD是平行四边形,
∵AC⊥BD,
∴平行四边形ABCD是菱形,
故选:D.
10.解:根据图象可知,点P在AB上运动时,此时AP不断增大,
由图象可知:点P从A向B运动时,AP的最大值为5,即AB=5,
点P从B向C运动时,AP的最小值为4,
即BC边上的高为4,
∴当AP⊥BC,AP=4,
此时,由勾股定理可知:BP=3,
由于图象的曲线部分是轴对称图形,
∴PC=3,
∴BC=6,
∴△ABC的面积为:×4×6=12,
故选:B.
二.填空题(共8小题,满分32分,每小题4分)
11.解:正多边形的一个外角等于36°,且外角和为360°,
则这个正多边形的边数是:360°÷36°=10.
故答案为:10.
12.解:∵在Rt△ABC中,∠ACB=90°,AC=4,BC=3,
∴AB===5,
又∵CD为中线,
∴CD=AB=.
∵F为DE中点,BE=BC,即点B是EC的中点,
∴BF是△CDE的中位线,则BF=CD=.
故答案为:.
13.解:∵点A(1+m,1﹣n)与点B(﹣3,2)关于y轴对称,
∴1+m=3、1﹣n=2,
解得:m=2、n=﹣1,
所以m+n=2﹣1=1,
故答案为:1.
14.解:∵“学习强国”的英语“Learningpower”中,一共有13个字母,n有2个,
∴字母“n”出现的频率是:.
故答案为:.
15.解:设直线OA的解析式为:y=kx,
把(1,2)代入,得k=2,
则直线OA解析式是:y=2x.
将其上平移2个单位长度,则平移后的直线的表达式为:y=2x+2.
故答案是:y=2x+2.
16.解:如图,连接OA,过O作OE⊥AB于E,OF⊥AC于F,
∵OB、OC分别平分∠ABC和∠ACB,
∴OE=OF=OD=2,
∵△ABC的周长是20,OD⊥BC于D,且OD=2,
∴S△ABC=×AB×OE+×BC×OD+×AC×OF
=×(AB+BC+AC)×2
=×20×2
=20,
故答案为:20.
17.解:∵四边形ABCD是矩形,
∴AB∥CD,
∴∠FAH=∠AED,
∵∠ADE=∠AHF=∠DAF=90°,AD=2,FH=2,
∴AD=FH,
∴△ADE≌△FAH(AAS),
∴AF=AE,
∵AE∥CF,AF∥EC,
∴四边形AECF是平行四边形,
∵AF=AE,
∴四边形AECF是菱形,
设DE=x,则BF=x,CE=CF=3﹣x,
在Rt△BCF中,(3﹣x)2=x2+22,
解得x=;
故答案为:.
18.解:过点C作CM⊥x轴于点M,过点A作AN⊥y轴于点N,
∵∠COM+∠MOA=∠MOA+∠NOA=90°,
∴∠NOA=∠COM,
又因为OA=OC,
∴Rt△OCM≌Rt△OAN(ASA),
∴OM=ON,CM=AN,
设点C
(a,b),
∵点A在函数y=2x﹣5的图象上,
∴b=2a﹣5,
∴CM=AN=2a﹣5,OM=ON=a,
∴A(2a﹣5,﹣a),
∴﹣a=2(2a﹣5)﹣5,
∴a=3,
∴A(1,﹣3),
在直角三角形OCM中,由勾股定理可求得OA=,
∴正方形OABC的面积是10,
故答案为10.
三.解答题(共8小题,满分78分)
19.证明:(1)∵∠E=∠F,
∴AD∥BC,
∵AD=BC,
∴四边形ABCD是平行四边形,
∴AC,BD互相平分;
即O是线段AC的中点.
(2)∵AD∥BC,
∴∠EAC=∠FCA,
在△OAE和△OCF中,
,
∴△OAE≌△OCF(ASA).
∴OE=OF,
∴四边形AFCE是平行四边形.
20.解:(1)如图,点B为所作;
(2)如图,点D为所作;
(3)因为A(﹣2,3),D(﹣2,﹣1),
线段AD的长=3﹣(﹣1)=4.
21.证明:(1)在平行四边形ABCD中,AD∥BC,
∴∠CAF=∠ACE,
∵点O是平行四边形ABCD对角线的中点,
∴OA=OC,
在△AOF和△COE中,
∵,
∴△AOF≌△COE(ASA),
∴AF=CE,
∵AF∥CE,
∴四边形AECF是平行四边形;
(2)∵四边形AECF是矩形,
∴∠AFC=90°,
在Rt△ACF中,∠CAF=30°,AC=2,
∴CF=1,AF=.
故答案为:.
22.解:(1)∵直线y=﹣2x+10与y轴交于点A,
∴A(0,10).
设直线AD的解析式为y=kx+b,
∵直线AD过A(0,10),C(﹣2,8),
∴,解得,
∴直线AD的解析式为y=x+10;
(2)∵直线y=﹣2x+10与x轴交于点B,
∴B(5,0),
∵直线AD与x轴交于点D,
∴D(﹣10,0),
∴BD=15,
∵A(0,10),
∴△ABD的面积=BD?OA=×15×10=75.
23.解:(1)6÷0.12=50(户),
m=50×0.24=12(户),
n=4÷50=0.08,
(2)补全频数分布直方图;
(3)1000×(0.32+0.20+0.08+0.04)=640(户)
答:该小区月均用水量超过10吨的家庭大约有640户.
24.解:(1)∵四边形ABCD是正方形,
∴CD=AD=AB,∠CDE=∠DAF=90°,
又∵AE=BF,
∴DE=AF,
在△CDE和△DAF中,
,
∴△CDE≌△DAF(SAS),
∴∠DCE=∠ADF,
∵∠ADF=36°,
∴∠DCE=36°,
故答案为:36;
(2)CE,DF的位置关系互相垂直,
证明:由(1)知∠DCE=∠ADF,
∵∠ADF+∠MDC=∠CDE=90°,
∴∠DCE+∠MDC=90°,
∴∠DMC=90°,
∴CE⊥DF,
即CE,DF的位置关系互相垂直.
25.解:(1)由图象可得,
货车的速度为300÷5=60(千米/小时),
则轿车到达乙地时,货车与甲地的距离是60×4.5=270(千米),
即轿车到达乙地时,货车与甲地的距离是270千米;
(2)设线段CD对应的函数表达式是y=kx+b,
∵点C(2.5,80),点D(4.5,300),
∴,
解得,
即线段CD对应的函数表达式是y=110x﹣195(2.5≤x≤4.5);
(3)当x=2.5时,两车之间的距离为:60×2.5﹣80=70,
∵70>15,
∴在轿车行进过程,两车相距15千米时间是在2.5~4.5之间,
由图象可得,线段OA对应的函数解析式为y=60x,
则|60x﹣(110x﹣195)|=15,
解得x1=3.6,x2=4.2,
∵轿车比货车晚出发1.5小时,3.6﹣1.5=2.1(小时),4.2﹣1.5=2.7(小时),
∴在轿车行进过程,轿车行驶2.1小时或2.7小时,两车相距15千米,
答:在轿车行进过程,轿车行驶2.1小时或2.7小时,两车相距15千米.
26.(1)①解:判断:FG=HC,FG∥HC;理由如下:
∵点F,G分别是AE,DE的中点,
∴FG是△AED的中位线,
∴FG=AD,FG∥AD,
∵H是BC的中点,
∴CH=BC,
∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,
∴FG=HC,FG∥HC;
②证明:∵四边形ABCD是矩形,
∴∠BCD=90°
∵G是DE的中点,
∴CG=DE=GE,
∴∠GEH=∠GCE,
∵FG=HC,FG∥HC,
∴四边形FHCG是平行四边形,
∴FH∥GC,
∴∠FHE=∠GCE,
∴∠GEH=∠FHE,即∠DEH=∠FHE;
(2)证明:连接FC,如图②所示:
∵四边形ABCD是矩形,
∴∠BAD=∠ABC=90°,AD=BC,
∴∠ABE=90°
∵F是AE的中点,
∴BF=AE=AF,
∴∠FBA=∠FAB,
∴∠FBC=∠FAD,
在△BFC和△AFD中,,
∴△BFC≌△AFD(SAS)
∴∠BFC=∠AFD
∵CE=AC,F是AE的中点,
∴CF⊥AE,
∴∠CFD+∠AFD=90°,
∴∠CFD+∠BFC=90°,
∴BF⊥DF.
同课章节目录
