数学人教A版(2019)必修第二册10.3 频率与概率(共30张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册10.3 频率与概率(共30张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 742.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 00:00:00 | ||
图片预览









文档简介
(共30张PPT)
10.3
频率与概率
1、在问题情景中了解频率与概率的关系
2、理解频率与概率的关系,明确事件A发生的概率fn(A)与事件A发生的概率P(A)的区别与联系
3、了解蒙特卡洛方法,通过实例理解其步骤
学习目标
一、复习回顾
抛掷一枚质地均匀的硬币,“正面朝上”的概率为.
(样本点等可能)
(样本点不是等可能)
抛掷一枚图钉,“针尖朝上”的概率为多少?
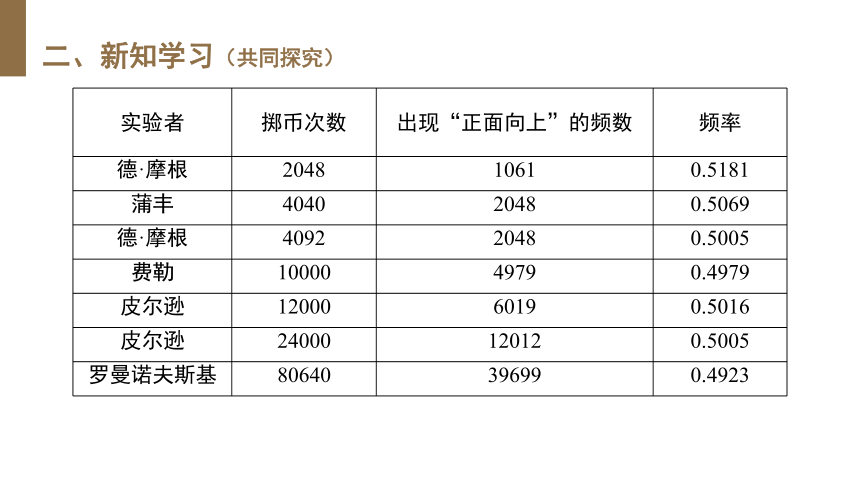
实验者
掷币次数
出现“正面向上”的频数
频率
德·摩根
2048
1061
0.5181
蒲丰
4040
2048
0.5069
德·摩根
4092
2048
0.5005
费勒
10000
4979
0.4979
皮尔逊
12000
6019
0.5016
皮尔逊
24000
12012
0.5005
罗曼诺夫斯基
80640
39699
0.4923
二、新知学习(共同探究)
在重复试验中,频率的大小是否就决定了概率的大小呢?
频率与概率之间到底是一种怎样的关系呢?
二、新知学习(思考)
二、新知学习(共同探究)
重复做同时抛掷两枚质地均匀的硬币实验,设事件A=“一个正面朝上,一个反面朝上”,统计A出现的次数并计算频率,再与其概率进行比较,你能发现什么规律?
分析:把硬币正面朝上记为1,反面朝上记为0,
则这个试验的样本空间Ω=
,所以
二、新知学习(共同探究)
抛掷两枚质地均匀的硬币的试验:
(1)参与人员:42名高一学生;
(2)注意事项:每位同学都在相同的条件下同时抛掷两枚质地均匀的硬币.
二、新知学习(共同探究)
分步试验
第一步:每人重复做20次试验,记录事件A发生的次数,计算频率;
第三步:各组统计事件A发生的次数,计算事件A发生频率,然后汇总数据.
第二步:每7名同学为一组,相互比较试验结果,同时思考:每组中7名同学的结果一样吗?为什么会出现这样的情况?
二、新知学习(共同探究)
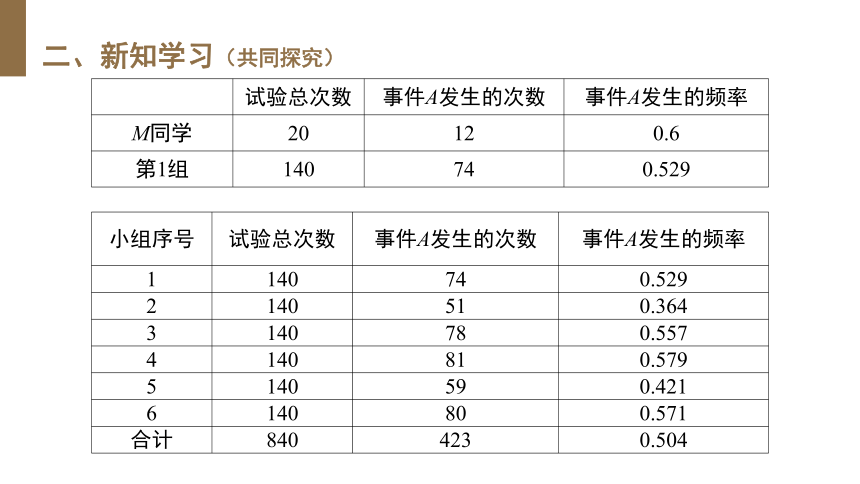
试验总次数
事件A发生的次数
事件A发生的频率
M同学
20
12
0.6
第1组
140
74
0.529
小组序号
试验总次数
事件A发生的次数
事件A发生的频率
1
140
74
0.529
2
140
51
0.364
3
140
78
0.557
4
140
81
0.579
5
140
59
0.421
6
140
80
0.571
合计
840
423
0.504
二、新知学习(思考)
(1)为什么各小组的试验结果不一样?
(2)随着试验次数的增加,事件A发生的频率有什么变化规律?
二、新知学习(共同探究)
试验总次数
事件A发生的次数
事件A发生的频率
M同学
20
12
0.6
第1组
140
74
0.529
小组序号
试验总次数
事件A发生的次数
事件A发生的频率
1
140
74
0.529
2
140
51
0.364
3
140
78
0.557
4
140
81
0.579
5
140
59
0.421
6
140
80
0.571
合计
840
423
0.504
二、新知学习(共同探究)
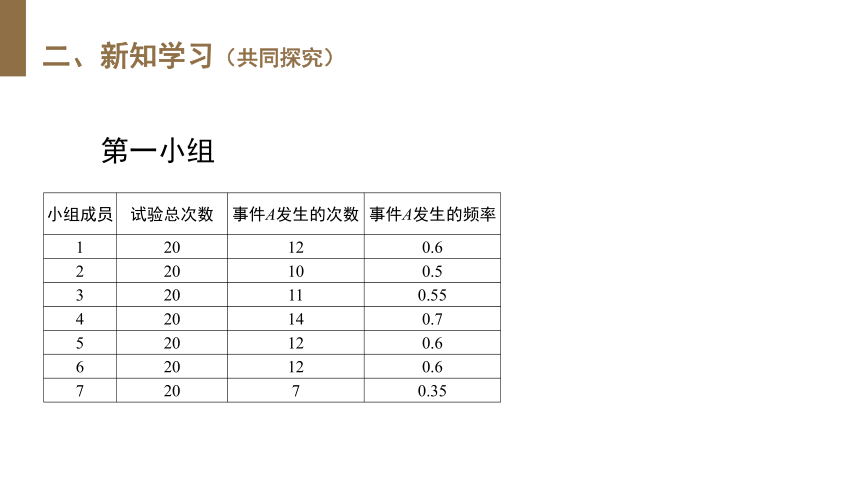
第一小组
小组成员
试验总次数
事件A发生的次数
事件A发生的频率
1
20
12
0.6
2
20
10
0.5
3
20
11
0.55
4
20
14
0.7
5
20
12
0.6
6
20
12
0.6
7
20
7
0.35
二、新知学习(共同探究)
第一小组
小组成员
试验总次数
事件A发生的次数
事件A发生的频率
1
20
12
0.6
2
20
10
0.5
3
20
11
0.55
4
20
14
0.7
5
20
12
0.6
6
20
12
0.6
7
20
7
0.35
二、新知学习(共同探究)
小组序号
试验总次数
事件A发生的次数
事件A发生的频率
1
140
74
0.529
2
140
51
0.364
3
140
78
0.557
4
140
81
0.579
5
140
59
0.421
6
140
80
0.571
合计
840
423
0.504
二、新知学习(共同探究)
小组序号
试验总次数
事件A发生的次数
事件A发生的频率
1
140
74
0.529
2
140
51
0.364
3
140
78
0.557
4
140
81
0.579
5
140
59
0.421
6
140
80
0.571
合计
840
423
0.504
二、新知学习(共同探究)
0.7-0.35=0.35
0.579-0.364=0.215
二、新知学习(共同探究)
小组序号
试验总次数
事件A发生的次数
事件A发生的频率
1
140
74
0.529
2
140
51
0.364
3
140
78
0.557
4
140
81
0.579
5
140
59
0.421
6
140
80
0.571
合计
840
423
0.504
试验次数为840次时,事件A发生的频率为0.504.
P(A)=0.5
二、新知学习(共同探究)
小组序号
试验总次数
事件A发生的次数
事件A发生的频率
1
140
74
0.529
2
140
51
0.364
3
140
78
0.557
4
140
81
0.579
5
140
59
0.421
6
140
80
0.571
合计
840
423
0.504
掷币次数
频率
2048
0.5181
4040
0.5069
4092
0.5005
10000
0.4979
12000
0.5016
24000
0.5005
80640
0.4923
0.504-0.
5=0.004
0.5181-0.
5=0.0181
二、新知学习(共同探究)
小组序号
试验总次数
事件A发生的次数
事件A发生的频率
1
140
74
0.529
2
140
51
0.364
3
140
78
0.557
4
140
81
0.579
5
140
59
0.421
6
140
80
0.571
合计
840
423
0.504
掷币次数
频率
2048
0.5181
4040
0.5069
4092
0.5005
10000
0.4979
12000
0.5016
24000
0.5005
80640
0.4923
只有1个:0.529
全部满足
事件A发生的频率记为
∣fn(A)-0.5∣≤0.05
二、新知学习(总结)
当试验次数较少时,用频率估计概率误差较小的可能性较小;
当试验次数足够多时,用频率估计概率误差较小的可能性大.
随着试验次数n的增大,频率偏离概率的幅度会缩小,即事件A发生的频率fn(A)会逐渐稳定于事件A发生的概率P(A).
我们称频率的这个性质为频率的稳定性.
用频率fn(A)估计概率P(A)
二、新知学习(思考)
抛掷一枚质地均匀的硬币,“正面朝上”的概率为.
(样本点等可能)
(样本点不是等可能)
抛掷一枚图钉,“针尖朝上”的概率为多少?
二、新知学习(共同探究)
试验序号
试验总次数
出现“针尖朝上”的次数
出现“针尖朝上”的频率
1
55
35
0.636
2
55
34
0.618
3
55
33
0.600
合计
165
102
0.618
抛掷一枚图钉,“针尖朝上”的概率为多少?
三、例题讲解
例1
新生婴儿性别比是每100名女婴对应的男婴数.通过抽样调查得知,我国2014年,2015年出生的婴儿性别比分别为115.88和113.51.
(1)分别估计我国2014年和2015年男婴的出生率(新生儿中男婴的比率,精确到0.001);
分析:我国2014年,2015年出生的婴儿性别比分别为115.88和113.51.
2014年,女婴数:男婴数=100:115.88;
2015年,女婴数:男婴数=100:113.51.
三、例题讲解
解:2014年男婴出生的频率为
由此估计,我国2014年男婴出生率约为0.537,
2015年男婴的出生率约为0.532.
2015年男婴出生的频率为
三、例题讲解
例1
新生婴儿性别比是每100名女婴对应的男婴数.通过抽样调查得知,我国2014年,2015年出生的婴儿性别比分别为115.88和113.51.
(2)根据估计结果,你认为“生男孩和生女孩是等可能的”这个判断可靠吗?
男婴出生率
女婴出生率
2014年
0.537
0.463
2015年
0.532
0.468
因此,我们有理由怀疑“生男孩和生女孩是等可能的”的结论.
三、例题讲解
问题
在游戏过程中甲发现:玩了10次时,双方各胜5次;但玩到1000次时,自己才胜出300次,而乙却胜了700次.
据此,乙认为游戏公平,因为当游戏玩了10次时,甲、乙获胜的频率都为0.5;甲认为游戏不公平,因为当游戏玩到1000次时,甲获胜的频率为0.3,乙获胜的频率为0.7.
你更支持谁的结论?为什么?
游戏玩10次时,甲、乙获胜的频率都为0.5;
游戏玩到1000次时,甲获胜的频率为0.3,乙获胜的频率为0.7.
甲认为游戏不公平,乙认为游戏公平.
更愿意相信甲的判断
四、归纳
频率
概率
区别
本身是随机的观测值(试验值),在试验前无法确定,多数会随着试验的改变而变化,做同样次数的重复试验,得到的结果也会不同
本身是固定的理论值,与试验次数无关,只与事件自身的属性有关
联系
频率是概率的试验值,会随试验次数的增大逐渐稳定;概率是频率理论上的稳定值,在实际中可用频率估计概率
五、习题练习
课本P254
练习1、2
六、课堂小结
大量试验表明,在任何确定次数的随机试验中,一个随机事件A发生的频率具有随机性。
1.频率的稳定性
一般地,随着试验次数的增大,频率偏离概率的幅度会缩小,即事件发生的频率会逐渐稳定于事件发生的概率,我们称频率的这个性质为频率的稳定性.
2.频率稳定性的作用
可以用频率估计概率.
六、作业布置
完成相关习题
10.3
频率与概率
1、在问题情景中了解频率与概率的关系
2、理解频率与概率的关系,明确事件A发生的概率fn(A)与事件A发生的概率P(A)的区别与联系
3、了解蒙特卡洛方法,通过实例理解其步骤
学习目标
一、复习回顾
抛掷一枚质地均匀的硬币,“正面朝上”的概率为.
(样本点等可能)
(样本点不是等可能)
抛掷一枚图钉,“针尖朝上”的概率为多少?
实验者
掷币次数
出现“正面向上”的频数
频率
德·摩根
2048
1061
0.5181
蒲丰
4040
2048
0.5069
德·摩根
4092
2048
0.5005
费勒
10000
4979
0.4979
皮尔逊
12000
6019
0.5016
皮尔逊
24000
12012
0.5005
罗曼诺夫斯基
80640
39699
0.4923
二、新知学习(共同探究)
在重复试验中,频率的大小是否就决定了概率的大小呢?
频率与概率之间到底是一种怎样的关系呢?
二、新知学习(思考)
二、新知学习(共同探究)
重复做同时抛掷两枚质地均匀的硬币实验,设事件A=“一个正面朝上,一个反面朝上”,统计A出现的次数并计算频率,再与其概率进行比较,你能发现什么规律?
分析:把硬币正面朝上记为1,反面朝上记为0,
则这个试验的样本空间Ω=
,所以
二、新知学习(共同探究)
抛掷两枚质地均匀的硬币的试验:
(1)参与人员:42名高一学生;
(2)注意事项:每位同学都在相同的条件下同时抛掷两枚质地均匀的硬币.
二、新知学习(共同探究)
分步试验
第一步:每人重复做20次试验,记录事件A发生的次数,计算频率;
第三步:各组统计事件A发生的次数,计算事件A发生频率,然后汇总数据.
第二步:每7名同学为一组,相互比较试验结果,同时思考:每组中7名同学的结果一样吗?为什么会出现这样的情况?
二、新知学习(共同探究)
试验总次数
事件A发生的次数
事件A发生的频率
M同学
20
12
0.6
第1组
140
74
0.529
小组序号
试验总次数
事件A发生的次数
事件A发生的频率
1
140
74
0.529
2
140
51
0.364
3
140
78
0.557
4
140
81
0.579
5
140
59
0.421
6
140
80
0.571
合计
840
423
0.504
二、新知学习(思考)
(1)为什么各小组的试验结果不一样?
(2)随着试验次数的增加,事件A发生的频率有什么变化规律?
二、新知学习(共同探究)
试验总次数
事件A发生的次数
事件A发生的频率
M同学
20
12
0.6
第1组
140
74
0.529
小组序号
试验总次数
事件A发生的次数
事件A发生的频率
1
140
74
0.529
2
140
51
0.364
3
140
78
0.557
4
140
81
0.579
5
140
59
0.421
6
140
80
0.571
合计
840
423
0.504
二、新知学习(共同探究)
第一小组
小组成员
试验总次数
事件A发生的次数
事件A发生的频率
1
20
12
0.6
2
20
10
0.5
3
20
11
0.55
4
20
14
0.7
5
20
12
0.6
6
20
12
0.6
7
20
7
0.35
二、新知学习(共同探究)
第一小组
小组成员
试验总次数
事件A发生的次数
事件A发生的频率
1
20
12
0.6
2
20
10
0.5
3
20
11
0.55
4
20
14
0.7
5
20
12
0.6
6
20
12
0.6
7
20
7
0.35
二、新知学习(共同探究)
小组序号
试验总次数
事件A发生的次数
事件A发生的频率
1
140
74
0.529
2
140
51
0.364
3
140
78
0.557
4
140
81
0.579
5
140
59
0.421
6
140
80
0.571
合计
840
423
0.504
二、新知学习(共同探究)
小组序号
试验总次数
事件A发生的次数
事件A发生的频率
1
140
74
0.529
2
140
51
0.364
3
140
78
0.557
4
140
81
0.579
5
140
59
0.421
6
140
80
0.571
合计
840
423
0.504
二、新知学习(共同探究)
0.7-0.35=0.35
0.579-0.364=0.215
二、新知学习(共同探究)
小组序号
试验总次数
事件A发生的次数
事件A发生的频率
1
140
74
0.529
2
140
51
0.364
3
140
78
0.557
4
140
81
0.579
5
140
59
0.421
6
140
80
0.571
合计
840
423
0.504
试验次数为840次时,事件A发生的频率为0.504.
P(A)=0.5
二、新知学习(共同探究)
小组序号
试验总次数
事件A发生的次数
事件A发生的频率
1
140
74
0.529
2
140
51
0.364
3
140
78
0.557
4
140
81
0.579
5
140
59
0.421
6
140
80
0.571
合计
840
423
0.504
掷币次数
频率
2048
0.5181
4040
0.5069
4092
0.5005
10000
0.4979
12000
0.5016
24000
0.5005
80640
0.4923
0.504-0.
5=0.004
0.5181-0.
5=0.0181
二、新知学习(共同探究)
小组序号
试验总次数
事件A发生的次数
事件A发生的频率
1
140
74
0.529
2
140
51
0.364
3
140
78
0.557
4
140
81
0.579
5
140
59
0.421
6
140
80
0.571
合计
840
423
0.504
掷币次数
频率
2048
0.5181
4040
0.5069
4092
0.5005
10000
0.4979
12000
0.5016
24000
0.5005
80640
0.4923
只有1个:0.529
全部满足
事件A发生的频率记为
∣fn(A)-0.5∣≤0.05
二、新知学习(总结)
当试验次数较少时,用频率估计概率误差较小的可能性较小;
当试验次数足够多时,用频率估计概率误差较小的可能性大.
随着试验次数n的增大,频率偏离概率的幅度会缩小,即事件A发生的频率fn(A)会逐渐稳定于事件A发生的概率P(A).
我们称频率的这个性质为频率的稳定性.
用频率fn(A)估计概率P(A)
二、新知学习(思考)
抛掷一枚质地均匀的硬币,“正面朝上”的概率为.
(样本点等可能)
(样本点不是等可能)
抛掷一枚图钉,“针尖朝上”的概率为多少?
二、新知学习(共同探究)
试验序号
试验总次数
出现“针尖朝上”的次数
出现“针尖朝上”的频率
1
55
35
0.636
2
55
34
0.618
3
55
33
0.600
合计
165
102
0.618
抛掷一枚图钉,“针尖朝上”的概率为多少?
三、例题讲解
例1
新生婴儿性别比是每100名女婴对应的男婴数.通过抽样调查得知,我国2014年,2015年出生的婴儿性别比分别为115.88和113.51.
(1)分别估计我国2014年和2015年男婴的出生率(新生儿中男婴的比率,精确到0.001);
分析:我国2014年,2015年出生的婴儿性别比分别为115.88和113.51.
2014年,女婴数:男婴数=100:115.88;
2015年,女婴数:男婴数=100:113.51.
三、例题讲解
解:2014年男婴出生的频率为
由此估计,我国2014年男婴出生率约为0.537,
2015年男婴的出生率约为0.532.
2015年男婴出生的频率为
三、例题讲解
例1
新生婴儿性别比是每100名女婴对应的男婴数.通过抽样调查得知,我国2014年,2015年出生的婴儿性别比分别为115.88和113.51.
(2)根据估计结果,你认为“生男孩和生女孩是等可能的”这个判断可靠吗?
男婴出生率
女婴出生率
2014年
0.537
0.463
2015年
0.532
0.468
因此,我们有理由怀疑“生男孩和生女孩是等可能的”的结论.
三、例题讲解
问题
在游戏过程中甲发现:玩了10次时,双方各胜5次;但玩到1000次时,自己才胜出300次,而乙却胜了700次.
据此,乙认为游戏公平,因为当游戏玩了10次时,甲、乙获胜的频率都为0.5;甲认为游戏不公平,因为当游戏玩到1000次时,甲获胜的频率为0.3,乙获胜的频率为0.7.
你更支持谁的结论?为什么?
游戏玩10次时,甲、乙获胜的频率都为0.5;
游戏玩到1000次时,甲获胜的频率为0.3,乙获胜的频率为0.7.
甲认为游戏不公平,乙认为游戏公平.
更愿意相信甲的判断
四、归纳
频率
概率
区别
本身是随机的观测值(试验值),在试验前无法确定,多数会随着试验的改变而变化,做同样次数的重复试验,得到的结果也会不同
本身是固定的理论值,与试验次数无关,只与事件自身的属性有关
联系
频率是概率的试验值,会随试验次数的增大逐渐稳定;概率是频率理论上的稳定值,在实际中可用频率估计概率
五、习题练习
课本P254
练习1、2
六、课堂小结
大量试验表明,在任何确定次数的随机试验中,一个随机事件A发生的频率具有随机性。
1.频率的稳定性
一般地,随着试验次数的增大,频率偏离概率的幅度会缩小,即事件发生的频率会逐渐稳定于事件发生的概率,我们称频率的这个性质为频率的稳定性.
2.频率稳定性的作用
可以用频率估计概率.
六、作业布置
完成相关习题
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
