北师大版高中数学(必修2)1.8《面积公式和体积公式的简单应用》ppt课件
文档属性
| 名称 | 北师大版高中数学(必修2)1.8《面积公式和体积公式的简单应用》ppt课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 238.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-01 00:00:00 | ||
图片预览



文档简介
(共12张PPT)
引入
瞧,这么宏伟壮观的金字塔呀!
——你们能求出它的体积吗?
想知道吧?
让我们一起来学习今天的内容吧!
看,这不是不复存在的世贸大厦吗?
——这两个棱柱的体积怎么求?
取一摞书放在桌面上,将它如图那样改变一下形状,这时高度没有改变,每页纸的面积也没有改变,因而这摞书的体积与变形前相等吗?。
例如:
S1
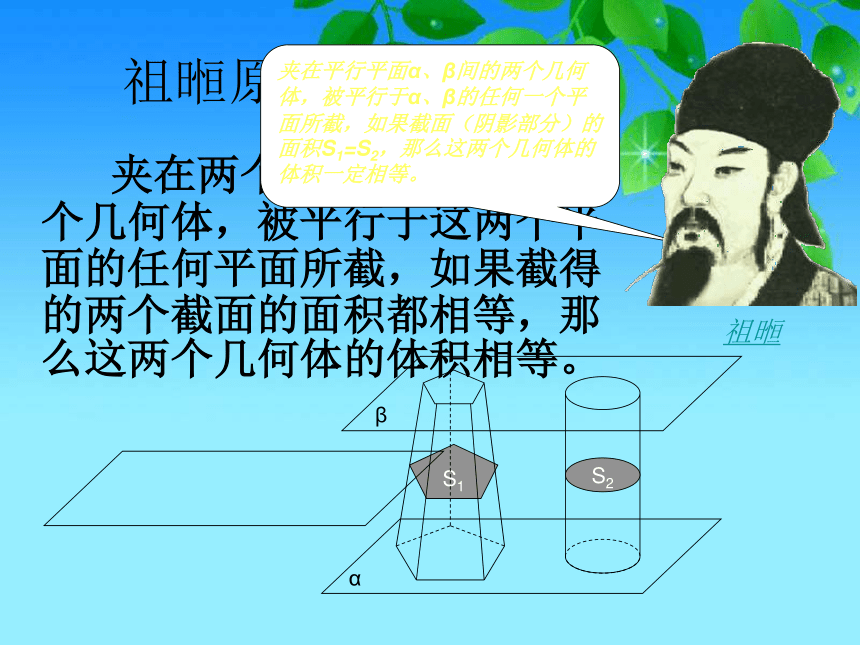
祖暅原理
夹在两个平行平面间的两个几何体,被平行于这两个平面的任何平面所截,如果截得的两个截面的面积都相等,那么这两个几何体的体积相等。
夹在平行平面α、β间的两个几何体,被平行于α、β的任何一个平面所截,如果截面(阴影部分)的面积S1=S2,那么这两个几何体的体积一定相等。
祖暅
S2
α
β
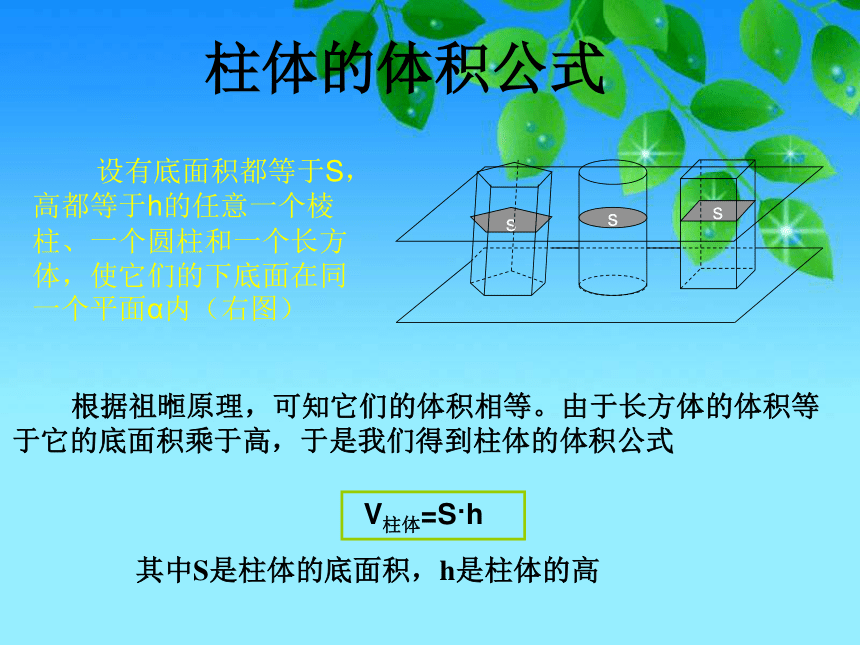
柱体的体积公式
设有底面积都等于S,高都等于h的任意一个棱柱、一个圆柱和一个长方体,使它们的下底面在同一个平面α内(右图)
其中S是柱体的底面积,h是柱体的高
s
s
s
根据祖暅原理,可知它们的体积相等。由于长方体的体积等
于它的底面积乘于高,于是我们得到柱体的体积公式
V柱体=S h
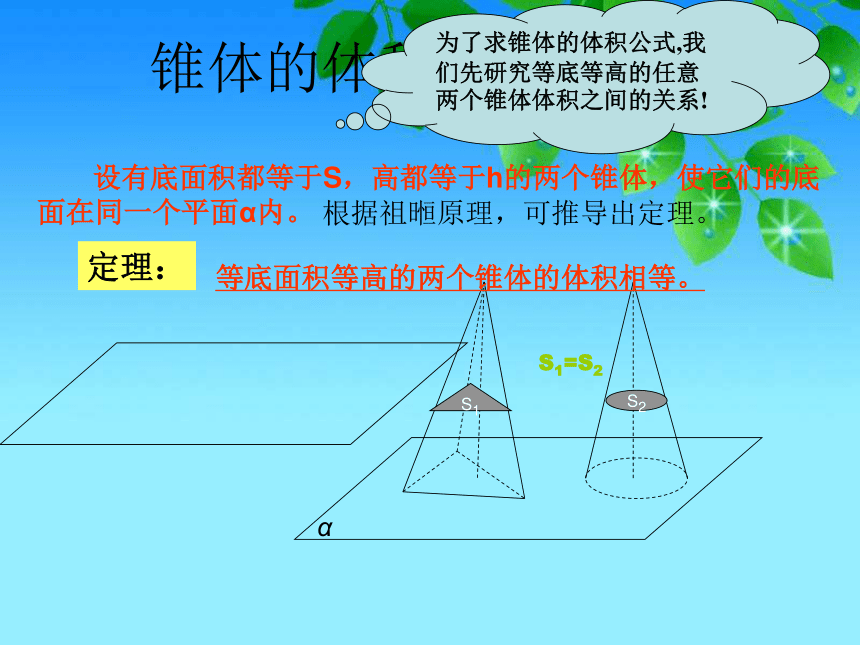
锥体的体积公式
设有底面积都等于S,高都等于h的两个锥体,使它们的底面在同一个平面α内。
α
为了求锥体的体积公式,我们先研究等底等高的任意两个锥体体积之间的关系!
根据祖暅原理,可推导出定理。
等底面积等高的两个锥体的体积相等。
S1
S2
S1=S2
定理:
将一个三棱柱按如图所示分解成三个三棱锥,那么这三个三棱锥的体积有什么关系?它们与三棱柱的体积有什么关系?
B
A
B1
C
C1
A1
B1
C
C1
A1
B
B1
C
A1
B
A
C
A1
对于一个任意的锥体,设它的底面积为S,高为h,那么它的体积应等于一个底面积为S,高为h的三棱锥的体积。
S
h
S
h
V三棱锥= S h
V圆锥= S h
如果一个锥体(棱锥、圆锥)的底面积是S,高是h,
那么它的体积是
V锥体= S h
定理:
例1:埃及的胡夫金字塔大约建于公元前2580年,其形状为正四棱锥,金字塔高约为146.6m底面边长约230.4m。问:这座金字塔的侧面积和体积各是多少?
A
C
B
解:六角螺帽毛坯的体积是一个正六棱柱的体积
与一个圆柱的体积的差.
V正六棱柱=1.732×122×6×10≈3.74×103(mm3)
V圆柱=3.14×52×10≈0.785×103(mm3)
毛坯的体积
V=3.74×103-0.785×103
≈2.96×103(mm3)=2.96(cm3)
∴ 5.8×103÷(7.8×2.96)≈2.5×102(个)
答:这堆毛坯约有250个。
O
N
P
例2:有一堆相同规格的六角螺毛坯共重5.8kg.已知底面六边形的边长是12mm,高是10mm,内孔直径10mm,问约有毛坯多少个(铁的比重是7.8g/cm3)
小结
知识点:
1、理解掌握 和 。
2、了解例题中有关的面积与其投影面积关系
方法点和思想点:
1、研究三棱柱与三棱锥体积公式关系时所用的 以及
其反面 的方法。
2、研究过程中体现出从 ,再从 的
思想方法。
教育点:
实际问题提醒把我们应注意联系实际生活。
锥体体积公式
柱体体积公式
割
补
一般到特殊
特殊到一般
作业:
引入
瞧,这么宏伟壮观的金字塔呀!
——你们能求出它的体积吗?
想知道吧?
让我们一起来学习今天的内容吧!
看,这不是不复存在的世贸大厦吗?
——这两个棱柱的体积怎么求?
取一摞书放在桌面上,将它如图那样改变一下形状,这时高度没有改变,每页纸的面积也没有改变,因而这摞书的体积与变形前相等吗?。
例如:
S1
祖暅原理
夹在两个平行平面间的两个几何体,被平行于这两个平面的任何平面所截,如果截得的两个截面的面积都相等,那么这两个几何体的体积相等。
夹在平行平面α、β间的两个几何体,被平行于α、β的任何一个平面所截,如果截面(阴影部分)的面积S1=S2,那么这两个几何体的体积一定相等。
祖暅
S2
α
β
柱体的体积公式
设有底面积都等于S,高都等于h的任意一个棱柱、一个圆柱和一个长方体,使它们的下底面在同一个平面α内(右图)
其中S是柱体的底面积,h是柱体的高
s
s
s
根据祖暅原理,可知它们的体积相等。由于长方体的体积等
于它的底面积乘于高,于是我们得到柱体的体积公式
V柱体=S h
锥体的体积公式
设有底面积都等于S,高都等于h的两个锥体,使它们的底面在同一个平面α内。
α
为了求锥体的体积公式,我们先研究等底等高的任意两个锥体体积之间的关系!
根据祖暅原理,可推导出定理。
等底面积等高的两个锥体的体积相等。
S1
S2
S1=S2
定理:
将一个三棱柱按如图所示分解成三个三棱锥,那么这三个三棱锥的体积有什么关系?它们与三棱柱的体积有什么关系?
B
A
B1
C
C1
A1
B1
C
C1
A1
B
B1
C
A1
B
A
C
A1
对于一个任意的锥体,设它的底面积为S,高为h,那么它的体积应等于一个底面积为S,高为h的三棱锥的体积。
S
h
S
h
V三棱锥= S h
V圆锥= S h
如果一个锥体(棱锥、圆锥)的底面积是S,高是h,
那么它的体积是
V锥体= S h
定理:
例1:埃及的胡夫金字塔大约建于公元前2580年,其形状为正四棱锥,金字塔高约为146.6m底面边长约230.4m。问:这座金字塔的侧面积和体积各是多少?
A
C
B
解:六角螺帽毛坯的体积是一个正六棱柱的体积
与一个圆柱的体积的差.
V正六棱柱=1.732×122×6×10≈3.74×103(mm3)
V圆柱=3.14×52×10≈0.785×103(mm3)
毛坯的体积
V=3.74×103-0.785×103
≈2.96×103(mm3)=2.96(cm3)
∴ 5.8×103÷(7.8×2.96)≈2.5×102(个)
答:这堆毛坯约有250个。
O
N
P
例2:有一堆相同规格的六角螺毛坯共重5.8kg.已知底面六边形的边长是12mm,高是10mm,内孔直径10mm,问约有毛坯多少个(铁的比重是7.8g/cm3)
小结
知识点:
1、理解掌握 和 。
2、了解例题中有关的面积与其投影面积关系
方法点和思想点:
1、研究三棱柱与三棱锥体积公式关系时所用的 以及
其反面 的方法。
2、研究过程中体现出从 ,再从 的
思想方法。
教育点:
实际问题提醒把我们应注意联系实际生活。
锥体体积公式
柱体体积公式
割
补
一般到特殊
特殊到一般
作业:
