北师大版高中数学(必修4)2.2《从位移的合成到向量的加法》(公开课)ppt课件
文档属性
| 名称 | 北师大版高中数学(必修4)2.2《从位移的合成到向量的加法》(公开课)ppt课件 |  | |
| 格式 | zip | ||
| 文件大小 | 412.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-01 11:05:03 | ||
图片预览




文档简介
(共19张PPT)
参赛者:李勇明(03号)
崇仁二中青年教师优质课竞赛
问题情景导入
V水
一条湍急的河流中一轮船以垂直对岸方向行驶,某游客自言自语:轮船怎么到达对岸的下游?
他百思不得其解!
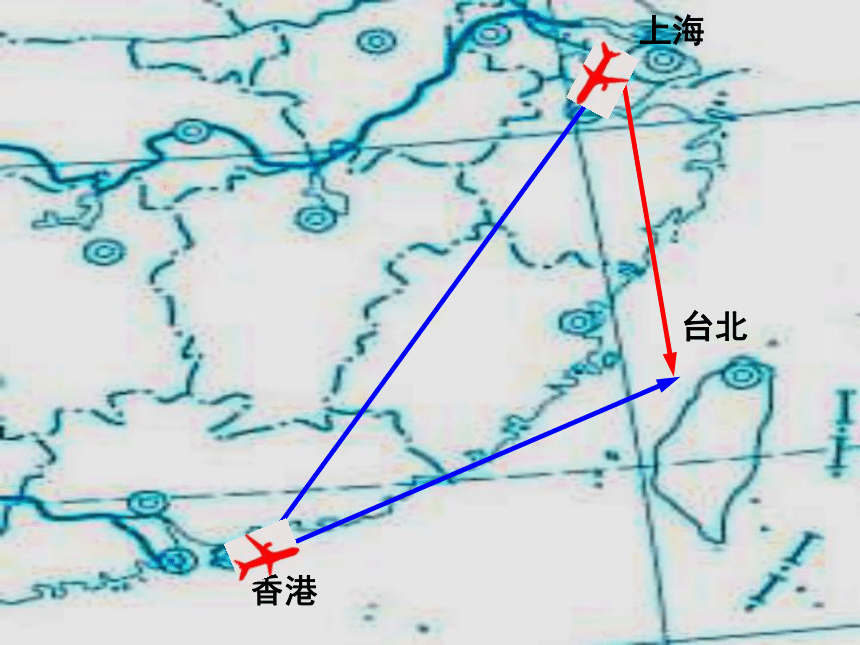
上海
香港
台北
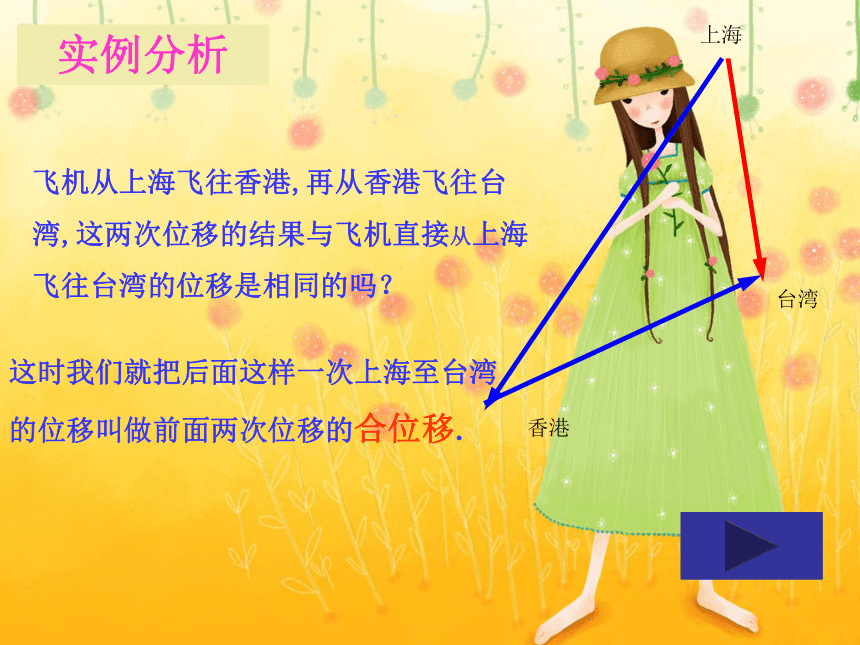
实例分析
飞机从上海飞往香港,再从香港飞往台湾,这两次位移的结果与飞机直接从上海飞往台湾的位移是相同的吗?
这时我们就把后面这样一次上海至台湾的位移叫做前面两次位移的合位移.
上海
香港
台湾
它的实际位移AB,可以看作水平运动的分位移AC与竖直向上运动的分位移AD的合位移.
A
B
C
D
由分位移求合位移,称为位移的合成
由上节课的学习我们知道位移是向量,因此位移合成就是向量的加法,那什么叫向量加法呢?它又符合哪些规律呢?这就是我们今天要探究的内容--------
§2从位移的合成到向量的加法 向量的加法(板书)
情景:在大型车间里,
一重物被天车从A处搬运到B处.
怎么来认识实际位移AB?
情景:在大型车间里,
一重物被天车从A处搬运到B处.
怎么来认识实际位移AB?
情景:在大型车间里,
一重物被天车从A处搬运到B处.
怎么来认识实际位移AB?
求两个向量和的运算叫向量的加法。
a
b
合作探究新知
既然向量的加法义可以类比位移的合成想一想,作两个向量的和是否也可以类比前面位移的合成呢?
探究1:
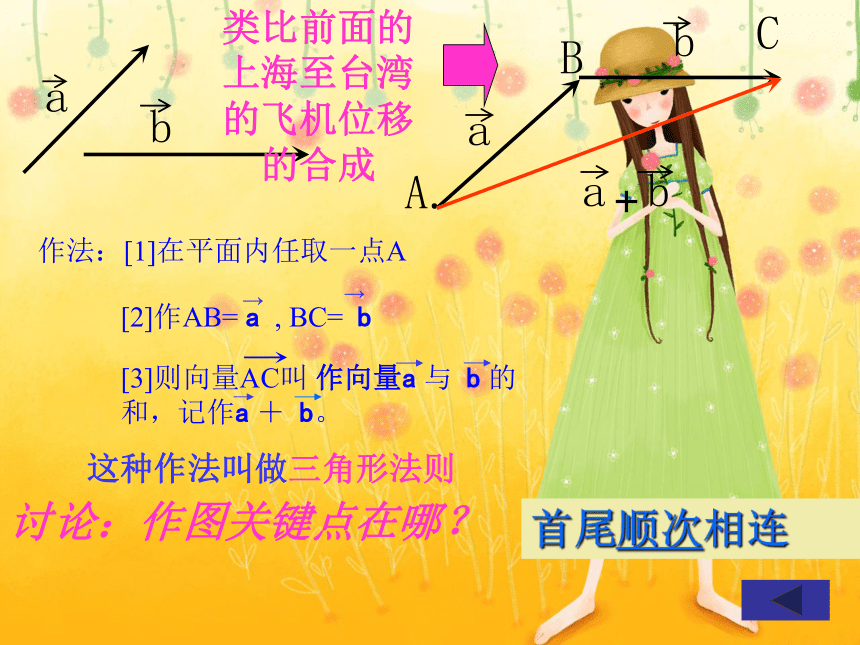
这种作法叫做三角形法则
a
b
A.
B
a
C
b
作法:[1]在平面内任取一点A
b
a
+
→
→
[2]作AB= a , BC= b
[3]则向量AC叫 作向量a 与 b 的和,记作a + b。
讨论:作图关键点在哪?
首尾顺次相连
类比前面的上海至台湾的飞机位移的合成
(1)同向
(2)反向
A
B
C
A
B
C
(3)规定:
问:
学以致用:P76练习第1题
这叫做向量加法的平行四边形法则。
a
b
A
a
B
b
D
C
a + b
讨论:作图关键点
平移为同一起点
作法:
作 AB= a, AD =b,以AB,AD为邻边
作平行四边形,则对角线向量 AC = a + b 。
及时反馈:P77练习第2题
类比天车从A处到B处的合位移为水平运动的分位移AC与竖直向上运动的分位移AD.
探究2:作两向量的加法还有没有其它的方法呢?
探究3:数的加法满足交换律与结合律,即对任意 a ,b∈R,有a+b=b+a, (a+b)+c=a+(b+c)
任意向量 的加法是否也满足交换律与结合律?
A1
A2
A3
探究4:能否将它推广至多个向量的求和?
A1
A2
A3
A4
A1A2+A2A3+A3A4=_______
A1A2+A2A3= _______
A1A3
A1A4
多边形法则:n个向量的和等于
折线起点到终点的向量
学以致用 (1) P77练习题第4 题
(2)变式 :求 =
0
A0A1+A1A2+...+An-1An=
A1An
思维方法归纳:
多个向量的和可以任意的组合
概念的形成
东
北
A
B
30
C
D
例1轮船从A港沿东偏北 30°方向行驶了40海里到达B处,再由B处沿正北方向行驶40海里到达C处.求此时轮船与A港的相对位置.
知识拓展与应用
例3 在小船过河时,小船沿垂直河岸方向行驶的速度为v1= km/h,河水流动的速度v2=2.0km/h
求小船过河实际航行速度的大小和方向.
例3 在小船过河时,小船沿垂直河岸方向行驶的速度为v1= km/h,河水流动的速度v2=2.0km/h
求小船过河实际航行速度的大小和方向.
A
B
D
例3 在小船过河时,小船沿垂直河岸方向行驶的速度为v1= km/h,河水流动的速度v2=2.0km/h
求小船过河实际航行速度的大小和方向.
变式(1):若要使小船沿垂直河岸方向到达对岸码头的实际速度的大小为了 km/h,
问:小船行驶的速度的大小和方向又该如何?
例3 在小船过河时,小船沿垂直河岸方向行驶的速度为v1= km/h,河水流动的速度v2=2.0km/h
求小船过河实际航行速度的大小和方向.
O
θ
C
A
B
F1
F2
例题改编(2):若小船在行驶过程中受到垂直河岸方向的牵引力为40N,水流的冲击力为30N,求小船在行驶中受到的合力。(学生练习)
50
求物理中的合速度、合位移、合力,可用向量的加法法来解决它。在解的过程中不但要求出它的大小,而且还要求出它们的方向。
思维方法提炼:
回顾与感悟
(一) 本节课的知识点深化
(二)方法的提炼
(2)向量加法的两个法则在物理中的运用。求物理中的合速度、合位移、合力,可用向量的加法法来解决它。在解的过程中不但要求出它的大小,而且还要求出它们的方向。
(3)对于变式(1)不用向量加法的平行四边形法则,那能否解决呢?
(1)课本P79 第 2、3题
(2)思考题:变式(1)放在三角形中如何求解?
分层作业
以竞赛促学习
以教研促提高
参赛者:李勇明(03号)
崇仁二中青年教师优质课竞赛
问题情景导入
V水
一条湍急的河流中一轮船以垂直对岸方向行驶,某游客自言自语:轮船怎么到达对岸的下游?
他百思不得其解!
上海
香港
台北
实例分析
飞机从上海飞往香港,再从香港飞往台湾,这两次位移的结果与飞机直接从上海飞往台湾的位移是相同的吗?
这时我们就把后面这样一次上海至台湾的位移叫做前面两次位移的合位移.
上海
香港
台湾
它的实际位移AB,可以看作水平运动的分位移AC与竖直向上运动的分位移AD的合位移.
A
B
C
D
由分位移求合位移,称为位移的合成
由上节课的学习我们知道位移是向量,因此位移合成就是向量的加法,那什么叫向量加法呢?它又符合哪些规律呢?这就是我们今天要探究的内容--------
§2从位移的合成到向量的加法 向量的加法(板书)
情景:在大型车间里,
一重物被天车从A处搬运到B处.
怎么来认识实际位移AB?
情景:在大型车间里,
一重物被天车从A处搬运到B处.
怎么来认识实际位移AB?
情景:在大型车间里,
一重物被天车从A处搬运到B处.
怎么来认识实际位移AB?
求两个向量和的运算叫向量的加法。
a
b
合作探究新知
既然向量的加法义可以类比位移的合成想一想,作两个向量的和是否也可以类比前面位移的合成呢?
探究1:
这种作法叫做三角形法则
a
b
A.
B
a
C
b
作法:[1]在平面内任取一点A
b
a
+
→
→
[2]作AB= a , BC= b
[3]则向量AC叫 作向量a 与 b 的和,记作a + b。
讨论:作图关键点在哪?
首尾顺次相连
类比前面的上海至台湾的飞机位移的合成
(1)同向
(2)反向
A
B
C
A
B
C
(3)规定:
问:
学以致用:P76练习第1题
这叫做向量加法的平行四边形法则。
a
b
A
a
B
b
D
C
a + b
讨论:作图关键点
平移为同一起点
作法:
作 AB= a, AD =b,以AB,AD为邻边
作平行四边形,则对角线向量 AC = a + b 。
及时反馈:P77练习第2题
类比天车从A处到B处的合位移为水平运动的分位移AC与竖直向上运动的分位移AD.
探究2:作两向量的加法还有没有其它的方法呢?
探究3:数的加法满足交换律与结合律,即对任意 a ,b∈R,有a+b=b+a, (a+b)+c=a+(b+c)
任意向量 的加法是否也满足交换律与结合律?
A1
A2
A3
探究4:能否将它推广至多个向量的求和?
A1
A2
A3
A4
A1A2+A2A3+A3A4=_______
A1A2+A2A3= _______
A1A3
A1A4
多边形法则:n个向量的和等于
折线起点到终点的向量
学以致用 (1) P77练习题第4 题
(2)变式 :求 =
0
A0A1+A1A2+...+An-1An=
A1An
思维方法归纳:
多个向量的和可以任意的组合
概念的形成
东
北
A
B
30
C
D
例1轮船从A港沿东偏北 30°方向行驶了40海里到达B处,再由B处沿正北方向行驶40海里到达C处.求此时轮船与A港的相对位置.
知识拓展与应用
例3 在小船过河时,小船沿垂直河岸方向行驶的速度为v1= km/h,河水流动的速度v2=2.0km/h
求小船过河实际航行速度的大小和方向.
例3 在小船过河时,小船沿垂直河岸方向行驶的速度为v1= km/h,河水流动的速度v2=2.0km/h
求小船过河实际航行速度的大小和方向.
A
B
D
例3 在小船过河时,小船沿垂直河岸方向行驶的速度为v1= km/h,河水流动的速度v2=2.0km/h
求小船过河实际航行速度的大小和方向.
变式(1):若要使小船沿垂直河岸方向到达对岸码头的实际速度的大小为了 km/h,
问:小船行驶的速度的大小和方向又该如何?
例3 在小船过河时,小船沿垂直河岸方向行驶的速度为v1= km/h,河水流动的速度v2=2.0km/h
求小船过河实际航行速度的大小和方向.
O
θ
C
A
B
F1
F2
例题改编(2):若小船在行驶过程中受到垂直河岸方向的牵引力为40N,水流的冲击力为30N,求小船在行驶中受到的合力。(学生练习)
50
求物理中的合速度、合位移、合力,可用向量的加法法来解决它。在解的过程中不但要求出它的大小,而且还要求出它们的方向。
思维方法提炼:
回顾与感悟
(一) 本节课的知识点深化
(二)方法的提炼
(2)向量加法的两个法则在物理中的运用。求物理中的合速度、合位移、合力,可用向量的加法法来解决它。在解的过程中不但要求出它的大小,而且还要求出它们的方向。
(3)对于变式(1)不用向量加法的平行四边形法则,那能否解决呢?
(1)课本P79 第 2、3题
(2)思考题:变式(1)放在三角形中如何求解?
分层作业
以竞赛促学习
以教研促提高
